دليل الخبراء لحساب إجهاد القص الانحناء وقوة العوارض

يوجد كل من عزم الانحناء وقوة القص على المقطع العرضي للعارضة التي تتعرض لقوة عرضية، مما ينتج عنه إجهاد عمودي وإجهاد قص على المقطع العرضي. سنناقش بعد ذلك إجهاد القص الانحناء للعديد من مقاطع العوارض الشائعة.

قسم مستطيل الشكل

قُطعت قطعة صغيرة طولها dx من العارضة تحت ثني القوة المستعرضة. لا يوجد حمل على العارضة وقوى القص على جانبي القطعة متساوية ولكن في اتجاهين متعاكسين. يكون عزم الانحناء عند القطعة اليمنى أكبر من عزم الانحناء عند القطعة اليسرى، مما يؤدي إلى اختلاف الإجهاد العمودي على القطعتين.

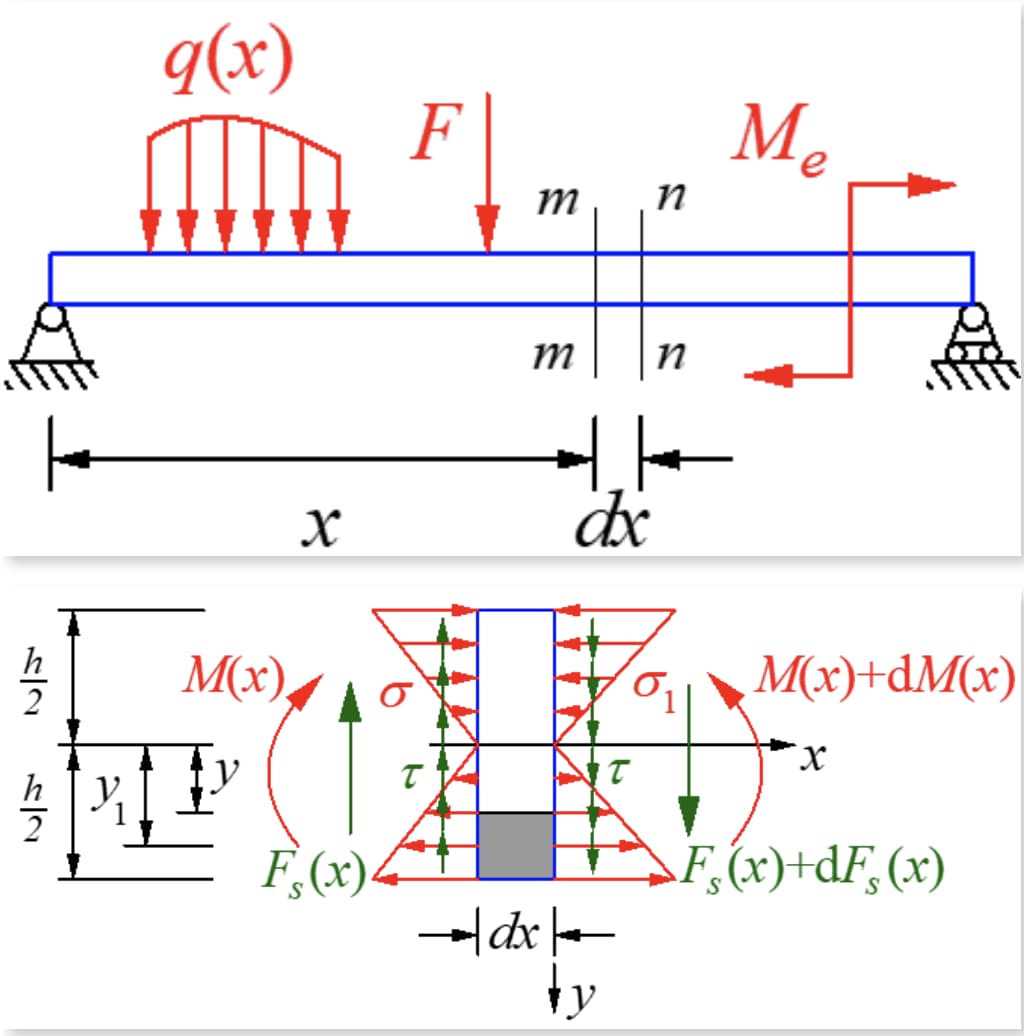
بالنسبة للمقطع المستطيل الضيق، يكون إجهاد القص مماسًا للحد الفاصل على جانبي العارضة بسبب عدم وجود إجهاد قص على الجانب. هذا يعني أنه نظرًا لأن العارضة منحنية بشكل متماثل وموازية للحد الفاصل، يجب أن يكون إجهاد القص على المحور y لمحور التماثل في الاتجاه y ويتغير قليلاً على طول اتجاه العرض.

لذلك، يتم وضع الافتراضات التالية حول قانون توزيع إجهاد القص على المقطع العرضي:

• اتجاه إجهاد القص عند كل نقطة على المقطع العرضي موازٍ لقوة القص;
• يتم توزيع إجهاد القص بالتساوي على طول عرض المقطع، أي أن إجهاد القص عند كل نقطة على الخط الأفقي الموازي للمحور المحايد يكون متساويًا.

عندما تكون نسبة الارتفاع إلى العرض للمقطع أكبر من 2، يكون الحل القائم على الافتراض أعلاه دقيقًا بما فيه الكفاية مقارنة بالحل الدقيق من النظرية المرنة.

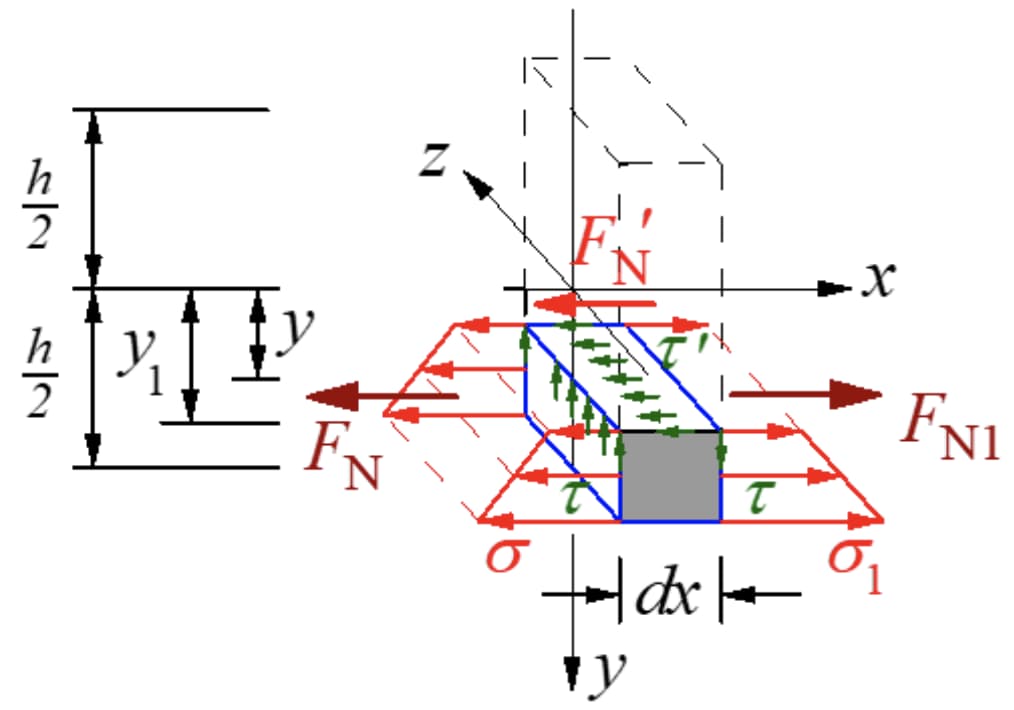
وفقًا لنظرية تبادلية إجهاد القص، يجب أن يكون إجهاد القص مساويًا لحجم المقطع العرضي على المقطع الطولي العمودي على المقطع العرضي. اقطع قطعة متناهية الصغر على طول المستوى الطولي بحيث يكون محور العزم المحايد بعيدًا عن y، وخذ العنصر المتناهية الصغر على الجانب السفلي من المستوى الطولي. تكون القوى كما هو موضح في الشكل أدناه.

القوة المحصلة للإجهاد العمودي على الجزء الأيسر هي:

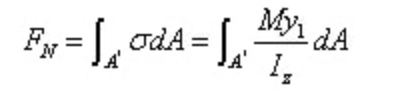
القوة المحصلة للإجهاد العمودي على الجزء الأيمن هي:：

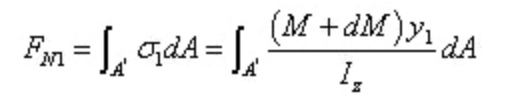
من الواضح أن المحصولين مختلفان في الحجم. لا بد من وجود قوة على طول الاتجاه المحوري على المقطع الطولي للحفاظ على توازن القطعة الصغرى. هذه القوة هي نتيجة إجهاد القص، مما يؤكد وجود إجهاد القص على المقطع الطولي.

بما أن dx مقدار صغير، فليكن إجهاد القص على المستوى الطولي موزعًا بالتساوي ：

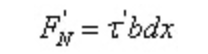
وفقًا لشروط التوازن ：

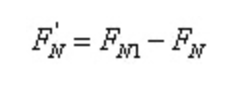
هذا هو,

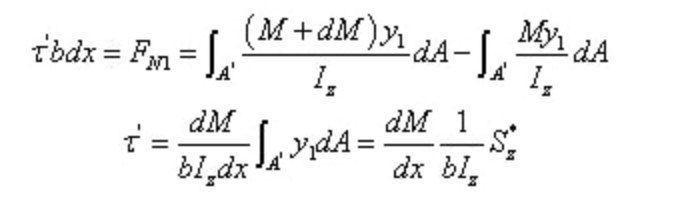
من بين,

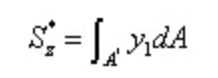
من نظرية مقلوب إجهاد القص والعلاقة التفاضلية بين قوة القص وعزم الانحناء:

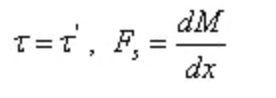
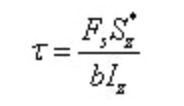
منها

• b هو عرض الخط الأفقي مع المحور المحايد للعزم y على المقطع، وهو ثابت للمقاطع المستطيلة;
• I_z هو عزم القصور الذاتي للمحور المحايد للمقطع العرضي بأكمله;
• S_z* هو العزم السكوني للمساحة خارج الخط الأفقي الذي يكون محوره المحايد y على المقطع العرضي إلى المحور المحايد;
• F_S هي قوة القص المؤثرة على المقطع العرضي.

من بين,

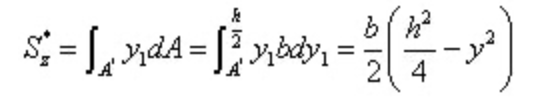
الاستبدال في معادلة حساب إجهاد القص

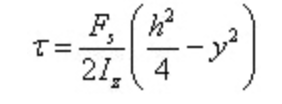
إجهاد القص هو قطع مكافئ موزع على طول ارتفاع المقطع.

عندما تكون y=0، يوجد أقصى إجهاد قص على المقطع عند المحور المحايد

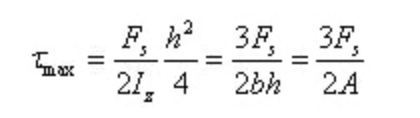
الإجهاد الزاوي هو

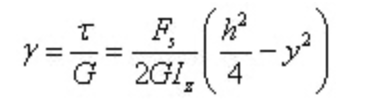
يمكن ملاحظة أن الإجهاد الزاوي موزع بشكل مكافئ أيضًا على طول ارتفاع المقطع.

في هذا الوقت، يظهر شكل التواء المقطع العرضي عند انحناء القوة العرضية في الشكل أدناه، وهو ما يؤكد أن تشوه انحناء القوة العرضية لا يتوافق مع افتراض المستوى.

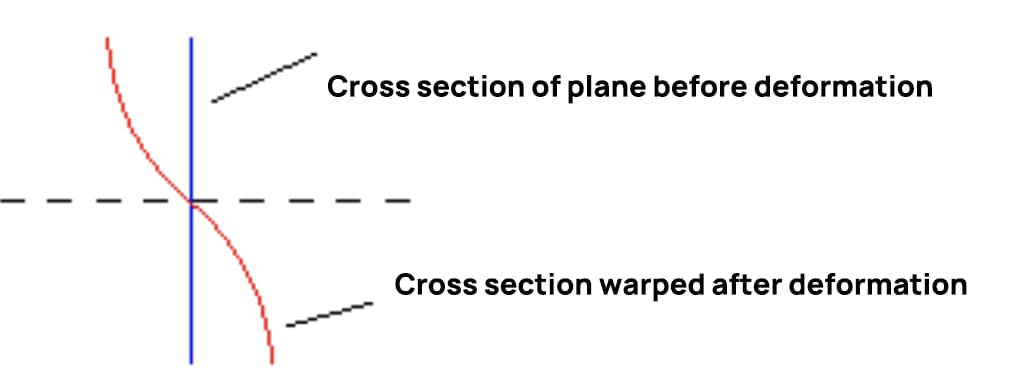
عندما تظل قوة القص ثابتة، يكون إجهاد القص على المقاطع العرضية المتتالية متساويًا، وتكون درجة الالتواء متساوية أيضًا. لا يتغيّر طول الألياف الطولية بسبب التواء المقطع، لذلك لن ينتج عنه إجهاد عمودي إضافي. إذا تغيرت قوة القص مع موضع المقطع، فإن درجة الالتواء على مقطعين متتاليين ستكون مختلفة، مما يؤدي إلى إجهاد عمودي إضافي على المقطع.

بالنسبة للمقاطع المتماثلة ذات الأشكال الأخرى، يمكن اشتقاق حل إجهاد القص التقريبي باستخدام الطريقة المذكورة أعلاه.

بالنسبة للمقطع المستطيل، في معادلة حساب الإجهاد، يكون عرض المقطع (ب) ثابتًا، ويكون العزم الاستاتيكي لنصف مساحة المقطع العرضي على جانب واحد من المحور المحايد إلى المحور المحايد هو الأكبر. ونتيجة لذلك، يكون إجهاد القص عند كل نقطة على المحور المحايد هو الأكبر.

بالنسبة للمقاطع المتماثلة ذات الأشكال الأخرى، عادةً ما يقع أقصى إجهاد قص على المقطع العرضي عند نقاط مختلفة على المحور المحايد، باستثناء المقاطع ذات العرض المتزايد بشكل كبير عند المحور المحايد (مثل المقاطع العرضية) أو بعض المقاطع ذات العرض المتغير (مثل المقاطع المثلثية المتساوية الساقين).

لذلك، بالنسبة للعوارض ذات الشكل I، والحلقية، والدائرية المقطع، ستتم مناقشة إجهاد القص الأقصى عند كل نقطة على المحور المحايد بشكل أساسي أدناه.

القسم الدائري

يكون إجهاد القص عند كل نقطة على حافة مقطع دائري مماسًا للمحيط، وفقًا لنظرية المقلوب لإجهاد القص. عند كل نقطة من محور التماثل، يجب أن يكون إجهاد القص في الاتجاه y. يمكن افتراض أن توزيع إجهاد القص يتقارب عند نقطة على محور التماثل لكل نقطة على طول العرض y من المحور المحايد، وتكون مركبات إجهاد القص على طول الاتجاه Y عند كل نقطة على طول العرض متساوية.

يظل أقصى إجهاد قص للمقطع الدائري على المحور المحايد، ويكون اتجاهه موازيًا للقوة الخارجية، بنفس القيمة عند كل نقطة على المحور المحايد.

الحد الأقصى لإجهاد القص هو

مقطع عرضي على شكل I

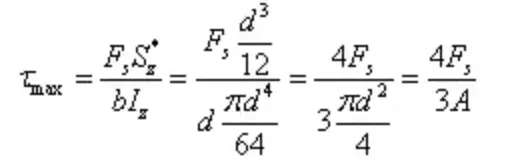
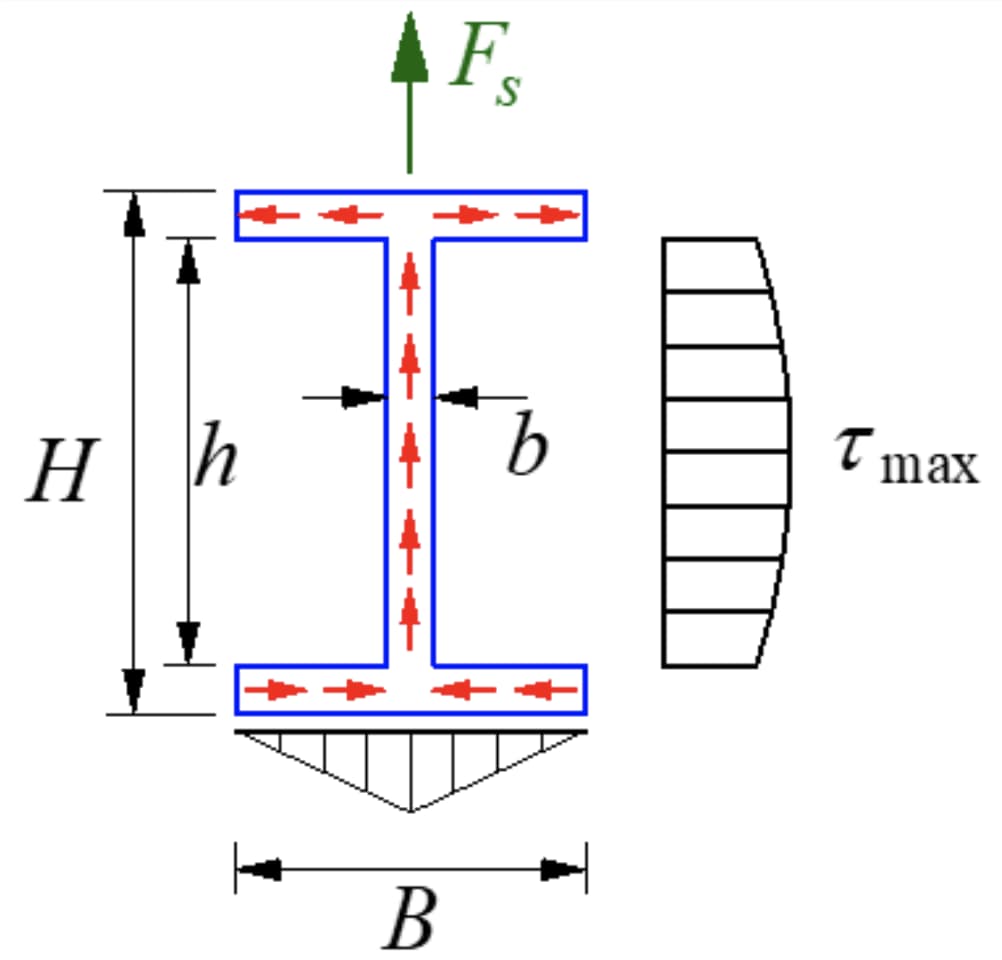
المقطع على شكل حرف I عبارة عن مقطع مفتوح رقيق الجدران مع توزيع إجهاد كما هو موضح في الشكل. يتساوى مقدار إجهاد القص على طول سُمك الجدار، وهو ما يُعرف بتدفق إجهاد القص، ويتدفق في اتجاه القص.

يكون مكوِّن إجهاد القص الموازي للمحور y على الحافة ثانويًا ولا يُذكر، مع التركيز بشكل رئيسي على المكوِّن الموازي للجانب الطويل من الحافة. يتوزع إجهاد القص على الشبكة توزيعًا مكافئًا، مع توضيح حجمه في الشكل.

يكون أقصى إجهاد قص عند المحور المحايد.

في حالة فولاذ على شكل Iإجهاد القص الأقصى:

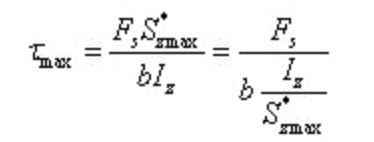
حيث، b هو سُمك الشبكة، وI_z/s*_زماكس يمكن الحصول عليها بالرجوع إلى جدول الفولاذ الجانبي.

إذا كان مقطعًا على شكل حرف I مكوَّنًا من ثلاثة مستطيلات طويلة وضيقة، فيمكن الحصول على أقصى وأدنى إجهادات القص على الشبكة على النحو التالي:

من المعادلتين المذكورتين أعلاه، يمكن ملاحظة أن عرض الشبكة أصغر بكثير من عرض الحافة، وبالتالي فإن أقصى إجهاد قص على الشبكة لا يختلف كثيرًا عن أدنى إجهاد قص.

لذلك، يمكن اعتبار أن إجهاد القص على الشبكة موزع بالتساوي تقريبًا.

يمثل إجهاد القص الناتج على الوصلة 95-97% من إجمالي قوة القص، وتتحمل الوصلة معظم قوة القص على المقطع العرضي.

بما أن الشبكة تتحمل كل قوة القص تقريبًا على المقطع، وبما أن إجهاد القص على الشبكة موزع بالتساوي تقريبًا، يمكن حساب أقصى إجهاد قص تقريبًا بقسمة قوة القص على مساحة المقطع العرضي للقطب البطني:

وفي الوقت نفسه، فإن منطقة شعاع I-شعاع تكون الحافة أبعد ما تكون عن المحور المحايد، ويكون الإجهاد العمودي عند كل نقطة كبيرًا نسبيًا، وبالتالي فإن الحافة تتحمل معظم عزم الانحناء على المقطع.

قسم حلقي رقيق الجدار رقيق الجدار

سمك المقطع الحلقي ذي الجدران الرقيقة هو d، ومتوسط نصف قطر الحلقة هو r، وسمكه أقل بكثير من متوسط نصف القطر، لذا يمكن افتراض أن

يتساوى إجهاد القص على المقطع العرضي على طول سُمك الجدار;

يكون اتجاه إجهاد القص مماسًا للخط المركزي للمقطع، ويكون اتجاه تدفق إجهاد القص على طول اتجاه القص.

يقع أقصى إجهاد قص على المحور المحايد:

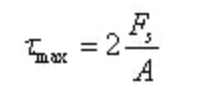
حيث، A هي مساحة المقطع الحلقي.

حالة قوة العارضة

حالة قوة إجهاد الانحناء العادي:

بالنسبة للمقاطع المحايدة غير المتماثلة، يتساوى أقصى إجهاد عمودي شد وأقصى إجهاد عمودي انضغاطي.

المواد البلاستيكية شائعة الاستخدام، وشروط قوتها:

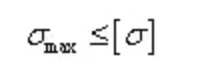
أما بالنسبة للمقطع ذي المحور المحايد غير المتماثل، فإن أقصى إجهاد شد عمودي وأقصى إجهاد ضغط عمودي غير متساويين.

المواد الهشة شائعة الاستخدام، وشروط قوتها:

شرط قوة إجهاد القص الانحناء هو:

تدابير تحسين قوة ثني العوارض الخشبية

الإجهاد العمودي الانحناء هو العامل الرئيسي الذي يتحكم في العارضة.

ولذلك، غالبًا ما تكون حالة قوة الانحناء للإجهاد العادي هي الأساس الرئيسي لتصميم العوارض.

من حالة القوة، لتحسين قدرة تحمل العارضة، يجب مراعاة جانبين:

فمن ناحية، يجب أن يكون إجهاد العارضة مرتبًا بشكل معقول لتقليل الحد الأقصى لعزم الانحناء;

من ناحية أخرى، يتم اعتماد شكل مقطع معقول لتحسين معامل مقطع الانحناء للمقطع والاستفادة الكاملة من خصائص المادة.

1. ترتيب إجهاد العارضة بشكل معقول

تحسين حالة إجهاد العارضة ومحاولة تقليل الحد الأقصى لعزم الانحناء في العارضة.

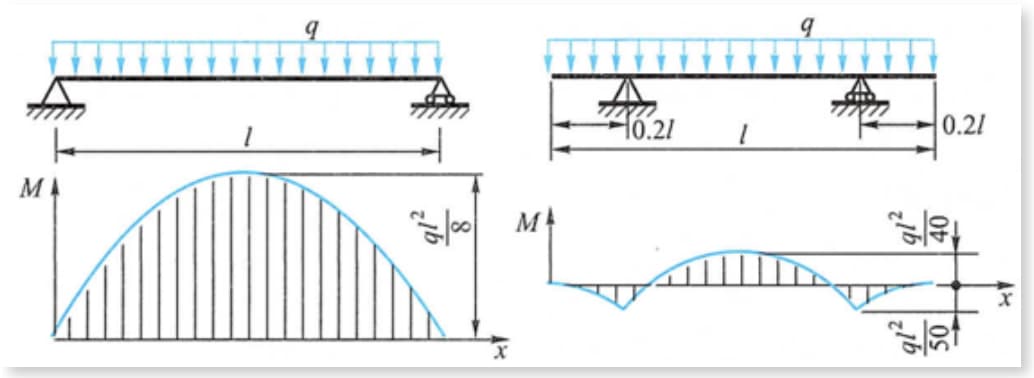
كما هو موضح في الشكل، ينخفض عزم الانحناء الأقصى على العارضة تحت الحمل المنتظم بشكل كبير عندما يتم تحريك الدعامة إلى الداخل لمسافة معينة من مواضع طرفي العارضة.

على سبيل المثال، يمكن أن تحقق العارضة والحاوية الأسطوانية للرافعة الجسرية، التي تتحرك نقطة دعمها قليلاً إلى المنتصف، تأثير تقليل أقصى عزم انحناء.

2. جزء معقول من العارضة

كلما زاد معامل مقطع الانثناء، قلّ الإجهاد وزادت قدرة تحمل العارضة.

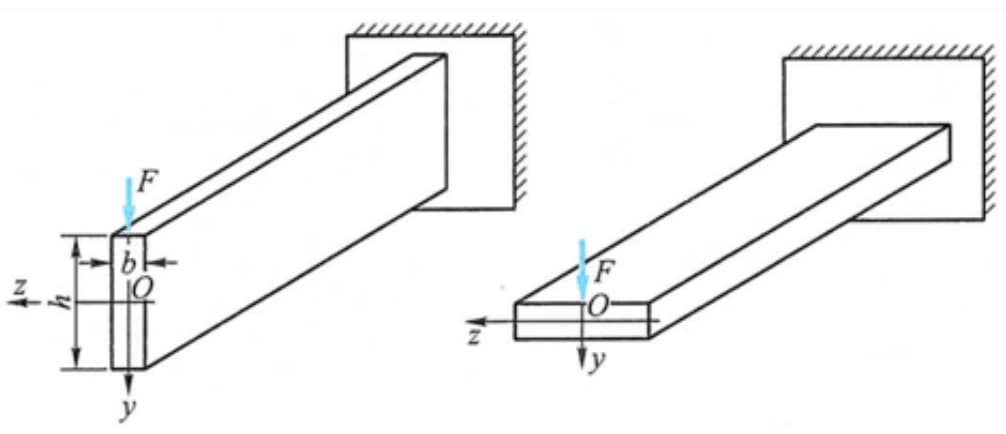
على سبيل المثال، عندما يتم تحميل العارضة في الاتجاه العمودي، يكون معامل مقطع الانحناء أكبر عندما يتم وضع المقطع عموديًا، لذلك من المنطقي وضعه عموديًا أكثر من وضعه أفقيًا.

أثناء تحسين معامل مقطع الانحناء للقسم، نأمل أيضًا في استخدام مواد أقل لتحقيق اقتصاد أفضل.

لذلك، تُستخدم نسبة معامل مقطع الانحناء إلى مساحة المقطع بشكل عام لقياس مدى عقلانية تصميم المقطع.

في ظل نفس مساحة المقطع العرضي، يكون المقطع المستطيل (الارتفاع أكبر من العرض) أكثر معقولية من المقطع الدائري، في حين أن المقطع على شكل حرف I أو المقطع الصندوقي أكثر معقولية من المقطع المستطيل.

لذلك، من أجل الاستفادة الكاملة من المواد، يجب وضع المواد بعيدًا عن المحور المحايد قدر الإمكان.

عند مناقشة الشكل المعقول للقسم، فإن الخواص الميكانيكية من المادة يجب أن تؤخذ في الاعتبار أيضًا.

يجب أن تعتمد المواد التي لها نفس قوة الشد والضغط (مثل الفولاذ منخفض الكربون) على مقاطع محايدة متماثلة، مثل المقاطع الدائرية والمستطيلة والشكل I والصندوقية وغيرها.

وبهذه الطريقة، يمكن أن يتساوى أقصى إجهاد شد وأقصى إجهاد انضغاطي عند الحافتين العلوية والسفلية للمقطع.

بالنسبة للمواد ذات قوة الشد والضغط غير المتكافئة (مثل الحديد الزهر والأسمنت وغيرها)، يجب اعتماد شكل المقطع مع المحور المحايد المائل إلى جانب الشد.

مفهوم الحزمة المتساوية القوة

العوارض التي تمت مناقشتها أعلاه جميعها ذات مقاطع متساوية، ومعامل مقطع الانحناء ثابت، ولكن بشكل عام، يتغير عزم الانحناء لكل مقطع من العارضة مع موضع المقطع.

يجب أن يتم تصميم مقطع العارضة المستقيمة المتساوية وفقًا لعزم الانحناء الأقصى، وأن يكون الحد الأقصى للإجهاد قريبًا من الإجهاد المسموح به.

يكون عزم الانحناء على المقاطع الأخرى صغيرًا، وبالتالي يكون الإجهاد صغيرًا، ولا يتم استخدام المادة بالكامل.

من أجل توفير المواد وتقليل الوزن الذاتي، يمكن تغيير حجم المقطع بحيث يتغير معامل مقطع الانحناء مع عزم الانحناء.

يستخدم مقطع أكبر حيث يكون عزم الانحناء أكبر، بينما يستخدم مقطع أصغر حيث يكون عزم الانحناء أصغر.

يُطلق على هذا النوع من الحزم التي يتغير مقطعها على طول المحور اسم الحزم المتغيرة المقطع.

إذا كان الحد الأقصى للإجهاد العمودي على كل مقطع عرضي في العارضة متغيرة المقطع العرضي متساويًا ومساويًا للإجهاد المسموح به، فإنها تسمى عارضة متساوية القوة.