Have you ever wondered how power is transmitted between machines? Belt drives are a simple yet ingenious solution that has revolutionized mechanical engineering. In this blog post, we’ll explore the fascinating world of belt drives, from their basic principles to their diverse applications. Join us as we unravel the mysteries behind this essential component of modern machinery and discover how it continues to shape our world today.
A belt drive is a mechanical power transmission system that transfers rotational motion and torque from a driving shaft to one or more driven shafts using a continuous, flexible belt. This system is particularly effective when the drive and driven components are spatially separated, allowing for efficient power transfer over considerable distances.
Belt drives consist of several key components:
Compared to other mechanical transmissions, belt drives offer several advantages:
However, belt drives also have limitations:
The belt drive system is a fundamental power transmission mechanism comprising several key components: a drive pulley, a driven pulley, a transmission belt tightly fitted over both pulleys, and a supporting machine frame, as illustrated in figure 8-1. This arrangement facilitates the transfer of mechanical energy from one rotating shaft to another through frictional forces.
The drive pulley, typically connected to a power source such as an electric motor or engine, initiates the system’s motion. As it rotates, the pulley’s surface friction engages the transmission belt, causing it to move. This movement is then transferred to the driven pulley, which is mounted on the shaft of the machine or device requiring power.
The efficiency and performance of a belt drive system depend on several factors:
Belt drives offer advantages such as shock absorption, noise reduction, and the ability to transmit power over considerable distances. However, they may require periodic maintenance and replacement due to wear and stretch over time.
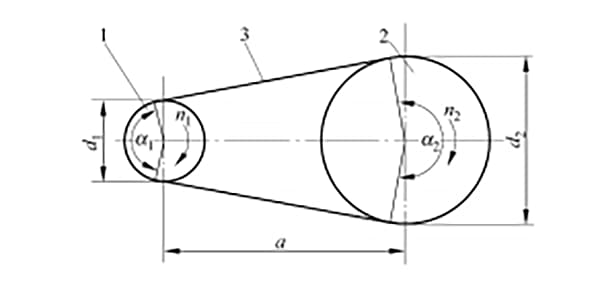
1- Driving pulley
2- Driven pulley
3- Drive belt
Belt drives can be classified into frictional and meshing types according to their driving principles. This article primarily discusses issues related to frictional belt drives.
2.1. Frictional belt drives operate by transmitting motion and power through the frictional force generated between the drive belt, which fits tightly on the pulley, and the pulley’s contact surface. Based on the cross-sectional shape of the drive belt, they can further be divided into flat belts, V-belts, multi-wedge belts, and round belts.
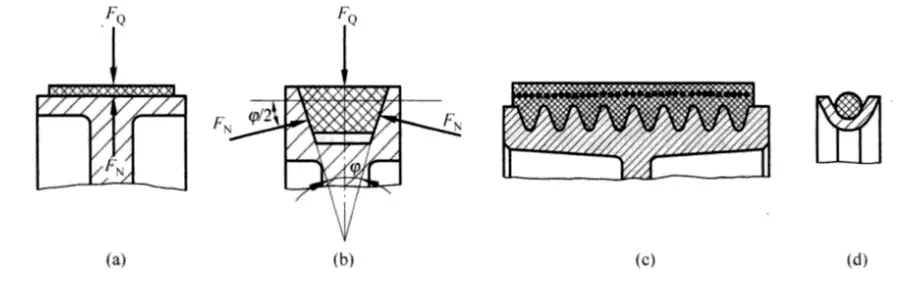
2.1.1 The cross-section of a flat belt is rectangular, and its inner surface that comes in contact with the pulley is the working face. It is primarily used for long-distance transmission between two parallel shafts rotating in the same direction.
2.1.2 The cross-section of a V-belt is trapezoidal, with the two sides contacting the pulley groove serving as the working surfaces. The pulley groove is also trapezoidal. Force analysis on the wedge surface reveals that under equal tension and friction coefficient conditions, the friction force generated by the V-belt is greater than that of the flat belt.
Therefore, the V-belt has a stronger transmission capacity and a more compact structure, making it widely used in mechanical transmission. Depending on their relative width and height, V-belts can be further divided into types such as regular V-belts, narrow V-belts, wide V-belts, automobile V-belts, cogged V-belts, and high-angle V-belts. Currently, regular V-belts are the most widely used.
2.1.3 The multi-wedge belt, a hybrid of the flat belt and multiple V-belts, combines the advantages of both and is often used in large power transmission systems where a compact structure is required.
2.1.4 The cross-section of a round belt is circular and is used only in low-speed, low-power transmissions such as sewing machines and instruments.
2.2 Meshing belt drive transmits motion and power by meshing the teeth of the belt with those on the pulley. The synchronous belt drive, as shown in Figure 8-3, is a typical example.
In addition to retaining the advantages of friction belt transmission, synchronous belts also offer high power transmission, precise gear ratios, and are often used in situations requiring smooth transmission and high precision, such as in tape recorders, food mixers, CNC machine tools, and textile machinery. The cross-section of a synchronous belt is rectangular, with the inner surface of the belt toothed.
Unlike the structure of a belt in friction drive, the strength layer of a synchronous belt is mostly composed of steel wire ropes, which results in less deformation under load. The edge of the synchronous pulley is also manufactured with an involute tooth shape corresponding to the inner surface of the belt, produced using a generating process by involute gear cutting tools. Therefore, the dimensions of the pulley teeth depend on the size of the cutting tools used.
Belt drives exhibit excellent elasticity, enabling them to effectively buffer and absorb vibrations, ensuring smooth power transmission with minimal noise generation. During overload conditions, controlled slippage between the belt and pulley serves as a protective mechanism, preventing potential damage to other drivetrain components. The simplicity of belt transmission systems facilitates ease of manufacturing, installation, and maintenance, resulting in cost-effective power transfer solutions.
In operation, transmission belts may experience elastic slip, which can lead to slight variations in the transmission ratio. This phenomenon, while generally manageable, prevents the maintenance of a strictly constant speed ratio. Belt drives typically feature larger overall dimensions compared to other power transmission methods, which can result in slightly lower transmission efficiencies. Consequently, belt transmission systems are most commonly employed for power transfer applications ≤ 50kW, with optimal belt speeds ranging from 5 to 25 m/s. The recommended transmission ratio for efficient operation should not exceed 5:1. Under proper design and maintenance conditions, belt drive systems can achieve efficiencies between 92% and 97%.
Belt drives operate under dynamic conditions where elastic deformation plays a crucial role in power transmission and system reliability. The drive belt, composed of elastomeric materials and reinforcing fibers, exhibits viscoelastic behavior under load. As tension is applied, the belt undergoes elastic stretching, with the magnitude of deformation directly proportional to the applied tension force.
During operation, a tension differential exists between the tight side (F1) and the slack side (F2) of the belt, with F1 > F2. This tension imbalance results in non-uniform elastic stretching along the belt’s length. The tight side experiences greater elongation due to higher tensile stress, while the slack side exhibits comparatively less stretch. This differential stretching is fundamental to the belt’s ability to transmit power efficiently.
The elastic nature of the belt also contributes to two critical phenomena:
Elastic slippage is an intrinsic phenomenon in belt drive operations, occurring inevitably during the working cycle of the drive belt. This complex behavior arises from the elastic properties of the belt material and the varying tension forces experienced along the belt path.
As the tight side of the drive belt engages with the driving pulley at point A, the belt velocity (v) initially matches the circumferential velocity (v1) of pulley 1. However, as pulley 1 rotates from point A to point B, the tension force in the belt gradually decreases from F1 to F2, resulting in a corresponding reduction in elastic elongation. This progressive shortening of the belt causes a minute rearward relative slippage along the pulley face, leading to a belt velocity (v) that becomes slightly less than the circumferential velocity (v1) of pulley 1.
Conversely, as the belt interfaces with the driven pulley 2 from entry point C to exit point D, friction-induced forces cause the belt tension to increase from F2 back to F1. This tension increase leads to a gradual elongation of the belt. Consequently, a small forward relative slippage occurs on the surface of pulley 2, resulting in a belt velocity (v) that marginally exceeds the angular velocity (v2) of pulley 2. This differential slippage due to the elastic deformation of the drive belt is termed elastic slippage.
The implications of elastic slippage are significant:
To mitigate the effects of elastic slippage, engineers may employ strategies such as optimizing belt tension, selecting appropriate belt materials with reduced elasticity, or implementing active tensioning systems in critical applications. Understanding and accounting for elastic slippage is crucial in the design and maintenance of efficient and reliable belt drive systems across various industrial applications.
The primary failure modes during the operation of a belt drive system are belt slippage on the pulley, accelerated belt wear, and fatigue-induced failure. Each of these modes can significantly impact system performance and reliability:
Additionally, less common but equally critical failure modes include:
2.1 Slippage
Belt drives operate on friction. When the initial tension force F₀ is constant, if the effective circumferential force F exceeds the limit friction force between the belt and the wheel surface, the belt will experience obvious, full-scale sliding on the wheel surface, a phenomenon known as slippage.
When the belt exhibits slippage, although the driving pulley continues to rotate, both the driven pulley and the belt incur substantial speed loss, or even come to a complete halt. Slippage is a detrimental phenomenon as it causes drive failure and exacerbates belt wear. During normal operation, slippage should be avoided.
Elastic sliding and slippage are two distinctly different concepts. Their differences are outlined in Table 8-1.
Table 8-1 Differences between elastic sliding and slipping
| Item | Elastic sliding | Slipping |
| Phenomenon | The sliding of the local belt on the local wheel surface | Relative sliding occurs between the belt and the wheel surface on the entire contact arc |
| Causes of occurrence | Tension difference on both sides of the belt | The effective pulling force reaches or exceeds the ultimate friction force between the belt and the wheel surface |
| Conclusion | Inevitable | Can avoid |
2.2 Fatigue Failure of the Belt
The stress on the transmission belt varies as it operates, forming an alternating stress. The higher the rotational speed and the shorter the belt, the more frequently the belt wraps around the pulley per unit of time, leading to more frequent changes in stress. Over time, the repeated effect of alternating stress can cause the belt to delaminate and tear, ultimately leading to fatigue failure, which results in transmission failure.
The transmission belt, when installed on the pulley, should have a certain tension to ensure the normal operation of the belt drive. However, after operating for a period of time, the plastic deformation of the belt can lead to slack, gradually reducing the initial tension and diminishing the belt’s load-bearing capacity.
To control the initial tension of the transmission belt and ensure the operational capability of the belt drive, an appropriate tensioning device must be used. Several commonly used tensioning devices are shown in Figure 8-11.
In horizontally arranged or moderately inclined belt drives, a tensioning device as shown in Figure 8-11(a) can be used. The position of the motor, equipped with a pulley, is adjusted using a screw to increase the center distance, thus achieving tensioning. The adjustment method is to mount the motor on a slide rail, and during the initial tensioning of the belt, the motor is pushed to the desired position using the adjustment screw.
In vertical or near-vertical belt drives, a tensioning device as shown in Figure 8-11(b) can be used. By adjusting the position of the swing frame (motor shaft center), the center distance is increased to achieve tensioning. The adjustment method involves adjusting the nut on the screw, causing the machine base to swing around the fixed support shaft to adjust the initial tension. Once the position is adjusted, the nut needs to be locked.
Figure 8-11(c) depicts an automatic tensioning device, where the motor, equipped with a pulley, is mounted on a floating swing frame. Utilizing the weight of the motor and swing frame, the pulley and motor swing around the fixed support shaft, automatically adjusting the center distance to achieve tensioning. This method is commonly used for belt drives with low power transmission and near-vertical arrangement.
Figure 8-11(e) shows a tensioning wheel automatically pressing on the belt due to a weight, thereby achieving tensioning. This method is often used in flat belt drives with a large transmission ratio and small center distance, and it has a significant impact on the lifespan of the belt.
When the center distance of the belt drive cannot be adjusted, a tension pulley can be used to tension the belt, as shown in Figure 8-11(d). The tension pulley is generally installed on the inside of the slack side to allow the belt to undergo unidirectional bending. To prevent the wrap angle of the small pulley from decreasing excessively, the tension pulley should be installed as close as possible to the large pulley.
1. The linear speed of the V-belt should not exceed 25 meters per second, and the flat belt’s linear speed is generally 10-20 meters per second. In special cases, it can be reduced. Belt linear speed can be calculated with the following formula:
V = πDn / 60 x 1000 (meters/second)
Where
2. The number of times the small belt pulley is passed by the flat belt per second, C, should not exceed 3-5 times, and for the V-belt, it should not exceed 20 times.
C = V / L (times / second)
Where L— Belt length (m)
3. The wrap angle of the small V-belt pulley should not be less than 120° (150° for the flat belt), otherwise, the diameter difference between the two belt pulleys should be reduced, the center distance should be increased, or a pressure pulley should be installed.
4. The diameter of the small belt pulley should not be too small to avoid excessive bending of the belt, which shortens its lifespan.
For flat belt drives, the diameter of the small belt pulley should generally be more than 25-30 times the thickness of the cloth tape.
The minimum diameter of the small flat belt pulley, D_min, can be calculated using the formula:
Dmin = C³√N / n1 (mm)
Where
For V-belt drives, the diameter of the small V-belt pulley should not be less than the following values. Otherwise, the wrap angle is not enough, and the belt is prone to slippage and damage.
| V-Belt Model | O | A | B | C | D | E | F |
| Minimum Diameter of Small Pulley (mm) | 70 | 100 | 148 | 200 | 315 | 500 | 800 |
5. The center distance of flat belt pulleys should be more than twice the sum of the two wheel diameters; the center distance of V-belt pulleys should be more than half the sum of the two wheel diameters, but should not exceed twice the sum.
6. Belt length L can be calculated by the following formula:
L=2A + π/2(D1+D2) + (D2-D1)²/4A [mm (open transmission)]
In the formula, A represents the center distance between the two belt pulleys (mm), and D2 and D1 denote the diameters of the large and small belt pulleys (mm), respectively.
7. The initial tension of the belt should be tightened with a force of around 16-18 kg per square centimeter of belt cross-sectional area.
1. For flat belt transmission, the cross-sectional area of the belt can be calculated based on the power used for transmission and the linear speed of the belt.
F=P/K (cm²)
In this formula,
K represents the actual effective stress, kg/cm². For rubber belts, K can be chosen within the range of 10-25 kg/cm². When the linear speed is high, load impact is large, starting load is large, continuous work time is long, and wrap angle is small, a smaller value can be chosen; otherwise, a larger value can be chosen.
Based on the calculated cross-sectional area, the width and thickness of the belt can be determined. With each layer of the belt approximately 1.2 mm thick, the number of layers in a flat belt can be approximated.
2. For V-belt transmission, refer to the following table to determine the type of V-belt based on the transmitted power.
The power range applicable to various types of V-belts.
| Power Transmission (kW) | 0.4-0.75 | 0.75-2.2 | 2.2-3.7 | 3.7-7.5 | 7.5-20 | 20-40 | 40-75 | 75-150 | above 150 |
| Recommended Model | O | O、A | O,A,B | A,B | B,C | C,D | D,E | E,F | F |
The number of V-belts, Z, can be calculated using the following formula:
Z = N / (Z0 * C1 * C2) ^ 0.5
Where:
| Belt wrap angle a° | 180 | 170 | 160 | 150 | 140 | 130 | 120 | 110 | 100 |
| C1 | 1.0 | 0.97 | 0.94 | 0.91 | 0.88 | 0.85 | 0.82 | 0.79 | 0.76 |
C2 – Working Condition Coefficient; 0.6-0.7.
The dimensions of the V-belt pulley groove (see figure) can be found in the table below.
Power (in kW) transmitted by a single V-belt.
| Model | Small Belt Pulley Diameter D1 (mm) | Belt Speed (m/s) | |||
| 5 | 10 | 15 | 20 | ||
| O | 50～63 | 0.31 | 0.59 | 0.88 | 1.07 |
| 80 | 0.38 | 0.74 | 1.04 | 1.29 | |
| ＞90 | 0.42 | 0.82 | 1.14 | 1.40 | |
| A | 80～90 | 0.59 | 1.04 | 1.32 | 1.33 |
| 100 | 0.66 | 1.18 | 1.51 | 1.64 | |
| ＞125 | 0.81 | 1.47 | 1.87 | 2.21 | |
| B | 125 | 1.02 | 1.84 | 2.43 | 2.58 |
| 140 | 1.12 | 2.06 | 2.80 | 3.10 | |
| ＞180 | 1.32 | 2.41 | 3.28 | 3.94 | |
| C | 2OO | 1.98 | 3.60 | 4.80 | 5.52 |
| 250 | 2.41 | 4.45 | 6.14 | 7.00 | |
| ＞280 | 2.67 | 4.95 | 6.77 | 7.72 | |
| D | 315 | 3.98 | 7.00 | 9.20 | 9.95 |
| 400 | 5.07 | 9.10 | 12.30 | 14.40 | |
| ＞450 | 5.45 | 9.95 | 13.30 | 15.40 | |
Dimensional Diagram of V-Belt Pulley Grooves
When calculating the transmission ratio, the diameter of the pulley refers to the position D in the diagram, not the outer edge of the wheel. Additionally, consider that the belt has a 1% slippage.
Dimensions of the v-belt pulley groove:
| Groove Dimensions (mm) | Model | ||||||
| O | A | B | C | D | E | F | |
| a | 10 | 13 | 17 | 22 | 32 | 38 | 50 |
| ι | 10 | 13 | 17 | 22 | 30 | 36 | 48 |
| c | 3 | 4 | 5 | 7 | 9 | 12 | 16 |
| t | 12 | 16 | 21 | 27 | 38 | 44 | 58 |
| s | 9 | 12 | 15 | 18 | 23 | 26 | 32 |
| Corresponding slot angle φ | Minimum diameter of the V-belt pulley (in millimeters) | ||||||
| 34° | 70 | 100 | 148 | 200 | 315 | 500 | 800 |
| 36° | 90 | 125 | 180 | 250 | 400 | 710 | 1000 |
| 38° | ≥112 | ≥160 | ≥225 | ≥315 | ≥500 | ≥800 | ≥1250 |
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO