Bend Allowance Calculator (Online & Free)

Understanding Bend Allowance

Bend allowance is a fundamental concept in sheet metal fabrication, essential for achieving accurate dimensions in bent metal parts. It accounts for the elongation of the material that occurs during the bending process, ensuring that the final dimensions of the part match the design specifications.

Definition of Bend Allowance

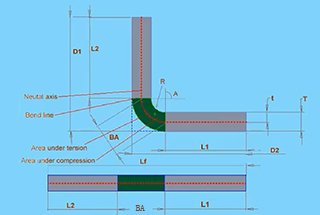
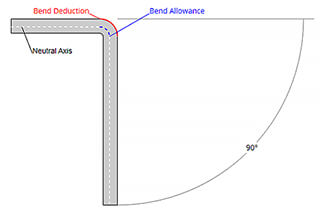
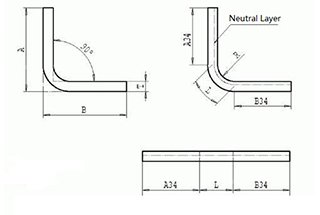
Bend allowance refers to the length of the neutral axis from the beginning to the end of the bend. The neutral axis is an imaginary line within the material that undergoes no compression or elongation during bending. This calculation is crucial for determining the flat pattern layout of a sheet metal part, as it considers the material’s deformation when bent.

Importance in Sheet Metal Design

Accurate calculation of bend allowance is vital for several reasons. First, it ensures that the final dimensions of the bent part match the design specifications. Additionally, it helps in minimizing material waste by accurately predicting the amount of material needed. This reduction in waste leads to cost savings in the manufacturing process by reducing the risk of errors and rework.

Factors Affecting Bend Allowance

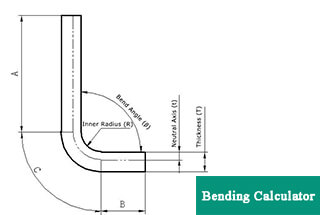
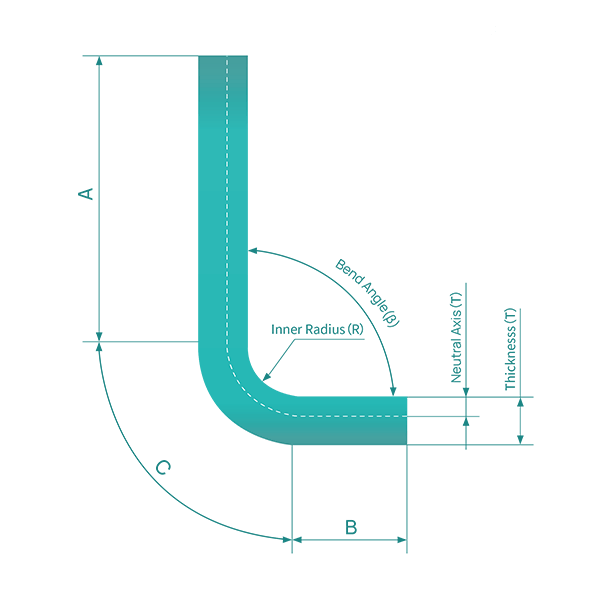
Several factors influence the bend allowance. Material thickness (T) plays a significant role, as thicker materials have different bend characteristics compared to thinner materials. The bend angle (θ), typically measured as the complementary angle, affects how much the material will stretch. The inside radius (r) of the bend on the inside of the material also impacts the calculation. Lastly, the K-factor (K), a material-specific constant representing the ratio between the material thickness and the neutral axis, is crucial.

Bend Allowance Formula

The bend allowance can be calculated using the following formula:

Where:

• ( BA ) is the bend allowance.
• ( θ ) is the bend angle in degrees.
• ( π/180 ) is a conversion factor to convert degrees to radians.
• ( r ) is the inside radius.
• ( K ) is the K-factor.
• ( T ) is the material thickness.

Practical Example

Consider a sheet metal part with the following properties:

• Bend angle (( θ )) = 90°
• Inside radius (( r )) = 5 mm
• Material thickness (( T )) = 2 mm
• K-factor (( K )) = 0.33

Using the bend allowance formula:

This calculation provides the bend allowance needed to develop the flat pattern of the sheet metal part accurately.

I. Bend Allowance Calculator

For new press brake operators who may not be familiar with the intricacies of calculating bend allowance, a bend allowance calculator can be an invaluable tool. This calculator simplifies the process, ensuring accurate results and making daily work more efficient.

Online bend allowance calculators simplify the process by allowing users to input parameters such as material thickness, bend angle, inside radius, and K-factor. These calculators then compute the bend allowance and sometimes the bend deduction, ensuring accurate sheet metal fabrication. By using these tools, manufacturers can save time and reduce the risk of errors in their calculations.

Parameters Required for Calculation

To use the bend allowance calculator effectively, operators need to input the following parameters:

1. Material Thickness: The thickness of the material influences the bend radius and the overall bend allowance.
2. Inside Radius: The radius of the bend on the inside surface of the material.
3. K-Factor: A ratio that helps determine the location of the neutral axis during bending.
4. Bend Angle: The angle at which the material is bent.

Related calculator:

• K Factor Calculator
• Y Factor Calculator
• Bend Deduction Calculator

Further reading:

• How To Calculate Bending Allowance, Bending Deduction And K-Factor?

II. What Is Bend Allowance?

Bend allowance is the additional material length required when bending sheet metal to achieve the desired final dimensions after forming. It compensates for the stretching and compression that occurs in the material during the bending process.The bend allowance varies based on several factors:

1. Material properties: Different materials have different elasticity and plasticity, which affect how much the material stretches or compresses during bending.
2. Sheet thickness: Thicker sheets generally require a larger bend allowance compared to thinner sheets of the same material.
3. Bending method and tooling: The type of bending process (e.g., air bending, bottoming, coining) and the design of the bending die can influence the bend allowance.
4. Inside bend radius: A tighter inside bend radius typically requires a smaller bend allowance than a larger radius.

Bend allowance values are typically determined through a combination of empirical data, mathematical calculations, and practical experience. Experienced sheet metal designers and engineers have developed bend allowance tables and formulas over years of repeated testing and verification.

By using the appropriate bend allowance formula or referring to reliable bend allowance charts, designers can accurately calculate the flat pattern dimensions of a sheet metal part that will yield the desired final bent dimensions. This is crucial for creating accurate flat patterns and ensuring that the bent part fits and functions as intended.

III. Bend Allowance Formula

Bend allowance and bend deduction calculations are essential methods used to determine the length of sheet metal raw materials in their flat form, ensuring the desired size of the bent part is achieved. Understanding these calculations is crucial for precision in sheet metal fabrication.

Bend Allowance Calculation Method:

The bend allowance (BA) is the amount of material that is added to the total length of the flat sheet to account for the material that will be used in the bend. 

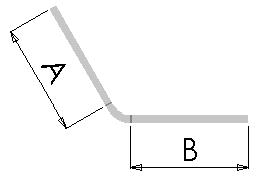
The following equation is used to determine the total flattening length when the bend allowance value is used:

L_t = A + B + BA

Where:

• 𝐿_𝑡 is the total flat length.
• 𝐴 and 𝐵 are the lengths of the two straight sections of the sheet metal before the bend (as shown in the figure).
• 𝐵𝐴 is the bend allowance value.

Bend Deduction Calculation Method:

The bend deduction (BD) is the amount of material that is subtracted from the total length of the flat sheet to account for the material that will be used in the bend. 

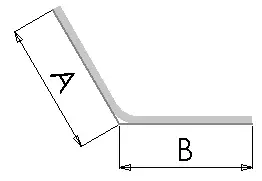
The following equation is used to determine the total flattening length when using the bend deduction value:

L_t = A + B – BD

Where:

• 𝐿_𝑡 is the total flat length.
• 𝐴 and 𝐵 are the lengths of the two straight sections of the sheet metal before the bend (as shown in the figure).
• 𝐵𝐷 is the bend deduction value.

Other Calculation Methods

In addition to the bend allowance and bend deduction methods, other techniques can be used to determine the flat length of sheet metal raw materials. These include:

• Bending Allowance Chart: A pre-calculated chart that provides bend allowance values for various materials and bend angles.
• K-Factor: A ratio that represents the location of the neutral axis relative to the thickness of the material. It is used in more precise bending calculations.
• Bending Calculations: These involve more complex formulas and considerations, such as material properties, bend radius, and thickness, to achieve accurate results.

IV. Bend Allowance Chart

1. Bend allowance chart for SPCC (mild steel)

2. Bend allowance chart for SUS (stainless steel)

3. Bend allowance chart for SPHC (stainless steel)

4. Bend allowance chart for SECC (galvanized steel sheet)

5. Bend allowance chart for aluminum plate

V. Importance of the K-Factor

Definition and Role of the K-Factor

The K-factor is a crucial coefficient in sheet metal fabrication, representing the relative position of the neutral axis within the thickness of the material. The neutral axis is the imaginary plane within the material where no compression or tension occurs during the bending process. The K-factor is calculated as the ratio of the distance from the inner surface to the neutral axis to the total thickness of the material. Understanding the K-factor is essential for accurate bend allowance calculations, ensuring the precision of the final dimensions of bent parts.

Influence on Bend Allowance

The K-factor directly influences the bend allowance, which is the additional length of material needed to accommodate the bend. The bend allowance formula, which typically includes the bend angle, inside radius, material thickness, and K-factor, is:

where ( BA ) is the bend allowance, ( θ ) is the bend angle in radians, ( r ) is the inside radius, ( K ) is the K-factor, and ( T ) is the material thickness. This formula highlights the importance of the K-factor in ensuring that the bend allowance is accurately calculated, which is critical for achieving precise part dimensions and reducing material waste.

Material and Process Dependence

The K-factor is not a constant value and varies depending on several factors, including the properties of the material, the bending method, the bend radius, and the bend angle. Different materials and bending conditions will result in different K-factor values, typically ranging between 0.3 and 0.5. For instance, a material with high ductility may have a different K-factor compared to a more brittle material, influencing the bend allowance and, consequently, the final dimensions of the part.

VI. Practical Application: Step-by-Step Guide

Step 1: Gather Necessary Parameters

To accurately calculate bend allowance and bend deduction, start by collecting the following parameters:

• Material Thickness (T): Measure the thickness of the sheet metal, typically in millimeters (mm) or inches (in).
• Bend Angle (θ): Determine the angle at which the metal sheet will be bent. Common angles include 90°, 120°, etc.
• Inside Radius (IR): Measure the radius of the bend on the inside of the material.
• K-Factor (K): The K-factor represents the ratio of the material’s neutral axis to its thickness and is essential for determining how much material is required for a bend. It usually ranges from 0.3 to 0.5, depending on the material’s properties and thickness.

Step 2: Calculate Bend Allowance (BA)

The bend allowance accounts for the additional length of material required to accommodate the bend. Use the bend allowance formula to determine this value:

Example Calculation:

• Material: Mild Steel
• Thickness (T): 0.125 inches
• Inside Radius (IR): 0.250 inches
• Bend Angle (θ): 90 degrees
• K-Factor (K): 0.42

1. Convert Bend Angle to Radians:

2. Apply the Bend Allowance Formula:

Step 3: Calculate Outside Setback (OSSB)

Next, determine the outside setback, which is important for calculating bend deduction. The formula for OSSB is:

Example Calculation:

• Bend Angle (θ): 90 degrees
• Material Thickness (T): 0.125 inches
• Inside Radius (IR): 0.250 inches

Convert Bend Angle to Radians:

Apply the Outside Setback Formula:

Step 4: Calculate Bend Deduction (BD)

Finally, use the outside setback and bend allowance to determine the bend deduction, which is crucial for achieving accurate dimensions in sheet metal fabrication:

Example Calculation:

• Outside Setback (OSSB): 0.375 inches
• Bend Allowance (BA): 0.475 inches

Apply the Bend Deduction Formula:

Practical Considerations

Understanding the significance of each parameter is vital for successful bending operations. The K-factor, for instance, influences how much material is needed for the bend, while the bend allowance ensures the material will fit correctly after bending. Additionally, it is essential to account for spring back, a phenomenon where the metal returns slightly to its original shape after bending, which may necessitate overbending the material.

By following these steps and carefully considering each parameter, you can accurately calculate the bend allowance and bend deduction necessary for precise sheet metal fabrication.