Have you ever wondered how to precisely calculate the bending allowance for your metal fabrication projects? In this blog post, we’ll explore the fascinating world of bend allowance formulas and calculations. As an experienced mechanical engineer, I’ll guide you through the key concepts and provide practical insights to help you master this crucial aspect of sheet metal design. Get ready to dive in and unlock the secrets of creating accurate and efficient bends in your projects!
Bend allowance is a critical concept in the field of sheet metal fabrication, particularly when working with bending operations. It refers to the additional length of material required to accommodate the bend in the metal sheet. Understanding and accurately calculating bend allowance is essential for ensuring that the final dimensions of the bent part meet the design specifications.
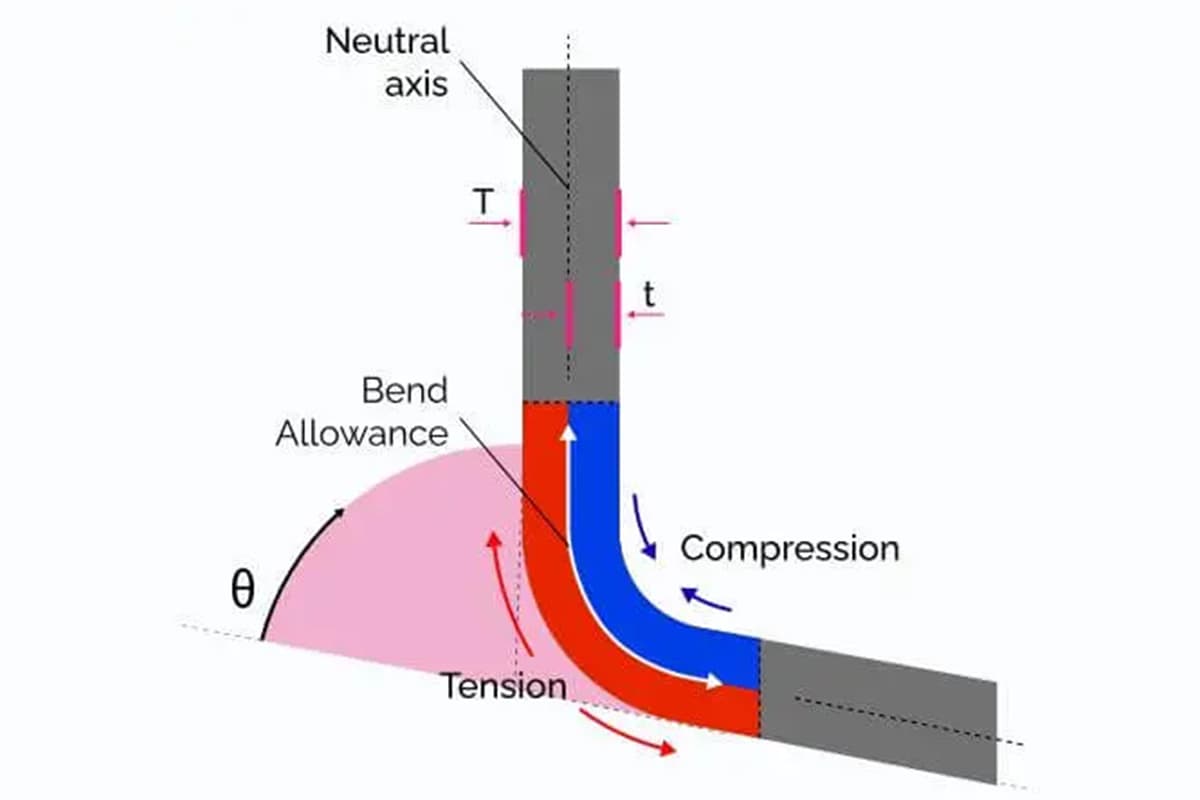
Accurate bend allowance calculations are vital in the fabrication process. When a flat sheet of metal is bent, the material on the outside of the bend stretches, while the material on the inside compresses. Without accounting for this deformation, the final product would not match the intended design, leading to inaccuracies and potential failures. Bend allowance helps fabricators adjust the flat pattern dimensions, ensuring that the bent part meets precise requirements.
Several critical parameters influence bend allowance calculations:
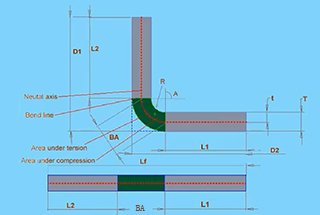
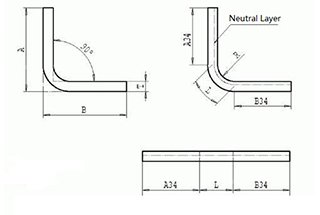
The concept of bending allowance is as follows: when a sheet of metal is bent, it has three dimensions – two outer dimensions (L1 and L2) and one thickness dimension (T).
It is important to note that the sum of L1 and L2 is greater than the unfolded length (L), and the difference between the two is known as the bending allowance (K).
Hence, the unfolded length of a bend can be calculated as L = L1 + L2 – K.
Related reading:
How was the formula for bend allowance created? And how do you calculate bend allowance?
Bend allowance is dependent on the inside formed radius. The lower V die opening determines the inside radius (I.R.) of a formed part. The inside radius for mild steel is 5/32 x lower V die opening (W) when the punch radius is less than 5/32 x W.
If I.R.< Material Thickness (t)
If I.R.> 2 x Material Thickness (t)
Where A= (180 – Bend Included Angle)
If the inside radius is equal to t or 2t, or between t and 2t, the bend allowance is calculated by interpolating the bend allowance values from the two formulas mentioned above.
Besides, to calculate this bending allowance, you can also use the following formula:
This formula considers the diverse geometries and properties of the parts to be formed.
The material thickness (T), bending angle (A), inner bending radius (R), and K-factor of the material to be bent are the most critical factors in this calculation.
As evident from the above formula, calculating the bending allowance is a simple process.
You can determine the bending allowance by substituting the aforementioned values into the formula.
When the bending angle is 90°, the bending allowance formula can be simplified as follows:
Note: The K-factor for most standard materials and thicknesses typically falls between 0 and 0.5.
You can accurately calculate the value of the K-factor using the following K-factor calculator:
The bend allowance (BA) formula is essential for calculating the material length required to form a bend. This general formula is widely applicable across different materials and bending methods:
Where:
The K-factor is crucial as it indicates the position of the neutral axis, which does not change length during bending. Typically, the K-factor ranges between 0.3 and 0.5 and varies based on the type of material, thickness, radius, and bending method.
Different materials have unique properties that necessitate adjustments to the bend allowance calculations. These adjustments ensure accuracy, particularly at 90° bends:
For softer materials like soft brass or copper, the bend allowance is calculated as:
BA = (0.55 × T) + (1.57 × R
This adjustment accounts for the material’s ductility and lower resistance to deformation.
For semi-hard copper or brass, soft steel, and aluminum, the bend allowance is:
BA = (0.64 x T) + (1.57 × R)
These materials have moderate hardness, requiring a slightly higher allowance than softer materials.
For harder materials such as bronze, hard copper, cold-rolled steel, and spring steel, the formula is:
BA = (0.71 x T) + (1.57 × R)
These materials are more resistant to bending, necessitating a higher allowance.
To determine the total flat length of the sheet metal part, the bend allowance is added to the lengths of the flat portions:
Flat Length = Leg Length 1 + BA + Leg Length 2
This approach ensures that the final part dimensions are accurate after bending.
Consider a 90° bend in a sheet of aluminum with a thickness of 2 mm and an inside bend radius of 5 mm. Using the material-specific formula for semi-hard copper, brass, soft steel, and aluminum:
BA = (0.64 × 2) + (1.57 × 5)
BA = 1.28 + 7.85=9.13
If the part has two flat sections of 50 mm each, the total flat length would be:
Flat Length = 50 + 9.13 + 50 = 109.13mm
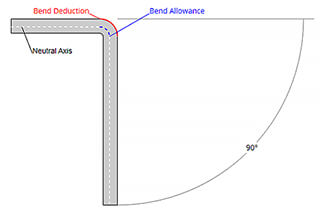
In addition to bend allowance, bend deduction (BD) and outside setback (OSSB) are important for accurate measurements:
Bend Deduction (BD) = OSSB – BA
Where:
These formulations and considerations are essential for accurately calculating bend allowances, ensuring that sheet metal parts are fabricated with the correct dimensions and fit.
Bend allowance is a critical factor in the sheet metal bending process, particularly for materials like aluminum. It accounts for the material stretch that occurs during bending, ensuring accurate final dimensions. Here, we will discuss the specific formula used for aluminum plates and its application.
The bending allowance for an aluminum plate can be calculated using the following formula:
𝐿=𝐿1+𝐿2−1.6𝑇
Where:
The value 1.6𝑇 is derived empirically, meaning it has been established through practical experimentation and production experience. This factor accounts for the material’s behavior during bending, ensuring that the final dimensions are accurate.
It’s crucial to note that this formula is specifically applicable under certain conditions:
To determine the expanded size of the aluminum plate, follow these steps:
This calculation will give you the flat pattern length required before bending, ensuring that the final bent part has the correct dimensions.
The bending allowance calculator provided below simplifies the process of calculating the bending allowance value, which is crucial for accurate sheet metal fabrication. Bend allowance is the length of the neutral axis between the bend lines, which helps in determining the correct blank size for a bent part.
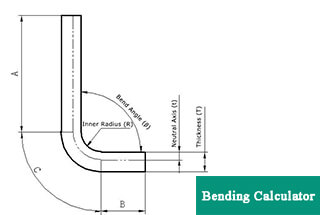
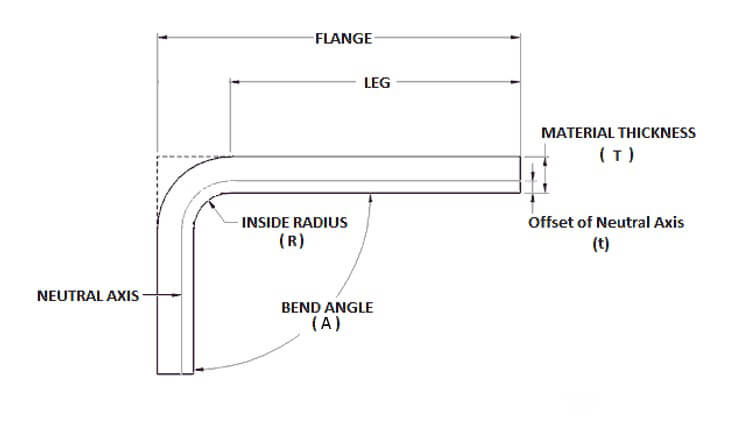
The bend angle, denoted as θ, is a crucial parameter in the bend allowance formula. It represents the angle through which the sheet metal is bent. The bend angle is typically measured in degrees but can be converted to radians using the formula:
The inside radius, represented as r, is the radius of the inner curve of the bend. This radius directly influences the amount of stretching and compressing that occurs within the material during bending. A smaller inside radius results in more significant deformation, which must be accounted for in the bend allowance calculation.
Material thickness, denoted as T, is the thickness of the sheet metal being bent. Thicker materials experience more pronounced stretching and compression, affecting the overall bend allowance. Accurate measurement of material thickness is essential for precise bend allowance calculations.
The K-factor is a dimensionless value that represents the position of the neutral axis relative to the material thickness. The neutral axis is the theoretical line within the material that remains unchanged in length during bending. The K-factor varies based on material properties and bending methods, typically ranging from 0.3 to 0.5 for most materials. The formula for the neutral axis position is:
Neutral Axis Position = K × T
The neutral axis is the imaginary line within the material that remains unchanged in length during bending. Understanding its position is crucial for calculating the correct bend allowance.
Bend allowance, represented as BA, is the length of the neutral axis required to form a bend. It is calculated using the formula:
This formula uses the bend angle, inside radius, material thickness, and K-factor to ensure accurate bend allowance calculations.
The bend allowance chart is an essential resource for professionals working with sheet metal fabrication. It provides a comprehensive listing of key parameters such as material thickness, bending radius, bending angle, bend allowance, and bend deduction values for common materials. This information is crucial for accurately calculating the development length of a sheet metal part after bending.
Further reading:
| TV | Angle | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Shortest size |
| V4 | 90 | 0.9 | 1.4 | 2.8 | ||||||||||
| V4 | 120 | 0.7 | ||||||||||||
| V4 | 150 | 0.2 | ||||||||||||
| V6 | 90 | 1.5 | 1.7 | 2.15 | 4.5 | |||||||||
| V6 | 120 | 0.7 | 0.86 | 1 | ||||||||||
| V6 | 150 | 0.2 | 0.3 | 0.4 | ||||||||||
| V7 | 90 | 1.6 | 1.8 | 2.1 | 2.4 | 5 | ||||||||
| V7 | 120 | 0.8 | 0.9 | 1 | ||||||||||
| V7 | 150 | 0.3 | 0.3 | 0.3 | ||||||||||
| V8 | 90 | 1.6 | 1.9 | 2.2 | 2.5 | 5.5 | ||||||||
| V8 | 30 | 0.3 | 0.34 | 0.4 | 0.5 | |||||||||
| V8 | 45 | 0.6 | 0.7 | 0.8 | 1 | |||||||||
| V8 | 60 | 1 | 1.1 | 1.3 | 1.5 | |||||||||
| V8 | 120 | 0.8 | 0.9 | 1.1 | 1.3 | |||||||||
| V8 | 150 | 0.3 | 0.3 | 0.2 | 0.5 | |||||||||
| V10 | 90 | 2.7 | 3.2 | 7 | ||||||||||
| V10 | 120 | 1.3 | 1.6 | |||||||||||
| V10 | 150 | 0.5 | 0.5 | |||||||||||
| V12 | 90 | 2.8 | 3.65 | 4.5 | 8.5 | |||||||||
| V12 | 30 | 0.5 | 0.6 | 0.7 | ||||||||||
| V12 | 45 | 1 | 1.3 | 1.5 | ||||||||||
| V12 | 60 | 1.7 | 2 | 2.4 | ||||||||||
| V12 | 120 | 1.4 | 1.7 | 2 | ||||||||||
| V12 | 150 | 0.5 | 0.6 | 0.7 | ||||||||||
| V14 | 90 | 4.3 | 10 | |||||||||||
| V14 | 120 | 2.1 | ||||||||||||
| V14 | 150 | 0.7 | ||||||||||||
| V16 | 90 | 4.5 | 5 | 11 | ||||||||||
| V16 | 120 | 2.2 | ||||||||||||
| V16 | 150 | 0.8 | ||||||||||||
| V18 | 90 | 4.6 | 13 | |||||||||||
| V18 | 120 | 2.3 | ||||||||||||
| V18 | 150 | 0.8 | ||||||||||||
| V20 | 90 | 4.8 | 5.1 | 6.6 | 14 | |||||||||
| V20 | 120 | 2.3 | 3.3 | |||||||||||
| V20 | 150 | 0.8 | 1.1 | |||||||||||
| V25 | 90 | 5.7 | 6.4 | 7 | 17.5 | |||||||||
| V25 | 120 | 2.8 | 3.1 | 3.4 | ||||||||||
| V25 | 150 | 1 | 1 | 1.2 | ||||||||||
| V32 | 90 | 7.5 | 8.2 | 22 | ||||||||||
| V32 | 120 | 4 | ||||||||||||
| V32 | 150 | 1.4 | ||||||||||||
| V40 | 90 | 8.7 | 9.4 | 28 | ||||||||||
| V40 | 120 | 4.3 | 4.6 | |||||||||||
| V40 | 150 | 1.5 | 1.6 |
| TV | Angle | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Shortest size |
| V4 | 1.4 | 2.8 | ||||||||||||
| V6 | 1.6 | 4.5 | ||||||||||||
| V7 | 1.6 | 1.8 | 5 | |||||||||||
| V8 | 1.8 | 2.4 | 3.1 | 5.5 | ||||||||||
| V10 | 2.4 | 3.2 | 7 | |||||||||||
| V12 | 2.4 | 3.2 | 8.5 | |||||||||||
| V14 | 3.2 | 10 | ||||||||||||
| V16 | 3.2 | 4 | 4.8 | 11 | ||||||||||
| V18 | 4.8 | 13 | ||||||||||||
| V20 | 4.8 | 14 | ||||||||||||
| V25 | 4.8 | 5.4 | 6 | 17.5 | ||||||||||
| V32 | 6.3 | 6.9 | 22 |
| Angle | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Shortest size |
| 90 | 3.6 | 5.2 | 6.8 | 8.4 | 28 | ||||||||
| 120 | |||||||||||||
| 150 |
| MATERIAL | SPCC | SUS | Al （LY12） | SECC | ||||
|---|---|---|---|---|---|---|---|---|
| T | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK |
| T=0.6 | 1.25 | 1.26 | ||||||
| T=0.8 | 0.18 | 1.42 | 0.15 | 1.45 | 0.09 | 1.51 | ||
| T=1.0 | 0.25 | 1.75 | 0.20 | 1.80 | 0.30 | 1.70 | 0.38 | 1.62 |
| T=1.2 | 0.45 | 1.95 | 0.25 | 2.15 | 0.50 | 1.90 | 0.43 | 1.97 |
| T=1.4 | 0.64 | 2.16 | ||||||
| T=1.5 | 0.64 | 2.36 | 0.50 | 2.50 | 0.70 | 2.30 | ||
| T=1.6 | 0.69 | 2.51 | ||||||
| T=1.8 | 0.65 | 3.00 | ||||||
| T=1.9 | 0.60 | 3.20 | ||||||
| T=2.0 | 0.65 | 3.35 | 0.50 | 3.50 | 0.97 | 3.03 | 0.81 | 3.19 |
| T=2.5 | 0.80 | 4.20 | 0.85 | 4.15 | 1.38 | 3.62 | ||
| T=3.0 | 1.00 | 5.00 | 5.20 | 1.40 | 4.60 | |||
| T=3.2 | 1.29 | 5.11 | ||||||
| T=4.0 | 1.20 | 6.80 | 1.00 | 7.00 | ||||
| T=5.0 | 2.20 | 7.80 | 2.20 | 7.80 | ||||
| T=6.0 | 2.20 | 9.80 | ||||||
Note:
A well-maintained bend allowance chart is a vital tool in the sheet metal fabrication industry. It ensures precision and efficiency in the bending process, ultimately leading to higher quality and more accurate finished products. By understanding and utilizing the values provided in the chart, engineers and fabricators can achieve optimal results in their projects.
In sheet metal fabrication, achieving precision and accuracy is crucial for creating high-quality parts. One of the key factors that play a significant role in this process is the K-Factor. Understanding the K-Factor and its application in bend allowance calculations is essential for fabricators to produce parts that meet exact specifications and perform reliably in various industries.
The K-Factor is a dimensionless value that represents the ratio of the distance from the neutral axis to the material thickness. It is crucial for accurate bend allowance calculations, which determine the amount of material needed to achieve a desired bend. The neutral axis is an imaginary line within the material that does not change in length during bending. By understanding the K-Factor, fabricators can predict how the material will behave when bent, ensuring precise and efficient manufacturing processes.
The K-Factor is calculated using the formula:
Where:
Using the K-Factor in the bend allowance formula helps predict material elongation and compression during bending. The bend allowance formula is:
To illustrate this, let’s walk through a simple example. Suppose we have a sheet metal part with a thickness (T) of 2 mm, bent at a 90-degree angle (θ), with an inside radius (r) of 5 mm, and a K-Factor (K) of 0.4.
1. Convert the bend angle to radians:
2. Apply the values to the bend allowance formula:
This calculation shows that approximately 9.11 mm of material is required along the neutral axis to achieve the desired bend, demonstrating the importance of an accurate K-Factor.
The K-Factor directly impacts the precision of bend allowance calculations. A precise K-Factor ensures that the final dimensions of the bent part match the design specifications, reducing material waste and the need for rework. This precision is vital for industries where exact dimensions are crucial for the assembly and functionality of components.
Different materials have unique mechanical properties, which result in varying K-Factor values. Softer materials like aluminum typically have a lower K-Factor, while harder materials like stainless steel have a higher K-Factor. Understanding these variations allows fabricators to select appropriate K-Factor values for different materials, ensuring accurate calculations and efficient manufacturing processes.
Below are answers to some frequently asked questions:
The bend allowance formula is used to calculate the length of the neutral axis of a bend in sheet metal, which is crucial for determining the correct flat pattern length before the metal is bent. This calculation ensures that the final dimensions of the bent part match the design specifications.
The formula takes into account several key parameters:
The general formula for bend allowance (BA) is:
By using this formula, you can calculate the exact length of material required to form a bend, ensuring that the material neither stretches excessively nor compresses too much. This calculated bend allowance is then added to the leg lengths of the part to develop an accurate flat pattern, which is essential for producing parts with precise dimensions.
The bend allowance formula is also related to bend deduction, which is the length that needs to be subtracted from the total length of the sheet metal to achieve the correct flat pattern. Bend deduction is calculated using the bend allowance and the outside setback, ensuring that the final part dimensions are accurate after bending.
For example, if you are bending a 2mm thick stainless steel sheet to a 90° angle with an inside bend radius of 3mm and a K-factor of 0.44, the bend allowance can be calculated as follows:
This bend allowance is then used to ensure the flat pattern is correctly developed, resulting in a part that meets the design specifications. In summary, the bend allowance formula is essential for accurate sheet metal fabrication, ensuring the final parts are produced to the correct dimensions.
To calculate the bend allowance in sheet metal, you need to determine several key parameters: material thickness (T), bend angle (θ), inside radius (r), and the K-factor (K). The bend allowance (BA) is calculated using the formula:
Here’s a step-by-step process:
Using this formula, for the same parameters:
By following these steps and using the appropriate formula, you can accurately calculate the bend allowance for your sheet metal parts, ensuring precise fabrication.
The K-factor is important in the bend allowance formula for several reasons, each highlighting its significance in precision sheet metal fabrication. Firstly, it represents the ratio of the neutral axis to the material thickness. During bending, the neutral axis shifts from its original location at 50% of the material thickness toward the inside surface of the bend. This shift is critical because it determines the amount of elongation that occurs in the material. The K-factor helps in calculating this new location, which is essential for accurate bend calculations.
Secondly, the K-factor is fundamental in calculating the bend allowance, which is the length of the neutral fiber from the beginning to the end of the arc generated by the bend. This calculation is necessary to determine the flat size of the sheet metal required to achieve the desired bent shape. The bend allowance is directly influenced by the K-factor, as it accounts for the material’s elongation during the bending process.
Additionally, using the K-factor allows for precise calculations of bend deductions, outside setbacks, and the overall flat layout of the part. This precision is vital because it ensures that the final dimensions of the bent part match the design specifications, avoiding errors that could arise from using generic or inaccurate K-factor values.
The K-factor varies based on several parameters, including the material type, thickness, method of forming, tooling, and bend angle. This variability means that the K-factor must be tailored to the specific conditions of the bending process. By considering these factors, the K-factor helps in customizing the bending compensation formula to achieve more accurate results.
Finally, a correct value of the K-factor is essential to avoid errors in the final dimensions of the folded sheet. Incorrect K-factor values can lead to inaccuracies in bend allowances, resulting in parts that do not meet the required specifications. Therefore, accurately determining and using the K-factor is critical for producing high-quality components.
In summary, the K-factor is important because it allows for the precise calculation of bend allowances, accounts for the shift of the neutral axis, and considers the specific material and process parameters, all of which are essential for achieving accurate and reliable results in sheet metal bending.
The bend allowance formula in sheet metal bending commonly includes several key variables:
The bend allowance (BA) can be calculated using the formula:
or
where (0.017453) is (π/180) and (0.0078) is (π /180) x K) – factor.
These variables are essential in accurately determining the bend allowance, which is critical for precise sheet metal fabrication.
Yes, the bend allowance formula can vary significantly based on the material type, as well as other factors such as material thickness, bend angle, and the specific bending process.
The K-factor, a critical component of the bend allowance formula, represents the displacement of the theoretical neutral axis during bending and varies depending on the material. For instance, mild cold-rolled steel typically uses a K-factor around 0.446, whereas other materials like stainless steel and aluminum have different K-factors due to their unique properties and bending behaviors.
The bend allowance formula also incorporates material thickness and bend angle, which can differ across materials. A general form of the bend allowance formula is:
where:
Different materials have distinct properties such as elasticity, tensile strength, and grain direction, which influence their bending behavior. For example, aluminum bends more easily than steel, requiring adjustments in the bend allowance calculation. Additionally, bending a metal along its grain direction can require more force and a different bend allowance compared to bending across the grain.
The material’s tendency to spring back after bending, known as springback, must also be considered. This involves slightly overbending the material to account for elastic recovery, influenced by the material type and its properties.
In summary, the bend allowance formula must be tailored to the specific material being used, considering its unique properties, thickness, and the bending process involved.
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO