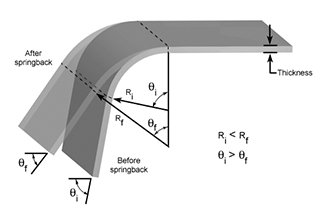
Have you ever wondered why some metal parts spring back after bending? In this article, we’ll explore the fascinating world of bending dies and how to accurately predict springback. You’ll learn practical tips and formulas to achieve precise results in your metalworking projects.
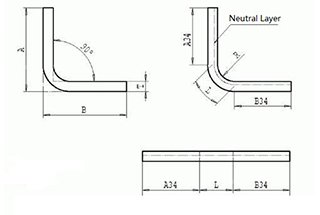
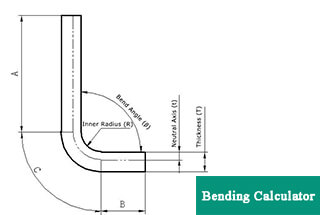
When designing a bending die with an internal arc, precision and material behavior are critical factors often overlooked in conventional approaches. Many designers either neglect springback entirely by using the same radius (R) as the finished product or apply a rudimentary reduction factor to the R value without considering the complexities of material properties and geometries.
For instance, a common practice for a product with an original R value of 1 mm involves reducing the convex mold radius by a factor of 0.8 for harder materials or 0.9 for softer materials. This simplistic approach, while sometimes effective for basic applications, lacks the nuance required for more demanding specifications.
The limitations of this method become particularly apparent when dealing with thin materials and large radii. Consider a product with a thickness of 0.5 mm and an internal radius of 200 mm. In such cases, accurately predicting springback becomes challenging due to the complex interplay between material properties, thickness-to-radius ratio, and bending angle.
To address these limitations and improve precision in die design, a more sophisticated approach is necessary. The following section introduces a universal springback formula that accounts for various material and geometric parameters, allowing for more accurate calculations based on numerical inputs. This method provides a robust foundation for die design across a wide range of applications and materials.
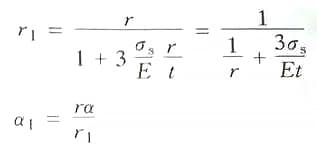
In the formula:
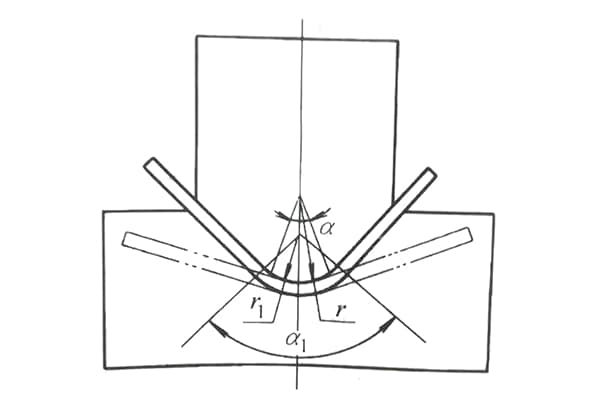
Assuming 3σs/E=A as the simplification coefficient, with values listed in Table 2-27. The calculation formula for the convex die corner radius during the bending of circular section bars is as follows:

The value of A is shown in the table below.
| Material Science | State | A | Material Science | State | A |
| 1035(L4) 8A06(L6) | annealing | 0.0012 | QBe2 | soft | 0.0064 |
| Cold hardness | 0.0041 | hard | 0.0265 | ||
| 2A11(LY11) | soft | 0.0064 | QA15 | hard | 0.0047 |
| hard | 0.0175 | 08, 10, Q215 | 0.0032 | ||
| 2A12(LY12) | soft | 0.007 | 20, Q235 | 0.005 | |
| hard | 0.026 | 30, 35, Q255 | 0.0068 | ||
| T1, T2, T3 | soft | 0.0019 | 50 | 0.015 | |
| hard | 0.0088 | T8 | annealing | 0.0076 | |
| H62 | soft | 0.0033 | cold hardness | ||
| semi-hard | 0.008 | ICr18N9Ti | annealing | 0.0044 | |
| hard | 0.015 | cold hardness | 0.018 | ||
| H68 | soft | 0.0026 | 65Mn | annealing | 0.0076 |
| hard | 0.0148 | cold hardness | 0.015 | ||
| QSn6.5-0.1 | hard | 0.015 | 60Si2MnA | annealing | 0.125 |
If the necessary materials are not available above, you can also refer to the table below to find the modulus of elasticity and yield strength of the material, and then substitute them into the formula above for calculation.
| Material name | Material grade | Material Status | Ultimate Strength | Rate of elongation(%) | Yield strength/MPa | Elastic modulusE/MPa | |
| resisting shear/MPa | tensile/MPa | ||||||
| Carbon structural steel | 30 | Normalized | 440-580 | 550-730 | 14 | 308 | 22000 |
| 55 | 550 | ≥670 | 14 | 390 | – | ||
| 60 | 550 | ≥700 | 13 | 410 | 208000 | ||
| 65 | 600 | ≥730 | 12 | 420 | – | ||
| 70 | 600 | ≥760 | 11 | 430 | 210000 | ||
| Carbon structural steel | T7~T12 T7A-T12A | Annealed | 600 | 750 | 10 | – | – |
| T8A | Cold hardened | 600-950 | 750-1200 | – | – | – | |
| High quality carbon steel | 10Mn2 | Annealed | 320-460 | 400-580 | 22 | 230 | 211000 |
| 65M | 600 | 750 | 18 | 400 | 211000 | ||
| Alloy structural steel | 25CrMnSiA 25CrMnSi | Low-temperature annealed | 400-560 | 500-700 | 18 | 950 | – |
| 30CrMnSiA 30CrMnSi | 440-600 | 550-750 | 16 | 1450850 | – | ||
| High-quality spring steel | 60Si2Mn 60Si2MnA 65Si2WA | Low-temperature annealed | 720 | 900 | 10 | 1200 | 200000 |
| Cold hardened | 640-960 | 800-1200 | 10 | 14001600 | – | ||
| Stainless steel | 1Cr13 | Annealed | 320-380 | 400-170 | 21 | 420 | 210000 |
| 2Cr13 | 320-400 | 400~500 | 20 | 450 | 210000 | ||
| 3Cr13 | 400-480 | 500~600 | 18 | 480 | 210000 | ||
| 4Cr13 | 400-480 | 500-500 | 15 | 500 | 210000 | ||
| 1Cr18Ni9 2Cr18Ni9 | Heat treated | 460~520 | 580-610 | 35 | 200 | 200000 | |
| Cold-hardened | 800-880 | 100-1100 | 38 | 220 | 200000 | ||
| 1Cr18Ni9Ti | Heat treated softened | 430~550 | 54-700 | 40 | 240 | 200000 | |
It is best to establish a commonly used material database and obtain missing physical parameters from suppliers. If the parameters for elastic modulus and yield strength are correct, the bending and rebound of general spring terminals, appearance parts, and profiles are more precise.