Ever thought about how tiny threads can bear immense loads? This article unveils the secrets of metric thread cross-sectional areas and their role in mechanical engineering. Learn how these measurements impact the strength and efficiency of your projects. Dive in to enhance your understanding and boost your engineering prowess!
The cross-sectional area of a bolt is a fundamental parameter in engineering and design, directly influencing the bolt’s mechanical properties and performance. This area is critical for understanding load-bearing capabilities and ensuring the safety and reliability of bolted connections in various applications.
The nominal cross-sectional area is calculated based on the nominal diameter of the bolt, assuming a solid, unthreaded section. This area is often used for initial design calculations.
where ( d ) is the nominal diameter of the bolt.
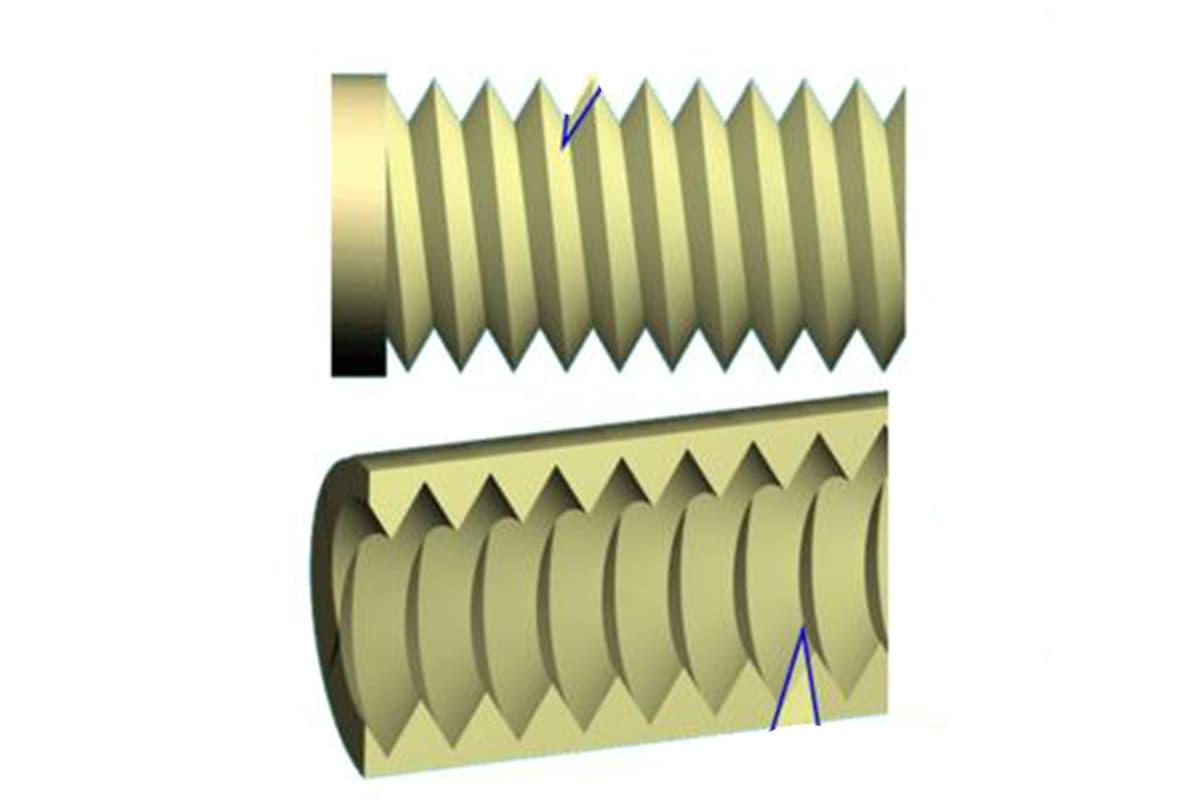
The tensile stress area is the effective cross-sectional area of the threaded portion of the bolt that resists tensile loads. It accounts for the material removed by threading, providing a more accurate measure of the bolt’s strength.
For metric threads:
For inch threads:
where ( d ) is the nominal diameter and ( n ) is the number of threads per unit length.
The root area is based on the minor diameter of the threads, often used in safety-critical applications for a conservative design approach.
For metric threads:
For inch threads:
where ( P ) is the thread pitch.
The cross-sectional area of a bolt is essential in:
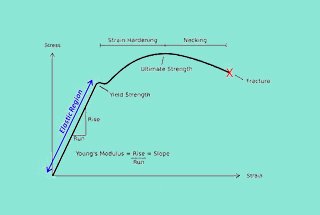
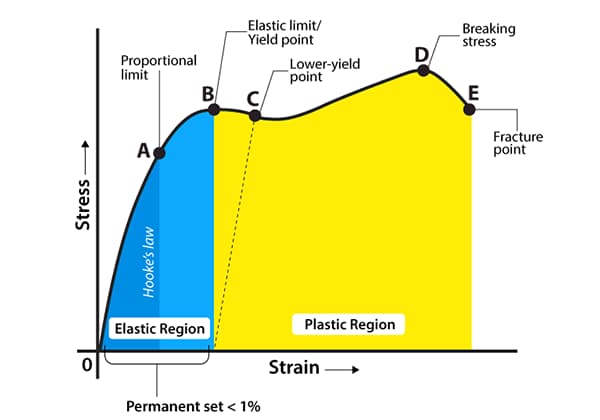
The cross-sectional area of a metric thread is a critical parameter in mechanical engineering, particularly in the design and analysis of fasteners. It determines the load-carrying capacity of the thread. The cross-sectional area, often referred to as the “stress area,” is the effective area that bears the load.
Below is a table listing the thread specification and the corresponding cross-sectional area for standard metric threads. The units for diameter are in millimeters (mm), and the units for cross-sectional area are in square millimeters (mm²).
Standard Source: GB/T16823.1-1997 Stress Cross-Sectional Area and Bearing Area of Threaded Fasteners
| Thread Specification | Pitch (mm) | Cross-Sectional Area (mm2） |
| M1.4 | 0.3 | 0.98 |
| M1.7 | 0.35 | 1.48 |
| M2.0 | 0.4 | 2.07 |
| M2.3 | 0.4 | 2.91 |
| M2.5 | 0.45 | 3.39 |
| M3.0 | 0.5 | 5.03 |
| M3.5 | 0.6 | 6.78 |
| M4.0 | 0.7 | 8.78 |
| M4.5 | 0.75 | 11.32 |
| M5.0 | 0.8 | 14.18 |
| M6.0 | 1 | 20.12 |
| M7.0 | 1 | 28.86 |
| M8.0 | 1.25 | 36.61 |
| M9.0 | 1.25 | 48.12 |
| M10 | 1.5 | 57.99 |
| M11 | 1.5 | 72.27 |
| M12 | 1.75 | 84.27 |
| M14 | 2 | 115.44 |
| M16 | 2 | 156.67 |
| M18 | 2.5 | 192.47 |
| M20 | 2.5 | 244.79 |
| M22 | 2.5 | 303.40 |
| M24 | 3 | 352.50 |
| M27 | 3 | 459.41 |
| M30 | 3.5 | 560.59 |
| M33 | 3.5 | 693.55 |
| M36 | 4 | 816.72 |
| M39 | 4 | 975.75 |
This table provides a quick reference for engineers and designers working with metric threads, facilitating accurate and efficient design and analysis of threaded components.
Understanding the cross-sectional area of a bolt is crucial for determining its strength and performance in various engineering applications. This chapter will explore different types of bolts, the significance of the nominal, tensile stress, and root areas, and provide practical examples of calculations.
Bolts come in various types, each suited for specific applications. Common types include:
The choice of bolt type affects the calculation of the cross-sectional area, especially when considering the tensile stress and root areas.
The cross-sectional area of a bolt is a critical factor in determining its load-bearing capacity. This area influences the bolt’s ability to withstand tensile, shear, and compressive forces. Accurate calculations ensure that the bolt can handle the expected loads without failure.
The nominal cross-sectional area assumes the bolt is a solid cylinder without threading. It provides a baseline measure of the bolt’s diameter. The formula for calculating this area is:
where:
The tensile stress area accounts for the material removed by threading and is crucial for understanding the bolt’s strength under tensile loads. The formulas for calculating the tensile stress area are:
For inch series bolts:
For metric series bolts:
where:
The root area is a conservative measure based on the minor diameter of the threads, often used in safety-critical applications. The formulas are:
For inch series bolts:
For metric series bolts:
For a bolt with a nominal diameter of 0.5 inches:
For a 0.5-inch diameter bolt with 13 threads per inch:
For a 12 mm diameter bolt with a pitch of 1.75 mm:
In engineering applications, selecting the appropriate cross-sectional area depends on the specific requirements and safety margins. While the nominal area is useful for initial estimations, the tensile stress area and root area provide more accurate measures for load-bearing calculations. Ensuring accurate calculations is vital for the bolt’s strength and reliability in various applications, from construction to machinery manufacturing.
In engineering and design, the cross-sectional area of a bolt is crucial for determining the performance and safety of bolted connections. This section explores how this parameter is utilized in real-world scenarios.
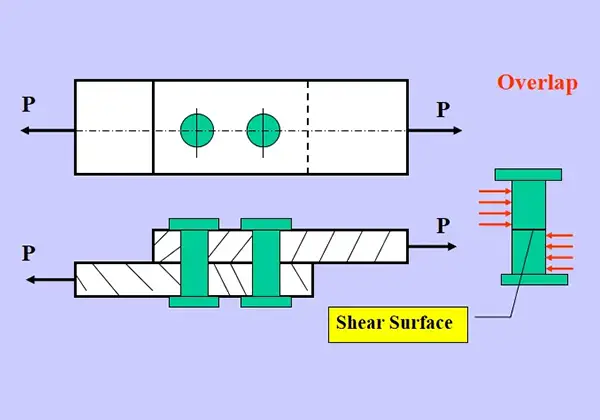
Bolts are often subjected to shear stress, especially in structural connections like lap joints where members overlap. The shear stress ((\tau)) experienced by a bolt is calculated using:
where ( V ) is the shear force acting on the bolt, and ( A_s ) is the cross-sectional area. In double shear configurations, where the load is distributed across two shear planes, the cross-sectional area is considered twice. For example, if a bolt with a cross-sectional area of 50 mm² is subjected to a shear force of 1000 N, the shear stress would be:
Accurate shear stress calculations ensure the bolt can handle the applied loads without failing.
Tensile stress is another critical factor in bolted connections. The tensile stress ((\sigma)) is calculated using:
where ( F ) is the tensile force, and ( A_t ) is the tensile area of the bolt, typically the cross-sectional area of the threaded section. For instance, if a bolt with a tensile area of 78.5 mm² (corresponding to an M10 bolt with a 10 mm nominal diameter) is subjected to a tensile force of 2000 N, the tensile stress would be:
Proper tensile stress calculations help in selecting bolts that can withstand expected tensile loads, preventing failures.
Bearing stress is crucial to prevent local damage to the materials fastened by the bolt. The bearing stress (Σ) is given by:
where ( F ) is the force, ( d_{nom} ) is the nominal diameter of the bolt, and ( t ) is the thickness of the material. For example, if a bolt with a nominal diameter of 12 mm fastens a plate with a thickness of 10 mm under a force of 1500 N, the bearing stress would be:
This calculation ensures the bearing stress remains below the material’s bearing strength.
Choosing the right bolt involves considering the cross-sectional area to handle expected loads. Different types of bolts and materials are used based on specific applications. For example, high-strength steel bolts might be chosen for structural frames, while stainless steel bolts are preferred for corrosion resistance in marine environments. The cross-sectional area helps determine the bolt’s capacity to resist stresses.
In designs with multiple bolts, the total force is distributed among them. The force per bolt is calculated by dividing the connection force by the number of bolts. For instance, if a connection requires a total force of 10,000 N and uses four bolts, each bolt carries 2,500 N. The cross-sectional area of each bolt is then used to determine the stress on each bolt, ensuring even load distribution.
Preload is the initial tension applied to a bolt during installation, influencing joint stiffness and load distribution. The preload ensures the joint members remain clamped and under compression. Joint stiffness depends on the relative stiffness of the bolt and the clamped parts. Properly preloaded bolts enhance the connection’s stability and reliability.
Designing bolted connections involves adhering to industry standards like Eurocode 3 (EN1993) and AISC 360-10. These standards provide criteria for assessing bolt strength, incorporating calculations involving the cross-sectional area. Safety factors and material properties are considered to ensure the connection can handle applied loads effectively and safely.
In summary, the cross-sectional area of a bolt is integral to various engineering and design applications. Accurate determination and application of this parameter ensure the structural integrity and performance of bolted connections under different loading conditions.
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO