Biegegeld-Rechner (online & kostenlos)

Verstehen der Biegezulage

Die Biegezugabe ist ein grundlegendes Konzept in der Blechverarbeitung, das für das Erreichen genauer Abmessungen bei gebogenen Metallteilen unerlässlich ist. Es berücksichtigt die Dehnung des Materials, die während des Biegeprozesses auftritt, und stellt sicher, dass die endgültigen Abmessungen des Teils den Konstruktionsspezifikationen entsprechen.

Definition der Biegezulage

Die Biegezugabe bezieht sich auf die Länge der neutralen Achse vom Anfang bis zum Ende der Biegung. Die neutrale Achse ist eine imaginäre Linie innerhalb des Materials, die während des Biegens keine Stauchung oder Dehnung erfährt. Diese Berechnung ist von entscheidender Bedeutung für die Bestimmung des flachen Musterlayouts eines Blechteils, da sie die Verformung des Materials beim Biegen berücksichtigt.

Bedeutung im Blechdesign

Die genaue Berechnung der Biegezugabe ist aus mehreren Gründen wichtig. Erstens stellt sie sicher, dass die endgültigen Abmessungen des gebogenen Teils mit den Konstruktionsspezifikationen übereinstimmen. Darüber hinaus hilft sie bei der Minimierung des Materialabfalls, indem sie die benötigte Materialmenge genau vorhersagt. Diese Verringerung des Abfalls führt zu Kosteneinsparungen im Fertigungsprozess, da das Risiko von Fehlern und Nacharbeit reduziert wird.

Faktoren, die die Biegezulassung beeinflussen

Mehrere Faktoren beeinflussen die Biegezugabe. Die Materialdicke (T) spielt eine wichtige Rolle, da dickere Materialien im Vergleich zu dünneren Materialien andere Biegeeigenschaften aufweisen. Der Biegewinkel (θ), der in der Regel als Komplementärwinkel gemessen wird, beeinflusst, wie stark sich das Material dehnen wird. Der Innenradius (r) der Biegung auf der Innenseite des Materials wirkt sich ebenfalls auf die Berechnung aus. Schließlich ist der K-Faktor (K), eine materialspezifische Konstante, die das Verhältnis zwischen der Materialdicke und der neutralen Achse darstellt, von entscheidender Bedeutung.

Formel für die Biegezulage

Die Biegezugabe kann nach folgender Formel berechnet werden:

Wo:

• ( BA ) ist die Biegezugabe.
• ( θ ) ist der Biegewinkel in Grad.
• ( π/180 ) ist ein Umrechnungsfaktor zur Umrechnung von Grad in Bogenmaß.
• ( r ) ist der Innenradius.
• ( K ) ist der K-Faktor.
• ( T ) ist die Materialdicke.

Praktisches Beispiel

Betrachten Sie ein Blechteil mit den folgenden Eigenschaften:

• Biegewinkel (( θ )) = 90°
• Innenradius (( r )) = 5 mm
• Materialstärke (( T )) = 2 mm
• K-Faktor (( K )) = 0,33

Verwenden Sie die Formel für die Biegezugabe:

Diese Berechnung liefert die Biegezugabe, die benötigt wird, um das flache Muster des Blechteils genau zu entwickeln.

I. Biegetoleranz-Rechner

Für neue Abkantpresse Wenn Sie mit den Feinheiten der Berechnung von Biegezugaben nicht vertraut sind, kann ein Biegezugabe-Rechner ein unschätzbares Werkzeug sein. Dieser Rechner vereinfacht den Prozess, gewährleistet genaue Ergebnisse und macht die tägliche Arbeit effizienter.

Online-Rechner für Biegezugaben vereinfachen den Prozess, indem sie dem Benutzer die Eingabe von Parametern wie Materialstärke, Biegewinkel, Innenradius und K-Faktor ermöglichen. Diese Rechner berechnen dann die Biegezugabe und manchmal auch den Biegeabzug und gewährleisten so eine genaue Blechfertigung. Durch den Einsatz dieser Werkzeuge können Hersteller Zeit sparen und das Risiko von Fehlern in ihren Berechnungen verringern.

Für die Berechnung erforderliche Parameter

Um den Biegezugabe-Rechner effektiv nutzen zu können, müssen die Bediener die folgenden Parameter eingeben:

1. Material Dicke: Die Dicke des Materials beeinflusst den Biegeradius und die gesamte Biegezugabe.
2. Innerer Radius: Der Radius der Biegung an der Innenfläche des Materials.
3. K-Faktor: Ein Verhältnis, das hilft, die Lage der neutralen Achse während des Biegens zu bestimmen.
4. Biegewinkel: Der Winkel, in dem das Material gebogen wird.

Verwandter Rechner:

• K-Faktor-Rechner
• Y-Faktor-Rechner
• Biegeabzug-Rechner

Lesen Sie weiter:

• Wie berechnet man Biegetoleranz, Biegeabzug und K-Faktor?

II. Was ist Biegezulage?

Die Biegezugabe ist die zusätzliche Materiallänge, die beim Biegen von Blechen benötigt wird, um die gewünschten Endmaße nach dem Umformen zu erreichen. Sie gleicht die Dehnung und Stauchung des Materials während des Biegevorgangs aus, wobei die Biegezugabe von mehreren Faktoren abhängt:

1. Materialeigenschaften: Verschiedene Materialien haben eine unterschiedliche Elastizität und Plastizität, die sich darauf auswirken, wie stark sich das Material beim Biegen dehnt oder staucht.
2. Blechdicke: Dickere Bleche erfordern im Allgemeinen eine größere Biegezugabe als dünnere Bleche desselben Materials.
3. Biegeverfahren und Werkzeugausstattung: Die Art des Biegeverfahrens (z. B. Luftbiegen, Tiefziehen, Prägen) und die Konstruktion des Biegewerkzeugs können die Biegezugabe beeinflussen.
4. Innerer Biegeradius: Ein engerer innerer Biegeradius erfordert in der Regel eine kleinere Biegezugabe als ein größerer Radius.

Die Werte für Biegezugaben werden in der Regel durch eine Kombination aus empirischen Daten, mathematischen Berechnungen und praktischen Erfahrungen ermittelt. Erfahrene Blechkonstrukteure und Ingenieure haben über Jahre hinweg durch wiederholte Tests und Überprüfungen Tabellen und Formeln für Biegezugaben entwickelt.

Mithilfe der entsprechenden Biegezugabeformel oder zuverlässiger Biegezugabentabellen können Konstrukteure die flachen Musterabmessungen eines Blechteils genau berechnen, die die gewünschten endgültigen Biegeabmessungen ergeben. Dies ist entscheidend für die Erstellung präziser flacher Muster und die Gewährleistung, dass das gebogene Teil wie vorgesehen passt und funktioniert.

III. Formel für die Biegezulage

Berechnungen der Biegezugabe und des Biegeabzugs sind wichtige Methoden zur Bestimmung der Länge von Blechrohstoffen in ihrer flachen Form, um sicherzustellen, dass die gewünschte Größe des gebogenen Teils erreicht wird. Das Verständnis dieser Berechnungen ist entscheidend für die Präzision in der Blechfertigung.

Methode zur Berechnung der Biegezulage:

Die Biegezugabe (BA) ist die Materialmenge, die zur Gesamtlänge des flachen Blechs hinzugefügt wird, um das Material zu berücksichtigen, das in der Biegung verwendet wird. 

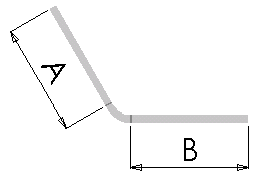
Die folgende Gleichung wird verwendet, um die gesamte Abflachungslänge zu bestimmen, wenn der Wert für die Biegezugabe verwendet wird:

L_t = A + B + BA

Wo:

• 𝐿_𝑡 ist die Gesamtlänge der Wohnung.
• 𝐴 und 𝐵 sind die Längen der beiden geraden Abschnitte des Blechs vor der Biegung (wie in der Abbildung dargestellt).
• 𝐵𝐴 ist der Wert der Biegezugabe.

Methode zur Berechnung des Biegeabzugs:

Der Biegeabzug (BD) ist die Menge an Material, die von der Gesamtlänge des flachen Blechs abgezogen wird, um das Material zu berücksichtigen, das in der Biegung verwendet wird. 

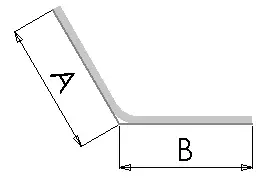
Die folgende Gleichung wird verwendet, um die gesamte Abflachungslänge zu bestimmen, wenn der Wert für den Biegeabzug verwendet wird:

L_t = A + B - BD

Wo:

• 𝐿_𝑡 ist die Gesamtlänge der Wohnung.
• 𝐴 und 𝐵 sind die Längen der beiden geraden Abschnitte des Blechs vor der Biegung (wie in der Abbildung dargestellt).
• 𝐵𝐷 ist der Wert des Biegeabzugs.

Andere Berechnungsmethoden

Zusätzlich zu den Methoden der Biegezugabe und des Biegeabzugs können auch andere Verfahren zur Bestimmung der flachen Länge von Blechrohstoffen verwendet werden. Dazu gehören:

• Biegetoleranztabelle: Eine vorberechnete Tabelle, die Biegezugaben für verschiedene Materialien und Biegewinkel enthält.
• K-Faktor: Ein Verhältnis, das die Lage der neutralen Achse im Verhältnis zur Dicke des Materials angibt. Es wird bei genaueren Biegeberechnungen verwendet.
• Berechnungen zur Biegung: Diese beinhalten komplexere Formeln und Überlegungen, wie z. B. Materialeigenschaften, Biegeradius und Dicke, um genaue Ergebnisse zu erzielen.

IV. Biegetoleranztabelle

1. Tabelle der Biegezugaben für SPCC (Baustahl)

2. Tabelle der Biegezugaben für SUS (rostfreier Stahl)

3. Tabelle der Biegezugaben für SPHC (rostfreier Stahl)

4. Tabelle der Biegezugaben für SECC (verzinktes Stahlblech)

5. Tabelle der Biegezugaben für Aluminiumblech

V. Die Bedeutung des K-Faktors

Definition und Rolle des K-Faktors

Der K-Faktor ist ein wichtiger Koeffizient in der Blechverarbeitung, der die relative Position der neutralen Achse innerhalb der Materialdicke angibt. Die neutrale Achse ist die imaginäre Ebene innerhalb des Materials, in der während des Biegevorgangs keine Druck- oder Zugkräfte auftreten. Der K-Faktor wird berechnet als das Verhältnis zwischen dem Abstand der Innenfläche zur neutralen Achse und der Gesamtdicke des Materials. Die Kenntnis des K-Faktors ist für die genaue Berechnung von Biegezugaben unerlässlich und gewährleistet die Präzision der Endabmessungen von Biegeteilen.

Einfluss auf die Biegezulage

Der K-Faktor wirkt sich direkt auf die Biegezugabe aus, d. h. auf die zusätzliche Länge des Materials, die für die Biegung benötigt wird. Die Formel für die Biegezugabe, die in der Regel den Biegewinkel, den Innenradius, die Materialstärke und den K-Faktor umfasst, lautet:

wobei ( BA ) die Biegezugabe, ( θ ) der Biegewinkel in Radiant, ( r ) der Innenradius, ( K ) der K-Faktor und ( T ) die Materialdicke ist. Diese Formel unterstreicht die Bedeutung des K-Faktors für die genaue Berechnung der Biegezugabe, die für das Erreichen präziser Teileabmessungen und die Reduzierung des Materialabfalls entscheidend ist.

Material- und Prozessabhängigkeit

Der K-Faktor ist kein konstanter Wert und variiert in Abhängigkeit von mehreren Faktoren, darunter die Eigenschaften des Materials, die Biegemethode, der Biegeradius und der Biegewinkel. Unterschiedliche Materialien und Biegebedingungen führen zu unterschiedlichen K-Faktor-Werten, die normalerweise zwischen 0,3 und 0,5 liegen. So kann beispielsweise ein Material mit hoher Duktilität einen anderen K-Faktor aufweisen als ein spröderes Material, was sich auf die Biegezugabe und folglich auf die endgültigen Abmessungen des Teils auswirkt.

VI. Praktische Anwendung: Schritt-für-Schritt-Anleitung

Schritt 1: Erfassen der erforderlichen Parameter

Um die Biegezugabe und den Biegeabzug genau zu berechnen, sollten Sie zunächst die folgenden Parameter erfassen:

• Materialdicke (T): Messen Sie die Dicke des Blechs, normalerweise in Millimetern (mm) oder Zoll (in).
• Biegewinkel (θ): Bestimmen Sie den Winkel, in dem das Blech gebogen werden soll. Übliche Winkel sind 90°, 120° usw.
• Innerer Radius (IR): Messen Sie den Radius der Biegung auf der Innenseite des Materials.
• K-Faktor (K): Der K-Faktor stellt das Verhältnis der neutralen Achse des Materials zu seiner Dicke dar und ist wichtig, um zu bestimmen, wie viel Material für eine Biegung erforderlich ist. Er liegt in der Regel zwischen 0,3 und 0,5, abhängig von den Eigenschaften und der Dicke des Materials.

Schritt 2: Berechnung der Biegezulage (BA)

Die Biegezugabe berücksichtigt die zusätzliche Länge des Materials, die erforderlich ist, um die Biegung unterzubringen. Verwenden Sie die Formel für die Biegezugabe, um diesen Wert zu bestimmen:

Berechnungsbeispiel:

• Material: Baustahl
• Dicke (T): 0,125 Zoll
• Innenradius (IR): 0,250 Zoll
• Biegewinkel (θ): 90 Grad
• K-Faktor (K): 0.42

1. Biegewinkel in Radiant umrechnen:

2. Wenden Sie die Formel für die Biegezulage an:

Schritt 3: Berechnung des Außenabstands (OSSB)

Bestimmen Sie als Nächstes die äußere Absenkung, die für die Berechnung des Knickabzugs wichtig ist. Die Formel für OSSB lautet:

Berechnungsbeispiel:

• Biegewinkel (θ): 90 Grad
• Materialdicke (T): 0,125 Zoll
• Innenradius (IR): 0,250 Zoll

Biegewinkel in Radiant umrechnen:

Wenden Sie die Formel für die äußere Absenkung an:

Schritt 4: Berechnung des Biegeabzugs (BD)

Verwenden Sie schließlich den äußeren Rücksprung und die Biegezugabe, um den Biegeabzug zu bestimmen, der für die Erzielung genauer Abmessungen bei der Blechfertigung entscheidend ist:

Berechnungsbeispiel:

• Äußerer Rücksprung (OSSB): 0,375 Zoll
• Biegezugabe (BA): 0,475 Zoll

Wenden Sie die Formel für den Kurvenabzug an:

Praktische Überlegungen

Das Verständnis der Bedeutung der einzelnen Parameter ist für erfolgreiche Biegevorgänge unerlässlich. Der K-Faktor beeinflusst zum Beispiel, wie viel Material für die Biegung benötigt wird, während die Biegezugabe sicherstellt, dass das Material nach dem Biegen richtig sitzt. Außerdem ist es wichtig, die Rückfederung zu berücksichtigen, ein Phänomen, bei dem das Metall nach dem Biegen leicht in seine ursprüngliche Form zurückkehrt, was eine Überbiegung des Materials erforderlich machen kann.

Wenn Sie diese Schritte befolgen und jeden Parameter sorgfältig berücksichtigen, können Sie die Biegezugabe und den Biegeabzug, die für eine präzise Blechfertigung erforderlich sind, genau berechnen.