Formel für die Biegezulage: Rechner & Diagramme

Was ist die Biegezulage?

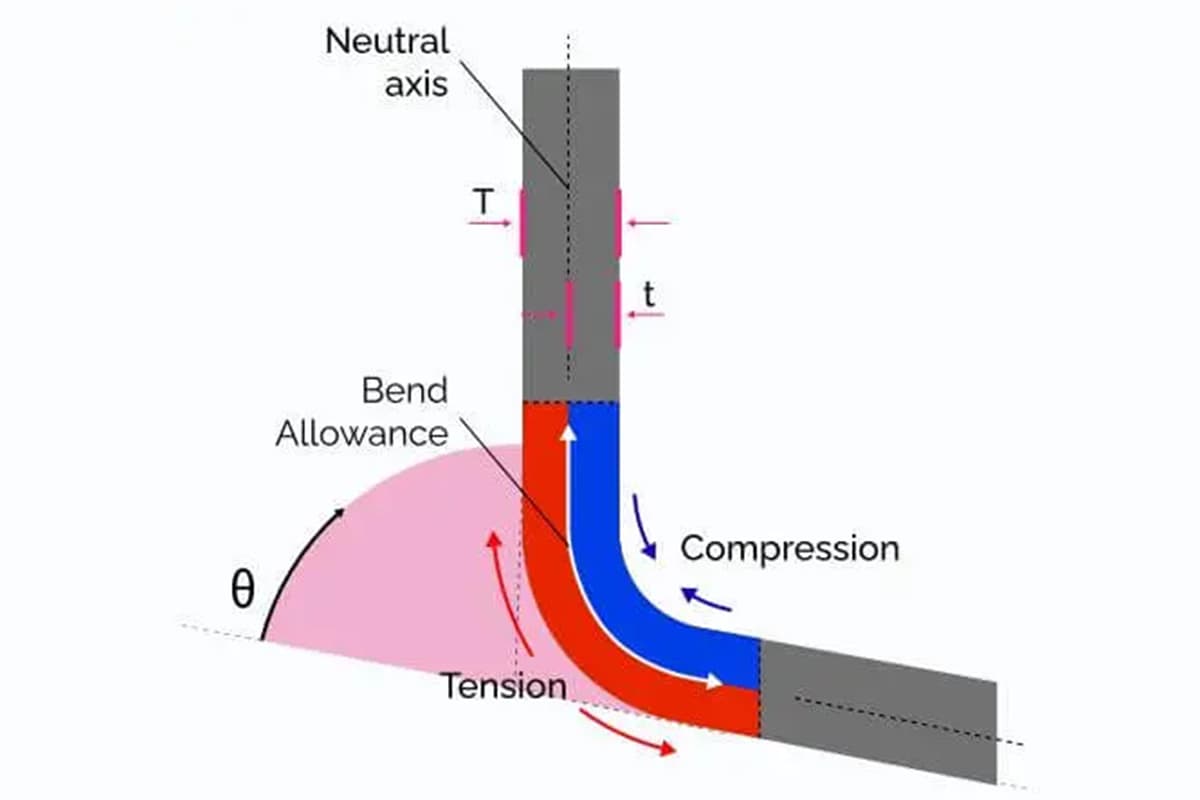
Die Biegezugabe ist ein wichtiger Begriff im Bereich der Blechverarbeitung, insbesondere bei Biegevorgängen. Er bezieht sich auf die zusätzliche Länge des Materials, die erforderlich ist, um die Biegung im Blech unterzubringen. Das Verständnis und die genaue Berechnung der Biegezugabe sind entscheidend, um sicherzustellen, dass die endgültigen Abmessungen des gebogenen Teils den Konstruktionsspezifikationen entsprechen.

Bedeutung in der Blechbearbeitung

Genaue Berechnungen der Biegezugabe sind bei der Herstellung von entscheidender Bedeutung. Wenn ein flaches Metallblech gebogen wird, dehnt sich das Material an der Außenseite der Biegung, während sich das Material an der Innenseite zusammenzieht. Ohne Berücksichtigung dieser Verformung würde das Endprodukt nicht dem geplanten Design entsprechen, was zu Ungenauigkeiten und potenziellen Fehlern führt. Die Biegezugabe hilft den Herstellern, die Abmessungen des flachen Musters anzupassen, um sicherzustellen, dass das gebogene Teil die genauen Anforderungen erfüllt.

Schlüsselparameter, die die Biegezulassung beeinflussen

Mehrere kritische Parameter beeinflussen die Berechnung von Biegezugaben:

• Biegewinkel (θ): Der Winkel, um den das Blech gebogen wird. Bei der Verwendung bestimmter Formeln ist es wichtig, diesen Winkel in Bogenmaß umzurechnen.
• Innenradius (r): Der Radius der Innenkurve der Biegung. Ein kleinerer Radius führt zu einer stärkeren Dehnung und Stauchung, was sich auf die Biegezugabe auswirkt.
• Materialdicke (T): Die Dicke des Blechs. Dickere Materialien weisen beim Biegen eine stärkere Dehnung und Stauchung auf.
• K-Faktor (K): Ein Verhältnis, das die Position der neutralen Achse im Verhältnis zur Materialdicke angibt. Er variiert je nach Materialeigenschaften und Biegeverfahren. Der K-Faktor liegt für die meisten Materialien zwischen 0,3 und 0,5, wobei 0,33 ein üblicher Wert für Baustahl ist.

Das Konzept der Biegezugabe Wenn ein Blech gebogen wird, hat es drei Dimensionen - zwei Außenabmessungen (L1 und L2) und eine Dickenabmessung (T).

Es ist wichtig zu beachten, dass die Summe von L1 und L2 größer ist als die ungefaltete Länge (L), und die Differenz zwischen den beiden wird als Biegezugabe (K) bezeichnet.

Die entfaltete Länge einer Biegung lässt sich also berechnen als L = L1 + L2 - K.

Weiterführende Lektüre:

• Berechnung von Biegetoleranz, Biegeabzug und K-Faktor？

Formel für die Biegezulage

Formel für die Biegezugabe für Stahl

Wie wurde die Formel für Biegezugabe erstellt? Und wie berechnen Sie Biegezugabe?

Die Biegezugabe ist abhängig vom Innenradius der Form. Die untere V-Matrizenöffnung bestimmt den Innenradius (I.R.) eines Formteils. Der Innenradius für Baustahl beträgt 5/32 x untere V-Matrizenöffnung (W), wenn der Stempelradius kleiner als 5/32 x W ist.

Wenn I.R.< Materialdicke (t)

Wenn I.R.> 2 x Materialdicke (t)

Dabei ist A= (180 - eingeschlossener Biegewinkel)

Wenn der Innenradius gleich t oder 2t oder zwischen t und 2t liegt, wird die Biegezugabe durch Interpolation der Biegezugabewerte aus den beiden oben genannten Formeln berechnet.

Außerdem können Sie zur Berechnung dieser Biegezugabe auch die folgende Formel verwenden:

• BA - Biegezulage
• A - biegen Winkel in Grad
• R - innerer Biegeradius in m
• K - konstant
• T - Dicke des Materials in m

Diese Formel berücksichtigt die unterschiedlichen Geometrien und Eigenschaften der zu formenden Teile.

Die Materialstärke (T), der Biegewinkel (A), die innere Biegeradius (R) und der K-Faktor des zu biegenden Materials sind die wichtigsten Faktoren bei dieser Berechnung.

Wie aus der obigen Formel ersichtlich, ist die Berechnung der Biegezugabe ein einfacher Prozess.

Sie können die Biegezugabe ermitteln, indem Sie die oben genannten Werte in die Formel einsetzen.

Wenn der Biegewinkel 90° beträgt, kann die Formel für die Biegezugabe wie folgt vereinfacht werden:

Hinweis: Der K-Faktor für die meisten Standardmaterialien und -dicken liegt normalerweise zwischen 0 und 0,5.

Sie können den Wert des K-Faktors wie folgt genau berechnen K-Faktor-Rechner:

Alternative Knickzulassungsformulierungen

Allgemeine Formel für die Beugezulage

Die Formel für die Biegezugabe (BA) ist wichtig für die Berechnung der für eine Biegung erforderlichen Materiallänge. Diese allgemeine Formel ist auf verschiedene Materialien und Biegeverfahren anwendbar:

Wo:

• ( BA ) ist die Biegezugabe.
• ( Angle ) ist der Biegewinkel in Grad.
• ( Radius ) ist der innere Biegeradius.
• ( K ) ist der K-Faktor, der die Lage der neutralen Achse in Bezug auf die Materialdicke angibt.
• ( Dicke ) ist die Materialdicke.

Der K-Faktor ist von entscheidender Bedeutung, da er die Position der neutralen Achse angibt, deren Länge sich während des Biegens nicht ändert. In der Regel liegt der K-Faktor zwischen 0,3 und 0,5 und variiert je nach Art des Materials, der Dicke, des Radius und der Biegemethode.

Materialspezifische Formulierungen

Verschiedene Materialien haben einzigartige Eigenschaften, die Anpassungen bei der Berechnung der Biegezugabe erforderlich machen. Diese Anpassungen gewährleisten die Genauigkeit, insbesondere bei 90°-Biegungen:

Weichmessing oder Weichkupfer

Bei weicheren Materialien wie weichem Messing oder Kupfer wird die Biegezugabe wie folgt berechnet:

BA = (0,55 × T) + (1,57 × R

Diese Anpassung trägt der Duktilität und dem geringeren Verformungswiderstand des Materials Rechnung.

Halbhartes Kupfer oder Messing, weicher Stahl und Aluminium

Für halbhartes Kupfer oder Messing, weichen Stahl und Aluminium beträgt die Biegezugabe:

BA = (0,64 x T) + (1,57 × R)

Diese Materialien weisen eine mittlere Härte auf und erfordern eine etwas höhere Zulage als weichere Materialien.

Bronze, Hartkupfer, kaltgewalzter Stahl und Federstahl

Für härtere Materialien wie Bronze, Hartkupfer, kaltgewalzten Stahl und Federstahl lautet die Formel:

BA = (0,71 x T) + (1,57 × R)

Diese Materialien sind widerstandsfähiger gegen Biegung, was eine höhere Zulage erforderlich macht.

Berechnung der flachen Länge

Um die gesamte flache Länge des Blechteils zu ermitteln, wird die Biegezugabe zu den Längen der flachen Teile addiert:

Flache Länge = Beinlänge 1 + BA + Beinlänge 2

Auf diese Weise wird sichergestellt, dass die endgültigen Abmessungen des Teils nach dem Biegen genau sind.

Praktisches Beispiel

Betrachten wir eine 90°-Biegung in einem Aluminiumblech mit einer Dicke von 2 mm und einem inneren Biegeradius von 5 mm. Verwenden Sie die materialspezifische Formel für halbhartes Kupfer, Messing, weichen Stahl und Aluminium:

BA = (0,64 × 2) + (1,57 × 5)

BA = 1,28 + 7,85=9,13

Wenn das Teil zwei flache Abschnitte von je 50 mm hat, beträgt die gesamte flache Länge:

Flache Länge = 50 + 9,13 + 50 = 109,13 mm

Kurvenabzug und äußerer Rücksprung

Neben der Biegezugabe sind auch der Biegeabzug (BD) und der Außenabzug (OSSB) für genaue Messungen wichtig:

Biegeabzug (BD) = OSSB - BA

Wo:

• ( OSSB ) ist die äußere Absenkung, berechnet als ( R + T ).
• ( BA ) ist die Biegezugabe.

Diese Formulierungen und Überlegungen sind für die genaue Berechnung von Biegezugaben unerlässlich, um sicherzustellen, dass die Blechteile mit den richtigen Abmessungen und der richtigen Passform hergestellt werden.

Formel für die Biegezugabe für Aluminium

Die Biegezugabe ist ein entscheidender Faktor beim Biegen von Blechen, insbesondere bei Materialien wie Aluminium. Sie berücksichtigt die Materialdehnung, die während des Biegens auftritt, und sorgt für genaue Endmaße. Im Folgenden werden wir die spezifische Formel für Aluminiumbleche und ihre Anwendung erörtern.

Erläuterung der Formel

Die Biegezugabe für eine Aluminiumplatte kann mit der folgenden Formel berechnet werden:

𝐿=𝐿1+𝐿2-1.6𝑇

Wo:

• 𝐿 ist die Gesamtlänge des flachen Musters (erweiterte Größe).
• 𝐿1 und 𝐿2 sind die beiden Biegelängen.
• 𝑇 ist die Dicke der Aluminiumplatte.
• 1,6𝑇 ist der empirische Wert für die Biegezugabe.

Empirischer Wert

Der Wert 1,6𝑇 ist empirisch abgeleitet, d. h. er wurde durch praktische Experimente und Produktionserfahrungen ermittelt. Dieser Faktor berücksichtigt das Verhalten des Materials beim Biegen und stellt sicher, dass die endgültigen Abmessungen genau sind.

Anwendungsbedingungen

Es ist wichtig zu wissen, dass diese Formel nur unter bestimmten Bedingungen anwendbar ist:

• Die Biegeöffnung (der Abstand zwischen den Biegelinien) sollte das 6-fache der Dicke des Aluminiumblechs betragen. Dadurch wird sichergestellt, dass das Verhalten des Materials mit dem in der Formel verwendeten empirischen Wert übereinstimmt.

Praktische Anwendung

Führen Sie die folgenden Schritte aus, um die erweiterte Größe der Aluminiumplatte zu bestimmen:

1. Messen Sie die beiden Biegelängen 𝐿1 und 𝐿2.
2. Messen Sie die Dicke 𝑇 der Aluminiumplatte.
3. Wenden Sie die Formel 𝐿=𝐿1+𝐿2-1,6𝑇 an.

Aus dieser Berechnung ergibt sich die vor dem Biegen benötigte Länge des flachen Musters, wodurch sichergestellt wird, dass das endgültige Biegeteil die richtigen Abmessungen hat.

Rechner für die Biegezulage

Der unten stehende Biegezugabe-Rechner vereinfacht die Berechnung des Biegezugabewertes, der für eine genaue Blechfertigung entscheidend ist. Die Biegezugabe ist die Länge der neutralen Achse zwischen den Biegelinien, die bei der Bestimmung der richtigen Zuschnittgröße für ein gebogenes Teil hilft.

Verstehen der Variablen

Biegewinkel (θ)

Der Biegewinkel, bezeichnet als θ, ist ein entscheidender Parameter in der Formel für die Biegezugabe. Er stellt den Winkel dar, um den das Blech gebogen wird. Der Biegewinkel wird in der Regel in Grad gemessen, kann aber mithilfe der Formel in Bogenmaß umgerechnet werden:

Innenradius (r)

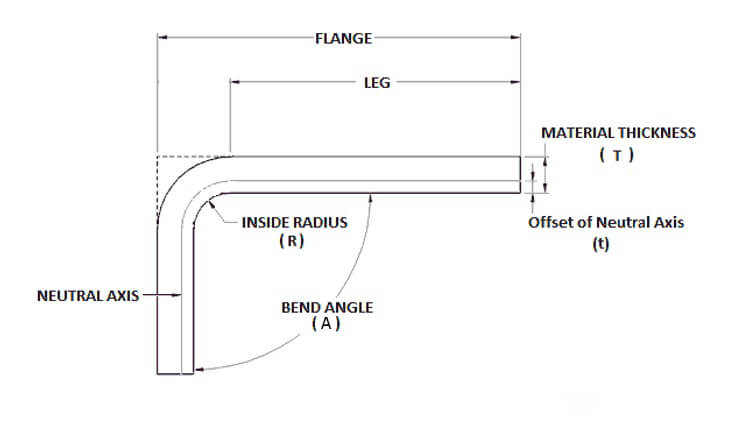
Der Innenradius, dargestellt als r, ist der Radius der Innenkurve der Biegung. Dieser Radius hat direkten Einfluss auf das Ausmaß der Dehnung und Stauchung, die während des Biegens im Material auftreten. Ein kleinerer Innenradius führt zu einer stärkeren Verformung, die bei der Berechnung der Biegezugabe berücksichtigt werden muss.

Materialdicke (T)

Die Materialstärke, bezeichnet mit T, ist die Dicke des zu biegenden Blechs. Dickere Materialien werden stärker gedehnt und gestaucht, was sich auf die Gesamtbiegezugabe auswirkt. Eine genaue Messung der Materialdicke ist für eine präzise Berechnung der Biegezugabe unerlässlich.

K-Faktor (K)

Der K-Faktor ist ein dimensionsloser Wert, der die Lage der neutralen Achse in Bezug auf die Materialdicke angibt. Die neutrale Achse ist die theoretische Linie innerhalb des Materials, die während des Biegens in ihrer Länge unverändert bleibt. Der K-Faktor variiert je nach Materialeigenschaften und Biegemethode und liegt für die meisten Materialien zwischen 0,3 und 0,5. Die Formel für die Position der neutralen Achse lautet:

Neutrale Achsenposition = K × T

Neutrale Achse

Die neutrale Achse ist die imaginäre Linie im Material, die beim Biegen in ihrer Länge unverändert bleibt. Die Kenntnis ihrer Position ist entscheidend für die Berechnung der korrekten Biegezugabe.

Biegezulage (BA)

Die Biegezugabe, dargestellt als BA, ist die Länge der neutralen Achse, die erforderlich ist, um eine Biegung zu bilden. Sie wird nach der folgenden Formel berechnet:

Diese Formel verwendet den Biegewinkel, den Innenradius, die Materialstärke und den K-Faktor, um eine genaue Berechnung der Biegezugabe zu gewährleisten.

Biegetoleranztabelle

Die Tabelle der Biegezugaben ist ein wichtiges Hilfsmittel für Fachleute, die mit der Herstellung von Blechen arbeiten. Sie bietet eine umfassende Auflistung der wichtigsten Parameter wie Materialstärke, Biegeradius, Biegewinkel, Biegezugabe und Biegeabzugswerte für gängige Materialien. Diese Informationen sind entscheidend für die genaue Berechnung der Entwicklungslänge eines Blechteils nach dem Biegen.

Lesen Sie weiter:

• Biegeabzug-Rechner

(1) Biegetabelle für kaltgewalztes Stahlblech SPCC (galvanisch verzinktes Blech SECC)

(2) Biegezugabe-Tabelle für Aluminiumblech

(3) Biegezugabe-Tabelle für Kupferblech

• Laden Sie die PDF-Datei mit der Tabelle der Biegezugaben herunter

(4) Amada Biegetoleranztabelle

Anmerkung:

• Der V12-Koeffizient für 2 mm C-Profil beträgt 3,65 und der für andere 2 mm-Bleche 3,5). Die Falzbiegezugabe für 2mm-Blech beträgt 1,4;
• Die Biegezugabe für 6 mm Kupferblech beträgt 10,3;
• Die Biegezugabe für 8 mm Kupferblech beträgt 12,5;
• Die Biegezugabe für 10 mm Kupferblech beträgt 15;
• Die Biegezugabe für 12 mm Kupferblech beträgt 17;
• Die Biegezugabe für rostfreien Stahl 3.0 mit V25-Matrize beträgt 6;
• Die Biegezugabe für rostfreien Stahl 3.0 mit V20-Matrize beträgt 5,5;
• (Die Kupferschienen mit einer Länge von mehr als 6 mm verwenden alle die Biegezugabe von V40 Untergesenk)

Eine gut geführte Biegeaufmaßtabelle ist ein wichtiges Werkzeug in der Blechverarbeitung. Sie gewährleistet Präzision und Effizienz im Biegeprozess, was letztlich zu einer höheren Qualität und genaueren Endprodukten führt. Durch das Verständnis und die Nutzung der in der Tabelle angegebenen Werte können Ingenieure und Verarbeiter optimale Ergebnisse bei ihren Projekten erzielen.

Die Bedeutung des K-Faktors

Einführung

Bei der Blechbearbeitung sind Präzision und Genauigkeit entscheidend für die Herstellung hochwertiger Teile. Einer der Schlüsselfaktoren, die bei diesem Prozess eine wichtige Rolle spielen, ist der K-Faktor. Das Verständnis des K-Faktors und seiner Anwendung bei der Berechnung von Biegezugaben ist für Verarbeiter unerlässlich, um Teile herzustellen, die exakte Spezifikationen erfüllen und in verschiedenen Branchen zuverlässig funktionieren.

Definition des K-Faktors

Der K-Faktor ist ein dimensionsloser Wert, der das Verhältnis zwischen dem Abstand von der neutralen Achse und der Materialdicke darstellt. Er ist ausschlaggebend für genaue Berechnungen der Biegezugabe, die die Materialmenge bestimmt, die zum Erreichen einer gewünschten Biegung benötigt wird. Die neutrale Achse ist eine imaginäre Linie innerhalb des Materials, deren Länge sich während des Biegens nicht ändert. Durch die Kenntnis des K-Faktors können Verarbeiter vorhersagen, wie sich das Material beim Biegen verhält, und so präzise und effiziente Fertigungsprozesse gewährleisten.

Berechnung und Rolle bei der Biegezulage

Der K-Faktor wird nach der folgenden Formel berechnet:

Wo:

• ( t ) ist der Abstand von der Innenfläche zur neutralen Achse.
• ( T ) ist die Materialdicke.

Die Verwendung des K-Faktors in der Formel für die Biegezugabe hilft bei der Vorhersage der Materialdehnung und -kompression beim Biegen. Die Formel für die Biegezugabe lautet:

Um dies zu veranschaulichen, gehen wir ein einfaches Beispiel durch. Angenommen, wir haben ein Blechteil mit einer Dicke (T) von 2 mm, das in einem 90-Grad-Winkel (θ) gebogen ist, mit einem Innenradius (r) von 5 mm und einem K-Faktor (K) von 0,4.

1. Konvertieren Sie den Biegewinkel in Radiant:

2. Setzen Sie die Werte in die Formel für die Biegezugabe ein:

Diese Berechnung zeigt, dass etwa 9,11 mm Material entlang der neutralen Achse erforderlich sind, um die gewünschte Biegung zu erreichen, was die Bedeutung eines genauen K-Faktors zeigt.

Einfluss auf die Konstruktion von Blechen

Präzision und Genauigkeit

Der K-Faktor wirkt sich direkt auf die Genauigkeit der Berechnung von Biegezugaben aus. Ein präziser K-Faktor stellt sicher, dass die endgültigen Abmessungen des gebogenen Teils mit den Konstruktionsspezifikationen übereinstimmen, wodurch der Materialabfall und die Notwendigkeit zur Nacharbeit verringert werden. Diese Präzision ist für Branchen, in denen exakte Abmessungen für die Montage und Funktionalität von Bauteilen entscheidend sind, von entscheidender Bedeutung.

Materialeigenschaften

Verschiedene Materialien haben einzigartige mechanische Eigenschaften, die zu unterschiedlichen K-Faktor-Werten führen. Weichere Materialien wie Aluminium haben in der Regel einen niedrigeren K-Faktor, während härtere Materialien wie Edelstahl einen höheren K-Faktor haben. Das Wissen um diese Unterschiede ermöglicht es den Verarbeitern, geeignete K-Faktor-Werte für verschiedene Materialien auszuwählen, um genaue Berechnungen und effiziente Fertigungsprozesse zu gewährleisten.

Häufig gestellte Fragen

Nachstehend finden Sie Antworten auf einige häufig gestellte Fragen:

Wofür wird die Formel für die Knickzulage verwendet?

Die Formel für die Biegezugabe wird verwendet, um die Länge der neutralen Achse einer Biegung in Blech zu berechnen, was für die Bestimmung der korrekten Länge des flachen Musters vor dem Biegen des Metalls entscheidend ist. Durch diese Berechnung wird sichergestellt, dass die endgültigen Abmessungen des gebogenen Teils den Konstruktionsspezifikationen entsprechen.

Bei der Formel werden mehrere Schlüsselparameter berücksichtigt:

• Biegewinkel (A): Der Winkel der Biegung, gemessen in Grad oder Radiant.
• Innenradius (R): Der Radius der Biegung an der Innenseite der Kurve.
• K-Faktor (K): Ein Faktor, der das Verhalten des Materials beim Biegen berücksichtigt, insbesondere seine Tendenz, sich an der Außenfläche zu dehnen und an der Innenfläche zu stauchen.
• Materialdicke (T): Die Dicke des Blechs.

Die allgemeine Formel für die Biegezugabe (BA) lautet:

Mit dieser Formel können Sie die genaue Länge des Materials berechnen, die für eine Biegung erforderlich ist, wobei sichergestellt wird, dass das Material weder übermäßig gedehnt noch zu stark zusammengedrückt wird. Diese berechnete Biegezugabe wird dann zu den Schenkellängen des Teils addiert, um ein genaues flaches Muster zu entwickeln, das für die Herstellung von Teilen mit präzisen Abmessungen unerlässlich ist.

Die Formel für die Biegezugabe steht auch im Zusammenhang mit dem Biegeabzug, d. h. der Länge, die von der Gesamtlänge des Blechs abgezogen werden muss, um das richtige flache Muster zu erhalten. Der Biegeabzug wird anhand der Biegezugabe und des Außenabschlags berechnet, um sicherzustellen, dass die endgültigen Abmessungen des Teils nach dem Biegen genau sind.

Wenn Sie zum Beispiel ein 2 mm dickes Edelstahlblech zu einem 90°-Winkel mit einem inneren Biegeradius von 3 mm und einem K-Faktor von 0,44 biegen, kann die Biegezugabe wie folgt berechnet werden:

Diese Biegezugabe wird dann verwendet, um sicherzustellen, dass das flache Muster korrekt entwickelt wird, was zu einem Teil führt, das den Konstruktionsspezifikationen entspricht. Zusammenfassend lässt sich sagen, dass die Formel für die Biegezugabe für eine genaue Blechfertigung unerlässlich ist, um sicherzustellen, dass die endgültigen Teile mit den richtigen Abmessungen hergestellt werden.

Wie berechnet man die Biegezugabe bei Blechen?

Zur Berechnung der Biegezugabe in Blechen müssen Sie mehrere Schlüsselparameter bestimmen: Materialstärke (T), Biegewinkel (θ), Innenradius (r) und den K-Faktor (K). Die Biegezugabe (BA) wird mit der folgenden Formel berechnet:

Hier eine Schritt-für-Schritt-Anleitung:

1. Parameter sammeln: Ermitteln Sie die Materialstärke (T), den Biegewinkel (θ), den Innenradius (r) und den K-Faktor (K). Der Biegewinkel sollte der Komplementärwinkel sein, d. h. der Winkel außerhalb der Biegung.
2. Biegewinkel umrechnen: Wenn der Biegewinkel in Grad angegeben ist, können Sie ihn direkt in die Formel einsetzen. Wenn er im Bogenmaß angegeben ist, muss er entsprechend umgerechnet werden.
3. Anwendung der Formel: Verwenden Sie die Formel, um die Biegezugabe zu berechnen. Wenn der Biegewinkel beispielsweise 120 Grad beträgt, der Innenradius 0,062 Zoll, die Materialstärke 0,062 Zoll und der K-Faktor 0,446:

4. Alternative Berechnung: Eine andere gängige Formel ist:

Mit dieser Formel, für die gleichen Parameter:

5. Biegezulage anwenden: Addieren Sie die berechnete Biegezugabe zu den Schenkellängen des Teils, um die richtige Größe des flachen Musters zu bestimmen.

Wenn Sie diese Schritte befolgen und die entsprechende Formel verwenden, können Sie die Biegezugabe für Ihre Blechteile genau berechnen und eine präzise Fertigung gewährleisten.

Warum ist der K-Faktor in der Formel für das Biegegeld wichtig?

Der K-Faktor ist in der Formel für die Biegezugabe aus mehreren Gründen wichtig, von denen jeder seine Bedeutung für die Präzisionsblechfertigung unterstreicht. Erstens stellt er das Verhältnis zwischen der neutralen Achse und der Materialdicke dar. Während des Biegens verschiebt sich die neutrale Achse von ihrer ursprünglichen Position bei 50% der Materialdicke in Richtung der Innenfläche der Biegung. Diese Verschiebung ist von entscheidender Bedeutung, da sie das Ausmaß der im Material auftretenden Dehnung bestimmt. Der K-Faktor hilft bei der Berechnung dieser neuen Position, die für genaue Biegeberechnungen unerlässlich ist.

Zweitens ist der K-Faktor grundlegend für die Berechnung der Biegezugabe, d. h. der Länge der neutralen Faser vom Anfang bis zum Ende des durch die Biegung erzeugten Bogens. Diese Berechnung ist notwendig, um die flache Größe des Blechs zu bestimmen, die erforderlich ist, um die gewünschte Biegeform zu erreichen. Die Biegezugabe wird direkt durch den K-Faktor beeinflusst, da er die Dehnung des Materials während des Biegevorgangs berücksichtigt.

Darüber hinaus ermöglicht die Verwendung des K-Faktors präzise Berechnungen von Biegeabzügen, Außenrücksprüngen und dem gesamten flachen Layout des Teils. Diese Präzision ist von entscheidender Bedeutung, da sie sicherstellt, dass die endgültigen Abmessungen des gebogenen Teils den Konstruktionsspezifikationen entsprechen und Fehler vermieden werden, die durch die Verwendung allgemeiner oder ungenauer K-Faktor-Werte entstehen könnten.

Der K-Faktor variiert in Abhängigkeit von mehreren Parametern, darunter Materialart, Dicke, Umformverfahren, Werkzeug und Biegewinkel. Diese Variabilität bedeutet, dass der K-Faktor auf die spezifischen Bedingungen des Biegeprozesses zugeschnitten werden muss. Durch die Berücksichtigung dieser Faktoren hilft der K-Faktor bei der Anpassung der Biegeausgleichsformel, um genauere Ergebnisse zu erzielen.

Schließlich ist ein korrekter Wert des K-Faktors wichtig, um Fehler in den endgültigen Abmessungen des gefalzten Blechs zu vermeiden. Falsche K-Faktor-Werte können zu Ungenauigkeiten bei den Biegezugaben führen, was zu Teilen führt, die nicht den erforderlichen Spezifikationen entsprechen. Daher ist die genaue Bestimmung und Verwendung des K-Faktors für die Herstellung hochwertiger Bauteile von entscheidender Bedeutung.

Zusammenfassend lässt sich sagen, dass der K-Faktor wichtig ist, weil er die genaue Berechnung von Biegezugaben ermöglicht, die Verschiebung der neutralen Achse berücksichtigt und die spezifischen Material- und Prozessparameter berücksichtigt, die alle wesentlich sind, um genaue und zuverlässige Ergebnisse beim Blechbiegen zu erzielen.

Was sind die gemeinsamen Variablen in der Formel für die Biegezugabe?

Die Formel für die Biegezugabe beim Biegen von Blechen umfasst in der Regel mehrere Schlüsselvariablen:

• Biegewinkel (A): Dies ist der Winkel, in dem die Biegung durchgeführt wird, und wird normalerweise in Grad gemessen. Er wird in Berechnungen oft in seiner Komplementärform verwendet.
• Innenradius (R oder Ir): Dies bezieht sich auf den Radius der Biegung auf der Innenseite des Materials. Er ist ein entscheidender Faktor bei der Bestimmung der Biegezugabe.
• Materialdicke (T oder Mt): Dies ist die Dicke des zu biegenden Blechs, die den K-Faktor und die gesamte Biegezugabe beeinflusst.
• K-Faktor (K): Dies ist der Prozentsatz der Materialdicke, bei dem keine Dehnung oder Stauchung auftritt, im Wesentlichen die neutrale Achse. Der K-Faktor variiert je nach Materialtyp und -eigenschaften.

Die Biegezugabe (BA) kann nach folgender Formel berechnet werden:

oder

wobei (0,017453) gleich (π/180) und (0,0078) gleich (π /180) x K) - Faktor ist.

Diese Variablen sind entscheidend für die genaue Bestimmung der Biegezugabe, die für die präzise Blechbearbeitung entscheidend ist.

Kann die Formel für die Biegezugabe je nach Materialart variieren?

Ja, die Formel für die Biegezugabe kann je nach Materialtyp und anderen Faktoren wie Materialstärke, Biegewinkel und spezifischem Biegeverfahren erheblich variieren.

Der K-Faktor, eine entscheidende Komponente der Formel für die Biegezugabe, stellt die Verschiebung der theoretischen neutralen Achse während des Biegens dar und variiert je nach Material. So wird für kaltgewalzten Baustahl in der Regel ein K-Faktor von 0,446 verwendet, während andere Werkstoffe wie Edelstahl und Aluminium aufgrund ihrer besonderen Eigenschaften und ihres Biegeverhaltens andere K-Faktoren aufweisen.

Die Formel für die Biegezugabe berücksichtigt auch die Materialstärke und den Biegewinkel, die von Material zu Material unterschiedlich sein können. Eine allgemeine Form der Biegezugabeformel lautet:

wo:

• ( \theta ) ist der Biegewinkel,
• ( r ) ist der Innenradius,
• ( K ) ist der K-Faktor,
• ( T ) ist die Materialdicke.

Verschiedene Materialien haben unterschiedliche Eigenschaften wie Elastizität, Zugfestigkeit und Faserrichtung, die ihr Biegeverhalten beeinflussen. So lässt sich Aluminium beispielsweise leichter biegen als Stahl, was Anpassungen bei der Berechnung der Biegezugabe erfordert. Außerdem kann das Biegen eines Metalls entlang seiner Faserrichtung mehr Kraft und eine andere Biegezugabe erfordern als das Biegen quer zur Faser.

Die Tendenz des Materials, nach dem Biegen zurückzuspringen, die so genannte Rückfederung, muss ebenfalls berücksichtigt werden. Dabei wird das Material etwas zu stark gebogen, um die elastische Rückfederung zu berücksichtigen, die vom Materialtyp und seinen Eigenschaften abhängt.

Zusammenfassend lässt sich sagen, dass die Formel für die Biegezugabe auf das jeweils verwendete Material zugeschnitten sein muss, wobei dessen einzigartige Eigenschaften, die Dicke und der jeweilige Biegeprozess zu berücksichtigen sind.