Wie stellen Ingenieure die Festigkeit und Haltbarkeit von Trägern unter verschiedenen Belastungen sicher? Dieser Artikel befasst sich mit den Grundsätzen der Biegeschubspannung und den Bedingungen, die für die Aufrechterhaltung der Trägerfestigkeit erforderlich sind. Er befasst sich mit der Spannungsverteilung in verschiedenen Trägerquerschnitten - rechteckig, kreisförmig, I-förmig und dünnwandig ringförmig - und zeigt Möglichkeiten auf, die Leistung von Trägern durch bessere Konstruktion und Materialverwendung zu verbessern. Erfahren Sie, wie Scher- und Biegespannungen zusammenwirken, und entdecken Sie praktische Tipps zur Optimierung der Trägerkonstruktion und -anwendung.
Auf den Querschnitt eines Trägers, der einer Querkraft ausgesetzt ist, wirken sowohl ein Biegemoment als auch eine Querkraft, was zu einer Normalspannung und einer Scherspannung auf den Querschnitt führt. Im Folgenden werden die Biegeschubspannungen einiger gängiger Trägerquerschnitte erörtert.
Ein kleines Segment mit der Länge dx wird unter Querkraftbiegung aus dem Balken geschnitten. Der Träger ist unbelastet, und die Querkräfte auf beiden Seiten des Segments sind gleich, aber in entgegengesetzter Richtung. Das Biegemoment am rechten Abschnitt ist größer als das am linken Abschnitt, was zu unterschiedlichen Normalspannungen in den beiden Abschnitten führt.
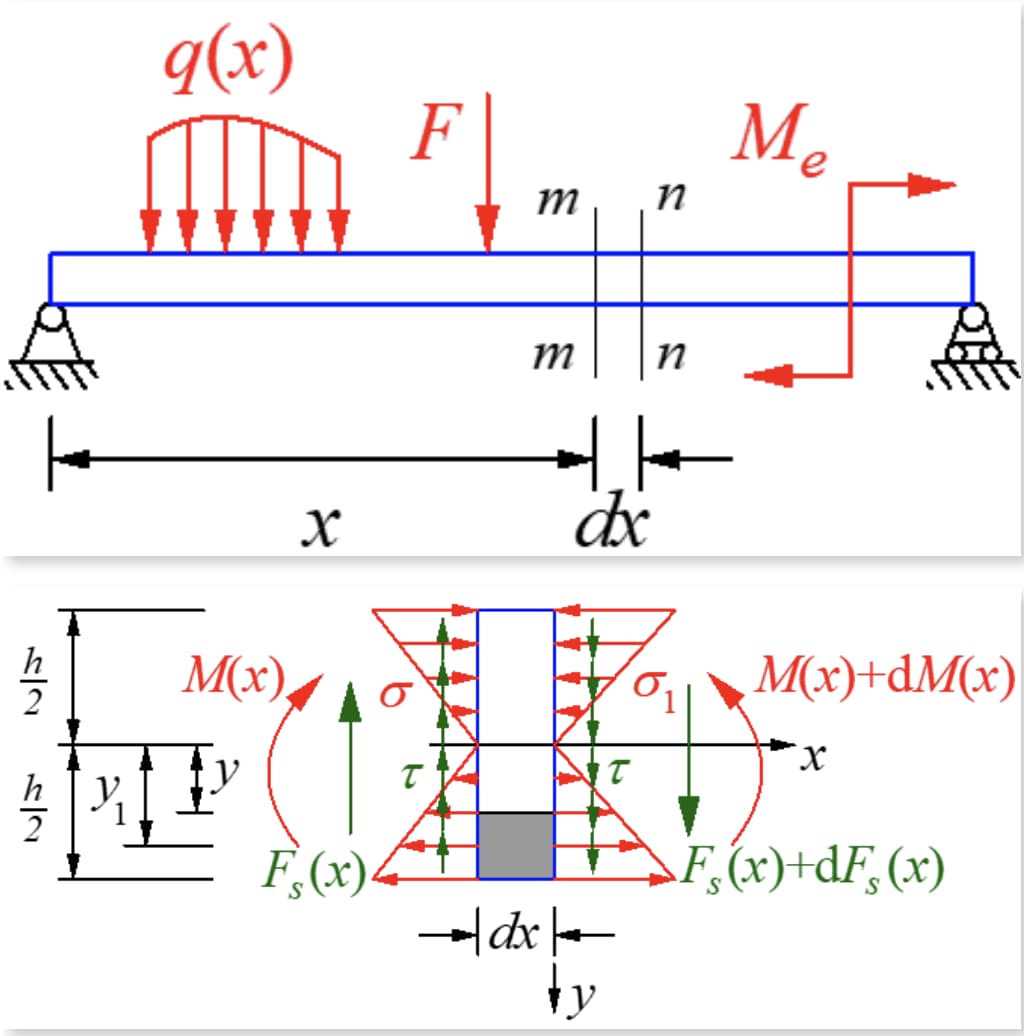
Bei einem schmalen rechteckigen Querschnitt verläuft die Schubspannung auf beiden Seiten des Trägers tangential zur Begrenzung, da es auf der Seite keine Schubspannung gibt. Da der Balken symmetrisch und parallel zur Begrenzung gebogen ist, muss die Schubspannung auf der y-Achse der Symmetrieachse in y-Richtung liegen und ändert sich nur wenig entlang der Breitenrichtung.
Daher werden die folgenden Annahmen über das Verteilungsgesetz der Schubspannung auf den Querschnitt gemacht:
Wenn das Verhältnis von Höhe zu Breite des Querschnitts größer als 2 ist, ist die auf der obigen Annahme basierende Lösung im Vergleich zur exakten Lösung aus der elastischen Theorie genau genug.
Nach dem Schubspannungs-Reziprozitäts-Theorem sollte auf dem Längsschnitt, der senkrecht zum Querschnitt verläuft, eine Schubspannung auftreten, die der Größe des Querschnitts entspricht. Schneiden Sie ein Mikrosegment entlang der Längsebene mit der momentneutralen Achse weg von y und nehmen Sie das Mikroelement auf der unteren Seite der Längsebene. Die Kräfte sind wie in der Abbildung unten dargestellt.
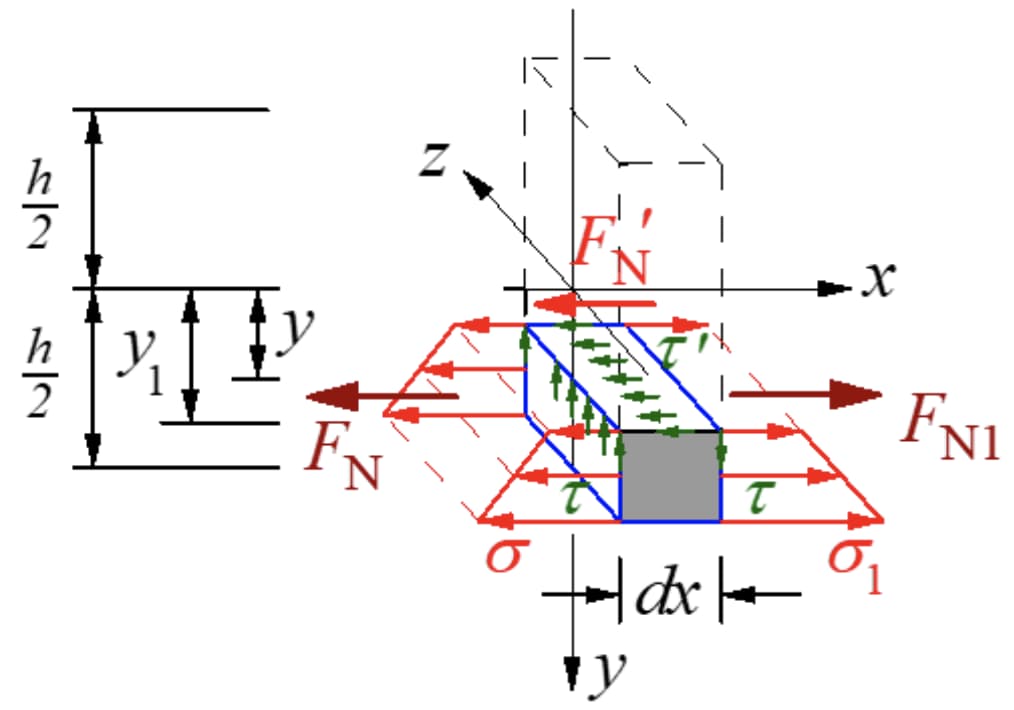
Die resultierende Kraft der Normalspannung auf den linken Abschnitt ist:
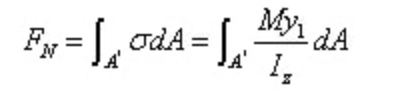
Die resultierende Kraft der Normalspannung auf den rechten Abschnitt ist：
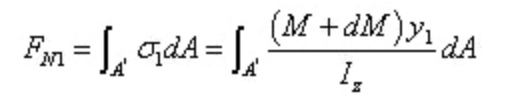
Es ist klar, dass die beiden Resultierenden unterschiedlich groß sind. Um das Gleichgewicht des Mikrosegments aufrechtzuerhalten, muss eine Kraft in axialer Richtung auf den Längsschnitt wirken. Diese Kraft ist das Ergebnis von Scherspannung, was das Vorhandensein von Scherspannung im Längsschnitt bestätigt.
Da dx ein kleiner Betrag ist, soll die Schubspannung in der Längsebene gleichmäßig verteilt sein：.
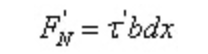
Gemäß den Gleichgewichtsbedingungen：
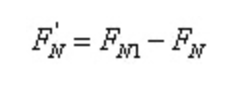
Das heißt,
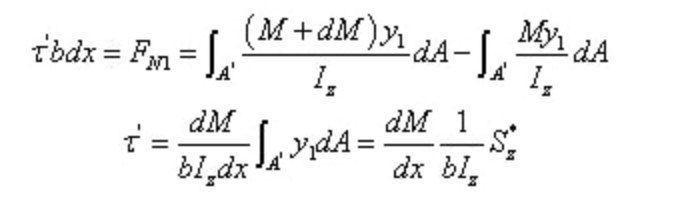
Unter,
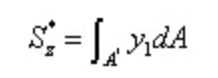
Aus dem Kehrwerttheorem der Schubspannung und dem Differentialverhältnis zwischen Querkraft und Biegemoment:
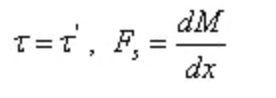
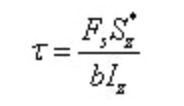
Davon:
Unter,
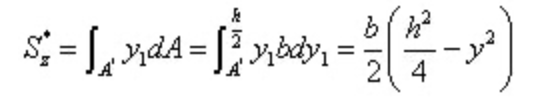
Einsetzen in die Formel zur Berechnung der Scherspannung
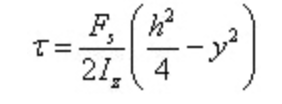
Die Scherspannung ist parabelförmig über die Querschnittshöhe verteilt.
Bei y=0 liegt die maximale Schubspannung des Querschnitts an der neutralen Achse vor
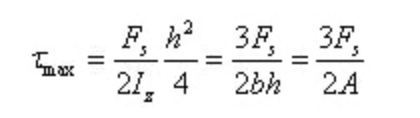
Die Winkeldehnung ist
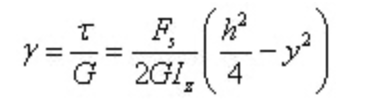
Es ist zu erkennen, dass die Winkeldehnung ebenfalls parabelförmig über die Querschnittshöhe verteilt ist.
Zu diesem Zeitpunkt ist die Verformung des Querschnitts bei der Biegung der Querkraft in der nachstehenden Abbildung dargestellt, was beweist, dass die Biegeverformung der Querkraft nicht der Annahme einer Ebene entspricht.
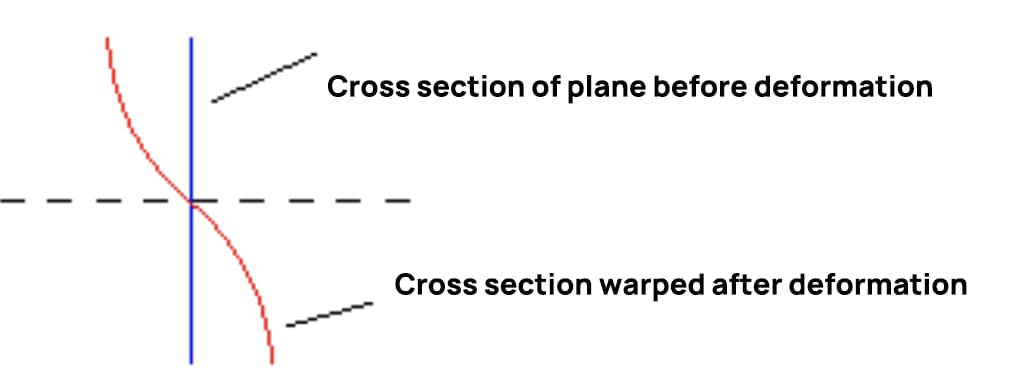
Wenn die Scherkraft konstant bleibt, ist die Scherspannung an aufeinanderfolgenden Querschnitten gleich, und der Grad der Verformung ist ebenfalls gleich. Die Länge der Längsfasern ändert sich durch die Verformung des Querschnitts nicht, so dass keine zusätzliche Normalspannung entsteht. Wenn sich die Scherkraft mit der Position des Querschnitts ändert, ist der Verformungsgrad an zwei aufeinanderfolgenden Querschnitten unterschiedlich, was zu zusätzlichen Normalspannungen auf dem Querschnitt führt.
Für symmetrische Querschnitte anderer Formen kann die ungefähre Scherspannungslösung mit der obigen Methode abgeleitet werden.
Für einen rechteckigen Querschnitt ist in der Formel zur Spannungsberechnung die Querschnittsbreite (b) konstant, und das statische Moment der halben Querschnittsfläche auf einer Seite der neutralen Achse zur neutralen Achse ist das größte. Infolgedessen ist die Schubspannung an jedem Punkt der neutralen Achse am größten.
Bei symmetrischen Querschnitten anderer Formen liegt die maximale Schubspannung im Querschnitt in der Regel an verschiedenen Punkten der neutralen Achse, mit Ausnahme von Querschnitten mit deutlich vergrößerter Breite an der neutralen Achse (z. B. Querschnitte) oder einigen Querschnitten mit variabler Breite (z. B. gleichschenklige Dreiecksprofile).
Daher wird im Folgenden bei Trägern mit I-förmigem, ringförmigem und kreisförmigem Querschnitt hauptsächlich die maximale Schubspannung an jedem Punkt der neutralen Achse erörtert.
Die Schubspannung an jedem Punkt des Randes eines kreisförmigen Querschnitts ist tangential zum Umfang, gemäß dem Satz von der reziproken Schubspannung. An jedem Punkt der Symmetrieachse muss die Schubspannung in y-Richtung liegen. Es kann davon ausgegangen werden, dass die Verteilung der Schubspannung in einem Punkt auf der Symmetrieachse für jeden Punkt entlang der Breite y von der neutralen Achse konvergiert und die Komponenten der Schubspannung entlang der Y-Richtung an jedem Punkt entlang der Breite gleich sind.
Die maximale Schubspannung des kreisförmigen Querschnitts liegt weiterhin auf der neutralen Achse, und ihre Richtung ist parallel zur äußeren Kraft, mit dem gleichen Wert an jedem Punkt der neutralen Achse.
Die maximale Scherspannung beträgt
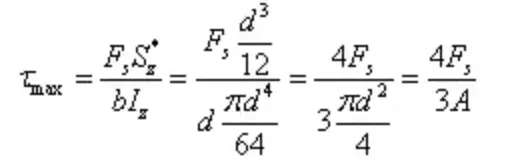
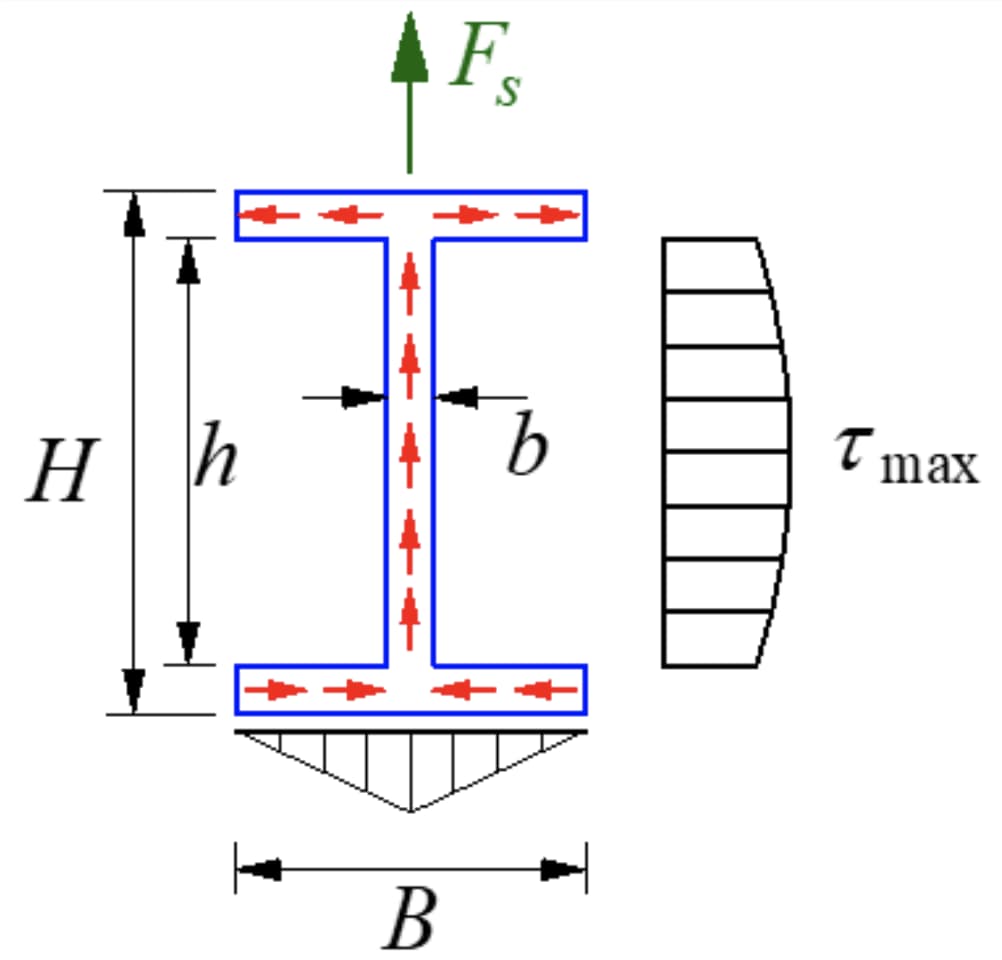
Der I-förmige Querschnitt ist ein dünnwandiger offener Querschnitt mit einer Spannungsverteilung wie in der Abbildung dargestellt. Die Größe der Schubspannung entlang der Wanddicke ist gleich, bekannt als Schubspannungsfluss, der in Scherrichtung fließt.
Die Komponente der Schubspannung parallel zur y-Achse am Flansch ist zweitrangig und vernachlässigbar, wobei der Schwerpunkt auf der Komponente parallel zur Längsseite des Flansches liegt. Die Scherspannung am Steg hat eine parabolische Verteilung, deren Größe in der Abbildung dargestellt ist.
Die maximale Schubspannung liegt in der neutralen Achse.
Im Falle von I-förmiger Stahldie maximale Scherspannung:
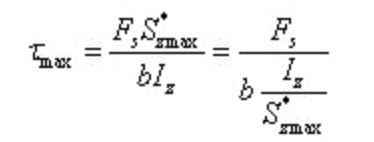
Dabei ist b die Dicke der Bahn und Iz/s*zmax kann aus der Profilstahltabelle entnommen werden.
Wenn es sich um einen I-förmigen Querschnitt handelt, der aus drei langen und schmalen Rechtecken besteht, lassen sich die maximalen und minimalen Schubspannungen am Steg wie folgt ermitteln:
Aus den beiden obigen Formeln ist ersichtlich, dass die Breite des Stegs viel kleiner ist als die Breite des Flansches, so dass sich die maximale Scherspannung am Steg nicht wesentlich von der minimalen Scherspannung unterscheidet.
Daher kann davon ausgegangen werden, dass die Scherspannung auf dem Steg ungefähr gleichmäßig verteilt ist.
Die resultierende Schubspannung auf den Steg macht 95-97% der Gesamtschubkraft aus, und die Schubkraft auf den Querschnitt wird hauptsächlich vom Steg getragen.
Da der Steg fast die gesamte Scherkraft auf den Querschnitt trägt und die Scherspannung auf dem Steg nahezu gleichmäßig verteilt ist, kann die maximale Scherspannung näherungsweise berechnet werden, indem die Scherkraft durch die Querschnittsfläche des ventralen Pols geteilt wird:
Gleichzeitig wird der gesamte Bereich der I-Träger Der Flansch ist am weitesten von der neutralen Achse entfernt, und die Normalspannung an jedem Punkt ist relativ groß, so dass der Flansch den größten Teil des Biegemoments auf den Abschnitt trägt.
Die Dicke des dünnwandigen Ringprofils ist d, der mittlere Radius des Rings ist r, und die Dicke ist weitaus geringer als der mittlere Radius, so dass man davon ausgehen kann, dass:
Die Scherspannung im Querschnitt ist entlang der Wanddicke gleich;
Die Richtung der Scherspannung verläuft tangential zur Mittellinie des Querschnitts, und die Richtung des Scherspannungsflusses verläuft entlang der Scherrichtung.
Die maximale Schubspannung liegt in der neutralen Achse:
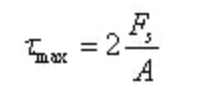
Dabei ist A die Fläche des ringförmigen Abschnitts.
Zustand der Biege-Normalspannungsfestigkeit:
Bei neutralen achsensymmetrischen Querschnitten sind die maximale Zugnormalspannung und die maximale Drucknormalspannung gleich.
Es werden häufig Kunststoffe und deren Festigkeitsbedingungen verwendet:
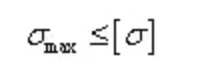
Bei einem Querschnitt mit asymmetrischer neutraler Achse sind die maximale Zugnormalspannung und die maximale Drucknormalspannung nicht gleich.
Häufig werden spröde Materialien und deren Festigkeitsbedingungen verwendet:
Die Festigkeitsbedingung der Biegeschubspannung ist:
Die Biege-Normalspannung ist der wichtigste Faktor für die Kontrolle des Trägers.
Daher ist der Festigkeitszustand der Biegenormalspannung häufig die wichtigste Grundlage für die Bemessung von Trägern.
Ausgehend vom Festigkeitszustand sollten zur Verbesserung der Tragfähigkeit des Trägers zwei Aspekte berücksichtigt werden:
Einerseits sollte die Beanspruchung des Trägers vernünftig gestaltet werden, um das maximale Biegemoment zu reduzieren;
Andererseits wird eine vernünftige Querschnittsform gewählt, um den Biegequerschnittskoeffizienten des Querschnitts zu verbessern und die Eigenschaften des Materials voll auszunutzen.
Verbessern Sie den Spannungszustand des Trägers und versuchen Sie, das maximale Biegemoment im Träger zu verringern.
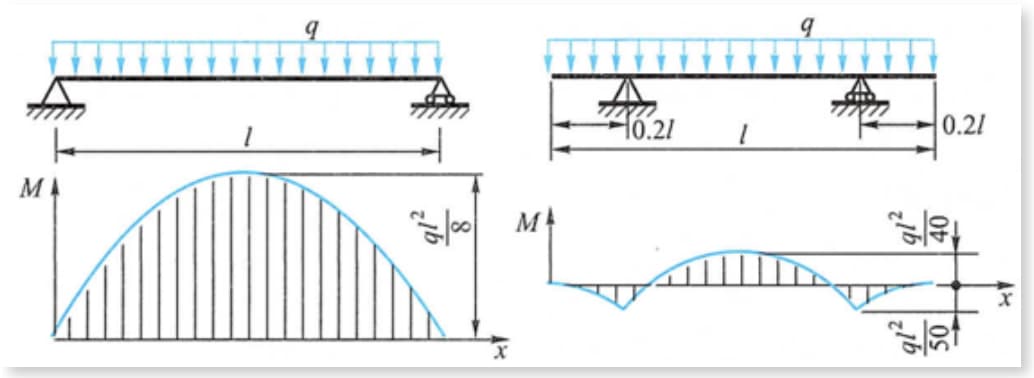
Wie in der Abbildung zu sehen ist, wird das maximale Biegemoment des Trägers bei gleichmäßiger Belastung stark reduziert, wenn die Stütze um eine bestimmte Strecke von den beiden Enden des Trägers nach innen verschoben wird.
Zum Beispiel können der Träger und der zylindrische Container eines Portalkrans, dessen Auflagepunkt leicht zur Mitte hin verschoben ist, den Effekt der Reduzierung des maximalen Biegemoments erzielen.
Je größer der Biegequerschnittskoeffizient ist, desto geringer ist die Spannung und desto höher ist die Tragfähigkeit des Trägers.
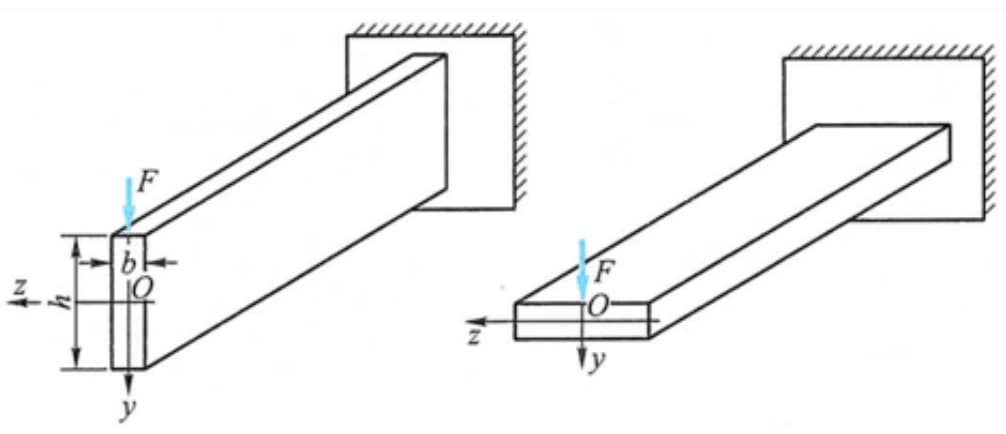
Wenn der Träger beispielsweise in vertikaler Richtung belastet wird, ist der Biegewiderstandsbeiwert größer, wenn das Profil vertikal angeordnet ist, so dass es sinnvoller ist, es vertikal als horizontal anzuordnen.
Durch die Verbesserung des Biegequerschnittskoeffizienten des Profils erhoffen wir uns auch einen geringeren Materialverbrauch, um eine bessere Wirtschaftlichkeit zu erreichen.
Daher wird das Verhältnis von Biegequerschnittskoeffizient zu Querschnittsfläche im Allgemeinen verwendet, um die Rationalität der Querschnittsgestaltung zu messen.
Bei gleicher Querschnittsfläche ist ein rechteckiger Querschnitt (Höhe größer als Breite) sinnvoller als ein kreisförmiger Querschnitt, während ein I-förmiger Querschnitt oder ein Kastenquerschnitt sinnvoller ist als ein rechteckiger Querschnitt.
Um die Materialien optimal zu nutzen, sollten sie daher so weit wie möglich von der neutralen Achse entfernt platziert werden.
Bei der Erörterung der angemessenen Form des Abschnitts ist die mechanische Eigenschaften des Materials sollte ebenfalls berücksichtigt werden.
Materialien mit gleicher Zug- und Druckfestigkeit (z. B. Stahl mit niedrigem Kohlenstoffgehalt) sollten neutrale achsensymmetrische Querschnitte aufweisen, wie z. B. kreisförmig, rechteckig, I-förmig, kastenförmig usw.
Auf diese Weise können die maximale Zugspannung und die maximale Druckspannung am oberen und unteren Rand des Profils gleich sein.
Bei Werkstoffen mit ungleicher Zug- und Druckfestigkeit (wie Gusseisen, Zement usw.) sollte die Querschnittsform mit der zur Zugseite geneigten neutralen Achse gewählt werden.
Die oben beschriebenen Träger haben alle den gleichen Querschnitt, und der Biegewiderstandsbeiwert ist konstant, aber im Allgemeinen ändert sich das Biegemoment eines jeden Trägerabschnitts mit der Position des Abschnitts.
Der Querschnitt eines geraden Trägers sollte nach dem maximalen Biegemoment bemessen werden, und seine maximale Spannung liegt in der Nähe der zulässigen Spannung.
Das Biegemoment auf andere Abschnitte ist gering, so dass die Spannung gering ist und das Material nicht vollständig ausgenutzt wird.
Um Material zu sparen und das Eigengewicht zu reduzieren, kann die Querschnittsgröße so verändert werden, dass sich der Biegequerschnittskoeffizient mit dem Biegemoment ändert.
Ein größerer Querschnitt wird verwendet, wenn das Biegemoment größer ist, während ein kleinerer Querschnitt verwendet wird, wenn das Biegemoment kleiner ist.
Diese Art von Balken, deren Querschnitt sich entlang der Achse ändert, wird als Balken mit variablem Querschnitt bezeichnet.
Wenn die maximale Normalspannung auf jedem Querschnitt eines Trägers mit variablem Querschnitt gleich ist und der zulässigen Spannung entspricht, wird er als gleichfester Träger bezeichnet.
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
AR 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO