1. Konzept:
Stützt seitliche Lasten wie Bodenbalken, Kranbalken, Pfetten, Brücken usw.
2. Klassifizierung:
(1) Feste Bahn：
H-förmiges Stahlprofil: Leicht zu verarbeiten, einfach in der Herstellung und kostengünstig.
Zusammengesetzter Abschnitt: Wenn der H-förmige Stahl nicht den Anforderungen der Festigkeit und Steifigkeit.
(2) Gitterstruktur:
Bei einer Spannweite von mehr als 40 m ist es am besten, einen Fachwerkbinder zu verwenden.
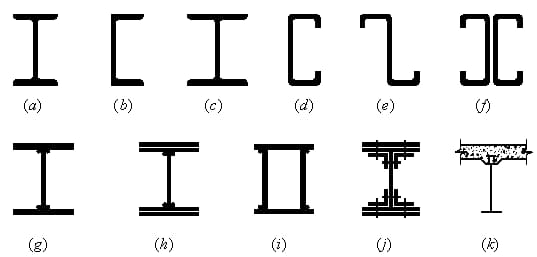
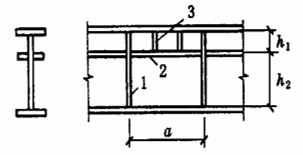
3. Balkengitter:
Ein flächiges System, das aus Haupt- und Nebenträgern besteht, die sich vertikal und horizontal kreuzen.
(1) Vereinfachtes Strahlenraster: Einzelner Fernlichtstrahl.
(2) Gewöhnlicher Balkenrost: Aufgeteilt in Haupt- und Nebenträger.
(3) Verbundträgerraster: Aufgeteilt in Hauptträger, horizontale und vertikale Nebenträger.
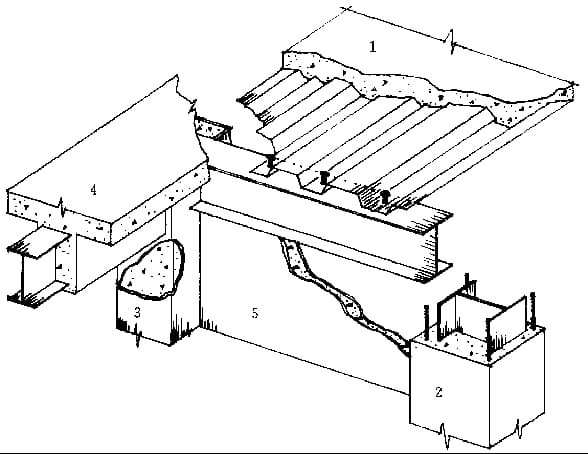
4. Interaktion zwischen Trägern und Platten:
(1) Co-working: Bodenplatte aus Verbundwerkstoff.
(2) Nicht-kooperative Arbeiten: Allgemeine Stahlbetonplatte.
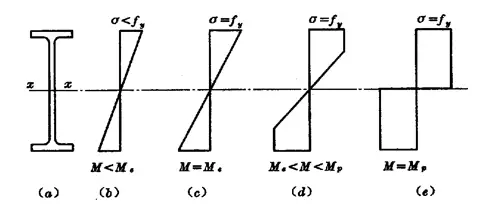
Die Entwicklung der Normalspannung im Querschnitt kann in drei Phasen unterteilt werden:
(1) Elastische Phase: Bei dynamischer Belastung.
(2) Elastisch-plastisches Stadium: Bei statischer Belastung oder indirekter dynamischer Belastung.
(3) Kunststoffbühne:
Biegefähigkeit während der elastisch-plastischen Phase eines Querschnitts:
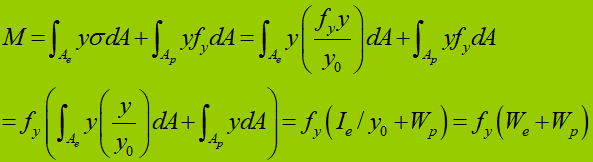
Für einen rechteckigen Querschnitt:
(1) Elastische Phase:
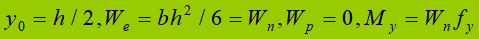
(2) Kunststoffbühne:
(3) Elastisch-plastisches Stadium:
Querschnittsformfaktor:
Plastische Entwicklung eines Teilquerschnitts (1/4 Querschnitt, a = h/8) als Grenzzustand:
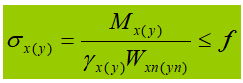
In der Formel:
γ ist der Teilsicherheitsbeiwert für das Moment, der anhand von Tabelle 5.1 in Abschnitt 5 des Bemessungscodes ermittelt werden kann.
Es gibt zwei Fälle, in denen der Teilsicherheitsbeiwert für das Moment mit 1,0 angesetzt werden sollte.
Methode:
S:
Die Scherfestigkeit kann mit Hilfe der Scherflusstheorie berechnet werden, wobei davon ausgegangen wird, dass sie gleichmäßig entlang der Dickenrichtung der dünnen Wand verteilt ist.
(1) Bei der Berechnung der vertikalen Schubspannung an einem beliebigen Punkt des Stegs ist es erforderlich, das Flächenträgheitsmoment des Bruttoquerschnitts über oder unter diesem Punkt in Bezug auf die neutrale Achse x zu berechnen.
(2) Bei der Berechnung der horizontalen Schubspannung an einem beliebigen Punkt des Flansches ist es erforderlich, das Flächenträgheitsmoment des Bruttoquerschnitts links oder rechts von diesem Punkt in Bezug auf die neutrale Achse x zu berechnen.
Wo tw ist die Dicke des Querschnitts an der Stelle, an der die Scherspannung berechnet wird.
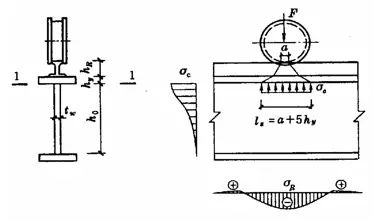
Wenn der Flansch eines Trägers einer großen festen Mittellast (einschließlich Auflagerreaktionen) ausgesetzt ist und keine Versteifungen gemäß Abbildung 5-5 (a) vorgesehen sind, oder wenn er einer beweglichen Einzellast (z. B. Kranraddruck) gemäß Abbildung 5-5 (b) ausgesetzt ist, sollte die lokale Druckfestigkeit am Rand der Steghöhe berechnet werden. Unter der Annahme, dass sich die Einzellast vom Angriffspunkt aus über einen Höhenbereich von hy im Verhältnis 1:2,5 und streut im Verhältnis 1:1 in einem Höhenbereich von hRgleichmäßig über die Höhe der Bahn verteilt ist Kantenberechnung. Die resultierende σc liegt sehr nahe am maximalen theoretischen lokalen Druck. Die lokale Druckfestigkeit kann mit der folgenden Formel berechnet werden:
In der Formel,
Wenn die Berechnung nicht zufriedenstellend ist, kann die feste Einzellast oder das Auflager durch das Anbringen von Querversteifungen oder die Änderung der Querschnittsgröße verstärkt werden. Bei beweglichen Einzellasten kann jedoch nur die Querschnittsgröße geändert werden.
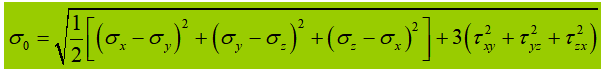
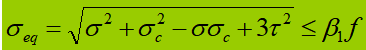
Wenn der Bauchrüttler in der berechneten Höhe erheblichen Normalspannungen, Scherspannungen oder lokalen Druckspannungen ausgesetzt ist, muss die Vergleichsspannung an dieser Stelle berechnet werden.
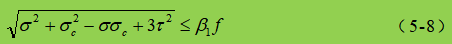
In der Formel:
σ, τ, σc - Biege-Normalspannung, Scherspannung und lokale Druckspannung an der gleichen Stelle der Berechnungshöhe der Bauchplatte, positiv für Zugspannung und negativ für Druckspannung;
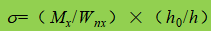
β1 - Koeffizient für die Erhöhung des Bemessungswertes der Druckfestigkeit an einem lokalen Punkt. Wenn σ und σc das gleiche Vorzeichen haben oder σc=0, β1=1,1; wenn σ und σc entgegengesetzte Vorzeichen haben, β1=1.2.
Allgemeines Phänomen der Instabilität:
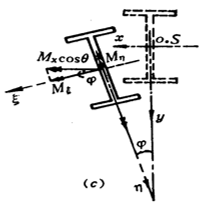
Analyse des Mechanismus:
Nachdem der Träger durch Biegung verformt wurde, wird der obere Flansch auf Druck beansprucht. Aufgrund der unzureichenden seitlichen Steifigkeit des Trägers kommt es zu einer seitlichen Knickverformung des Trägers. Die Biegeverformung in der Ebene, die durch das Moment verursacht wird, tritt zusammen mit einer Torsionsverformung auf, die durch die ungleiche Biegung von der Ober- zur Unterseite des Trägerprofils verursacht wird.
Daher nimmt die Gesamtinstabilität des Trägers die Form des Biegedrillknickens oder, genauer gesagt, des Biege- und Torsionsknickens an.
(1) C1, C2, C3 - bezogen auf die Lastart
(2) Iy, Iw, It - Trägheitsmoment des Querschnitts
(3) L - Unverspannte Länge in Querrichtung
(4) a - Lage des Angriffspunkts in Höhenrichtung.
(5) 
| Zustand der Belastung | Koeffizient | ||
| G | C2 | G | |
| Mittlere Spannweite - Einzellast | 1.35 | 0.55 | 0.41 |
| Gleichmäßig verteilte Last über die gesamte Spannweite | 1.13 | 0.46 | 0.53 |
| Reines Biegen | 1.00 | 0.00 | 1.00 |
Die wichtigsten Faktoren, die die Gesamtstabilität von Stahlträgern beeinflussen, sind:
(1) Die unverspannte Länge in Querrichtung oder der Abstand L1 zwischen dem seitlichen Auflagerpunkt des Druckflansches. Je kleiner der Wert von L1 ist, desto besser ist die Gesamtstabilität des Trägers und desto höher ist das kritische Biegemoment.
(2) Die Größe des Querschnitts, einschließlich verschiedener Trägheitsmomente. Je größer das Trägheitsmoment ist, desto besser ist die Gesamtstabilität des Trägers. Insbesondere kann eine Vergrößerung der Breite des Druckflansches b1 auch den Wert von βy in der Formel erhöhen.
(3) Die Begrenzungen des Querschnitts durch die Endstützen des Trägers. Wenn die Zwänge für die Drehung des Querschnitts um die y-Achse verbessert werden können, wird die Gesamtstabilität des Trägers erheblich verbessert.
(4) Belastungsart: Reine Biegung, gleichmäßig verteilte Last, konzentrierte Last in der Mitte der Spannweite.
(5) Die Lage des Angriffspunktes der Last in Höhenrichtung des Querschnitts, ein Wert, der für den oberen Flansch negativ und für den unteren Flansch positiv ist.
Biegen in einer Ebene:
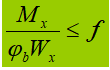
1. Geschweißter I-förmiger Querschnitt, biaxialsymmetrisch, rein Biegebelastung.
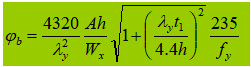
2. Geschweißter I-förmiger Querschnitt, einachsig symmetrisch (Auswirkungen von asymmetrischem Querschnitt und unterschiedlichen Belastungen)
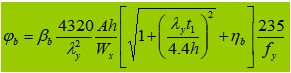
Wenn φb>0,6 ist, wird der Stabilitätskoeffizient wie folgt berechnet:
3. Gewalzter gewöhnlicher I-förmiger Stahlträger mit einfacher Unterstützung.
4. Warmgewalzter, einfach gestützter Träger aus Kanalstahl.
5. Ein doppelachsensymmetrischer I-förmiger Auslegerbalken.
Der komprimierte Flansch des Trägers ist mit einer Deckschicht (Stahlbeton oder Stahlplatte) und fest verbunden, um eine seitliche Verschiebung des Druckflansches zu verhindern.
Bei einfach gestützten H-Trägern oder I-Trägern darf das Verhältnis der freien Länge L1 zur Breite b des Stauchflansches den in Tabelle 5.4 angegebenen Wert nicht überschreiten.
Tabelle 5.4: Maximaler Wert von L1/b1, für den keine Gesamtstabilitätsberechnung für einfach gestützte H-Träger oder I-Träger erforderlich ist.
| Stahlsorte | Ein Träger ohne seitliche Stützpunkte in der Mitte der Spannweite. | Ein Träger mit einem Flansch, der über die gesamte Spannweite auf Druck beansprucht wird, und mit seitlichen Auflagepunkten, unabhängig davon, wo die Last aufgebracht wird. | |
| Die Last wird auf den Flansch aufgebracht. | Die Last wird auf den unteren Flansch aufgebracht. | ||
| Q235 | 13.0 | 20.0 | 16.0 |
| Q345 | 10.5 | 16.5 | 13.0 |
| Q39 | 10.0 | 15.5 | 12.5 |
| Q420 | 9.5 | 15.0 | 12.0 |
1. Bestimmen Sie, ob ein Gesamtstabilitätsnachweis erforderlich ist.
2. Berechnen Sie die Querschnittsparameter.
3. den äquivalenten kritischen Biegemomentkoeffizienten βb entsprechend den Belastungsbedingungen zu ermitteln.
4. Setzen Sie die Werte in die Formeln ein, um den Gesamtstabilitätskoeffizienten ϕb zu erhalten, und überprüfen Sie die Gesamtstabilität.
Beispiel: 5-2，5-3
Flanschplatte: Die Belastung ist relativ einfach, und die lokale Stabilität wird durch eine Begrenzung des Verhältnisses von Breite zu Dicke der Platte gewährleistet.
Web-Platte: Die Belastung ist komplex, und um die Festigkeitsanforderungen zu erfüllen, ist die Querschnittshöhe oft groß. Wenn wir das Verhältnis von Höhe zu Dicke des Stegblechs weiterhin begrenzen, wird der Wert des Stegblechs sehr groß, was unwirtschaftlich ist. Daher werden in der Regel Versteifungen verwendet, um die Größe des Blechs zu verringern und die Tragfähigkeit der lokalen Stabilität zu verbessern.
1. Querversteifungen
2. Längsversteifungen
3. Kurze Versteifungen
Konstruktionsprinzip: Prinzip der gleichen Stärke.
Bei der elastischen Auslegung (mit γ=1,0 für die Nichtberücksichtigung der plastischen Entwicklung) wird aufgrund des Einflusses der Eigenspannunghat der tatsächliche Querschnitt das elastisch-plastische Stadium erreicht. Die "Spezifikation" nimmt Et=0.7E.
Wenn die plastische Entwicklung berücksichtigt wird (γ > 1,0), ist die plastische Entwicklung größer, und Et=0.5E.
| Nein. | Der Zustand des Stegblechs. | Spezifikationen der Versteifungsanordnung | |
| 1 |  | στ=0 | Die Versteifungen können weggelassen werden. |
| 2 | στ≠0 | Es wird empfohlen, Querversteifungen einzubauen, die den statischen und rechnerischen Anforderungen entsprechen. | |
| 3 |  | Es wird empfohlen, Querversteifungen einzubauen, die den statischen und rechnerischen Anforderungen entsprechen. | |
| 4 |  Der zusammengepresste Flansch ist gegen Verdrehen gesichert. | In der Druckzone des Querschnitts, in der die Biegespannung hoch ist, sollten Längsversteifungen angebracht werden, die den statischen und rechnerischen Anforderungen entsprechen. | |
| 5 |  Der zusammengepresste Flansch kann sich frei verdrehen. | ||
| 6 | Wenn für Berechnungszwecke erforderlich. | ||
| 7 | Wenn die lokale Druckspannung hoch ist. | Erforderlichenfalls sind in der Druckzone kurze Versteifungen anzuordnen, um den statischen und rechnerischen Erfordernissen zu entsprechen. | |
| 8 | An der Balkenauflage | Es ist ratsam, Stützstreben einzubauen, die den statischen und rechnerischen Anforderungen entsprechen. | |
| 9 | Wenn der Flansch einer großen festen Einzellast ausgesetzt ist. | ||
| 10 | In jedem Fall |  | |
1. Beulen von gespannten Verbundplatten
Es wird nur das Stegblech mit Quersteifen konfiguriert.
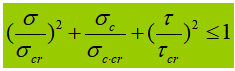
Das Stegblech ist gleichzeitig mit Quer- und Längsversteifungen ausgestattet.
(1) Zwischen Pressflansch und Längsaussteifungen.
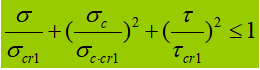
(2) Zwischen Zugflansch und Längsaussteifungen.
Kurze Quersteifen werden zwischen dem Pressflansch und den Längssteifen eingebaut.
2. Konstruktionsanforderungen an Steifen für Stegbleche
(1) Quersteifen aus Stahl, die paarweise auf beiden Seiten des Stegblechs angeordnet sind.
Nach außen vorspringende Breite:
Die Dicke:
(2) Querversteifungen aus Stahl, die auf einer Seite des Stegblechs angeordnet sind.
Nach außen ragende Breite: sollte größer sein als das 1,2-fache des nach der obigen Formel berechneten Wertes.
Dicke: sollte nicht weniger als 1/15 der nach außen ragenden Breite betragen.
(3) Bei Stegblechen, die sowohl mit Quer- als auch mit Längssteifen verstärkt sind, sollten die Längssteifen an ihren Kreuzungspunkten unterbrochen werden, während die Quersteifen durchgehend bleiben.
Das Trägheitsmoment um die z-Achse sollte ebenfalls genügen:
(4) Behandlung der Enden von Quersteifen:
3. Versteifungen zur Unterstützung
(1) Stabilitätsberechnung:
Die Stabilität der Steifen für die Abstützung wird als Druckstab berechnet, der festen Einzellasten oder Trägerauflagerreaktionen entlang seiner Achse ausgesetzt ist. Die Querschnittsfläche A dieses Druckstabs umfasst sowohl die Versteifung als auch die Stegplatte innerhalb von 15tw auf jeder Seite der Versteifung. Die Berechnungslänge wird annähernd als h0 angenommen.
(2) Berechnung der Druckfestigkeit:
Das Ende der Stützsteifen für den Träger sollte entsprechend der festen konzentrierten Last oder der Stützreaktion, die sie tragen, berechnet werden. Wenn das Ende der Steifen flach und straff geschnitten ist, sollte die Druckspannung an der Endfläche wie folgt berechnet werden:
wo:
Entwurfsschritte für Stegblech-Quersteifen:
1. Stellen Sie fest, ob Querträger installiert werden müssen;
2. Bringen Sie die Querbalken an und bestimmen Sie die Abstände a, bs, ts;
3. Überprüfen Sie den Verbundspannungszustand des Stegblechs;
4. Überprüfung der tragenden Versteifung: einschließlich der Schweißnaht (Verbindung zwischen den Querstäben und dem Stegblech), Überprüfung der axialen Druckstabilität (Stabilisierung außerhalb der z-Achsenebene) und Überprüfung der Festigkeit.
Beispiel 5-3: Prüfen Sie auf der Grundlage der Bedingungen und Ergebnisse in Beispiel 5-2, ob der in Abbildung 5-9(b) dargestellte Hauptträgerabschnitt die Anforderungen erfüllt. Der Hauptträger ist ein einfach gestützter Träger an beiden Enden, der aus Q235-Stahl hergestellt und mit Handschweißelektroden der Serie E43 geschweißt wurde.
Lösung:
1. Tragfähigkeit des Hauptträgers:
Das vereinfachte Berechnungsdiagramm für den Hauptträger ist in Abbildung 5-9(a) dargestellt. Der von den Nebenträgern auf beiden Seiten auf den Hauptträger ausgeübte Druck beträgt 2×73,69+2×2,33=152,04 kN, und der Druck der Nebenträger am Ende des Trägers ist halb so groß wie der des mittleren Nebenträgers.
Die Auflagerreaktion des Hauptträgers beträgt R=2×152,04=304,08 kN.
Das maximale Biegemoment des Trägers beträgt M=(304,08-76,02)x5-152,04×2,5=760,2 kN.m
2. Berechnen Sie die Querschnittsmerkmale:
A=131,2 cm², Ix=145449 cm⁴, Wx=3513,3 cm³. Das Eigengewicht des Hauptträgers beträgt 131,2×10²x7850x10-⁶x1,2=123,6 kg/m=1,211 kN/m. Der Faktor 1,2 soll den erhöhten Beiwert der Hauptträgeraussteifung berücksichtigen. Der Bemessungswert des Biegemoments nach Berücksichtigung des Gewichts des Hauptträgers ist M=760,2+1,2×1,211×10²/8=760,2+18,2=778,4 kN-m.
Der Bemessungswert der Reaktionskraft auf die Stütze nach Berücksichtigung des Eigengewichts des Hauptträgers beträgt R=304,08+1,2×1,211×10/2=304,08+7,27=311,3kN.
3. Stärkeprüfung
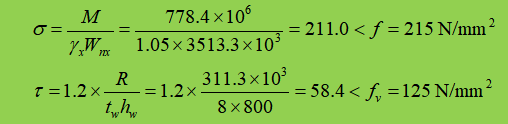
Am Anschluss des Nebenträgers sind stützende Versteifungen vorgesehen, und es treten keine lokalen Druckspannungen auf. Da die Scherspannung relativ gering ist, ist es nicht erforderlich, andere in den Querschnitt umgewandelte Spannungen nachzuweisen.
4. Auf dem Nebenträger befindet sich eine starre Platte, die die Stabilität des Nebenträgers gewährleistet und als seitlicher Stützpunkt für den Hauptträger dienen kann.
Zu diesem Zeitpunkt, da l1/b1=2500/240=10,4<16, kann die Gesamtstabilität ohne Berechnung gewährleistet werden.
5. Prüfung der Steifigkeit
Der gesamte Standardwert der vom Nebenträger übertragenen Last ist FT=(15.5+0.52)×7.5=120.2kN, therefore,
Der gesamte Standardwert der vom Nebenträger übertragenen Last ist FQ=2.5×4.2×7.5=78.75kN, therefore,
6. Lokale Stabilität
Flansch: b/t=(120-4)/14=8,3<13, was der Anforderung der örtlichen Stabilität entspricht, und γx kann mit 1,05 angenommen werden; Stegplatte: h0/tw=800/8=100, es sind Quersteifen vorzusehen, Details entfallen.
Nach dem Ausbeulen des dünnen Blechs entstehen in der Mitte des Blechs Querzugspannungen, die die Biegeverformung des Blechs in Längsrichtung weiter einschränken, so dass es dem erhöhten Druck weiterhin standhalten kann.
1. Schertragfähigkeit nach dem Knicken: Formel (5-94)
2. Die Querkrafttragfähigkeit umfasst zwei Teile: Knick-Querkraft (Knickfestigkeit) + Zugfeld-Querkraft (Festigkeit nach dem Knicken).
3. Scherkraft im Spannungsfeld:
(1) Spannungsfeldmethode (komplex);
(2) Code-Spezifikation.
Da die Biegetragfähigkeit des Stegblechs nach dem Beulen leicht abnimmt.
Zwei Annahmen:
(1) Effektive Höhe;
(2) Symmetrie zwischen der Zugzone und der Druckzone.
Die Formel zur Berechnung der Tragfähigkeit:
In der Formel,
Dies zeigt, dass:
(1) Wenn M auf dem Abschnitt kleiner ist als Mf die der Flansch aushalten kann, kann das Stegblech die Querkraft Vu aufnehmen;
(2) Wenn V auf der Strecke weniger als 0,5Vu beträgt, gilt M = Meu.
(1) Wenn die Stützsteifen allein die Gleichung (5.99) nicht erfüllen können, sollten auf beiden Seiten des Stegs gepaarte Quersteifen hinzugefügt werden, um die Länge des Knickbereichs zu verringern.
(2) Die Querschnittsabmessungen der Quersteifen sollten den Konstruktionsanforderungen für die Stegsteifen gemäß Gleichung 5.85 entsprechen.
(3) Gemäß den Spezifikationen für Stahlkonstruktionen sollte die zentrale Querversteifung als axiales Druckelement behandelt werden, und ihre Stabilität außerhalb der Ebene des Stegs sollte auf der Grundlage der Axialkraft unter Verwendung der folgenden Formel berechnet werden:
Wenn die Versteifung einer konzentrierten Querlast F ausgesetzt ist, sollte Ns um F erhöht werden.
Berechnen Sie den Bemessungswert für das maximale Biegemoment Mmax für den Balken auf der Grundlage der tatsächlichen Bedingungen.
Bestimmen Sie das erforderliche Widerstandsmoment anhand der Biegefestigkeit und der Gesamtstabilität:
Bestimmen Sie den Stahlquerschnitt anhand der Querschnittstabellen.
Überprüfung des Abschnitts:
(1) Festigkeitsnachweis: Biegung, Scherung, lokale Kompression und Vergleichsspannung.
(2) Überprüfung der Steifigkeit: Überprüfung des Verhältnisses zwischen Durchbiegung und Spannweite des Trägers.
(3) Überprüfung der Gesamtstabilität (die lokale Stabilität des Stahlprofils muss in der Regel nicht überprüft werden).
(4) Passen Sie den Abschnitt auf der Grundlage der Prüfergebnisse an und führen Sie die Prüfung erneut durch, bis er den Entwurfsanforderungen entspricht.
1) Bestimmen Sie das erforderliche Widerstandsmoment auf der Grundlage der Lastbedingungen.
2) Bestimmen Sie die Strahlhöhe:
Ausgewählte Höhe: hmin ≤ h ≤ hmax.
3). Bestimmen Sie dann die Dicke des Stegs (unter der Annahme, dass alle Querkräfte vom Steg aufgenommen werden):
Alternativ kann die Bahndicke auch mit Hilfe empirischer Formeln bestimmt werden:
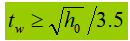
4). Bestimmen Sie die Flanschbreite:
Nach der Bestimmung der Stegdicke ergibt sich die Flanschfläche Af kann anhand der Anforderungen an die Biegefestigkeit bestimmt werden. Nehmen wir ein I-förmiges Profil als Beispiel:
Sobald Af bestimmt ist, kann entweder b oder t gewählt werden, um den anderen Wert zu bestimmen.
5). Überprüfung des Abschnitts:
6). Berechnung der Schweißnähte zwischen Steg und Flansch
Die Verbindungsschweißung wird hauptsächlich verwendet, um die Biegeschubund die Scherung pro Längeneinheit ist:
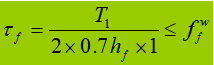
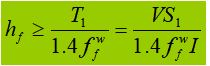
Wenn der Träger einer festen Einzellast ohne Stützversteifungen ausgesetzt ist, trägt die obere Flanschschweißnaht sowohl die Querkraft T1 und der konzentrierten Kraft F. Die von F erzeugte Kraft pro Längeneinheit ist V1:
Zweck: Zur Einsparung von Stahl und zur Bewältigung von Biegemomentänderungen.
Methoden der Abschnittsänderung:
Zu beachtende Punkte:
1. Klassifizierung: Spleißen im Werk und Spleißen vor Ort.
2. Gewalzte Stahlprofile: Stumpfschweißen und Verbinden Blechschweißen.
3. Beim Verbinden von Verbundträgern: Der Steg und die Flansche werden beim Spleißen im Werk versetzt angeordnet. Beim Verbinden auf der Baustelle werden Steg und Flansche auf demselben Abschnitt verbunden.
Zu beachtende Punkte:
1. Verbindung von primären und sekundären Stahlträgern: Überlappung und Stumpfstoß.
2. Trägerstützen:
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
ES 
RU 