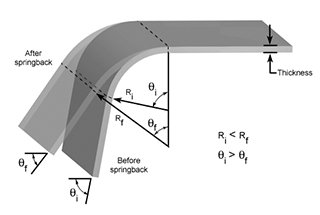
Haben Sie sich jemals gefragt, warum manche Metallteile nach dem Biegen zurückfedern? In diesem Artikel erkunden wir die faszinierende Welt der Biegestempel und erfahren, wie man die Rückfederung genau vorhersagen kann. Sie erhalten praktische Tipps und Formeln, um bei Ihren Metallbearbeitungsprojekten präzise Ergebnisse zu erzielen.
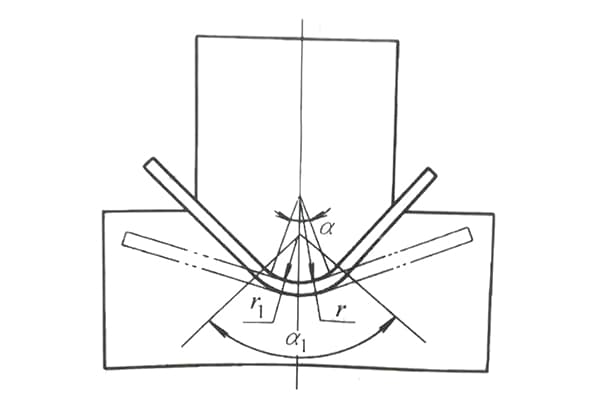
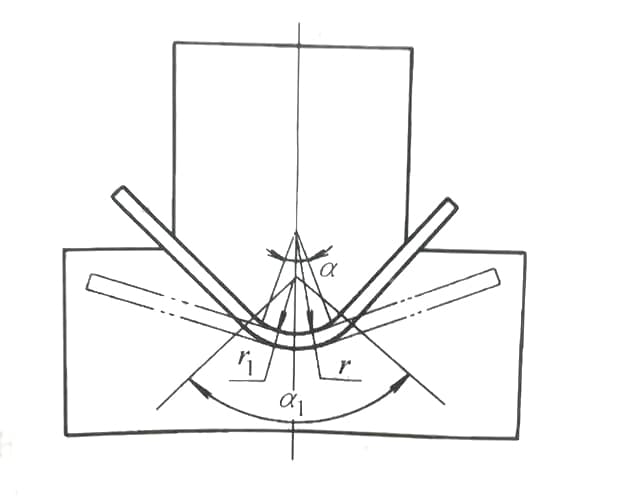
Bei der Konstruktion einer Biegematrize mit Innenbogen sind Präzision und Materialverhalten kritische Faktoren, die bei herkömmlichen Ansätzen oft übersehen werden. Viele Konstrukteure vernachlässigen die Rückfederung entweder ganz, indem sie den gleichen Radius (R) wie das fertige Produkt verwenden, oder sie wenden einen rudimentären Reduktionsfaktor auf den R-Wert an, ohne die Komplexität der Materialeigenschaften und Geometrien zu berücksichtigen.
Eine gängige Praxis für ein Produkt mit einem ursprünglichen R-Wert von 1 mm besteht beispielsweise darin, den konvexen Formradius um den Faktor 0,8 für härtere Materialien oder 0,9 für weichere Materialien zu verringern. Dieser einfache Ansatz ist zwar manchmal für einfache Anwendungen geeignet, lässt aber die für anspruchsvollere Spezifikationen erforderlichen Nuancen vermissen.
Die Grenzen dieser Methode werden besonders deutlich, wenn es um dünne Materialien und große Radien geht. Nehmen wir ein Produkt mit einer Dicke von 0,5 mm und einem Innenradius von 200 mm. In solchen Fällen wird die genaue Vorhersage der Rückfederung aufgrund des komplexen Zusammenspiels zwischen Materialeigenschaften, Verhältnis von Dicke zu Radius und Biegewinkel zu einer Herausforderung.
Um diese Einschränkungen zu beseitigen und die Präzision bei der Konstruktion von Werkzeugen zu verbessern, ist ein ausgefeilterer Ansatz erforderlich. Im folgenden Abschnitt wird eine universelle Rückfederungsformel vorgestellt, die verschiedene Material- und Geometrieparameter berücksichtigt und genauere Berechnungen auf der Grundlage numerischer Eingaben ermöglicht. Diese Methode bietet eine solide Grundlage für die Konstruktion von Werkzeugen für eine Vielzahl von Anwendungen und Materialien.
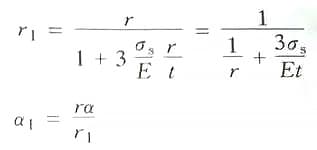
In der Formel:
Unter der Annahme von 3σs/E=A als Vereinfachungskoeffizient, dessen Werte in Tabelle 2-27 aufgeführt sind. Die Berechnungsformel für den konvexen Matrizeneckenradius beim Biegen von Stäben mit rundem Querschnitt lautet wie folgt:

Der Wert von A ist in der nachstehenden Tabelle angegeben.
| Materialwissenschaft | Staat | A | Materialwissenschaft | Staat | A |
| 1035(L4) 8A06(L6) | Glühen | 0.0012 | QBe2 | weich | 0.0064 |
| Kalte Härte | 0.0041 | hart | 0.0265 | ||
| 2A11(LY11) | weich | 0.0064 | QA15 | hart | 0.0047 |
| hart | 0.0175 | 08, 10, Q215 | 0.0032 | ||
| 2A12(LY12) | weich | 0.007 | 20, Q235 | 0.005 | |
| hart | 0.026 | 30, 35, Q255 | 0.0068 | ||
| T1, T2, T3 | weich | 0.0019 | 50 | 0.015 | |
| hart | 0.0088 | T8 | Glühen | 0.0076 | |
| H62 | weich | 0.0033 | Kalthärte | ||
| halbhart | 0.008 | ICr18N9Ti | Glühen | 0.0044 | |
| hart | 0.015 | Kalthärte | 0.018 | ||
| H68 | weich | 0.0026 | 65Mn | Glühen | 0.0076 |
| hart | 0.0148 | Kalthärte | 0.015 | ||
| QSn6,5-0,1 | hart | 0.015 | 60Si2MnA | Glühen | 0.125 |
Wenn die erforderlichen Materialien nicht verfügbar sind, können Sie auch in der folgenden Tabelle nachsehen, um die Elastizitätsmodul und die Streckgrenze des Materials und setzen Sie diese dann zur Berechnung in die obige Formel ein.
| Name des Materials | Materialqualität | Material Status | Ultimative Stärke | Dehnungsgeschwindigkeit(%) | Streckgrenze/MPa | ElastizitätsmodulE/MPa | |
| Scherwiderstand/MPa | Zugkraft/MPa | ||||||
| Kohlenstoffbaustahl | 30 | Normalisiert | 440-580 | 550-730 | 14 | 308 | 22000 |
| 55 | 550 | ≥670 | 14 | 390 | – | ||
| 60 | 550 | ≥700 | 13 | 410 | 208000 | ||
| 65 | 600 | ≥730 | 12 | 420 | – | ||
| 70 | 600 | ≥760 | 11 | 430 | 210000 | ||
| Kohlenstoffbaustahl | T7~T12 T7A-T12A | Geglüht | 600 | 750 | 10 | – | – |
| T8A | Kaltgehärtet | 600-950 | 750-1200 | – | – | – | |
| Hochwertiger Kohlenstoffstahl | 10Mn2 | Geglüht | 320-460 | 400-580 | 22 | 230 | 211000 |
| 65M | 600 | 750 | 18 | 400 | 211000 | ||
| Legierter Baustahl | 25CrMnSiA 25CrMnSi | Bei niedriger Temperatur geglüht | 400-560 | 500-700 | 18 | 950 | – |
| 30CrMnSiA 30CrMnSi | 440-600 | 550-750 | 16 | 1450850 | – | ||
| Hochwertiger Federstahl | 60Si2Mn 60Si2MnA 65Si2WA | Bei niedriger Temperatur geglüht | 720 | 900 | 10 | 1200 | 200000 |
| Kaltgehärtet | 640-960 | 800-1200 | 10 | 14001600 | – | ||
| Rostfreier Stahl | 1Cr13 | Geglüht | 320-380 | 400-170 | 21 | 420 | 210000 |
| 2Cr13 | 320-400 | 400~500 | 20 | 450 | 210000 | ||
| 3Cr13 | 400-480 | 500~600 | 18 | 480 | 210000 | ||
| 4Cr13 | 400-480 | 500-500 | 15 | 500 | 210000 | ||
| 1Cr18Ni9 2Cr18Ni9 | Wärmebehandelt | 460~520 | 580-610 | 35 | 200 | 200000 | |
| Kaltgehärtet | 800-880 | 100-1100 | 38 | 220 | 200000 | ||
| 1Cr18Ni9Ti | Wärmebehandelt erweicht | 430~550 | 54-700 | 40 | 240 | 200000 | |
Am besten ist es, eine allgemein verwendete Materialdatenbank zu erstellen und fehlende physikalische Parameter von den Lieferanten zu beziehen. Wenn die Parameter für Elastizitätsmodul und Streckgrenze korrekt sind, sind die Biegung und der Rückprall von allgemeinen Federanschlüssen, optischen Teilen und Profilen präziser.