Haben Sie sich jemals gefragt, wie man die für die Blechbearbeitung erforderliche Biegekraft genau berechnet? In diesem aufschlussreichen Blogbeitrag gehen wir auf die Feinheiten der Biegekraftberechnung ein und greifen dabei auf das Fachwissen erfahrener Maschinenbauingenieure zurück. Entdecken Sie die Schlüsselfaktoren, die die Biegekraft beeinflussen, und erfahren Sie, wie Sie bewährte Formeln zur Optimierung Ihrer Metallumformungsprozesse anwenden können. Machen Sie sich bereit, Ihr Wissen über das Biegen von Blechen auf ein neues Niveau zu heben!


Die derzeit weit verbreiteten Formeln zur Berechnung der Biegekraft wurden aus ausländischen Quellen übernommen, ohne dass Informationen über ihre Herkunft oder ihren Anwendungsbereich vorliegen.
Dieser Artikel enthält eine systematische Analyse der Herleitung der Formel zur Berechnung der Biegekraft sowie der erforderlichen Parameter.
Außerdem wird ein neuer Ansatz zur Berechnung der Biegekraft eingeführt, um den Anwendungsbereich zu erweitern.
Die Berechnung der Biegekraft für Bleche ist für genaue und effiziente Biegeprozesse unerlässlich. Das Verständnis dieser Berechnungen hilft bei der Auswahl geeigneter Werkzeuge und gewährleistet qualitativ hochwertige Biegungen. Dieses Kapitel gibt einen Überblick über die wichtigsten Konzepte, Werkzeuge und praktischen Tipps zur Berechnung der Biegekraft bei der Blechbearbeitung.
Biegekraftberechnungen sind bei der Blechbearbeitung von entscheidender Bedeutung, um sicherzustellen, dass während des Biegevorgangs die richtige Kraft aufgebracht wird. Dadurch werden Materialverschwendung und Werkzeugschäden vermieden und die gewünschte Biegequalität sichergestellt. Genaue Berechnungen helfen bei der Auswahl der richtigen Abkantpresse und des richtigen Werkzeugs, was zu einer effizienten Produktion und Kosteneinsparungen führt.
Die Biegekraft ( F ), die erforderlich ist, um ein Blech zu biegen, kann mit der folgenden Formel berechnet werden:
wo:
Der Innenradius ( R ) der Biegung wird häufig auf der Grundlage der Matrizenöffnung ( V ) geschätzt:
Die Matrizenöffnung ( V ) wird in Abhängigkeit von der Blechdicke ( S ) gewählt:
Die Mindestflanschlänge stellt sicher, dass das Material während des Biegevorgangs nicht herunterfällt und wird unter Berücksichtigung der Matrizenöffnung und des Biegewinkels berechnet.
In den letzten Jahren hat die Abkantpresse hat sich in verschiedenen Branchen durchgesetzt und seine Verarbeitungsmöglichkeiten erweitert.
Trotz ihrer Beliebtheit wurde die Berechnung der Biegekraft bisher nicht systematisch diskutiert.
Derzeit gibt es ungefähr zwei Arten von Formeln zur Berechnung der Biegekraft, die in den Produkthandbüchern der verschiedenen Abkantpressenhersteller.
In der Formel:
Die vom Hersteller empfohlene Formel zur Berechnung der Biegekraft basiert auf einer bereits erwähnten Formel.
Beide Formeln wurden aus verschiedenen Produktbroschüren entnommen, es gibt jedoch keinen Nachweis für ihre Richtigkeit.
Verwandter Rechner: Tonnage-Rechner für Abkantpressen
Abbildung 1 ist eine schematische Darstellung der Biegeverfahren eines Blattes.
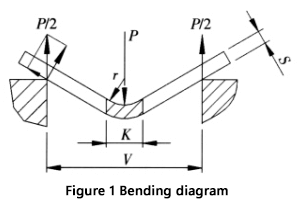
Die Berechnung der Biegekraft und ihre Parameter werden im Folgenden erläutert:
Die empfohlene Breite der unteren Matrizenöffnung (V) für das freie Biegen beträgt das 8- bis 10-fache der Blechdicke (S), mit einem Verhältnis von Breite zu Dicke von V/S = 9.
Die Hersteller von Abkantpressen geben die Werte für die Matrizenbreite (V) und den Innenradius (r) des gebogenen Werkstücks in ihrer Tabelle der Biegekraftparameter an. Das Verhältnis von Radius zu Breite ist in der Regel r = (0,16 bis 0,17) V, und in diesem Fall wird der Wert 0,16 verwendet.
Während des Biegevorgangs erfährt das Material in der Verformungszone eine erhebliche plastische Verformung, wodurch es sich um die Mittellinie biegt.
In einigen Fällen können kleine Risse an der Außenfläche des gekrümmten Bereichs auftreten.
Die Spannung in der Verformungszone, außer in der Nähe der mittleren Schicht, liegt nahe an der Zugfestigkeit des Materials, wobei der obere Teil der neutralen Schicht zusammengedrückt wird und der untere Teil unter Spannung steht.
Abbildung 2 zeigt den Querschnitt und das entsprechende Spannungsdiagramm in der Verformungszone.
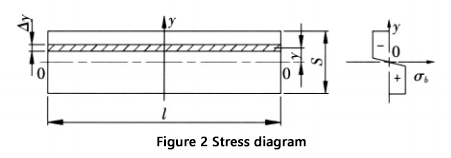
Das Biegemoment am Schnittpunkt der Verformungszone beträgt:
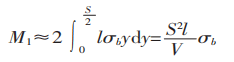
Das durch die Biegekraft in der Verformungszone erzeugte Biegemoment ist in Abbildung 1 dargestellt.
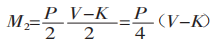
Von M1 = M2erhalten wir:

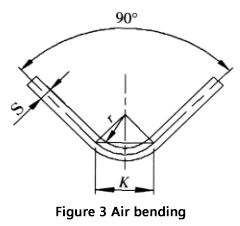
Beim Biegen eines Blechs mit einer Universalform auf einer Biegemaschine, wie in Abbildung 3 dargestellt, werden die meisten Bleche auf 90° gebogen. In diesem Fall ist K:
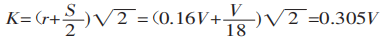
Setzt man K in Gleichung (1) ein, erhält man:
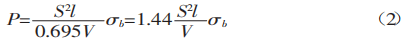
Die Zugfestigkeit gewöhnlicher Materialien, σb, beträgt 450 N/mm². Dieser Wert kann in Formel (2) verwendet werden, um das Ergebnis zu berechnen.
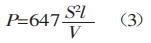
Die hier ermittelte Formel zur Berechnung der Biegekraft stimmt mit den Angaben in ausländischen Broschüren überein.
Die Variablen in der Formel sind:
Wie aus dem Herleitungsprozess ersichtlich, müssen bei der Verwendung der Formeln (2) oder (3) zur Berechnung der Biegekraft zwei zusätzliche Bedingungen erfüllt sein: Das Verhältnis von Breite zu Dicke (V/S) muss gleich 9 sein, und das Verhältnis von Radius zu Breite muss gleich 0,16 sein.
Wenn diese Bedingungen nicht erfüllt sind, kann es zu erheblichen Fehlern kommen.
Die Berechnung der Biegekraft kann kompliziert sein, wenn die beiden zusätzlichen Anforderungen (Verhältnis Breite/Dicke V/S = 9 und Verhältnis Radius/Breite = 0,16) aufgrund von Konstruktions- oder Verfahrenseinschränkungen nicht erfüllt werden können.
In solchen Situationen ist es ratsam, die folgenden Schritte zu befolgen:
Diese Schritte liefern ein präziseres und zuverlässigeres Ergebnis als die Verwendung der üblichen Formel. Ein Beispiel zur Veranschaulichung dieses Prozesses ist in Abbildung 4 dargestellt.
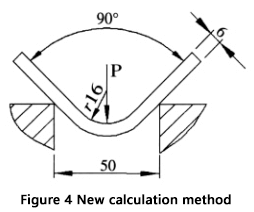
Gegeben: Blechdicke (S) = 6mm, Blechlänge (l) = 4m, Biegeradius (r) = 16mm, Öffnungsweite der unteren Matrize (V) = 50mm, und Materialzugfestigkeit (σb) = 450N/mm².
Frage: Wie kann man die erforderliche Biegekraft für das Luftbiegen berechnen?
Hier sind die Schritte:
Berechnen Sie zunächst das Verhältnis von Breite zu Dicke und das Verhältnis von Radius zu Breite:
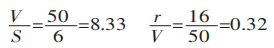
Berechnen Sie dann die projizierte Breite des Deformationsbereichs:
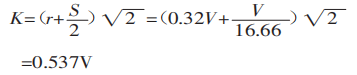
Schließlich wird mit Formel (1) die Biegekraft berechnet:
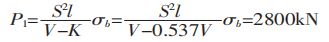
Wird die üblicherweise empfohlene Formel zur Berechnung der Biegekraft verwendet:
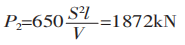
Aus P1/P2 = 1,5 lässt sich ableiten, dass die Differenz zwischen P1 und P2 das 1,5-fache beträgt.
Der Grund für diese Diskrepanz ist, dass in diesem Beispiel der Biegeradius relativ groß ist, was zu einer größeren verformten Fläche führt und daher eine größere Biegekraft erfordert.
Das Verhältnis von Radius zu Breite beträgt in diesem Beispiel 0,32 und übertrifft damit die zuvor genannten Kriterien.
Die Verwendung der Standardformel zur Berechnung der Biegekraft ist für dieses Szenario nicht geeignet. Die Vorteile der neuen Berechnungsmethode sind in diesem Beispiel zu sehen.
Außerdem steht ein Online-Rechner zur Verfügung, mit dem die Biegekraft nach der neuen Methode berechnet werden kann.
Tabelle der Zugfestigkeit
| Material | Zugfestigkeit | ||
|---|---|---|---|
| Amerikanisch | Europäisch | China | N/mm² |
| 6061 Aluminium | Alu50 | LD30 | 290 |
| 5052 Aluminium | Alu35 | LF2 | 303 |
| 1010 Baustahl | DC01 | 10/10F | 366 |
| A 536 -80 G 60-40-18 | GGG-40 | QT400-18 | 400 |
| A 351 G CF 8 | G-X 6CrNi 18 9 | Q235 | 450 |
| A 572 G50 | S 355 MC | Q345 | 550 |
| 304 Edelstahl | Inox V2A | 0Cr18Ni9 | 586 |
| 316 Edelstahl | Inox V4A | 0Cr17Ni12Mo2 | 600 |
| 4140 Niedrig legiert | 42 CrMo 4 | 42CrMo | 1000 |
Die Formeln zur Berechnung der Prägeparameter unterscheiden sich vom Luftbiegen.

1. Breite der Matrizenrinne:
V = Feinblech Dicke × 5
2. Der Innenradius wird durch die Stempelspitze bestimmt, die nach der folgenden Formel gewählt werden sollte:
Radius = Blechdicke × 0.43.
3. Für das Prägen erforderliche Kraft:
F(kn/m)=Dicke2×1,65×Zugfestigkeit (N/mm)2)×4,5/Gewindebreite
4. Die Formel für die Berechnung der minimalen Innenkante bleibt gleich:
Minimale innere Kante = Die vee × 0.67

Einige Werkzeuge benötigen eine bestimmte Kraft, um das Blech nachzugeben und die Rückfederung zu beherrschen, um das gewünschte Profil zu erhalten.
Als Beispiel betrachten wir die Kniehebelwerkzeuge, die zwei Biegungen auf einmal mit einem kurzen Abstand zwischen Biegung und Gegenbiegung ausführen.
Da diese Werkzeuge zwei Biegungen auf einmal machen, Rückfederung muss durch Prägung vollständig aufgehoben werden.
Die Gleichung zur Berechnung der erforderlichen Kraft lautet:

Knebelwerkzeuge bestehen in der Regel aus einem Einsatzhalter, in dem die auf den Knebel und den gewünschten Winkel abgestimmten Knebelwerkzeuge mit Madenschrauben befestigt werden.
Es ist wichtig, vor dem Kauf eine technische Beratung durch den Hersteller einzuholen, da diese Systeme nur dünne Bleche biegen können, maximal 2 mm, aber die maximale Dicke hängt von der Art des Einsatzes ab und kann weniger als 2 mm betragen.
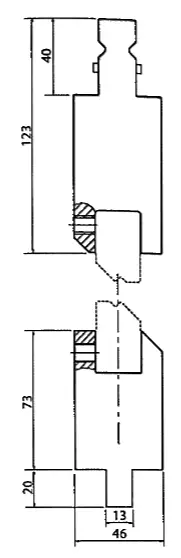
Nachstehend finden Sie Antworten auf einige häufig gestellte Fragen:
Die Zugfestigkeit spielt eine entscheidende Rolle bei der Bestimmung der erforderlichen Biegekraft für Bleche. Die Zugfestigkeit ist die maximale Spannung, die ein Material beim Dehnen aushalten kann, bevor es bricht. Wenn ein Blech gebogen wird, wird es sowohl auf Zug als auch auf Druck beansprucht. Die Außenfläche der Biegung wird auf Zug beansprucht, während die Innenfläche auf Druck beansprucht wird.
Die erforderliche Biegekraft wird direkt von der Zugfestigkeit des Materials beeinflusst, da eine höhere Zugfestigkeit bedeutet, dass das Material einer größeren Belastung standhalten kann, ohne zu versagen. Dies bedeutet, dass bei Materialien mit höherer Zugfestigkeit eine größere Kraft erforderlich ist, um das gleiche Maß an Biegung zu erreichen, als bei Materialien mit geringerer Zugfestigkeit.
Zur Berechnung der Biegekraft wird die Biegespannung, die mit der Zugfestigkeit zusammenhängt, herangezogen. Die Formel für die Biegespannung lautet
umfasst das Biegemoment (M), den Abstand von der neutralen Achse zur äußersten Faser (c) und das Trägheitsmoment des Querschnitts (I). Das Biegemoment wird von der aufgebrachten Kraft und der Länge des Hebelarms beeinflusst. Um ein Versagen beim Biegen zu verhindern, muss sichergestellt werden, dass die Biegespannung die Zugfestigkeit des Materials nicht übersteigt.
Zusammenfassend lässt sich sagen, dass eine höhere Zugfestigkeit eine höhere Biegekraft erfordert, um ein Blech zu biegen, ohne dass es versagt, was deutlich macht, wie wichtig die Berücksichtigung der Materialeigenschaften bei der Berechnung der Biegekraft ist.
Bei der Berechnung der Biegekraft für Bleche müssen mehrere Schlüsselfaktoren berücksichtigt werden, um genaue und zuverlässige Ergebnisse zu gewährleisten. Zu den wichtigsten Faktoren, die die Biegekraftberechnung beeinflussen, gehören:
Die Materialeigenschaften spielen eine entscheidende Rolle, insbesondere die Zugfestigkeit und die Streckgrenze. Die Zugfestigkeit ist die maximale Spannung, die ein Material aushalten kann, bevor es versagt, wobei die verschiedenen Materialien unterschiedliche Stärken aufweisen. Aluminium hat beispielsweise eine Zugfestigkeit von 200-300 N/mm², Baustahl (Q235) liegt bei 370-500 N/mm² und Edelstahl bei etwa 650-700 N/mm². Die Streckgrenze bestimmt die Spannung, bei der das Material beginnt, sich plastisch zu verformen, wobei eine höhere Streckgrenze mehr Biegekraft erfordert.
Die Materialdicke wirkt sich erheblich auf die Biegekraft aus, da dickere Materialien einer Verformung mehr Widerstand entgegensetzen, was eine höhere Kraft erfordert. Die Berechnungsformeln enthalten in der Regel die Materialdicke als Schlüsselvariable.
Biegeradius und -winkel sind ebenfalls wichtig. Der innere Biegeradius oder der Radius der Biegung beeinflusst die benötigte Kraft, wobei kleinere Radien aufgrund der erhöhten Spannungskonzentration mehr Kraft erfordern. Der Biegewinkel wirkt sich auf die erforderliche Kraft aus, wobei die meisten Berechnungen auf einer 90-Grad-Biegung basieren, jedoch Anpassungen für andere Winkel erforderlich sind.
Die Werkzeug- und Matrizenkonfiguration, insbesondere die untere V-Öffnung der Matrize, beeinflusst die Biegekraft. Die Breite des unteren Matrizenkanals in der Biegemaschine hängt von der Materialstärke ab, und das Präzisionsbiegen kann bei dünneren Materialien eine engere V-Öffnung erfordern.
Der K-Faktor und die Position der neutralen Achse beeinflussen ebenfalls den Biegeprozess. Der K-Faktor steht zwar in direkterem Zusammenhang mit der Berechnung von Biegezugaben und -abzügen, wirkt sich aber auf das gesamte Biegeverhalten und die erforderliche Kraft aus, indem er bestimmt, wo das Material weder gestaucht noch gedehnt wird.
Schließlich wird für die Berechnung der Biegekraft in der Regel eine Formel verwendet, die die Zugfestigkeit des Materials, die Dicke und die Länge der Biegung berücksichtigt. Eine vereinfachte Formel für kohlenstoffarmen Stahl lautet zum Beispiel:
wobei ( t ) die Dicke in mm und ( l ) die Länge in Metern ist, mit dem Ergebnis in Tonnen.
Wenn Sie diese Faktoren berücksichtigen, können Sie die für das Biegen von Blechen erforderliche Biegekraft genau berechnen und sicherstellen, dass die Abkantpresse richtig eingestellt ist, um die gewünschte Biegung ohne Materialversagen oder übermäßige Verformung zu erreichen.
Um die richtigen Einstellungen für eine Abkantpresse zu ermitteln, müssen Sie mehrere wichtige Faktoren berücksichtigen, um ein präzises und effizientes Biegen von Blechen zu gewährleisten. Ermitteln Sie zunächst die Materialart und -dicke, da diese die erforderliche Biegekraft erheblich beeinflussen. Verschiedene Metalle wie Edelstahl und Aluminium haben unterschiedliche Festigkeiten und Elastizitäten, die sich auf die zum Biegen erforderliche Kraft auswirken.
Berechnen Sie anschließend die erforderliche Tonnage anhand der Formel ( P=650S²L/V ), wobei ( P ) die Biegekraft, ( S ) die Dicke des Blechs und ( V ) die Öffnung des Unterwerkzeugs ist. Berücksichtigen Sie die Biegelänge und den Biegewinkel, da schärfere Winkel eine höhere Tonnage erfordern. Stellen Sie sicher, dass das Material richtig gestützt und ausgerichtet wird, um Durchbiegung und Ungenauigkeiten zu vermeiden.
Verschiedene Biegeverfahren wie Luftbiegen, Bodenbiegen und Prägen erfordern unterschiedliche Tonnagen, wobei das Luftbiegen die Basis ist und das Prägen etwa die achtfache Tonnage des Luftbiegens erfordert. Stellen Sie sicher, dass die Tonnage die zentrale Tonnagegrenze der Abkantpresse nicht überschreitet, um eine Überlastung und mögliche Schäden zu vermeiden.
Wählen Sie geeignete Werkzeuge aus, die dem Material und den Biegeanforderungen entsprechen, und stellen Sie sicher, dass die Werkzeuge richtig ausgerichtet und installiert sind. Kalibrieren Sie die Maschine, indem Sie sie inspizieren und reinigen, den Hinteranschlag einstellen und die Position und den Winkel des Stößels kalibrieren. Programmieren Sie die Abkantpresse entsprechend der berechneten Tonnage und den Biegeparametern und führen Sie einen Probelauf mit Ausschussmaterial durch, um die Einstellungen fein abzustimmen und die gewünschten Ergebnisse zu erzielen.
Wenn Sie diese Schritte befolgen, können Sie die geeigneten Einstellungen für Ihre Abkantpresse genau bestimmen, was zu präzisen und effizienten Blechbiegevorgängen führt.
Die Formeln und Schritte zur Berechnung der Biegekraft eignen sich nicht nur für das winklige Biegen eines Blechs, sondern auch für das bogenförmige Biegen (das technisch als Winkelbiegen mit großem Biegeradius bezeichnet werden sollte).
Es ist von entscheidender Bedeutung, dass das Formen einer Bogenform ein einzigartiges Formdesign erfordert.
Bei der Projektion des Verformungsbereichs muss die Berechnung auf den während des Prozesses ermittelten Prozessparametern basieren, die nicht durch eine einzige Formel bestimmt werden können.
In einer bestimmten Eisenturmfabrik haben wir erfolgreich einen Zylinder mit einer Wandstärke von 12 mm, einem Durchmesser von 800 mm und einer Länge von 16 m mit einer 28000-kN-Presse gebogen. Bremsmaschine und eine runde Form.
Die in diesem Artikel beschriebene Methode wurde zur Bestimmung der Biegekraft angewandt und führte zu zufriedenstellenden Ergebnissen bei der Konstruktion einer Form für eine Bogenform.
Lesen Sie weiter: