Wie kann ein einfaches Kurven- und Mitnehmersystem zu einer effizienten, präzisen Bewegung in komplexen Maschinen führen? Dieser Artikel befasst sich mit den Feinheiten der Konstruktion von Kurvenscheibenantrieben und erklärt die verschiedenen Arten von Kurvenscheiben und Mitnehmern, ihre Bewegungswege und wie man eine optimale Leistung erzielt. Von den grundlegenden Komponenten bis hin zu fortschrittlichen Konstruktionsmethoden erhalten die Leser wertvolle Einblicke in die Entwicklung hocheffizienter Kurvensysteme. Freuen Sie sich auf praktische Tipps und detaillierte Analysen, die Ihr Verständnis und Ihre Anwendung von Kurvenmechanismen in technischen Projekten verbessern werden.
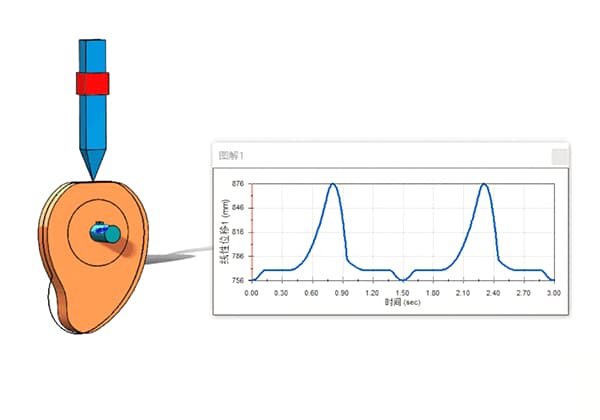
Der Nockenmechanismus besteht in der Regel aus zwei beweglichen Teilen, nämlich dem Nocken und dem Mitnehmer, die beide am Rahmen befestigt sind. Die Nockenvorrichtung ist sehr vielseitig und kann fast jede beliebige Bewegung erzeugen.
Eine Nocke kann als ein Bauteil mit einer gekrümmten Oberfläche oder Rille definiert werden. Durch Schwenken oder Drehen dieses Bauteils kann ein anderes Bauteil, der Mitnehmer, eine vorgegebene Bewegung ausführen. Der Weg des Mitnehmers ist meist auf einen Schlitz begrenzt, um eine Hin- und Herbewegung zu erreichen.
Manche Mechanismen stützen sich beim Rücklauf auf ihr eigenes Gewicht, andere verwenden Federn als Rückstellkraft, um präzise Bewegungen zu erreichen. Andere verwenden Führungsschienen, um sich entlang bestimmter Bahnen zu bewegen.
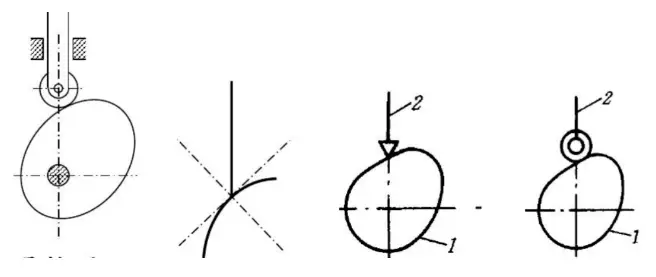
Je nach der Form der Nocken kann man sie in drei Typen unterteilen: Scheibennocken, bewegliche Nocken und zylindrische Nocken.
Die Anhänger lassen sich nach ihren Enden in drei Typen unterteilen: Spitzanhänger, Rollenanhänger und Flachbodenanhänger.
Aufgrund des punktuellen Kontakts zwischen der Kurvenrolle und der Nocke, der zu einer hohen Belastung und schnellem Verschleiß führt, ist sie nicht für langsam laufende Kurvengetriebe mit großen Stößen geeignet. Die Rollenrolle kann diese Nachteile ausgleichen.
Um den Wirkungsgrad der Übertragung zu verbessern, kann man auch einen Flachbodenläufer einführen, der senkrecht zur Kraftrichtung auf der Unterseite steht.
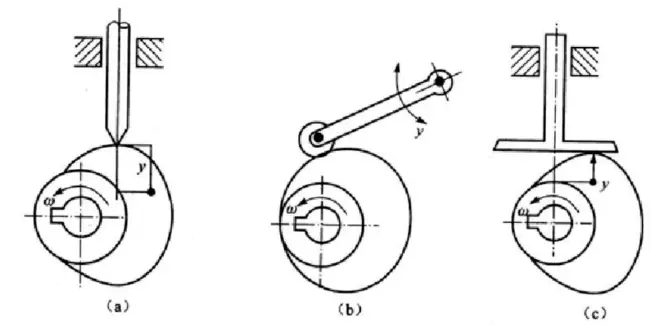
Die zuvor betrachteten Übertragungskomponenten haben die Form einer geradlinigen Bewegung, sie können aber auch die Form einer schwingenden Bewegung haben. Im ersten Fall spricht man von einem direkt wirkenden Mitnehmer, im zweiten Fall von einem schwingenden Mitnehmer.
Wir können auch dafür sorgen, dass das Zentrum der Nockendrehung nicht auf dem linearen Pfad der Bewegung des Mitnehmers liegt. In diesem Fall sprechen wir von einem Versatz. Liegt der Drehpunkt auf dem linearen Weg der Mitnehmerbewegung, spricht man von konzentrisch.
Darüber hinaus können wir auch Methoden zur Aufrechterhaltung von hochbelasteten Verriegelungsbeziehungen in Betracht ziehen und den Mechanismus in geometrische Verriegelung und Kraftverriegelung unterteilen.
Durch die Kombination der Nockenform, des Endes des Mitnehmers und der Bewegungsmuster des Mitnehmers kann der Name des entworfenen Mechanismus bestimmt werden, wie z. B.: die Kurvenscheibe mit einem direkt wirkenden Mitnehmer mit scharfer Nase (relative Position des Mitnehmers - Nocken + Ende des Mitnehmers + Bewegungsmuster des Mitnehmers + Nockenform).
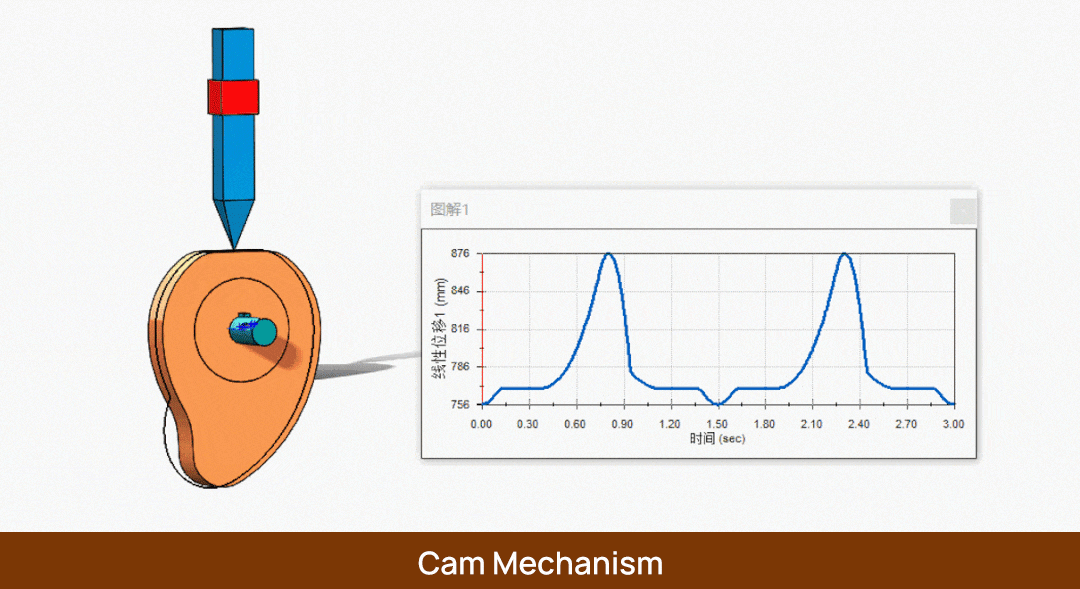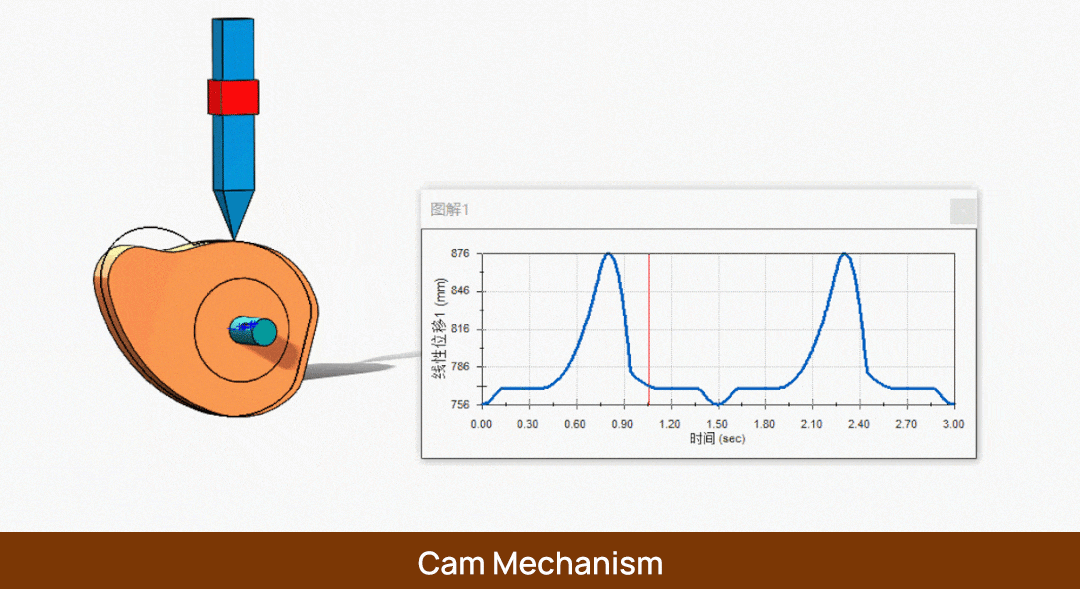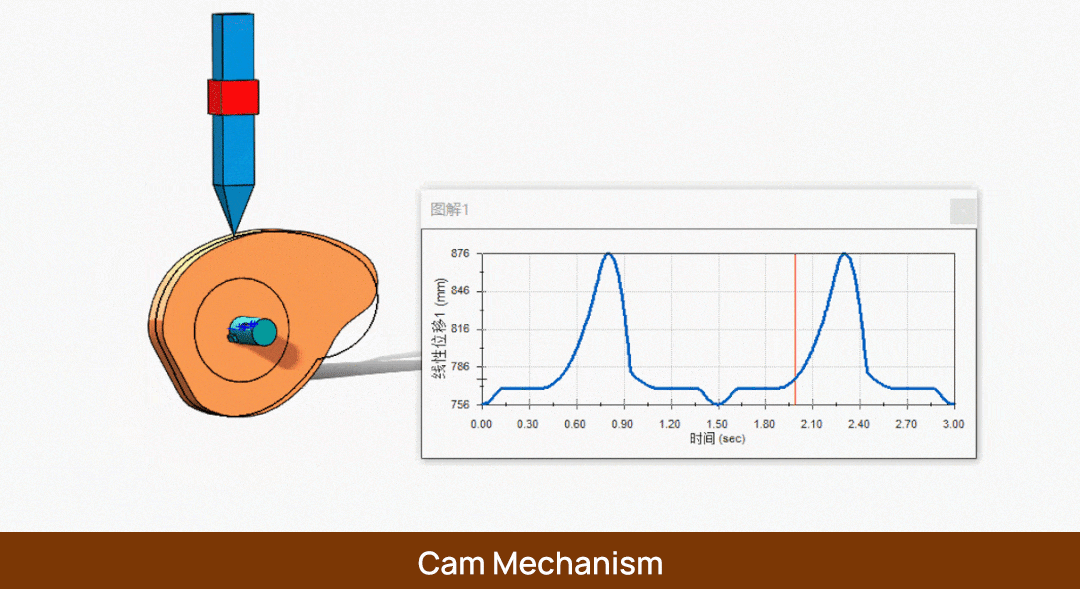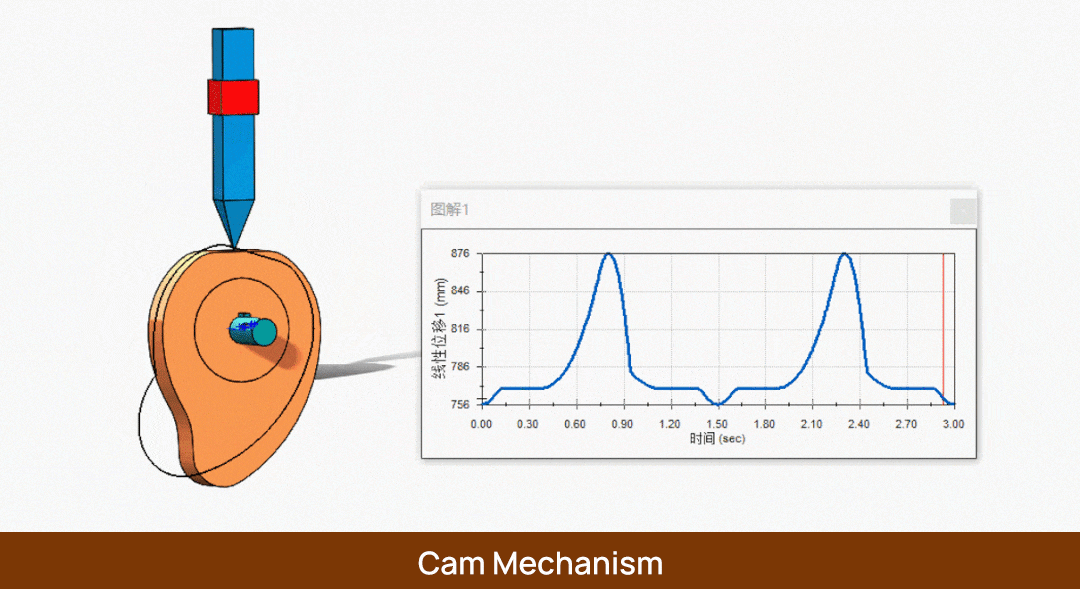
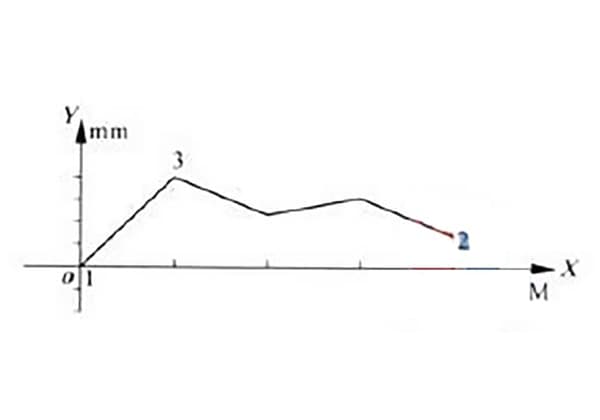
Zunächst haben wir eine Nocke, auf der ein Mitnehmer sitzt. Wenn sich die Nocke mit einer Winkelgeschwindigkeit ω um φs Grad dreht, bewegt sich der Mitnehmer nicht. Zu diesem Zeitpunkt bezeichnen wir φs als Verweilwinkel, und der entsprechende Kreis wird als Grundkreis bezeichnet. Ebenso wird der Radius dieses Kreises als Grundkreisradius r0 bezeichnet.
Wenn wir dann die Nocke mit einer Winkelgeschwindigkeit ω um φ Grad weiterdrehen, steigt der Mitnehmer um h. Zu diesem Zeitpunkt bezeichnen wir φ als Hubwinkel und h als Hub.
Später, wenn der Mitnehmer den Punkt h erreicht, lassen wir ihn für eine gewisse Zeit stehen. In der Zwischenzeit dreht sich der Nocken um φs', was dem Hubwinkel entspricht.
Schließlich müssen wir den Mitnehmer wieder in seine ursprüngliche Position bringen, also drehen wir die Nocke um φ'. Zu diesem Zeitpunkt kehrt der Mitnehmer zum Ausgangspunkt zurück. Wir nennen φ' den Rückkehrwinkel.
Es gibt zwei Hauptmethoden für den Entwurf von Kurvenmechanismen, zum einen die grafische Methode und zum anderen die analytische Methode.
Ersteres ist relativ einfach, da nur das gewünschte Diagramm der Schubbewegung bereitgestellt werden muss und dann die entsprechende Konturkurve auf der Grundlage der durch das Diagramm bereitgestellten Winkel-Prozess-Beziehung ermittelt werden kann.
Die Genauigkeit ist nicht sehr hoch. Letztere wird berechnet, und ihre Berechnung ist relativ komplex, was für die Konstruktion von Kurvenmechanismen mit hohen Genauigkeitsanforderungen geeignet ist.
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
AR 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO