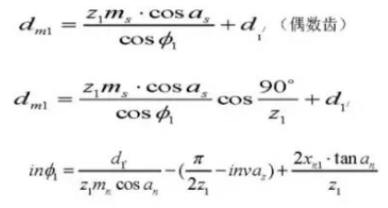Haben Sie sich jemals über die faszinierende Welt der Zahnräder gewundert? In diesem Blogbeitrag werden wir uns mit der Geschichte, den Arten und der Terminologie dieser wichtigen mechanischen Komponenten befassen. Lassen Sie sich von einem erfahrenen Maschinenbauingenieur in die Geheimnisse der Zahnräder einweihen. Entdecken Sie, wie sich Zahnräder im Laufe der Jahrhunderte entwickelt haben, und erfahren Sie mehr über ihre entscheidende Rolle in modernen Maschinen.
Ein Zahnrad ist ein präzisionsgefertigtes, verzahntes mechanisches Bauteil, das so konstruiert ist, dass es mit anderen Zahnrädern oder verzahnten Bauteilen ineinander greift. Es ist ein grundlegendes Element in Kraftübertragungssystemen, das Drehgeschwindigkeit und Drehmoment zwischen Wellen überträgt. Zahnräder zeichnen sich durch ihre kreisförmige Form mit gleichmäßig verteilten Zähnen entlang des Umfangs aus, die in der Regel einem Evolventenprofil folgen, um einen optimalen Eingriff zu ermöglichen.
Die Anwendung von Zahnrädern in der mechanischen Übertragung und im gesamten Bereich des Maschinenbaus ist außerordentlich vielfältig und entscheidend. Sie sind Bestandteil einer Vielzahl von Maschinen und Geräten, von einfachen handbetriebenen Werkzeugen bis hin zu komplexen Industrieanlagen und Hochleistungsfahrzeugen. Zahnräder ermöglichen eine präzise Steuerung von Geschwindigkeit, Richtung und Kraft in mechanischen Systemen und sind daher in Antriebssträngen, Untersetzungsgetrieben, Differentialen und unzähligen anderen mechanischen Baugruppen unverzichtbar.
Die Vielseitigkeit von Zahnrädern ergibt sich aus ihrer Fähigkeit, in verschiedenen Größen, Materialien und Konfigurationen hergestellt zu werden, darunter Stirnrad-, Schräg-, Kegelrad- und Schneckenräder, die jeweils für bestimmte Anwendungen und Leistungsanforderungen geeignet sind. Im Zuge des technologischen Fortschritts werden Konstruktion und Herstellung von Zahnrädern ständig weiterentwickelt, wobei neue Werkstoffe, Produktionstechniken und Optimierungsmethoden zum Einsatz kommen, um Effizienz, Haltbarkeit und Geräuschreduzierung in mechanischen Systemen zu verbessern.
Bereits 350 v. Chr. schrieb der berühmte griechische Philosoph Aristoteles in seiner Literatur über Zahnräder.
Um 250 v. Chr. beschrieb der Mathematiker Archimedes in seiner Literatur auch die Verwendung von Turbine und Schneckengetriebe in einer Winde.
In der Wasseruhr von Ktesibios im Irak sind noch Zahnräder aus den Jahrhunderten vor Christus erhalten.
Die Geschichte der Zahnräder in China reicht bis ins Altertum zurück und hat eine lange und umfangreiche Geschichte. Historischen Aufzeichnungen zufolge waren Zahnräder im alten China bereits 400-200 v. Chr. in Gebrauch.
Die in der Provinz Shanxi ausgegrabenen Bronzezahnräder sind die ältesten bisher entdeckten Zahnräder der Welt. Geführte Wagen, die die Errungenschaften der antiken Wissenschaft und Technik widerspiegeln, waren mechanische Geräte, die sich um Zahnradmechanismen drehten.
Während der italienischen Renaissance in der zweiten Hälfte des 15. Jahrhunderts hat das berühmte Universalgenie Leonardo da Vinci nicht nur kulturelle und künstlerische Aspekte unauslöschlich geprägt, sondern auch bedeutende Beiträge zur Geschichte der Zahnradtechnik geleistet.
Nach mehr als 500 Jahren sind in den heutigen Zahnrädern noch die Prototypenskizzen von damals zu sehen.
(1) Stirnrad
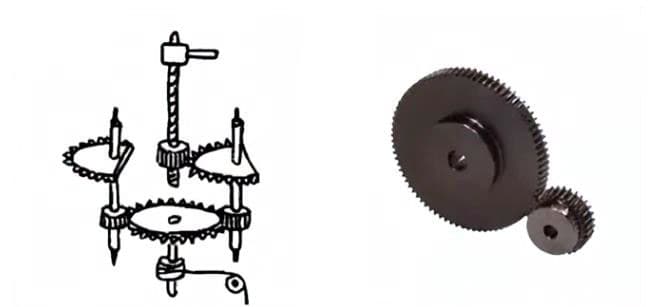
(2) Zahnstange und Ritzel
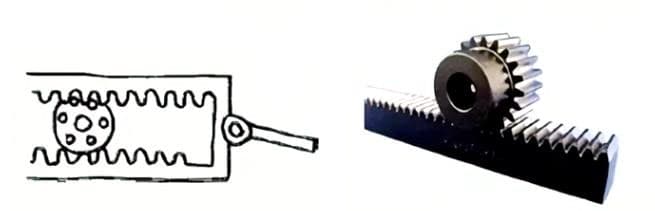
(3) Stirnradgetriebe mit gekreuzten Achsen
(4) Kegelrad
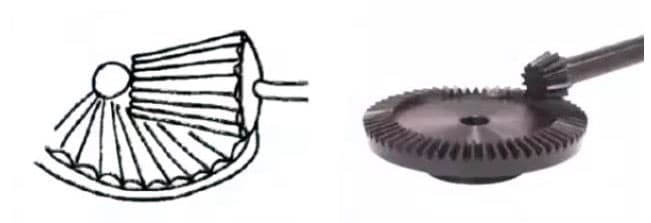
(5) Hypoid-Kegelradgetriebe mit hohem Übersetzungsverhältnis
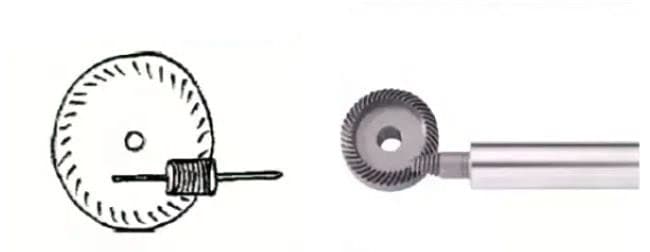
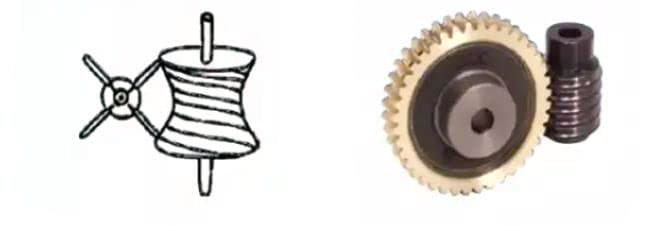
(6) Schneckengetriebe
Erst im späten 17. Jahrhundert begann man, sich mit der Zahnform des Rades zu befassen, die eine präzise Bewegungsübertragung ermöglichte. Nach der industriellen Revolution in Europa im 18. Jahrhundert verbreitete sich die Anwendung von Zahnrädern zunehmend.
Zunächst wurde das Zykloidenrad entwickelt, dann das Evolventenrad. Zu Beginn des 20. Jahrhunderts hatte sich das Evolventenrad in seiner Anwendung durchgesetzt. Später wurden Zahnräder wie das Schrägstirnrad, das Bogenrad, das Kegelrad und das Schrägrad entwickelt.
Heute hat die moderne Getriebetechnik große Fortschritte gemacht. Die Zahnradmodule reichen von 0,004 bis 100 Millimeter, der Zahnraddurchmesser kann von 1 Millimeter bis 150 Meter reichen. Die Kraftübertragung Die Leistung kann bis zu 100.000 Kilowatt erreichen, und die Rotationsgeschwindigkeit kann bis zu 100.000 Umdrehungen pro Minute betragen. Die höchste Umfangsgeschwindigkeit kann bis zu 300 Meter pro Sekunde erreichen.
Die Entwicklung von Getrieben für die Kraftübertragung geht international in Richtung Miniaturisierung, hohe Geschwindigkeit und Standardisierung. Zu den Trends in der Getriebekonstruktion gehören der Einsatz von Spezialgetrieben, die Entwicklung von Planetengetrieben und die Erforschung und Entwicklung von vibrations- und geräuscharmen Getrieben.
Es gibt verschiedene Arten von Zahnrädern, und die gebräuchlichste Methode zur Klassifizierung basiert auf der Achse des Zahnrads.
Im Allgemeinen werden Zahnräder in drei Typen eingeteilt: mit parallelen Achsen, mit sich kreuzenden Achsen und mit schrägen Achsen.
Parallelachsige Zahnräder: einschließlich Stirnrädern, Schrägstirnrädern, Innenverzahnungen, Zahnstangen und Schrägstirnrädern.
IGetrieben mit sich überschneidender Achse: einschließlich gerader Kegelräder, Spiralkegelräder, Null-Grad-Kegelräder, usw.
Zahnräder mit schräger Achse: einschließlich schrägverzahnter Zahnräder mit gekreuzten Achsen, Schneckenräder, Hypoidkegelräder, usw.
| Art der Getriebeübertragung | Art des Fanggeräts | Wirkungsgrad der Übertragung (%) | Grafische 3D-Darstellung |
Parallel-Achse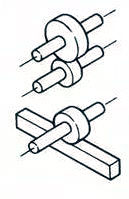 | Stirnradgetriebe | 98.0-99.5 |  |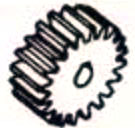
| Schrägverzahnte Getriebe |  | ||
| Zahnstangen,Spiralförmige Zahnstangen |  | ||
| Interne Gänge |  | ||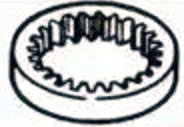
Schnittpunkt der Achsen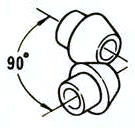 | Gehrungszahnräder | 98.0-99.0 |  |
| Geradverzahnte Kegelräder |  | ||
| Spiralförmige Kegelräder |  | ||
Schräg-Achse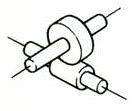 | Schneckengetriebe | 70.0-95.0 |  |
| Würmer | 30.0-90.0 |  | |
| Schneckenräder |  |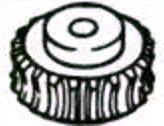
Der in der obigen Tabelle angegebene Wirkungsgrad ist der Übertragungswirkungsgrad, der die Verluste durch Lager und Rührschmierung nicht berücksichtigt. Das Ineinandergreifen von Zahnradpaaren mit parallelen und sich kreuzenden Achsen erfolgt im Wesentlichen durch Rollen, und das relative Gleiten ist sehr gering, so dass der Wirkungsgrad hoch ist.
Das Ineinandergreifen von Zahnradpaaren mit versetzten Achsen, wie z. B. Schrägstirnrädern und Schneckenrädern, hat erhebliche Auswirkungen auf die Reibung, da die Kraftübertragung durch relatives Gleiten erfolgt, was zu einer Verringerung des Übertragungswirkungsgrads im Vergleich zu anderen Zahnrädern führt.
Der Wirkungsgrad von Zahnrädern bezieht sich auf die Übertragungseffizienz von Zahnrädern in ihrem normalen Montagezustand.
Bei unsachgemäßem Einbau, insbesondere wenn der Abstand der Kegelradbaugruppe nicht korrekt ist und einen Fehler am Schnittpunkt der gleichen Kegel verursacht, sinkt der Wirkungsgrad erheblich.
1. Stirnräder
Stirnräder, bei denen die Zahn- und Achslinien parallel verlaufen. Sie sind in der Kraftübertragung weit verbreitet, weil sie leicht zu bearbeiten sind.
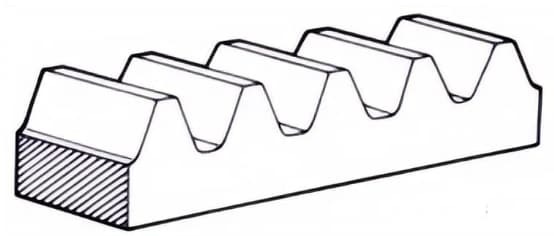
2. Gestell
Ein geradverzahntes Zahnrad, das mit Stirnrädern kämmt. Es kann als ein Sonderfall betrachtet werden, bei dem der Teilungsdurchmesser des Stirnrads unendlich groß wird.
3. Innenverzahnung
Zahnräder mit Zähnen, die auf der Innenseite eines Rings bearbeitet sind und in Stirnräder eingreifen. Sie werden hauptsächlich in Anwendungen wie Planetengetriebe und Zahnradkupplungen verwendet.
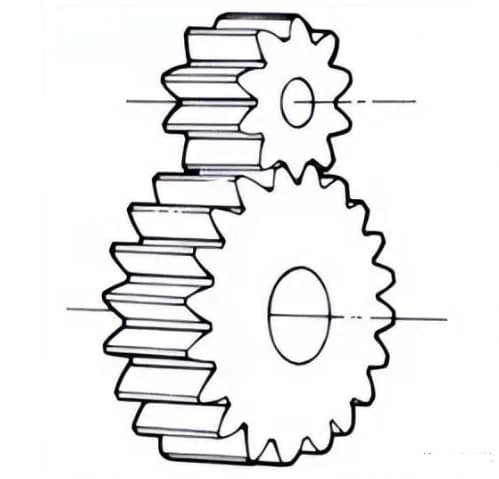
4. Schraubenförmige Zahnräder
Stirnradgetriebe mit schraubenförmig angeordneten Zähnen. Sie werden aufgrund ihrer hohen Festigkeit und ihres reibungslosen Betriebs im Vergleich zu Stirnrädern häufig verwendet. Sie erzeugen bei der Übertragung einen Axialschub.
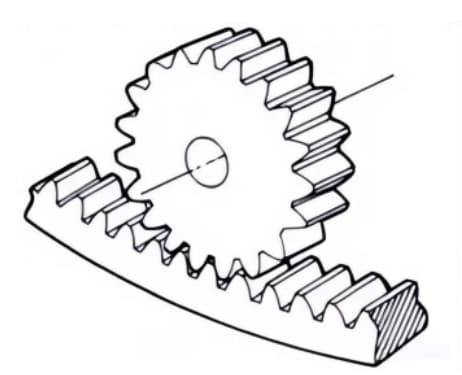
5. Spiralförmige Zahnstange
Ein Zahnstangengetriebe, das mit schrägverzahnten Rädern ineinandergreift. Es entspricht dem Fall, dass der Teilungsdurchmesser des Schrägrades unendlich groß wird.
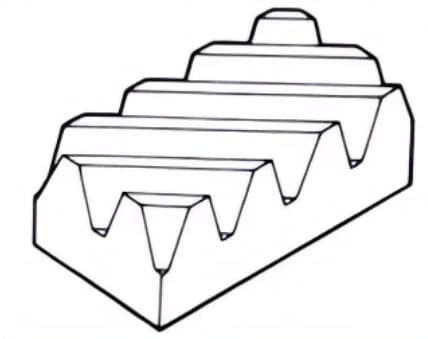
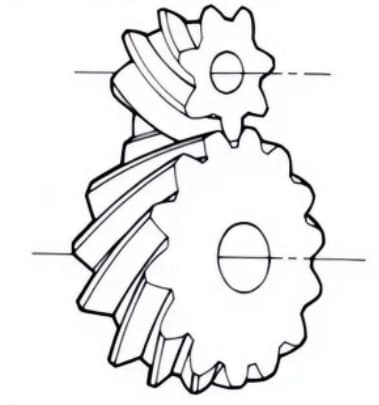
6. Fischgrätenmuster Zahnräder
Zahnräder, die aus zwei schrägverzahnten Rädern mit entgegengesetzten Schrägungswinkeln bestehen. Sie haben den Vorteil, dass sie keinen Axialschub erzeugen.
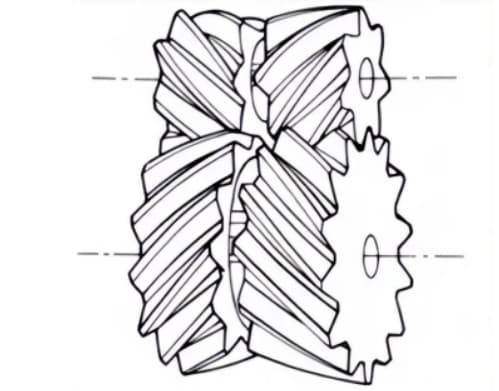
1. Geradverzahnte Kegelräder
Kegelräder mit Zahnlinien, die parallel zur Mantellinie des Kegels verlaufen. Sie sind im Vergleich zu anderen Arten von Kegelrädern relativ einfach zu fertigen.
Daher werden sie häufig in Kegelradgetrieben für die Kraftübertragung eingesetzt.
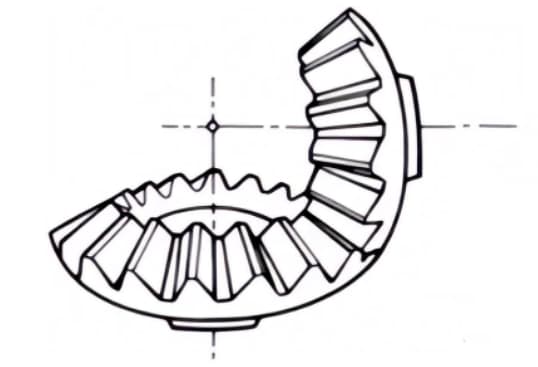
2. Spiralförmige Kegelräder
Kegelräder mit gekrümmten Zahnlinien und einem Schrägungswinkel. Obwohl sie schwieriger herzustellen sind als gerade Kegelräder, werden sie häufig als hochfeste und geräuscharme Zahnräder verwendet.
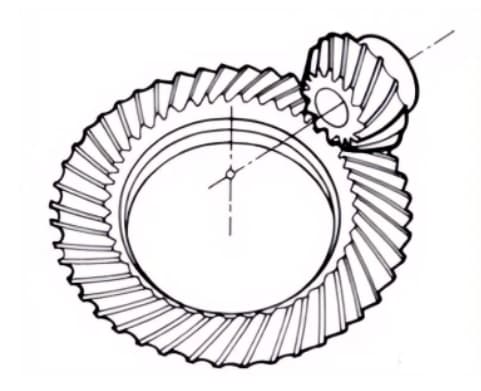
3. Null-Kegelradgetriebe
Gebogene Kegelräder mit einem Schrägungswinkel von null Grad. Sie weisen die Eigenschaften von geraden und spiralförmigen Kegelrädern auf, wobei die Zahnoberfläche der gleichen Krafteinwirkung ausgesetzt ist wie bei geraden Kegelrädern.
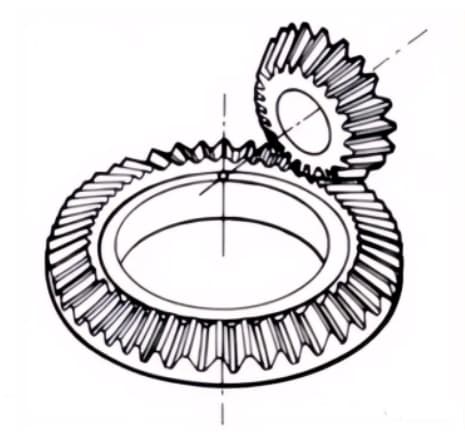
1. Schneckengetriebe-Paar
Der Begriff "Schneckenradpaar" bezieht sich auf eine Kombination aus einer Schnecke und einem mit ihr kämmenden Schneckenrad. Das größte Merkmal des Schneckenradpaares ist, dass mit nur einem Paar ein großes Übersetzungsverhältnis erreicht werden kann und sie leise arbeiten. Ihr geringer Wirkungsgrad ist jedoch ein Nachteil.
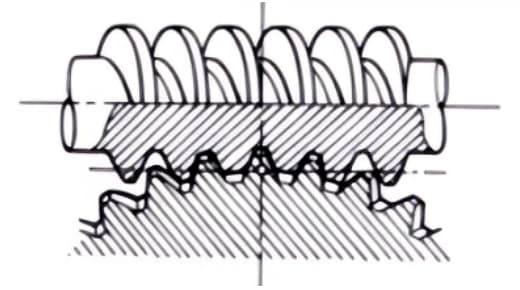
2. Stirnrad- und Schneckengetriebe-Paar
Ein Begriff, der verwendet wird, wenn zylindrische Schneckenradpaare für die Übertragung zwischen versetzten Achsen verwendet werden. Sie können bei schrägverzahnten Zahnradpaaren oder zwischen schrägverzahnten und geradverzahnten Paaren eingesetzt werden. Obwohl sie leichtgängig sind, eignen sie sich nur für den Einsatz unter leichter Belastung.
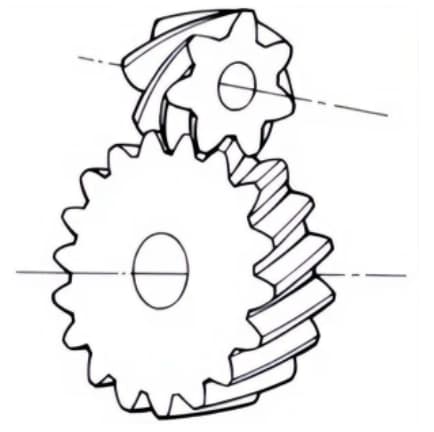
1. Stirnradgetriebe
Scheibenförmige Zahnräder, die mit Stirnrädern oder Schrägstirnrädern kämmen können. Sie werden für die Übertragung zwischen orthogonalen Achsen und versetzten Achsen verwendet.
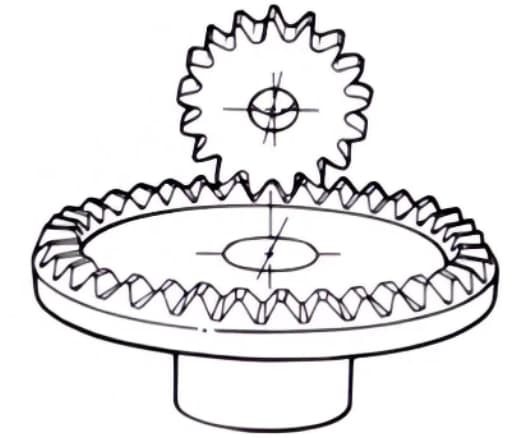
2. Sanduhr-Schneckengetriebe-Paar
Der Begriff "Sanduhr-Schneckenradpaar" bezieht sich auf eine Kombination aus einer Sanduhrschnecke und einem Schneckenrad, das mit ihr kämmt. Obwohl sie im Vergleich zu zylindrischen Schneckenrädern schwieriger herzustellen sind, können sie schwere Lasten übertragen.
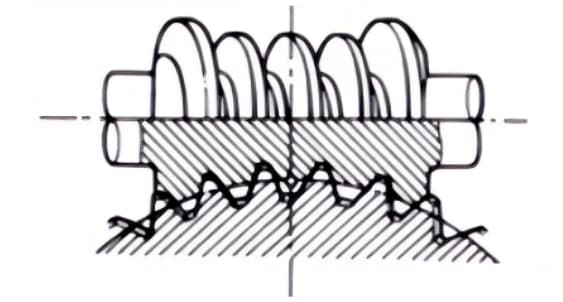
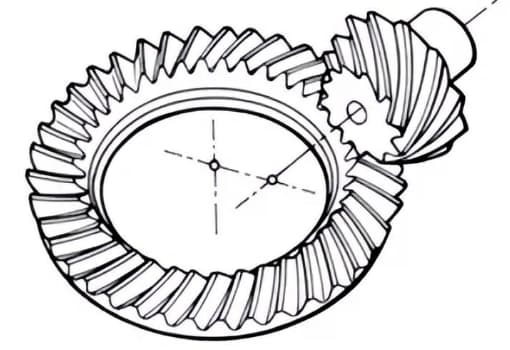
3. Hypoidzahnräder
Konische Zahnräder, die für die Übertragung zwischen versetzten Achsen verwendet werden. Die größeren und kleineren Zahnräder werden exzentrisch bearbeitet, ähnlich wie bei spiralförmigen Kegelrädern. Das Verzahnungsprinzip ist sehr komplex.
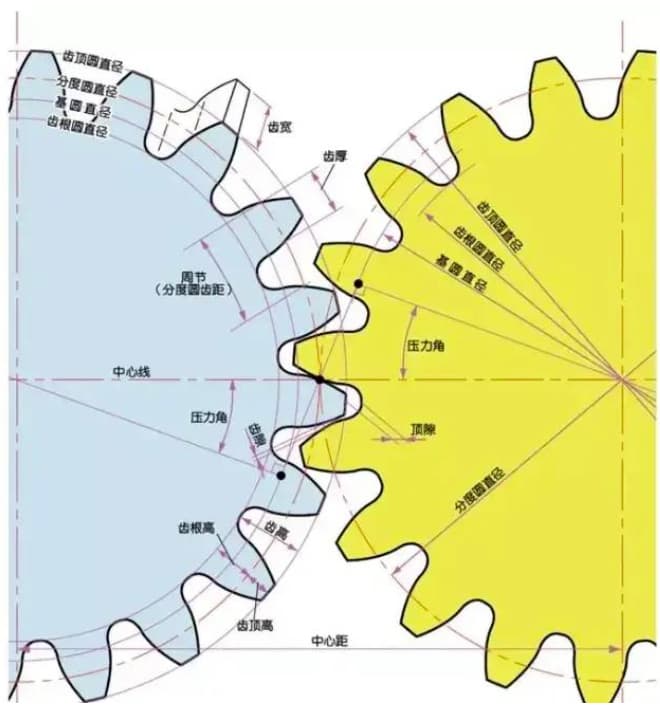
Zahnräder haben eine eigene Terminologie und Darstellungsweise. Um das Verständnis von Zahnrädern zu verbessern, werden im Folgenden einige häufig verwendete grundlegende Begriffe aus dem Bereich der Zahnräder erläutert.
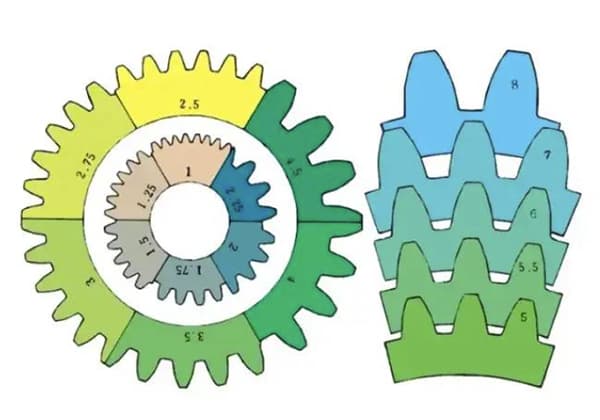
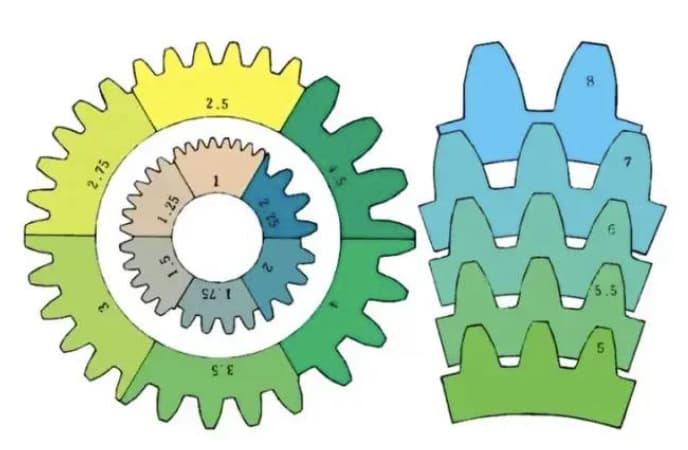
m1, m3, m8... sind als Modul 1, Modul 3 bzw. Modul 8 bekannt. Das Modul wird weltweit allgemein verwendet, um die Größe des Zahnrads anzugeben, wobei das Symbol m (Modul) und Zahlen (Millimeter) für die Größe der Zähne verwendet werden.
Je größer die Zahl, desto größer der Gang.
In Ländern, die imperiale Einheiten verwenden, wie z. B. die Vereinigten Staaten, wird die Größe der Zähne durch das Symbol DP (diametral pitch) und Zahlen (die Anzahl der Zähne für ein Zahnrad mit 1 Zoll Teilungsdurchmesser) angegeben.
Zum Beispiel: DP24, DP8 usw. Es gibt auch einen Vergleich und eine spezielle Methode zur Angabe der Größe der Zähne mit dem Symbol CP (Kreisteilung) und Zahlen (Millimeter), z. B. CP5, CP10.
Die Teilung (p) erhält man durch Multiplikation des Moduls mit pi. Die Teilung ist die Länge zwischen benachbarten Zähnen.
Die Formel lautet: p= pi x m
Vergleich der Zahngröße für verschiedene Module:
Der Eingriffswinkel ist ein Parameter, der die Form der Verzahnung bestimmt. Er bezieht sich auf die Neigung der Verzahnungsoberfläche und wird im Allgemeinen auf 20 Grad (α) eingestellt.
Früher waren Zahnräder mit einem Eingriffswinkel von 14,5 Grad üblich.
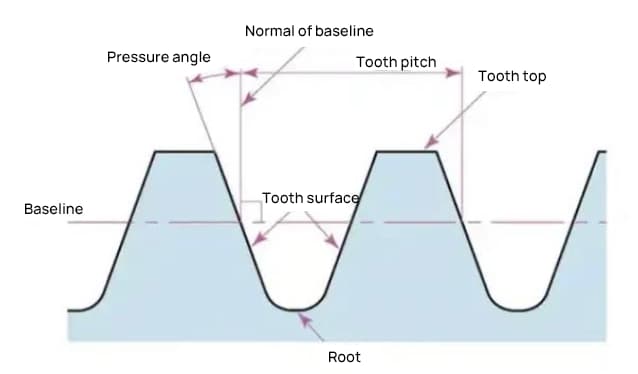
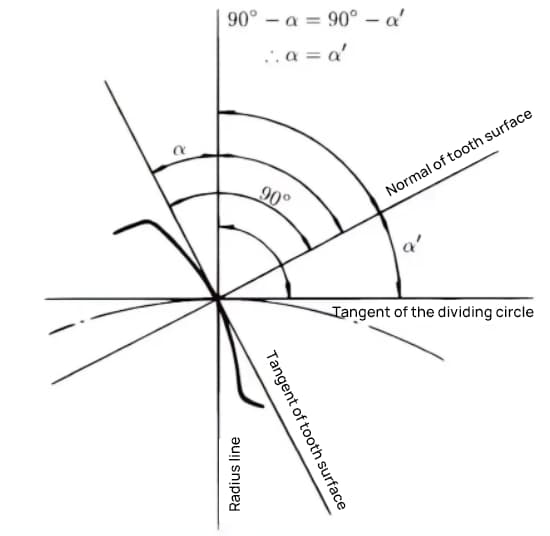
Der Eingriffswinkel ist der Winkel, der zwischen dem Radius und der Tangente an die Zahnform in einem bestimmten Punkt der Zahnoberfläche (im Allgemeinen dem Knoten) gebildet wird. Wie in der Abbildung dargestellt, ist α der Eingriffswinkel. α' ist ebenfalls ein Eingriffswinkel, da α' = α.
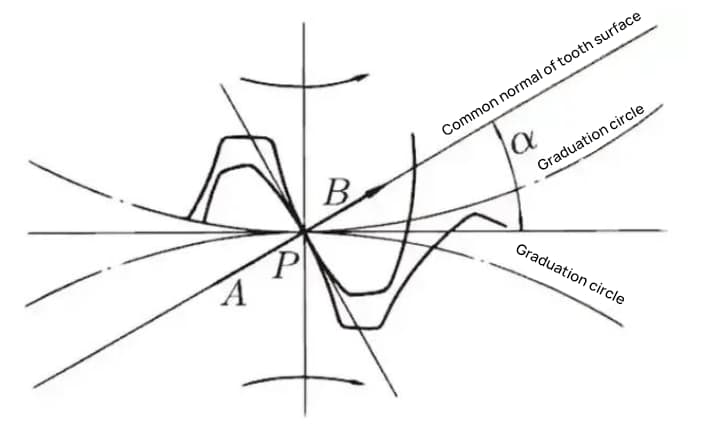
Wenn der Eingriffszustand von Rad A und Rad B vom Knotenpunkt aus betrachtet wird, schiebt Rad A das Rad B vom Knotenpunkt aus. Zu diesem Zeitpunkt wirkt die treibende Kraft auf die gemeinsame Normale von Zahnrad A und Zahnrad B. Mit anderen Worten: Die gemeinsame Normale ist die Richtung der Kraft und die Richtung des Drucklagers, wobei α der Eingriffswinkel ist.
Der Modul (m), der Eingriffswinkel (α) und die Anzahl der Zähne (z) sind die drei grundlegenden Parameter eines Zahnrads. Auf dieser Grundlage wird jeder Teil des Zahnrads in Bezug auf seine Größe berechnet.
Die Höhe eines Zahns wird durch das Modul (m) bestimmt.
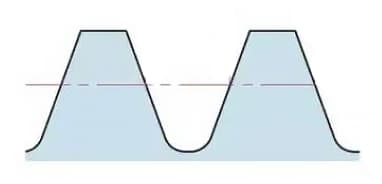
Die volle Zahnhöhe beträgt h=2,25m (= Kopfhöhe + Fußhöhe).
Die Profilhöhe (ha) ist die Höhe vom Zahnkopf bis zum Wälzkreis. ha=1m.
Die Fußhöhe (hf) ist die Höhe vom Zahnfuß bis zum Wälzkreis. hf=1,25m.
Der Bezugspunkt für die Dicke des Zahns (s) ist die halbe Teilung. s=πm/2.
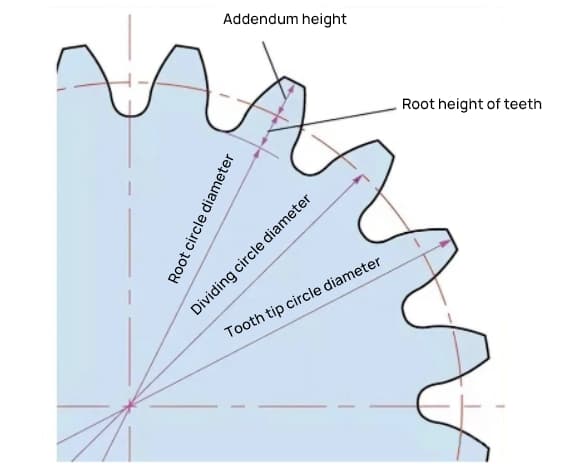
Der Parameter, der die Größe eines Zahnrads bestimmt, ist sein Teilkreisdurchmesser (d). Anhand des Teilkreises lassen sich die Teilung, Dicke, Höhe, Kopfhöhe und Fußhöhe des Zahnrads bestimmen.
Der Teilkreisdurchmesser ist d=zm.
Der Durchmesser des Kopfkreises ist da=d+2m.
Der Durchmesser des Kopfkreises beträgt df=d-2,5m.
Der Teilkreis ist nicht direkt auf dem eigentlichen Zahnrad zu sehen, da es sich um einen angenommenen Kreis handelt, der zur Bestimmung der Größe des Zahnrads verwendet wird.
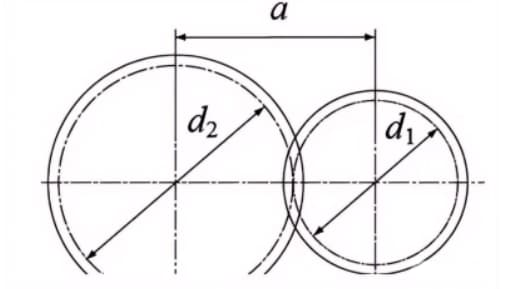
Wenn die Teilkreise eines Zahnradpaares tangential ineinandergreifen, ist die Achsabstand ist die Hälfte der Summe der Teilkreisdurchmesser.
Achsabstand a=(d1+d2)/2
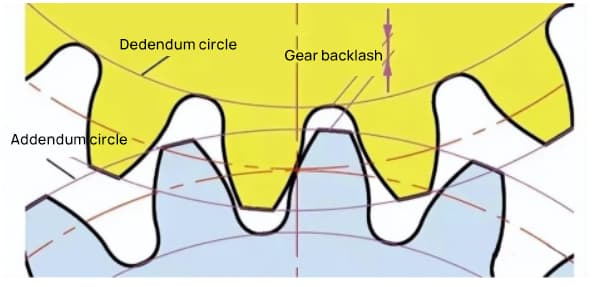
Das Spiel ist ein wichtiger Faktor für den reibungslosen Eingriff von Zahnrädern beim Einrücken. Es ist der Abstand zwischen den Zahnflächen, wenn ein Zahnradpaar im Eingriff ist.
Es gibt auch ein Spiel in Richtung der Zahnhöhe. Dieses Spiel wird als Axialspiel oder Spiel (c) bezeichnet. Das Spiel (c) ist die Differenz zwischen dem Fußkreisdurchmesser eines Zahnrades und dem Kopfkreisdurchmesser seines Gegenrades.
Freiraum c=1,25m-1m=0,25m
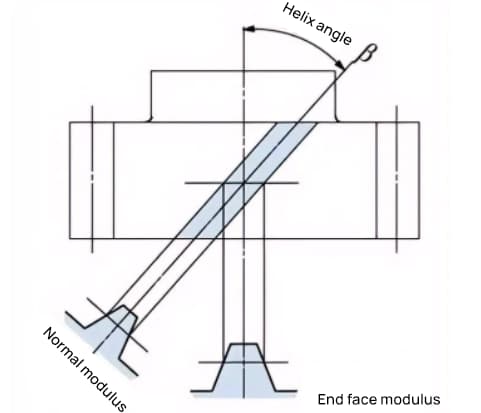
Ein Zahnrad, dessen Zähne nach einem Stirnrad spiralförmig verdreht sind, wird als Schrägstirnrad bezeichnet. Die meisten geometrischen Berechnungen für ein Stirnrad gelten auch für ein Schrägstirnrad. Es gibt zwei Arten von Schrägstirnrädern, die auf ihren Bezugsflächen basieren:
Bei schrägverzahnten Zahnrädern, wie z. B. Stirnrädern und Zykloidrädern, deren Zähne schraubenförmig sind, sind die Schrägungsrichtung und der Zahneingriff festgelegt.
Wenn die Achse des Zahnrads nach oben und unten zeigt, ist die Richtung der Zähne nach rechts oben als "rechts" und nach links oben als "links", wenn man sie von vorne betrachtet. Das Ineinandergreifen der verschiedenen Zahnradtypen ist unten dargestellt.
Werden Zähne mit gleichem Abstand nur am äußeren Umfang des Reibrades unterteilt, mit Vorsprüngen versehen und dann miteinander verzahnt und gedreht, können folgende Probleme auftreten:
Wenn die Getriebeübersetzung sowohl leise als auch sanft sein soll, werden Evolventenkurven verwendet.
Eine Evolventenkurve ist eine Kurve, die man erhält, indem man einen Draht mit einem Bleistift auf den äußeren Umfang eines Zylinders wickelt und den Draht in gespanntem Zustand allmählich loslässt.
Die mit dem Bleistift gezeichnete Kurve ist die Evolventenkurve, und der äußere Umfang des Zylinders wird als Grundkreis bezeichnet.
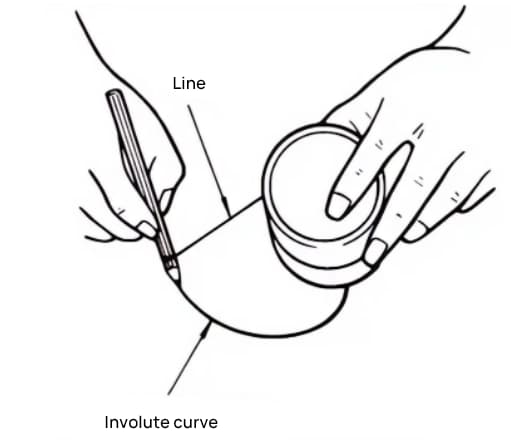
Teile den Zylinder in 8 gleiche Teile und binde 8 Bleistifte daran, um 8 Evolventenkurven zu zeichnen. Wickeln Sie dann die Drähte in die entgegengesetzte Richtung und zeichnen Sie 8 weitere Kurven nach der gleichen Methode. Dies ist ein Zahnrad mit 8 Zähnen und Evolventenkurven als Zahnprofil.
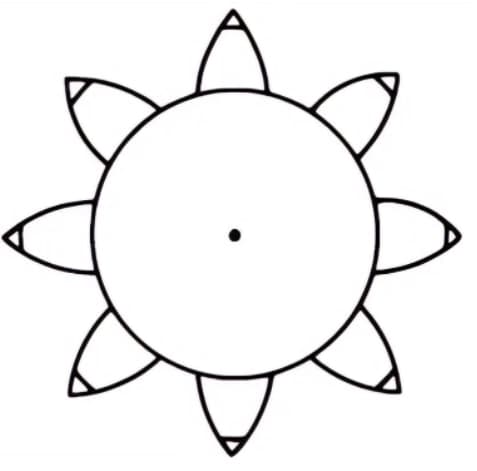
Zu den Vorteilen von Evolventenrädern gehören die Fähigkeit, ein konstantes Übersetzungsverhältnis zu übertragen, der reibungslose Betrieb aufgrund des sich allmählich verändernden Tragbildes und die geringe Empfindlichkeit gegenüber Achsabstandsschwankungen.
Der Grundkreis ist der Grundkreis, der das Evolventen-Zahnprofil bildet. Der Teilkreis ist der Bezugskreis, der die Größe des Zahnrads bestimmt. Der Grundkreis und der Teilkreis sind wichtige geometrische Abmessungen von Zahnrädern.
Das Evolventen-Zahnprofil ist eine Kurve, die auf der Außenseite des Grundkreises gebildet wird, und der Eingriffswinkel auf dem Grundkreis ist Null.
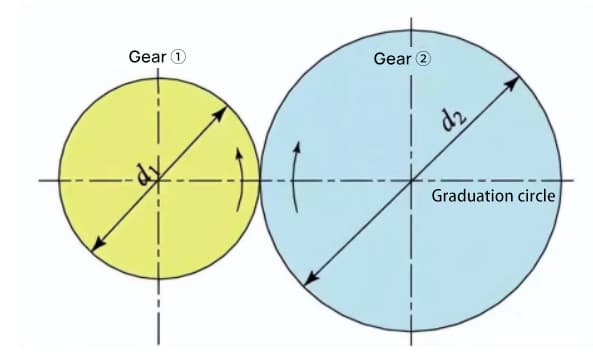
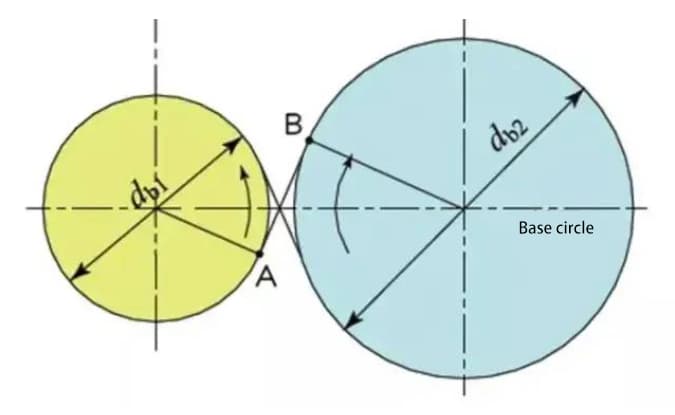
Wenn zwei Standard-Evolventenräder miteinander kämmen, sind ihre Teilkreise im Standard-Achsabstand tangential zueinander. Der Eingriff der beiden Zahnräder sieht aus wie die Übertragung von zwei Reibrädern mit den Durchmessern d1 bzw. d2.
Die Verzahnung von Evolventenrädern hängt jedoch eher vom Grundkreis als vom Teilkreis ab.
Die Kontaktpunkte zwischen den ineinander greifenden Zähnen zweier Zahnräder bewegen sich entlang der Wirkungslinie in der Reihenfolge P1, P2 und P3.
Achten Sie auf den gelben Zahn des Antriebsrads. Nachdem dieser Zahn zu kämmen beginnt, befindet sich das Zahnrad für eine gewisse Zeit in einem Zustand des Zweizahneingriffs (P1, P3). Der Eingriff setzt sich fort, und wenn sich der Kontaktpunkt zum Punkt P2 auf dem Teilkreis bewegt, ist nur noch ein Zahn im Eingriff.
Der Zahneingriff wird fortgesetzt, und wenn sich der Kontaktpunkt zum Punkt P3 bewegt, beginnt der nächste Zahn des Zahnrads am Punkt P1 zu kämmen, wodurch wieder ein Zweizahneingriff entsteht. Auf diese Weise wirken der Zweizahneingriff und der Einzelzahneingriff der Zahnräder zusammen und übertragen wiederholt eine Drehbewegung.
Die gemeinsame Tangente zwischen den Grundkreisen A-B wird als Wirkungslinie bezeichnet. Die Berührungspunkte der Zahnradpaare liegen alle auf dieser Wirkungslinie.
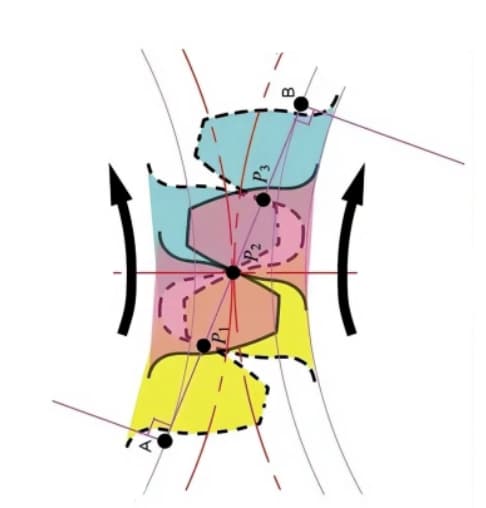
Zur Veranschaulichung: Es handelt sich um einen Riemen, der an den äußeren Rändern zweier Grundkreise verläuft und durch Drehbewegung Energie überträgt.
Das Zahnprofil der von uns verwendeten Zahnräder ist in der Regel eine Standardevolvente, aber es gibt auch Situationen, in denen die Zähne des Zahnrads verschoben werden müssen, z. B. um den Achsabstand anzupassen oder ein Unterschneiden des kleineren Zahnrads zu verhindern.
Die evolventische Zahnformkurve variiert mit der Anzahl der Zähne. Je mehr Zähne vorhanden sind, desto mehr tendiert die Zahnformkurve zu einer geraden Linie.
Mit zunehmender Anzahl der Zähne wird die Zahnfußform dicker, und die Festigkeit des Zahnrads nimmt zu.
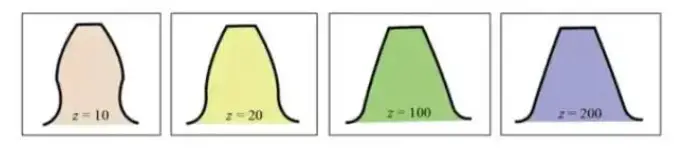
Aus dem obigen Diagramm ist ersichtlich, dass bei einem Zahnrad mit 10 Zähnen ein Teil des Evolventen-Zahnprofils am Zahnfuß entfernt wird, was zu einer Unterschneidung führt.
Durch die Annahme einer positiven Verschiebung für das Zahnrad mit z=10, die Vergrößerung des Kopfkreisdurchmessers und die Vergrößerung der Zahndicke der Zahnradzähne kann jedoch die gleiche Zahnradfestigkeit wie bei einem Zahnrad mit 200 Zähnen erreicht werden.
Die folgende Abbildung zeigt die schematische Darstellung eines Zahnrads mit 10 Zähnen und positiver Verschiebung. Beim Verzahnen wird der Betrag der Werkzeugbewegung entlang der radialen Richtung als radialer Verschiebungsbetrag xm(mm) bezeichnet.
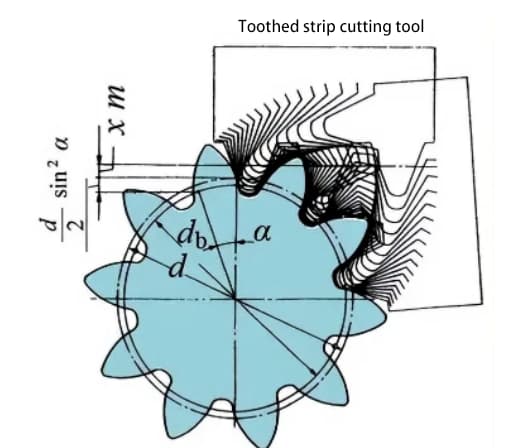
Durch die positive Verschiebung des Zahnprofils vergrößert sich die Zahndicke des Zahnrades und der Außendurchmesser (Kopfkreisdurchmesser) nimmt ebenfalls zu.
Durch eine positive Verdrängung kann ein Unterschneiden der Zahnräder vermieden werden. Die Verdrängung von Zahnrädern kann auch andere Zwecke erfüllen, wie z. B. die Änderung des Achsabstands. Durch eine positive Verdrängung kann der Achsabstand vergrößert, durch eine negative Verdrängung verkleinert werden.
Unabhängig davon, ob es sich um ein Getriebe mit positiver oder negativer Verdrängung handelt, gibt es Grenzen für den Verdrängungsbetrag.
Die Verschiebung kann positiv oder negativ sein. Obwohl die Zahnhöhe gleich ist, ist die Zahndicke unterschiedlich. Ein Zahnrad mit verdickter Zahndicke ist ein Rad mit positiver Verdrängung, während ein Rad mit reduzierter Zahndicke ein Rad mit negativer Verdrängung ist.
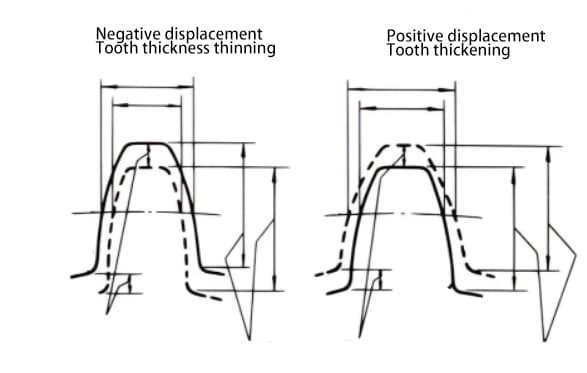
Wenn es nicht möglich ist, den Achsabstand zwischen zwei Zahnrädern zu ändern, kann eine positive Verschiebung auf das kleinere Zahnrad angewendet werden (um ein Unterschneiden zu vermeiden) und eine negative Verschiebung auf das größere Zahnrad, um den gleichen Achsabstand zu erreichen. In diesem Fall ist der absolute Wert des Verschiebungsbetrags gleich.
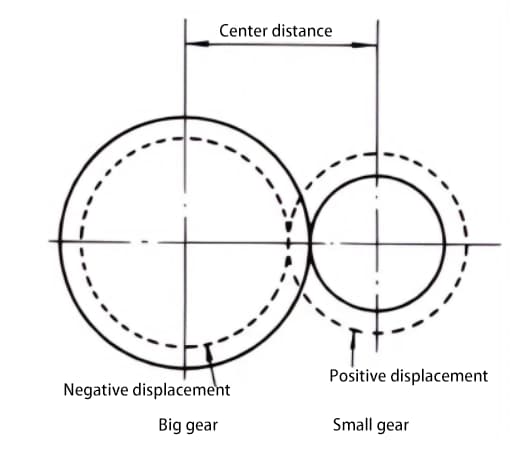
Standardzahnräder greifen ineinander, wenn ihre Teilkreise tangential zueinander sind. Der Zahneingriff von verschobenen Zahnrädern, wie in der Abbildung dargestellt, ist tangential zueinander auf dem Eingriffskreis.
Der Eingriffswinkel auf dem Eingriffskreis wird als Eingriffswinkel bezeichnet. Der Eingriffswinkel unterscheidet sich vom Eingriffswinkel auf dem Teilkreis (Teilkreis-Eingriffswinkel) und ist ein wichtiger Faktor bei der Auslegung von verschobenen Zahnrädern.
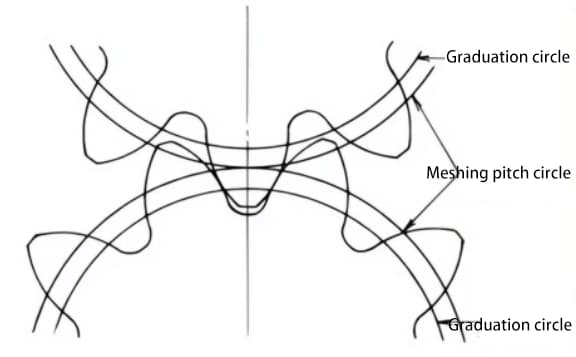
Die Verschiebung des Zahnrads kann Unterschneidungen verhindern, die durch eine geringe Anzahl von Zähnen während der Bearbeitung verursacht werden. Der gewünschte Achsabstand kann durch Verschiebung erreicht werden.
Bei einem Zahnradpaar mit einem großen Unterschied in der Anzahl der Zähne kann eine positive Verschiebung auf das leichter abgenutzte kleinere Zahnrad angewandt werden, um die Zahndicke zu erhöhen, während eine negative Verschiebung auf das größere Zahnrad angewandt werden kann, um die Zahndicke zu verringern, um die Lebenserwartung der beiden Zahnräder vergleichbarer zu machen.
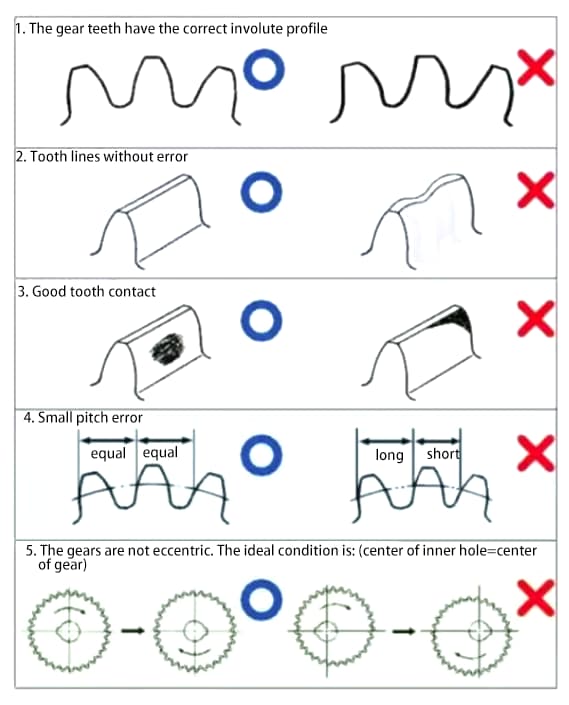
Zahnräder sind mechanische Bauteile, die Kraft und Drehung übertragen. Die wichtigsten Anforderungen an die Leistung von Getrieben sind:
Um den oben genannten Anforderungen gerecht zu werden, ist die Verbesserung der Verzahnungsgenauigkeit eine notwendige Aufgabe.
Die Genauigkeit von Zahnrädern lässt sich grob in drei Kategorien einteilen:
a) Genauigkeit des Evolventen-Zahnprofils - Zahnprofilgenauigkeit
b) Genauigkeit der Zahnflankenlinie auf der Zahnoberfläche - Zahnliniengenauigkeit
c) Genauigkeit der Position der Zähne/Schlitze.
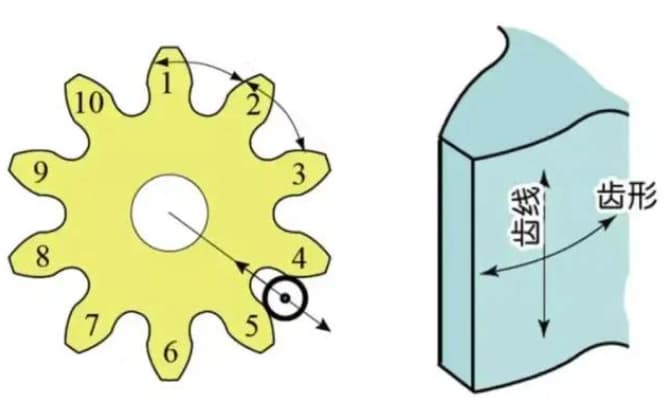
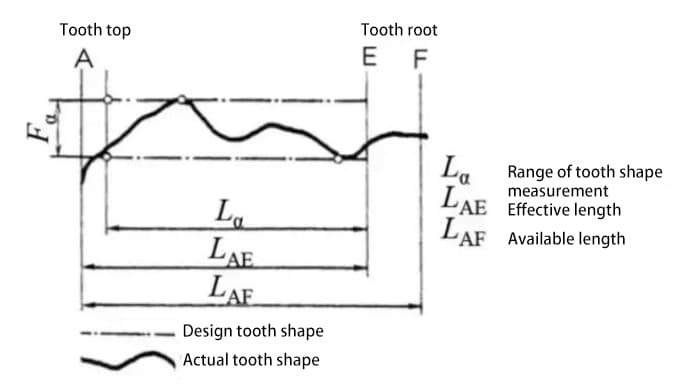
Der Zahnprofilfehler ist der Fehler zwischen dem tatsächlichen Zahnprofil des Zahnrads und dem theoretischen Zahnprofil.
Es gibt viele Faktoren, die den Zahnprofilfehler beeinflussen, wie z.B. das Werkzeug und die Vibrationen der Werkzeugmaschine während des Schneidprozesses.
Der Zahnprofilfehler wirkt sich auf die Verzahnungsleistung und die Geräuschentwicklung aus. Daher ist es notwendig, den Zahnprofilfehler innerhalb des zulässigen Bereichs zu kontrollieren.
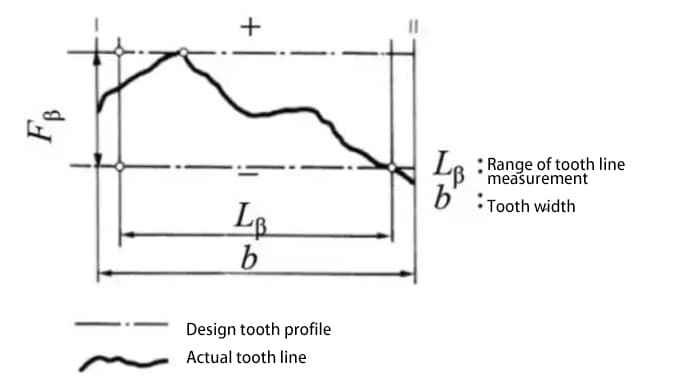
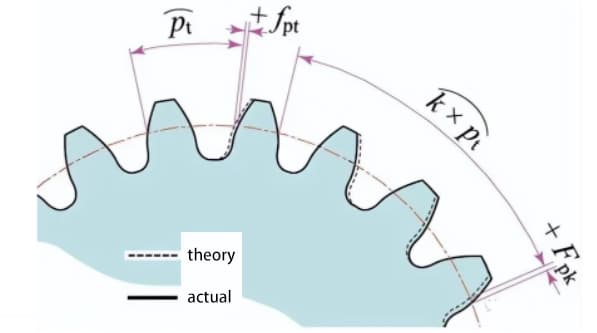
Messen Sie den Teilungswert am Messumfang zentriert auf der Getriebewelle.
Die Einzelzahnteilungsabweichung (fpt) ist die Differenz zwischen der tatsächlichen und der theoretischen Teilung.
Die kumulierte Gesamtteilungsabweichung (Fp) wird zur Bewertung der Abweichung der gesamten Zahnradteilung verwendet. Der Gesamtamplitudenwert der Kurve der kumulativen Steigungsabweichung stellt die gesamte Steigungsabweichung dar.
Setzen Sie einen Tastkopf (kugelförmig oder zylindrisch) nacheinander in die Verzahnungsnut und messen Sie die Differenz zwischen dem maximalen und dem minimalen radialen Abstand des Tastkopfs zur Zahnradachse. Die Exzentrizität der Getriebewelle ist einer der Faktoren, die zur Rundlaufabweichung beitragen.
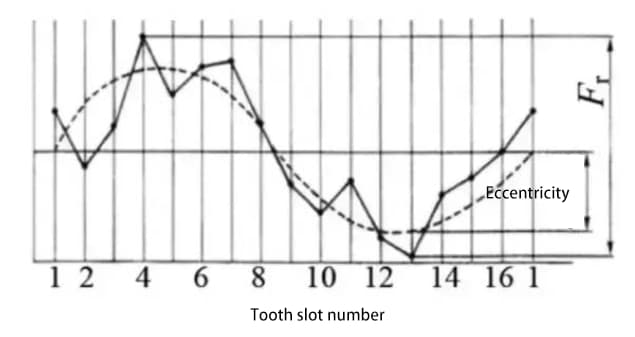
Die bisher beschriebenen Methoden zur Bewertung der Genauigkeit von Zahnrädern, wie Zahnform, Teilung und Zahnflankengenauigkeit, sind allesamt Methoden zur Bewertung der Genauigkeit eines einzelnen Zahnrades.
Im Gegensatz dazu gibt es eine andere Methode, bei der die Genauigkeit des Zahnrads bewertet wird, indem das Zahnrad in Kombination mit einem Messzahnrad einem Zweizahn-Eingriffstest unterzogen wird. Die beiden Flächen des geprüften Zahnrads greifen in das Messzahnrad ein und drehen sich einen ganzen Zyklus lang. Die Änderung des Achsabstands wird aufgezeichnet.
Die folgende Abbildung zeigt die Prüfergebnisse für ein Zahnrad mit 30 Zähnen. Es gibt insgesamt 30 Wellenlinien für die radiale Verbundabweichung eines einzelnen Zahns.
Der Wert der radialen Verbundabweichung ist ungefähr die Summe aus Rundlaufabweichung und radialer Verbundabweichung des Einzelzahns.
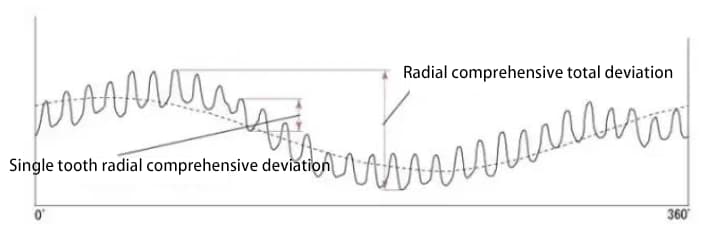
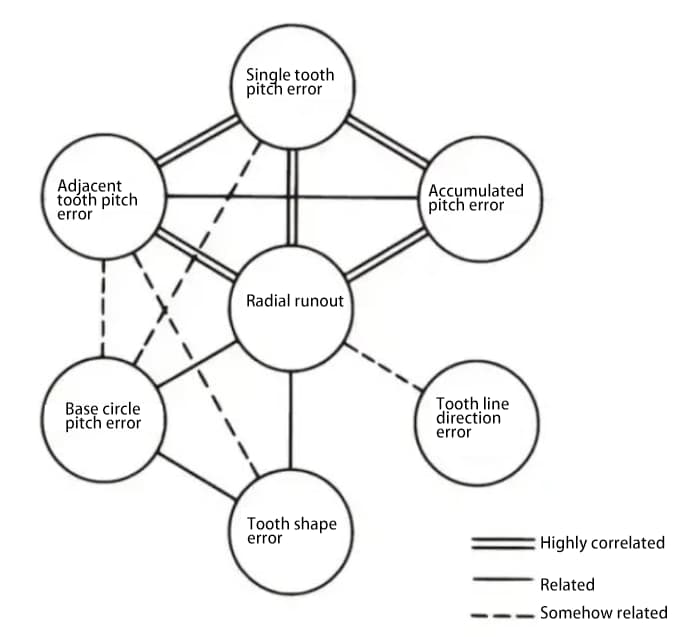
Die verschiedenen Teile der Verzahnungsgenauigkeit stehen in Beziehung zueinander. Im Allgemeinen ist die Rundlaufabweichung stark mit anderen Fehlern korreliert, und auch zwischen den verschiedenen Teilungsfehlern besteht eine starke Korrelation.
Spiralwinkel an einem normalen zylindrischen Abschnitt:
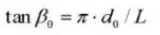
Spiralwinkel auf einem Basiszylinder:
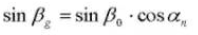
Zahndicke Zentrierwinkel:
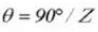
Durchmesser der Stifte:
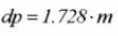
Korrekturfaktor für den Achsabstand:
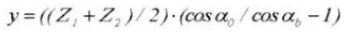
Berechnung von Standard-Stirnrädern (Ritzel ①, Zahnrad ②)
1. Anzahl der Zähne am Zahnrad Standard
2. Standard Evolventenverzahnung Profil Geradverzahnung
3. Modul m
4. Eingriffswinkel
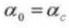
5. Anzahl von Zähnen
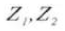
6. Effektive Zahntiefe
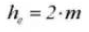
7. Gesamte Tiefe des Zahns
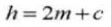
8. Zahnradspiel
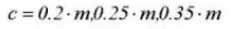
9. Referenz-Teilkreisdurchmesser
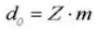
10. Außendurchmesser
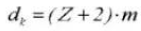
11. Wurzel-Durchmesser
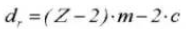
12. Grundkreis-Durchmesser
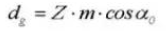
13. Kreisförmige Teilung
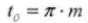
14. Normale Diametrale Teilung
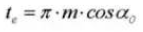
15. Kreiszahndicke
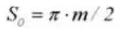
16. Dicke der Sehnenzähne
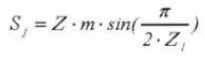
17. Zahnhöhe des Getriebeölmessstabs
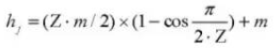
18. Anzahl der Zähne quer
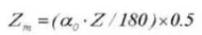
19. Zahndicke quer
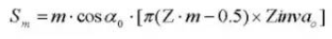
20. Stiftdurchmesser
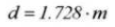
21. Zylindrisches Messmaß
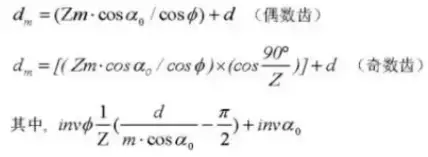
Formel zur Berechnung von verschobenen Stirnrädern (Ritzel ①, Zahnrad ②):
1. Zahnradprofil quer
2. Kontaktverhältnis des Werkzeugzahnprofils
3. Modul m
4. Eingriffswinkel
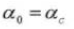
5. Anzahl der Zähne Z
6. Effektive Zahntiefe
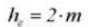
7. Gesamte Tiefe des Zahns
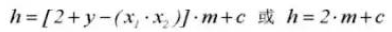
8. Getriebespiel C
9. Traganteil in Querrichtung X
10. Achsabstand
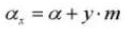
11. Referenz-Teilkreisdurchmesser
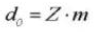
12. Betriebsdruckwinkel
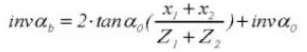
13. Teilkreisdurchmesser
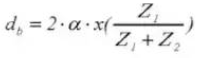
14. Außendurchmesser
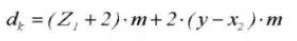
15. Nachtragsdurchmesser
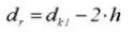
16. Teilungsdurchmesser
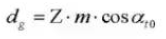
17. Kreisförmige Teilung
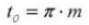
18. Normale Diametrale Teilung
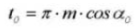
19. Kreiszahndicke
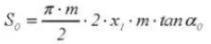
20. Dicke der Sehnenzähne
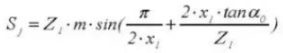
21. Zahnradmessschieber Zahnhöhe
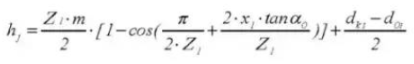
22. Anzahl der Zähne über
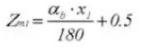
23. Zahndicke quer
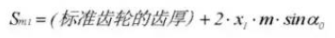
24. Durchmesser der Spitze
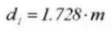
25. Transversales Messmaß
Formel für die Berechnung von Standard-Schrägverzahnungen (normales System) (Ritzel ①, Zahnrad ②)
1. Zahnradprofil Standard
2. Referenzabschnitt des Zahnprofils Normales System
3. Werkzeug Zahnprofil Schrägverzahnung
4. Modul
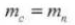
5. Eingriffswinkel
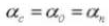
6. Anzahl der Zähne
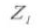
7. Helix-Richtung
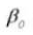
8. Effektive Zahntiefe
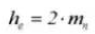
9. Gesamte Tiefe des Zahns
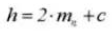
10. Vorderer Eingriffswinkel
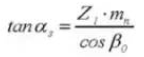
11. Achsabstand
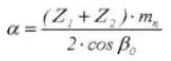
12. Referenz-Teilkreisdurchmesser
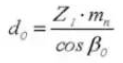
13. Außendurchmesser
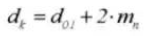
14. Wurzel-Durchmesser
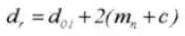
15. Teilungsdurchmesser
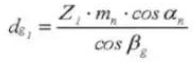
16. Helix-Winkel auf dem Grundkreis
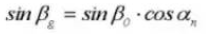
17. Stellplatz
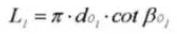
18. Kreisförmige Teilung (Normales System)
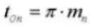
19. Normaler diametraler Abstand (normales System)
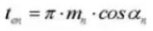
20. Kreisförmige Zahndicke (Normales System)
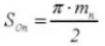
21. Äquivalente Anzahl von Zähnen an einem Standard-Stirnradgetriebe
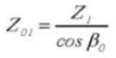
22. Dicke der Sehnenzähne
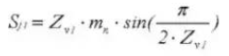
23. Zahnradmessschieber Zahnungstiefe
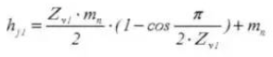
24. Anzahl der Zähne quer
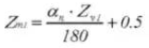
25. Zahndicke quer
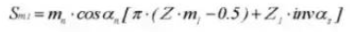
26. Durchmesser der Spitze
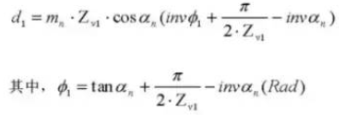
27. Zylindrisches Messmaß
28. Getriebespiel f
Formel zur Berechnung von verschobenen Stirnrädern (normales System) (Ritzel ①, Zahnrad ②):
1. Zahnradprofil verschoben
2. Referenzabschnitt des Zahnprofils Normales System
3. Werkzeug Zahnprofil Schrägverzahnung
4. Modul (Normales System)
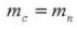
5. Druckwinkel (normales System)
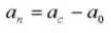
6. Anzahl der Zähne
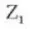
7. Helix-Richtung
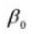
8. Effektive Zahntiefe
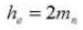
9. Gesamte Tiefe des Zahns
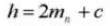
10. Traganteil in Querrichtung
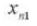
11. Achsabstand
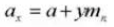
12. Normales Modul
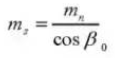
13. Vorderer Eingriffswinkel (normales System)
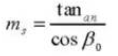
14. Äquivalente Anzahl von Zähnen an einem Standard-Stirnradgetriebe
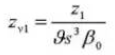
15. Normaler Systemdruckwinkel
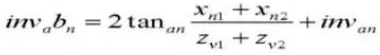
16. Referenz-Teilkreisdurchmesser
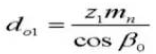
17. Außendurchmesser
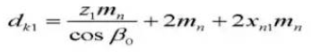
18. Teilungsdurchmesser der Zähne in Kontakt
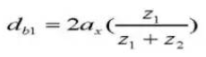
19. Teilungsdurchmesser
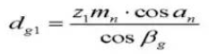
20. Helix-Winkel am Basiszylinder
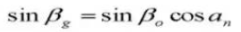
21. Kreiszahndicke
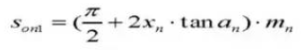
22. Dicke der Sehnenzähne
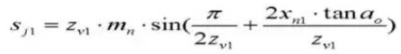
23. Zahnradmessschieber Zahnhöhe.
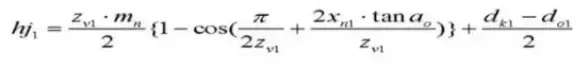
24. Anzahl der Zähne quer
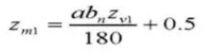
25. Zahndicke quer
26. Stift-Durchmesser.
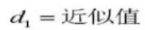
27. Zylindrisches Messmaß
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
AR 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO