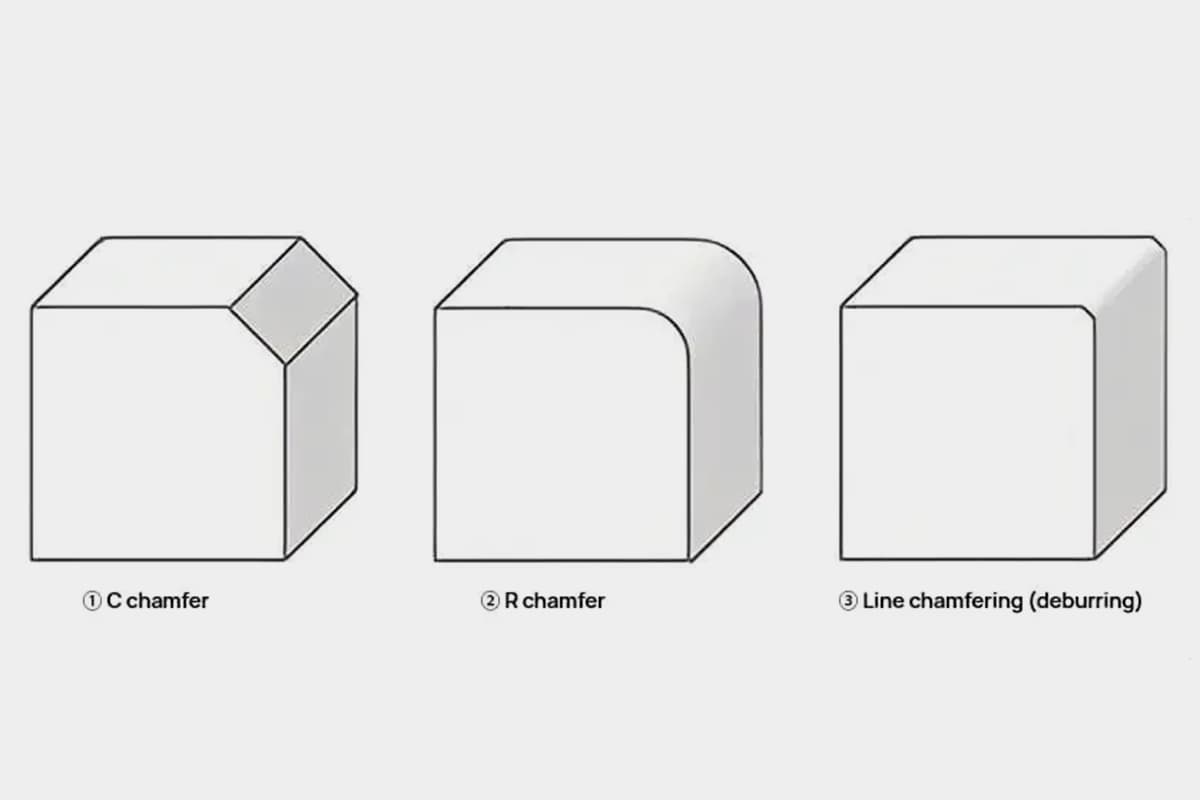
Haben Sie sich jemals gefragt, wie Ingenieure Präzision und Genauigkeit in der Fertigung sicherstellen? In diesem Blogbeitrag tauchen wir in die faszinierende Welt der geometrischen Toleranzen ein - ein entscheidender Aspekt des Maschinenbaus, der die Herstellung hochwertiger Komponenten ermöglicht. Auf der Grundlage des Fachwissens erfahrener Experten werden wir die verschiedenen Arten von Toleranzen und ihre Anwendungen untersuchen und Ihnen wertvolle Einblicke geben, um Ihr Verständnis für dieses komplexe Thema zu verbessern. Machen Sie sich bereit, die Geheimnisse der Perfektion im Bereich des Maschinenbaus zu entdecken!
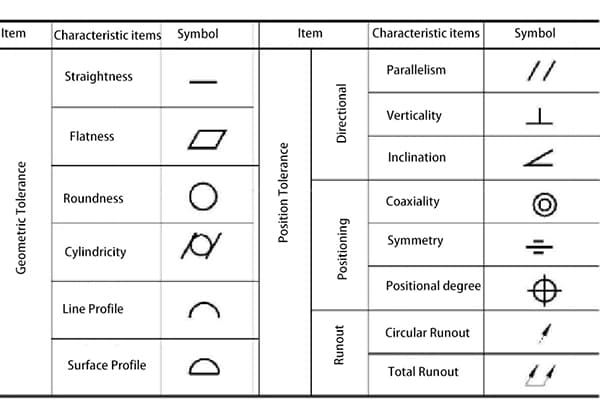
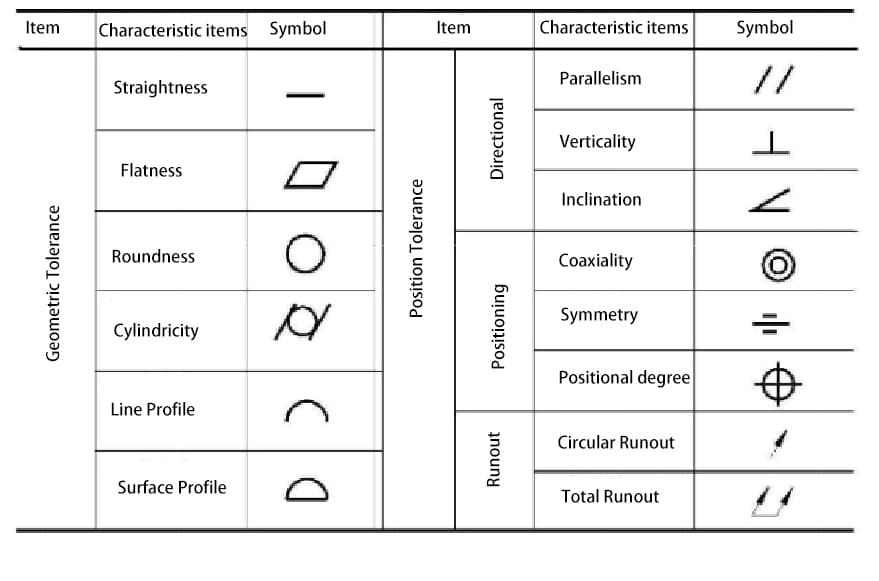
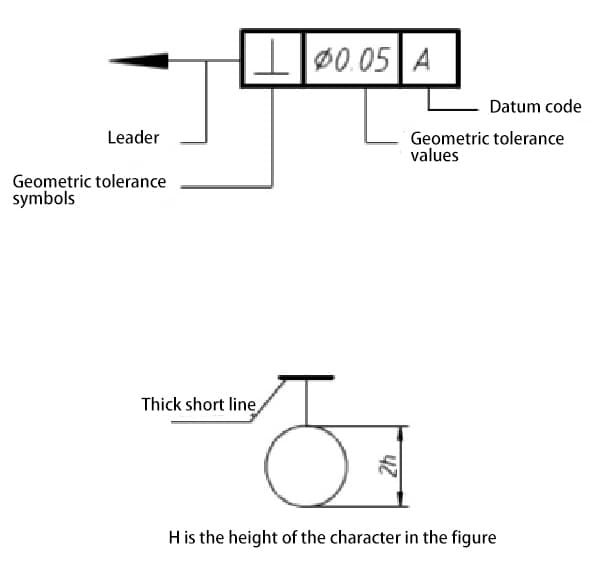
Die in der nationalen Norm festgelegte geometrische Toleranz ist in zwei Kategorien unterteilt: geometrische Toleranz und Positionstoleranz, insgesamt 14 Positionen.
Ihre Namen und Symbole sind in der nachstehenden Tabelle aufgeführt.
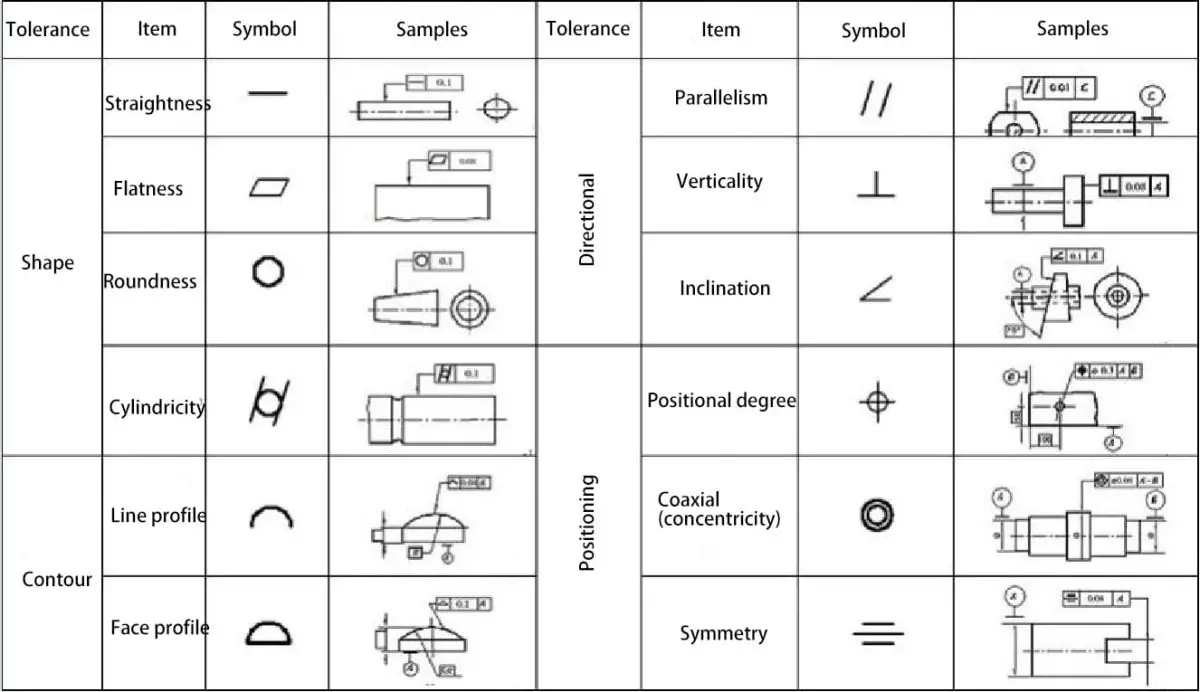
Geradheit - Alle Punkte liegen auf einer geraden Linie, wobei die Toleranz durch den Bereich zwischen zwei parallelen Linien bestimmt wird.
Ebenheit - Alle Punkte auf einer Fläche liegen auf einer Ebene, wobei die Toleranz durch den Bereich zwischen zwei parallelen Ebenen bestimmt wird.
Rundheit - Alle Punkte auf einer Fläche liegen auf einem Kreisumfang, wobei die Toleranz durch den Bereich zwischen zwei konzentrischen Kreisen bestimmt wird.
Zylindrizität - Die Achsen aller Punkte auf einer rotierenden Fläche sind gleich weit von einer gemeinsamen Achse entfernt. Die Zylindrizitätstoleranz definiert den Toleranzbereich, der von zwei konzentrischen Zylindern gebildet wird, wobei die rotierende Fläche innerhalb dieses Bereichs liegen muss.
Profil-Toleranz - Definiert die Toleranzmethode für unregelmäßige Flächen, Linien, Bögen oder gewöhnliche Ebenen. Das Profil kann auf ein einzelnes Linienelement oder die gesamte Oberfläche eines Teils angewendet werden. Die Profiltoleranz gibt die eindeutige Begrenzung entlang des tatsächlichen Profils an.
Rechtwinkligkeit - Die Fläche oder Achse steht senkrecht zur Bezugsebene oder -achse. Die Rechtwinkligkeitstoleranz gibt eine der folgenden Möglichkeiten an: den Bereich, der durch zwei Ebenen senkrecht zur Bezugsebene oder -achse definiert ist, oder den Bereich, der durch zwei parallele Ebenen senkrecht zur Bezugsachse definiert ist.
Parallelität - Die Fläche oder Achse und alle Punkte sind gleich weit von der Bezugsebene oder -achse entfernt. Parallelitätstoleranz gibt eine der folgenden Möglichkeiten an: den Bereich, der durch zwei parallele Ebenen oder Linien parallel zur Bezugsebene oder -achse definiert ist, oder den Bereich der Zylindertoleranz, in dem die Achse parallel zur Bezugsachse verläuft.
Koaxialität - Die Achse aller sich schneidenden kombinierbaren Elemente der Drehfläche ist die gemeinsame Achse des Daten-Features. Die Koaxialitätstoleranz gibt den Toleranzbereich der Zylindrizität an, in dem die Achse mit der Bezugsachse übereinstimmt.
Positionstoleranz - Die Positionstoleranz definiert den Bereich, in dem die Mittelachse oder die Mittelebene von der tatsächlichen (theoretisch richtigen) Position abweichen darf.
Das Grundmaß legt die tatsächliche Position zwischen dem Datenmerkmal und dem verknüpften Merkmal fest. Der Positionsfehler ist die gesamte zulässige Positionsabweichung zwischen dem Merkmal und seiner korrekten Position.
Bei zylindrischen Merkmalen wie Bohrungen und Außendurchmessern ist die Positionstoleranz normalerweise der Durchmesser des Toleranzbereichs, in den die Achse des Merkmals fallen muss. Bei nicht kreisförmigen Merkmalen (wie Nuten und kurzen Vorsprüngen) ist die Positionstoleranz die Gesamtbreite des Toleranzbereichs, in den die Mittelebene des Merkmals fallen muss.
Rundlaufgenauigkeit - Ermöglicht die Kontrolle über kreisförmige Oberflächenelemente. Wenn sich das Teil um 360 Grad dreht, wird diese Toleranz unabhängig an jeder Messposition des kreisförmigen Elements angewendet und auf die Rundlauftoleranz angewandt, die um die Bezugsachse herum konstruiert wurde, wodurch die kumulierte Änderung der Rundheit und Koaxialität kontrolliert wird.
Bei Anwendung auf eine Fläche, die vertikal mit der Bezugsachse konstruiert ist, steuert sie kreisförmige Elemente von ebenen Flächenelementen.
Gesamtauslauf - Bietet eine zusammengesetzte Kontrolle über alle Oberflächenelemente. Wenn sich das Teil um 360 Grad dreht, wird diese Toleranz gleichzeitig auf runde und längliche Merkmale angewendet. Bei Anwendung auf eine Oberfläche, die um die Bezugsachse konstruiert ist, steuert der Gesamtrundlauf die kumulierte Variabilität der Rundheit und Zylindrizität, GeradheitKoaxialität, Winkel, Konizität und Profil. Bei Anwendung auf eine Fläche, die senkrecht zur Bezugsachse konstruiert ist, kontrolliert sie die kumulierte Variabilität von Rechtwinkligkeit und Geradheit.
Feature - bezieht sich auf die Punkte, Linien und Flächen, aus denen die Geometrie einer Komponente besteht.
Ideales Merkmal - ein Merkmal mit geometrischer Bedeutung.
Tatsächliches Merkmal - das Merkmal, das tatsächlich an der Komponente vorhanden ist, in der Regel dargestellt durch ein gemessenes Merkmal.
Bezugsmerkmal - ein Merkmal, das zur Bestimmung der Richtung oder Position des gemessenen Merkmals verwendet wird. Einfach als Referenz bezeichnet, dient es als Grundlage für die Bestimmung der geometrischen Beziehung zwischen Merkmalen. Dazu gehören Referenzpunkte, Referenzlinien und Referenzflächen.
Gemessenes Feature - das Feature, das die Form- oder Positionstoleranz angibt.
Zentrales Merkmal - Punkte, Linien oder Flächen, die eine symmetrische Beziehung zum Merkmal haben.
Toleranzband - schränkt die Variation der tatsächlichen Form- oder Positionsmerkmale ein. Es ist ein Bereich, der durch einen bestimmten maximalen Fehlerwert definiert ist, der durch Größe, Form, Richtung und Position bestimmt wird.
Das Toleranzband ist der Bereich zwischen zwei parallelen Linien/Ebenen/Zylindern usw. im Abstand des Toleranzwertes t
Beispiel 1
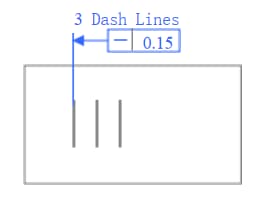
Jede eingravierte Linie muss sich zwischen zwei parallelen Linien auf der Oberfläche mit einer Toleranz von 0,015 mm befinden.
Beispiel 2
Jede Elementlinie auf der zylindrischen Oberfläche muss sich innerhalb der axialen Ebene und zwischen zwei parallelen Linien mit einem Abstand von 0,02 mm befinden.
Anwendungsbeispiel
Beispiel 3
Jede Elementlinie auf der zylindrischen Oberfläche muss sich innerhalb der axialen Ebene und zwischen zwei parallelen Linien mit einer Toleranz von 0,04 mm innerhalb von 100 mm befinden.
Beispiel 4
Diskussion: Wie ist es zu verstehen, wenn auf derselben Fläche in zwei Richtungen unterschiedliche Geradheitstoleranzen angegeben sind?
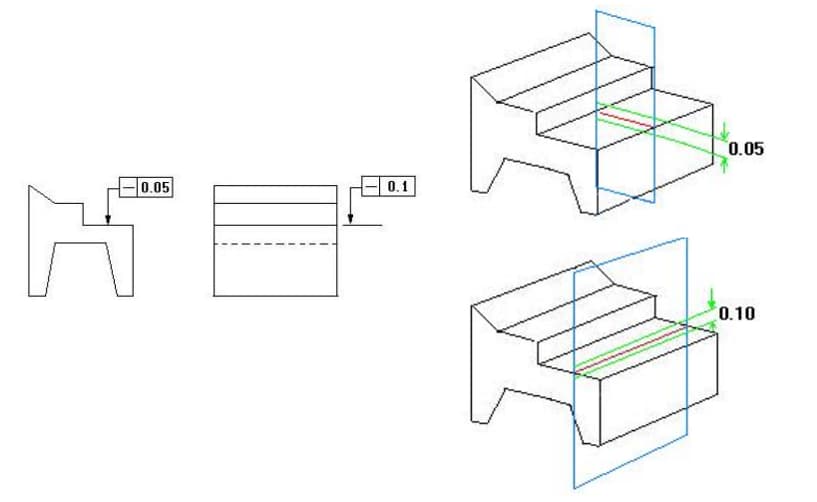
Das Toleranzband ist der Bereich zwischen zwei parallelen Ebenen in einem Abstand des Toleranzwertes t.
Sie stellt die tatsächliche Form der ebenen Merkmale des Bauteils unter Beibehaltung der idealen ebenen Bedingung dar.
Beispiel 1
Die obere Fläche muss innerhalb zweier paralleler Ebenen mit einer Toleranz von 0,1 mm liegen.
Beispiel 2
Jeder 100×100-Bereich auf der Oberfläche muss sich innerhalb zweier paralleler Ebenen mit einer Toleranz von 0,1 mm befinden.
Er stellt die tatsächliche Form des kreisförmigen Merkmals auf dem Bauteil dar, wobei sein Mittelpunkt einen gleichmäßigen Abstand einhält.
Das Toleranzband ist der Bereich zwischen zwei konzentrischen Kreisen mit einem Radiusunterschied des Toleranzwertes t auf demselben Querschnitt.
Beispiel 1
In jedem Querschnitt senkrecht zur Achse muss sich der Kreis zwischen zwei konzentrischen Kreisen mit einem Radius von 0,02 mm befinden.
Beispiel 2
In jedem Querschnitt senkrecht zur Achse muss sich der Kreis zwischen zwei konzentrischen Kreisen mit einem Radius von 0,02 mm befinden.
Sie stellt den Zustand dar, bei dem alle Punkte auf der Kontur der zylindrischen Oberfläche des Bauteils den gleichen Abstand zu seiner Achse haben.
Das Toleranzband ist der Bereich zwischen zwei zylindrischen Flächen mit einem Radiusunterschied des Toleranzwertes t auf derselben Achse.
Beispiel 1
Die zylindrische Fläche muss sich zwischen zwei zylindrischen Flächen mit einem Radiusunterschied von 0,05 mm auf derselben Achse befinden.
Er stellt den Zustand dar, bei dem das tatsächlich gemessene Merkmal auf dem Bauteil den gleichen Abstand zur Referenz einhält.
Bei einer Richtung ist das Toleranzband der Bereich zwischen zwei parallelen Ebenen im Abstand des Toleranzwertes t und parallel zur Bezugsebene (oder Linie, Achse); bei zwei senkrechten Richtungen ist es der Bereich innerhalb eines rechteckigen Prismas mit den Abmessungen der Toleranzwerte t1×t2 und parallel zur Bezugsachse.
Beispiel 1
Die Oberseite muss sich zwischen zwei parallelen Ebenen mit einem Abstand von 0,05 mm und parallel zur Bezugsebene befinden.
Beispiel 2
Die Achse von ΦD muss sich zwischen zwei parallelen Ebenen im Abstand des Toleranzwertes 0,1 mm und senkrecht parallel zur Bezugsachse Φ befinden.
Die Toleranz stellt den Zustand dar, bei dem das tatsächliche Feature auf dem Teil in einem korrekten 90-Grad-Winkel relativ zum Referenz-Feature gehalten wird.
Wenn eine Richtung angegeben wird, ist die Toleranzzone der Bereich zwischen zwei parallelen Ebenen (oder Linien), die senkrecht zur Bezugsebene (oder Linie, Achse) liegen und einen Abstand haben, der dem Toleranzwert t entspricht.
Sind zwei zueinander senkrechte Richtungen angegeben, so ist die Toleranzzone der Bereich innerhalb eines Parallelepipeds mit den Abmessungen t1 × t2, der senkrecht zur Bezugsachse liegt.
Beispiel 1
Die rechte Fläche muss zwischen zwei parallelen Ebenen liegen, die senkrecht zur Bezugsebene verlaufen und eine Abweichung von 0,05 mm aufweisen.
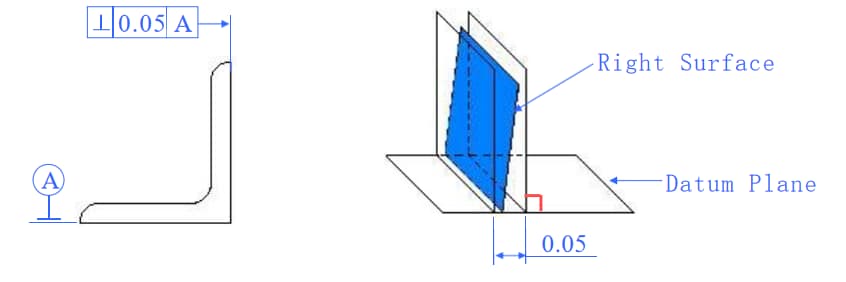
Beispiel 2
Die linke Fläche muss innerhalb einer Abweichungsspanne von 0,05 mm und zwischen zwei parallelen Ebenen liegen, die senkrecht zur Bezugsachse verlaufen.
Beispiel 3
Die Achse des Zylinders d muss innerhalb der Zylinderoberfläche senkrecht zur Bezugsebene mit einer Durchmessertoleranz von 0,05 mm liegen.
Beispiel 4
Die Achse des kreisförmigen Lochs E muss zwischen zwei parallelen Ebenen liegen, die senkrecht zur Bezugsebene Z stehen, mit einer Abweichung von 0,06 mm.
Korrekter Zustand von zwei Elementen auf dem Teil, das einen bestimmten Winkel zwischen ihren relativen Richtungen einhält.
Innerhalb einer bestimmten Richtung ist die Toleranzzone die Fläche zwischen zwei parallelen Ebenen (oder Linien), die in einem theoretisch richtigen Winkel zur Bezugsebene (oder Linie oder Achse) und in einem Abstand des Toleranzwerts t von ihr liegen.
Beispiel 1
Die geneigte Fläche muss sich zwischen zwei parallelen Ebenen befinden, die in einem Winkel von 45 Grad zur Bezugsebene und in einem Abstand von 0,08 mm von dieser innerhalb der Toleranzzone liegen.
Beispiel 2
Die Achse des Merkmals D muss zwischen zwei parallelen Ebenen liegen, die in einem 45-Grad-Winkel zur Bezugsachse und in einem Abstand von 0,1 mm von ihr innerhalb der Toleranzzone liegen.
Konzentrizität ist der Zustand, bei dem die Achse, die am Teil gemessen wird, mit der Bezugsachse entlang derselben geraden Linie ausgerichtet bleibt.
Die Toleranzzone ist die Fläche innerhalb eines Zylinders, die einen Durchmesser des Toleranzwertes t hat und koaxial zur Bezugsachse liegt.
Beispiel 1
Die Achse des Merkmals D muss sich innerhalb eines Zylinders befinden, der einen Durchmesser von 0,1 mm hat und koaxial mit der Bezugsachse D innerhalb der Toleranzzone liegt.
Symmetrie ist der Zustand, bei dem zwei Paare symmetrischer Merkmale auf dem Teil in derselben Ebene ausgerichtet sind.
Die Toleranzzone ist die Fläche zwischen zwei parallelen Ebenen (oder Linien), die im Abstand des Toleranzwertes t von der Bezugsmittelebene (oder Mittellinie oder Achse) liegen und symmetrisch zu dieser angeordnet sind.
Werden zwei zueinander senkrechte Richtungen angegeben, so ist die Toleranzzone der Bereich innerhalb eines vierseitigen Prismas, dessen Querschnitt den Toleranzwerten t1 x t2 entspricht.
Beispiel 1
Die Mittelebene der Nut muss zwischen zwei parallelen Ebenen liegen, die symmetrisch zur Bezugsmittelebene und in einem Abstand von 0,1 mm von ihr innerhalb des Toleranzfeldes angeordnet sind.
Beispiel:
(1) Die Mitte der Klemme muss gerade ausgerichtet werden.
(2) Die maximale Abweichung einer Seite von der Mitte des Schlitzes darf 0,035 mm nicht überschreiten.
Frage?
(1) Wie wird der Offset T berechnet?
T=(b-a)/2
(2) Wie hoch ist die Symmetrietoleranz?
Die Positionstoleranz bezieht sich auf die Genauigkeit von Punkten, Linien, Flächen und anderen Elementen auf einem Teil im Verhältnis zu ihrer idealen Position.
Toleranzbereich:
(1) Lagetoleranz des Punktes: Die Toleranzzone ist die Fläche innerhalb eines Kreises oder einer Kugel mit dem Durchmesser des Toleranzwertes t, zentriert auf die ideale Lage des Punktes.
(2) Lagetoleranz der Linie: Bei Angabe einer Richtung ist die Toleranzzone die Fläche zwischen zwei parallelen Ebenen (oder Linien), die symmetrisch um die ideale Lage der Linie und im Abstand des Toleranzwertes t angeordnet sind. Sind zwei senkrechte Richtungen angegeben, ist die Toleranzzone die Fläche innerhalb eines vierseitigen Prismas mit der Querschnittsgröße t1 X t2, dessen Achsenlinie mit der idealen Lage der Linie zusammenfällt.
(3) Lagetoleranz der Oberfläche: Die Toleranzzone ist die Fläche zwischen zwei parallelen Ebenen, die symmetrisch um die ideale Lage der Oberfläche und in einem Abstand des Toleranzwertes t angeordnet sind.
Beispiel 1
Der Punkt muss sich innerhalb eines Kreises mit einem Durchmesser von 0,3 mm befinden, und der Mittelpunkt des Kreises liegt in der idealen Position der durch die relativen Bezugspunkte A und B bestimmten Punkte.
System mit drei Bezugsebenen:
Drei zueinander rechtwinklige Bezugsebenen A, B und C bilden ein Bezugsebenensystem, das gemeinhin als Drei-Bezugsebenen-System bezeichnet wird. Es ist der Ausgangspunkt für die Bestimmung der geometrischen Beziehungen der verschiedenen Elemente auf den Teilen.
Im System der drei Bezugsebenen sind die Bezugsebenen nach ihren Funktionen geordnet.
Die wichtigste ist die erste Bezugsebene (A), gefolgt von der zweiten (B) und dritten (C) Bezugsebene.
Beispiel 2
Die Achse der Bohrung muss sich innerhalb einer Zylinderfläche mit einem Durchmesser von 0,1 mm befinden, und die Achsenlinie der Zylinderfläche sollte mit der idealen Position der Punkte auf den relativen Bezugspunkten A, B und C übereinstimmen.
Beispiel 3
Zusammengesetzte Positionstoleranz.
Geometrischer Rahmen:
Es handelt sich um eine Grafik, die die korrekte geometrische Beziehung zwischen einer Reihe von idealen Achsenlinien oder zwischen diesen und dem Bezugspunkt zeigt.
Die Achse der vier D-Löcher muss sich innerhalb des Überlappungsbereichs zweier zylindrischer Toleranzfelder befinden, von denen das eine einen Durchmessertoleranzwert von 0,1 mm und das andere einen Durchmessertoleranzwert von 0,05 mm aufweist. Der geometrische Rahmen der vier 0,1-mm-Positionstoleranzfelder ist in Bezug auf die Bezugspunkte A, B und C festgelegt. Der geometrische Rahmen der vier 0,05-mm-Positionstoleranzfelder ist nur in Bezug auf den Bezugspunkt A ausgerichtet.
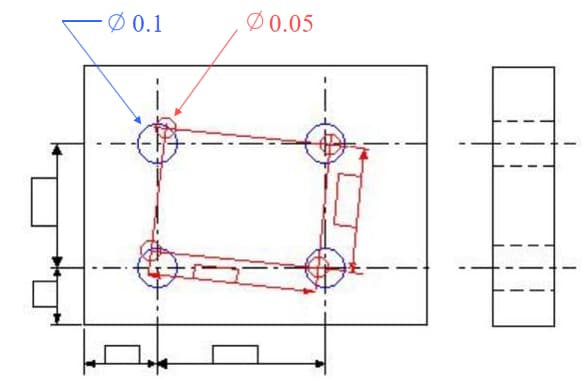
Die Achsen der vier D-Löcher müssen sich innerhalb des Überschneidungsbereichs zweier zylindrischer Toleranzfelder befinden, von denen eines einen Durchmessertoleranzwert von 0,1 mm und das andere einen Durchmessertoleranzwert von 0,05 mm hat. Der geometrische Rahmen der vier 0,1-mm-Positionstoleranzfelder ist in Bezug auf die Bezugspunkte A, B und C festgelegt. Der geometrische Rahmen der vier 0,05-mm-Positionstoleranzfelder ist nur in Bezug auf den Bezugspunkt A ausgerichtet.
Überlegung: Vergleich der beiden folgenden Arten der Positionsgenauigkeit.
Bezieht sich auf den Zustand, bei dem die rotierende Oberfläche auf dem Teil innerhalb der Messfläche begrenzt ist und ihre festgelegte Position relativ zur Bezugsachse beibehält.
(1) Radialer Rundlauf.
Die Toleranzzone ist die Fläche zwischen zwei konzentrischen Kreisen, deren Mittelpunkte auf der Bezugsachse liegen, wobei die Radiusdifferenz in einer beliebigen Messebene senkrecht zur Bezugsachse der Toleranzwert t ist.
(2) Rundlauf der Stirnseite.
Die Toleranzzone ist die zylindrische Fläche entlang der Mantellinie mit der Breite t auf dem Messzylinder an einer beliebigen, zur Bezugsachse koaxialen Durchmesserposition.
Beispiel 1
Radialer Rundlauf.
Wenn sich die zylindrische Fläche ohne axiale Bewegung um die Bezugsachse dreht, darf der Rundlauf in jeder Messebene den Toleranzwert von 0,05 mm nicht überschreiten.
Die Toleranzzone ist die Fläche zwischen zwei konzentrischen Kreisen, deren Mittelpunkte auf der Bezugsachse liegen, wobei die Radiusdifferenz in einer beliebigen Messebene senkrecht zur Bezugsachse der Toleranzwert t ist.
Beispiel 2
Rundlauf der Stirnseite.
Wenn sich das Teil um die Bezugsachse dreht, ohne dass eine axiale Bewegung stattfindet, darf der Planlauf an einem beliebigen Messdurchmesser an der linken Stirnseite den Toleranzwert von 0,05 mm nicht überschreiten.
Die Toleranzzone ist die zylindrische Fläche entlang der Mantellinie mit der Breite t auf dem Messzylinder an einer beliebigen, zur Bezugsachse koaxialen Durchmesserposition.
Bezieht sich auf den gleichmäßigen Rundlauf entlang der gesamten gemessenen Oberfläche des Teils, wenn es sich kontinuierlich um die Bezugsachse dreht.
(1) Radialer Gesamtrundlauf.
Die Toleranzzone ist die Fläche zwischen zwei zur Bezugsachse koaxialen Zylindern mit einer Radiusdifferenz des Toleranzwertes t
(2) Gesamtrundlauf der Stirnseite.
Die Toleranzzone ist die Fläche zwischen zwei parallelen Ebenen, die senkrecht zur Bezugsachse liegen und einen Abstand vom Toleranzwert t haben.
Beispiel 1
Radialer Gesamtrundlauf.
Wenn sich die Oberfläche kontinuierlich um die Bezugsachse dreht, ohne dass eine axiale Bewegung stattfindet, während sich der Indikator linear parallel zur Bezugsachse bewegt, darf der Rundlauf über die gesamte Oberfläche den Toleranzwert von 0,02 mm nicht überschreiten.
Die Toleranzzone ist die Fläche zwischen zwei zur Bezugsachse koaxialen Zylindern mit einer Radiusdifferenz des Toleranzwertes t.
Beispiel 2
Gesamtrundlauf der Stirnseite.
Wenn sich die Stirnfläche kontinuierlich um die Bezugsachse dreht, ohne dass eine axiale Bewegung stattfindet, während sich der Anzeiger linear und senkrecht zur Bezugsachse bewegt, darf der Rundlauf entlang der gesamten Stirnfläche den Toleranzwert von 0,05 mm nicht überschreiten.
Die Toleranzzone ist die Fläche zwischen zwei parallelen Ebenen, die senkrecht zur Bezugsachse liegen und einen Abstand vom Toleranzwert t haben.
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
AR 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO