Haben Sie sich jemals gefragt, wie Blechkonstrukteure die Genauigkeit ihrer Entwürfe sicherstellen? In diesem Blogbeitrag tauchen wir in die faszinierende Welt der Blechkonstruktion ein und erkunden zwei wesentliche Konzepte: Biegezugabe und Biegeabzug. Außerdem werden wir den K-Faktor und seine Rolle bei Berechnungen vorstellen. Seien Sie dabei, wenn wir diese Themen entschlüsseln und wertvolle Einblicke von Branchenexperten geben.
Im Bereich der Blechkonstruktion sind Begriffe wie Biegezugabe, Biegeabzug und K-Faktor entscheidende Begriffe, die sich erheblich auf die Genauigkeit und Effizienz von Fertigungsprozessen auswirken. Diese Parameter spielen eine entscheidende Rolle bei der Bestimmung der endgültigen Abmessungen von gebogenen Blechteilen und gewährleisten eine präzise Fertigung. Lassen Sie uns diese Begriffe näher betrachten und ihre Berechnungsmethoden erforschen.
Ingenieure und Hersteller, die mit der Blechbearbeitung befasst sind, verwenden hochentwickelte Algorithmen, um die Abmessungen der flachen Muster von Teilen genau zu berechnen und so eine präzise Endgeometrie nach den Biege- und Umformvorgängen zu gewährleisten.
Die traditionelle "Pinch-Methode" ist nach wie vor ein weit verbreiteter empirischer Ansatz, bei dem Faktoren wie Materialeigenschaften, Biegeradius, Biegewinkel, Werkzeugkonfigurationen und Umformgeschwindigkeiten berücksichtigt werden. Diese Methode ist zwar effektiv, hängt aber stark von der Erfahrung des Bedieners ab und kann zu Unstimmigkeiten führen.
Mit dem Aufkommen fortschrittlicher Berechnungswerkzeuge haben die computergestützte Konstruktion (CAD) und die Finite-Elemente-Analyse (FEA) die Genauigkeit und Effizienz der Blechkonstruktion revolutioniert. Diese Technologien ermöglichen eine präzise Simulation des Materialverhaltens während des Umformprozesses und berücksichtigen komplexe Phänomene wie Rückfederung, Eigenspannungen und Kaltverfestigung.
Moderne CAD-Systeme verwenden fortschrittliche Algorithmen zur Biegekompensation, die theoretische Modelle mit empirischen Daten verbinden. Diese Algorithmen verwenden in der Regel einen von zwei Hauptansätzen:
Führende CAD-Plattformen wie SolidWorks, Autodesk Inventor und Siemens NX bieten robuste Blechkonstruktionsmodule mit anpassbaren Biegetabellen und Materialbibliotheken. Diese Systeme ermöglichen die Integration werkstattspezifischer Biegedaten und gewährleisten so den Abgleich zwischen digitalen Konstruktionen und tatsächlichen Fertigungsprozessen.
Darüber hinaus werden neue Technologien wie maschinelles Lernen und künstliche Intelligenz eingesetzt, um Biegeberechnungen zu optimieren. Dabei werden umfangreiche Datensätze mit historischen Produktionsdaten genutzt, um Vorhersagen zu verfeinern und an einzigartige Material- und Werkzeugkombinationen anzupassen.
Verbesserung des Verständnisses der Leser für grundlegende Konzepte in Blechdesign Berechnung werden die folgenden Punkte zusammengefasst und erläutert:
Für ein besseres Verständnis der BiegezugabeSiehe Abbildung 1, die eine einzelne Biegung in einem Blechteil zeigt. Abbildung 2 zeigt das Bauteil in ungefaltetem Zustand.
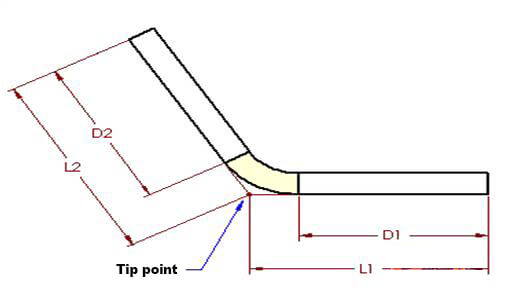
Abbildung 1
Abbildung 2
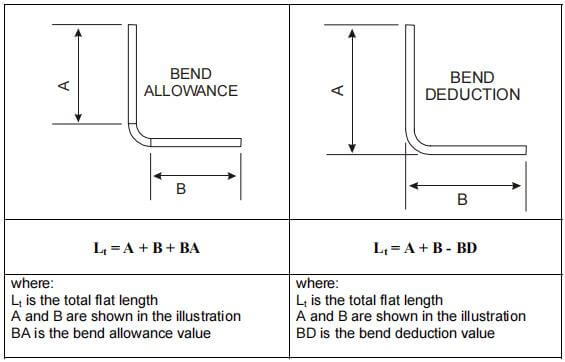
Der Algorithmus für Biegezugaben beschreibt die ungefaltete Länge (LT) eines Blechteils als die Summe der Längen der einzelnen Segmente nach dem Abflachen des Teils plus die Länge des abgeflachten Biegebereichs.
Die Biegezugabe (BA) steht für die Länge des abgeflachten Biegebereichs. Die Gesamtlänge des Teils kann also mit Gleichung (1) ausgedrückt werden:
LT = D1 + D2 + BA (1)
Der Biegebereich (in der Abbildung hellgelb dargestellt) ist der Bereich, der sich theoretisch während des Biegevorgangs verformt.
Um die Geometrie des abgewickelten Teils zu bestimmen, gehen Sie folgendermaßen vor:
Die Bestimmung der Länge des abgeflachten Biegebereichs, in der Abbildung durch BA dargestellt, ist etwas schwieriger.
Der Wert von BA variiert in Abhängigkeit von Faktoren wie Materialart und Materialstärke, Biegeradius und Winkel, sowie das Biegeverfahren, der Maschinentyp und die Maschinengeschwindigkeit.
Der Wert von BA kann aus verschiedenen Quellen entnommen werden, z. B. von Lieferanten von Blechwerkstoffen, experimentellen Daten, Erfahrungswerten und technischen Handbüchern.
In SolidWorks kann man BA-Werte direkt eingeben oder den K-Faktor (auf den später eingegangen wird) zur Berechnung der Werte verwenden.
Die Biegetisch Methode ist der genaueste Weg, um unterschiedliche Biegezugaben für verschiedene Situationen mit unterschiedlichen Dicken, Radien und Winkeln festzulegen.
Die Erstellung des ersten Biegetisches kann einige Zeit in Anspruch nehmen, aber wenn er einmal geformt ist, können Teile davon in Zukunft wiederverwendet werden.
Für jede Biegung des Teils können die gleichen oder unterschiedliche Informationen eingegeben werden.
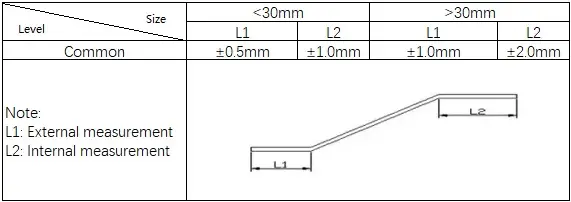
1) Normen für gemeinsames Biegen
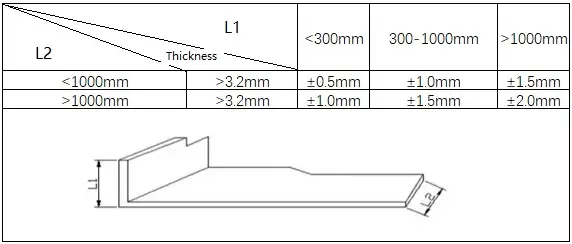
2) Normen für Z-Biegen
3) Normen für V-Biegen
4) Normen für U-Biegen
Weiterführende Lektüre: Rechner für V- und U-förmige Biegekräfte
Biegeabzug ist ein Begriff, der die Höhe des Rückschlags beim Prozess der Blechbiegen. Dies ist ein weiterer einfacher Algorithmus zur Beschreibung des Prozesses.
Die Abbildungen 1 und 2 gelten auch für dieses Konzept. Nach der Methode des Biegeabzugs ist die abgeflachte Länge (LT) des Teils gleich der Summe der Längen der beiden flachen Abschnitte bis zum "Spitzenpunkt" (dem hypothetischen Schnittpunkt der beiden flachen Abschnitte), abzüglich des Biegeabzugs (BD).
Die Gesamtlänge des Teils kann also wie in Gleichung (2) dargestellt ausgedrückt werden:
LT = L1 + L2 - BD (2)
Der Wert von BD kann aus verschiedenen Quellen ermittelt oder bezogen werden, z. B. aus Blättern Metallmaterial Lieferanten, experimentelle Daten, Erfahrungen, technische Handbücher mit Gleichungen oder Tabellen usw.
Abbildung 3
Für Anwender, die mit der Methode der Biegeabzüge vertraut sind, ist es wichtig, die Beziehung zur Methode der Biegezugabe zu verstehen, die üblicherweise in SolidWorks verwendet wird.
Die Beziehung zwischen den beiden Werten lässt sich leicht anhand der beiden Geometrien des Biegens und Entfaltens von Teilen ableiten.
Vergleicht man die Gleichungen (1) und (2), so ergibt sich Folgendes:
LT = D1 + D2 + BA (1) LT = L1 + L2 - BD (2)
Und deshalb,
D1 + D2 + BA = L1 + L2 - BD (3)
In Abbildung 3 stellt der Winkel A die Biegewinkeldie den Winkel beschreibt, den das Teil während des Biegens einnimmt, sowie den Winkel des Bogens, den die Biegefläche bildet, die in zwei Hälften dargestellt wird.
Mit Hilfe der Dimensionen und Prinzipien des rechtwinkligen Dreiecks können wir die folgenden Gleichungen ableiten:
D1 = L1 - (R + T)TAN(A/2) (4) D2 = L2 - (R + T)TAN(A/2) (5)
Wenn man die Gleichungen (4) und (5) in Gleichung (3) einsetzt, erhält man die Beziehung zwischen BA und BD:
BA = 2(R + T)TAN(A/2) - BD (6)
Und wenn der Biegewinkel 90 Grad beträgt, vereinfacht sich diese Gleichung zu:
BA = 2(R + T) - BD (7)
Diese Gleichungen (6) und (7) bieten eine bequeme Methode für die Umrechnung von einem Algorithmus in den anderen, wobei nur die Materialstärke, der Biegewinkel/-radius usw. als Parameter verwendet werden.
Für SolidWorks-Anwender bieten diese Gleichungen eine direkte Methode zur Umwandlung von Biegeabzug in Biegezugabe.
Der Wert für die Biegezugabe kann für das gesamte Teil oder für jede einzelne Biegung verwendet werden, oder er kann in eine Biegedatentabelle aufgenommen werden.
Der K-Faktor ist ein eigenständiger Wert, der das Biegen und Entfalten von Blechen in verschiedenen geometrischen Szenarien erklärt.
Es handelt sich auch um einen autonomen Wert, der zur Berechnung der Biegezugabe (BA) unter verschiedenen Bedingungen wie unterschiedlichen Materialstärken, Biegewinkeln und Radien verwendet wird.
Die Abbildungen 4 und 5 dienen der Verdeutlichung der ausführlichen Definition des K-Faktors.
Abbildung 4
Abbildung 5
Wir können bestätigen, dass es eine neutrale Achse in der Dicke des Blechteils gibt. Das Blech Metallmaterial in dieser neutralen Achse im Biegebereich weder gestreckt noch gestaucht wird, d. h. es ist der einzige Bereich, der sich beim Biegen nicht verformt.
Die Abbildungen 4 und 5 zeigen die Grenze zwischen den rosa und blauen Regionen.
Während des Biegens wird der rosa Bereich zusammengedrückt und der blaue Bereich gestreckt. Wenn die neutrale Blechschicht unverformt bleibt, bleibt die Länge ihres Bogens im Biegebereich gleich, egal ob das Teil gebogen oder abgeflacht wird.
Folglich sollte die Biegezugabe (BA) der Länge des Bogens der neutralen Schicht im Biegebereich des Blechteils entsprechen, was in Abbildung 4 grün dargestellt ist.
Die Lage der neutralen Schicht eines Blechs hängt von den Eigenschaften eines bestimmten Materials ab, z. B. von der Duktilität.
Es wird davon ausgegangen, dass der Abstand zwischen der neutralen Blechlage und der Oberfläche "t" beträgt, also die Tiefe von der Oberfläche des Blechteils in das Material in Dickenrichtung.
Folglich kann der Radius des Bogens der neutralen Schicht als (R + t) ausgedrückt werden. Mit diesem Ausdruck und dem Biegewinkel kann die Länge des Bogens der neutralen Schicht (BA) berechnet werden.
BA = Pi(R+T)A/180
Um die Definition der blechneutralen Schicht zu vereinfachen und für alle Materialien anwendbar zu machen, wurde das Konzept des K-Faktors eingeführt.
Die Definition des K-Faktors lautet: Er ist das Verhältnis zwischen der Dicke der neutralen Schicht des Blechs und der Gesamtdicke des Materials des Blechteils. Mit anderen Worten, der K-Faktor ist definiert als:
K = t/T
Daher wird der Wert von K immer im Bereich von 0 bis 1 liegen. Ein K-Faktor von 0,25 bedeutet, dass die neutrale Schicht bei 25% der Gesamtdicke des Blechmaterials liegt.
Wenn er 0,5 beträgt, bedeutet dies, dass sich die neutrale Schicht auf 50% der gesamten Dicke befindet, usw.
Kombiniert man die oben genannten Gleichungen, erhält man die folgende Gleichung (8):
BA = Pi(R+K*T)A/180 (8)
Daher wird der Wert von K immer zwischen 0 und 1 liegen.
Wenn der K-Faktor 0,25 beträgt, bedeutet dies, dass die neutrale Schicht bei 25% der Dicke des Blechmaterials des Teils liegt.
Wenn der Wert 0,5 beträgt, bedeutet dies, dass sich die neutrale Schicht auf 50% der gesamten Dicke befindet usw.
Der Ursprung des K-Faktors lässt sich auf traditionelle Quellen wie Lieferanten von Blechwerkstoffen, Testdaten, Erfahrungen, Handbücher usw. zurückführen.
In einigen Fällen lässt sich der angegebene Wert jedoch nicht als eindeutiger K-Faktor ausdrücken, aber es ist dennoch möglich, die Beziehung zwischen ihnen zu ermitteln.
Wenn beispielsweise in einem Handbuch oder in der Literatur beschrieben wird, dass die neutrale Achse in einem Abstand von 0,445x Materialdicke von der Blechoberfläche positioniert ist, kann dies als ein K-Faktor von 0,445 interpretiert werden, was k = 0,445 bedeutet.
Setzt man diesen Wert von K in Gleichung (8) ein, erhält man die folgende Formel
BA = A (0,01745R + 0,00778T)
Wenn Gleichung (8) durch eine andere Methode modifiziert wird, die Konstante in Gleichung (8) berechnet wird und alle Variablen beibehalten werden, ergibt sich Folgendes:
BA = A (0,01745 R + 0,01745 K*T)
Vergleicht man die beiden Gleichungen, so lässt sich leicht feststellen, dass 0,01745 * k = 0,00778 ist, so dass sich k auf 0,445 berechnen lässt.
Es hat sich herausgestellt, dass das SolidWorks-System auch einen Algorithmus für Biegezugaben für bestimmte Materialien bereitstellt, wenn der Biegewinkel 90 Grad beträgt. Die Berechnungsformel für jedes Material lautet wie folgt:
Wenn man die Gleichung (7) vereinfacht und den Biegewinkel auf 90 Grad setzt, kann man die Konstante berechnen und die Gleichung wie folgt umformen:
BA = (1,57 * K * T) + (1,57 *R)
Durch Vergleich der obigen Berechnungsformel kann der Wert von K für weiche Messing- oder Kupferwerkstoffe daher als 1,57xk = 0,55 oder K = 0,35 ermittelt werden.
Mit der gleichen Methode lassen sich die K-Faktor-Werte für die verschiedenen oben genannten Materialtypen leicht berechnen.
Wie bereits erwähnt, gibt es mehrere Quellen, aus denen der Wert des K-Faktors entnommen werden kann, z. B. Materiallieferanten, Testdaten, Erfahrungswerte und Handbücher.
Um ein genaues Blechmodell mit der K-Faktor-Methode zu erstellen, ist es entscheidend, die geeignete Quelle für den K-Faktor zu finden, die Ihren technischen Anforderungen entspricht. So wird sichergestellt, dass die Ergebnisse des physischen Teils so genau wie gewünscht sind.
In manchen Situationen ist es nicht möglich, mit einem einzigen K-Faktor-Wert allein genaue Ergebnisse zu erzielen, vor allem, wenn ein breites Spektrum von Biegeszenarien berücksichtigt werden muss.
In solchen Fällen ist es ratsam, den Wert der Biegezugabe (BA) direkt für eine einzelne Biegung des gesamten Teils zu verwenden oder eine Biegetabelle zu benutzen, um die verschiedenen BA-, Biegeabzugs- oder K-Faktor-Werte zu beschreiben, die verschiedenen A-, R- und T-Werten über den gesamten Bereich entsprechen.
Außerdem können Gleichungen verwendet werden, um Daten wie die von SolidWorks bereitgestellte Beispiel-Biegetabelle zu erzeugen. Falls erforderlich, können die Zellen in der Biegetabelle auch auf der Grundlage experimenteller oder empirischer Daten geändert werden.
Das Installationsverzeichnis von SolidWorks enthält Tabellen mit Biegezugaben, Biegeabzügen und K-Faktoren, die nach Bedarf bearbeitet und angepasst werden können.
Dieser Beitrag gibt einen umfassenden Überblick über die gängigen Berechnungsmethoden und die ihnen zugrunde liegenden Prinzipien, die bei der Konstruktion und Fertigung von Blechteilen verwendet werden.
Er behandelt die Berechnung von Biegezugaben, Biegeabzügen und K-Faktoren und erklärt die Unterschiede zwischen diesen Methoden und ihre Zusammenhänge.
Es dient als nützliches Nachschlagewerk für Ingenieure und technische Fachkräfte in der Branche.
Anmerkung:
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
AR 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO