Eigenfrequenz vs. Resonanzfrequenz: Der Unterschied wird erklärt

In der täglichen Analyse verwechseln wir oft Eigenfrequenz und Resonanzfrequenz und denken, dass sie dasselbe sind.

Dies ist in der Tat nicht rigoros.

Die Eigenfrequenz ist die Leistung der natürlichen Eigenschaften der Struktur, während die Resonanzfrequenz die Leistung der Reaktion der Struktur auf äußere Kräfte ist.

Freie Schwingung eines Federsystems mit einem Freiheitsgrad

Ein System mit einem einzigen Freiheitsgrad ist ein System, bei dem die Position zu einem bestimmten Zeitpunkt vollständig durch nur eine verallgemeinerte Koordinate bestimmt werden kann. Einfacher ausgedrückt: Die Kraft, die auf einen Körper einwirkt, wirkt nur in eine Richtung. Die Bewegung der Puppe in der folgenden Abbildung kann als Feder-Masse-System dargestellt werden.

Ein vereinfachtes Modell des Feder-Masse-Systems kann in der folgenden Abbildung dargestellt werden.

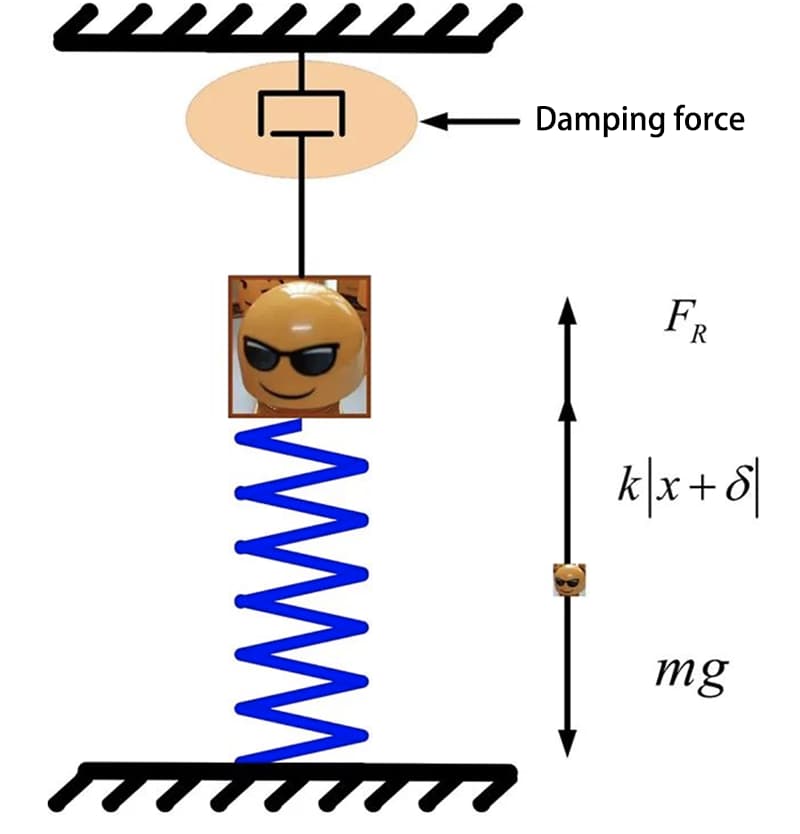
Die statische Gleichgewichtsposition des Tonabnehmerblocks gilt als Koordinatenursprung und wird als positiv betrachtet, wenn er sich entlang der Richtung der Federverformung vertikal nach unten bewegt. Der Abstand zwischen dem Block und der Gleichgewichtsposition kann als x dargestellt werden, und die Differentialgleichung der Bewegung für den Block kann wie folgt ausgedrückt werden:

Dabei ist m die Masse des Blocks, k die Federsteifigkeit, c der Viskositätskoeffizient, 2n=c/m der Dämpfungskoeffizient, und wenn der Dämpfungskoeffizient Null ist, entspricht er dem ungedämpften Schwingungssystem.

Eigenfrequenz Pn:

Die Eigenfrequenz ist nur von der Masse und der Steifigkeit abhängig und wird von Faktoren wie der Dämpfung nicht beeinflusst. Strukturelle Randverbindungen, MaterialeigenschaftenForm und andere Faktoren können sich auf die Eigenfrequenz auswirken, aber diese Einflüsse spiegeln sich in der Steifigkeit und der Masse wider und sind nicht die letztlich entscheidenden Faktoren.

Erzwungene Schwingung eines Federsystems bei harmonischer Erregung

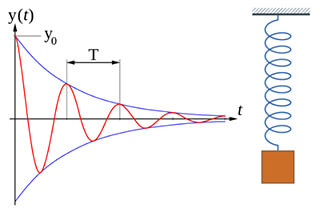
Die freie Schwingung ist die Schwingung des Systems ohne äußere Anregung, und die Bewegungsspur hängt mit dem Ausgangszustand und den natürlichen Eigenschaften zusammen.

Die erzwungene Schwingung bezieht sich auf die Schwingung, die das System bei externer Anregung erzeugt.

Die äußere Anregung ist im Allgemeinen eine periodische oder aperiodische Funktion der Zeit, von denen die einfache harmonische Anregung die einfachste ist.

Die einfache harmonische Erregungskraft sei:

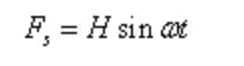
Dabei ist H die Amplitude der anregenden Kraft und ω die Winkelfrequenz der anregenden Kraft.

Wenn der Klotz um eine Strecke von x von der Gleichgewichtslage abweicht, lautet die Differentialgleichung der Bewegung des Klotzes

Mit h=H/m ist die obige Gleichung die Differentialgleichung der erzwungenen Schwingung eines einzelnen Freiheitsgrades mit viskoser Dämpfung, die eine lineare, inhomogene gewöhnliche Differentialgleichung mit konstantem Koeffizienten zweiter Ordnung ist.

Die obige Gleichung stimmt vollständig mit dem Ausdruck für die Spannungsantwort bei kapazitiver Last überein, den wir in der Schaltungstheorie kennen gelernt haben und der eine lineare, nicht homogene gewöhnliche Differentialgleichung mit konstantem Koeffizienten zweiter Ordnung ist.

Die Dämpfung im Stromkreis hängt vom Widerstand ab, denn der Widerstand verbraucht nur Energie und speichert sie nicht.

Bei einfacher harmonischer Erregung wird die Gesamtlösung der Differentialgleichung der Bewegung eines gedämpften Systems wie folgt festgelegt:

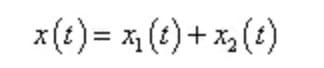
Dabei ist x1 (t) eine homogene Lösung, die eine freie, gedämpfte Schwingung darstellt;

Aufgrund der Dämpfung verschwindet der gedämpfte Schwingungsanteil nach einer gewissen Zeit.

Die Lösung ist dieselbe wie bei den freien Schwingungen, so dass sie hier nicht wiederholt werden muss.

Hier geht es um die spezielle Lösung x₂ (t), die durch erzwungene Schwingungen erzeugt wird, ausgedrückt werden kann als:

Darunter,

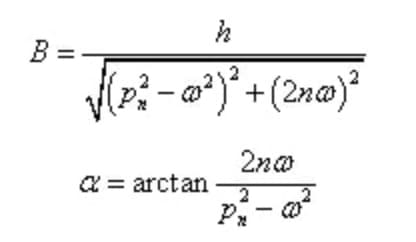
Amplitude und Phasenverschiebung der erzwungenen Dauerschwingung sind unabhängig von den Anfangsbedingungen, sondern hängen nur von den Eigenschaften des Systems und der Erregung ab.

Stellen Sie das Frequenzverhältnis, das Dämpfungsverhältnis und den Amplitudenverstärkungskoeffizienten wie folgt ein:

Die obige Formel kann wie folgt umgeschrieben werden:

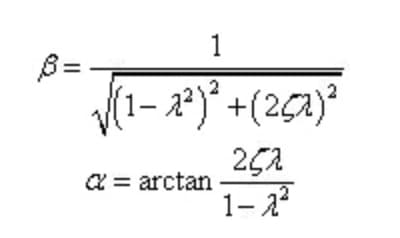
Auf dieser Grundlage können wir die Reaktion des Systems auf die erzwungene Schwingung ermitteln.

Zum besseren Verständnis kann die Beziehung zwischen verschiedenen Dämpfungsverhältnissen, Frequenzverhältnissen und Amplitudenverstärkungskoeffizienten dargestellt werden. Die Frequenz wird in drei Bereiche unterteilt: Niederfrequenz, Mittelfrequenz und Hochfrequenz. Wie in der Abbildung zu sehen ist, hat die Dämpfung sowohl im niederfrequenten als auch im hochfrequenten Bereich einen minimalen Einfluss auf den Amplitudenverstärkungskoeffizienten. Daher kann das gedämpfte System zur leichteren Berechnung als ungedämpftes System vereinfacht werden.

Eigenfrequenz und Resonanzfrequenz

Die Eigenfrequenz ist ein inhärentes Merkmal der strukturellen Eigenschaften eines Systems, das ausschließlich durch seine Masse und Steifigkeit bestimmt wird, unabhängig von äußeren Faktoren wie der Dämpfung. In einem System mit n Freiheitsgraden gibt es n verschiedene Eigenfrequenzen, während kontinuierliche Systeme eine unendliche Anzahl von Eigenfrequenzen besitzen.

Resonanz tritt auf, wenn eine äußere Anregungsfrequenz eng mit der Eigenfrequenz eines Systems übereinstimmt oder mit ihr zusammenfällt, so dass die Struktur mit deutlich erhöhter Amplitude schwingt. Dieses Phänomen wird in der nebenstehenden Abbildung durch den blauen Kreis dargestellt. Während die Resonanzfrequenz bei leicht gedämpften Systemen oft der Eigenfrequenz nahe kommt, kann sie bei stark gedämpften Strukturen von dieser abweichen und in der Regel niedriger als die Eigenfrequenz sein.

Bei der Systemauslegung ist es von entscheidender Bedeutung, nicht nur die spezifische Resonanzspitzenfrequenz zu vermeiden, sondern auch das umgebende Resonanzband, das dem Zwischenfrequenzbereich in der Abbildung entspricht. Diese Vorsichtsmaßnahme ist notwendig, weil die Reaktion des Systems innerhalb dieses Bandes erheblich verstärkt bleibt. Die Ingenieure müssen sicherstellen, dass weder der normale Betrieb des Systems noch externe Erregungen durch nahe gelegene Geräte in diesen kritischen Bereich fallen.

Resonanz kann tiefgreifende Auswirkungen haben, sowohl positive als auch negative. Zu den negativen Auswirkungen gehören der Einsturz von Hebebalken, Bodenresonanzen in Hubschraubern, Maschinenschäden und durch Infraschall verursachte Strukturschäden. Umgekehrt wird die Resonanz in Musikinstrumenten bewusst eingesetzt, um die gewünschten Töne und Obertöne zu erzeugen.

Um die mit der Resonanz verbundenen Risiken zu mindern, setzen die Designer verschiedene Strategien ein:

1. Frequenzabstimmung: Anpassung der Eigenfrequenz des Systems zur Vermeidung von Betriebsfrequenzbereichen.
2. Verstärkung der Dämpfung: Einsatz von Materialien oder Mechanismen zum Abbau von Schwingungsenergie.
3. Strukturelle Verstärkung: Erhöhung der Steifigkeit, um die Eigenfrequenzen zu verändern und die Amplituden zu verringern.
4. Schwingungsisolierung: Implementierung von Systemen zur Minimierung der Übertragung von externen Erregungen.
5. Aktive Steuerung: Einsatz von Sensoren und Aktoren, um Resonanzschwingungen in Echtzeit entgegenzuwirken.

Das Verständnis und die Beherrschung von Resonanz ist in Bereichen wie dem Bauwesen, der Luft- und Raumfahrt, der Präzisionsfertigung und dem Design von Musikinstrumenten unerlässlich. Fortschrittliche Analysewerkzeuge wie die Finite-Elemente-Analyse und die experimentelle Modalanalyse spielen eine entscheidende Rolle bei der Vorhersage und Charakterisierung des Resonanzverhaltens in komplexen Systemen.