Achtung an alle Metallbearbeitungsfans! Sind Sie es leid, die richtige Tonnage für Ihre Abkantpresse zu erraten? Dann suchen Sie nicht weiter! In diesem Blogbeitrag tauchen wir in die Welt der Tonnageberechnung für Abkantpressen ein, angeleitet von der Expertise eines erfahrenen Maschinenbauingenieurs. Entdecken Sie praktische Formeln, handliche Tabellen und Insider-Tipps, um die Kunst des präzisen und effizienten Biegens von Blechen zu meistern. Machen Sie sich bereit, Ihr Abkantpressen-Spiel zu verbessern!
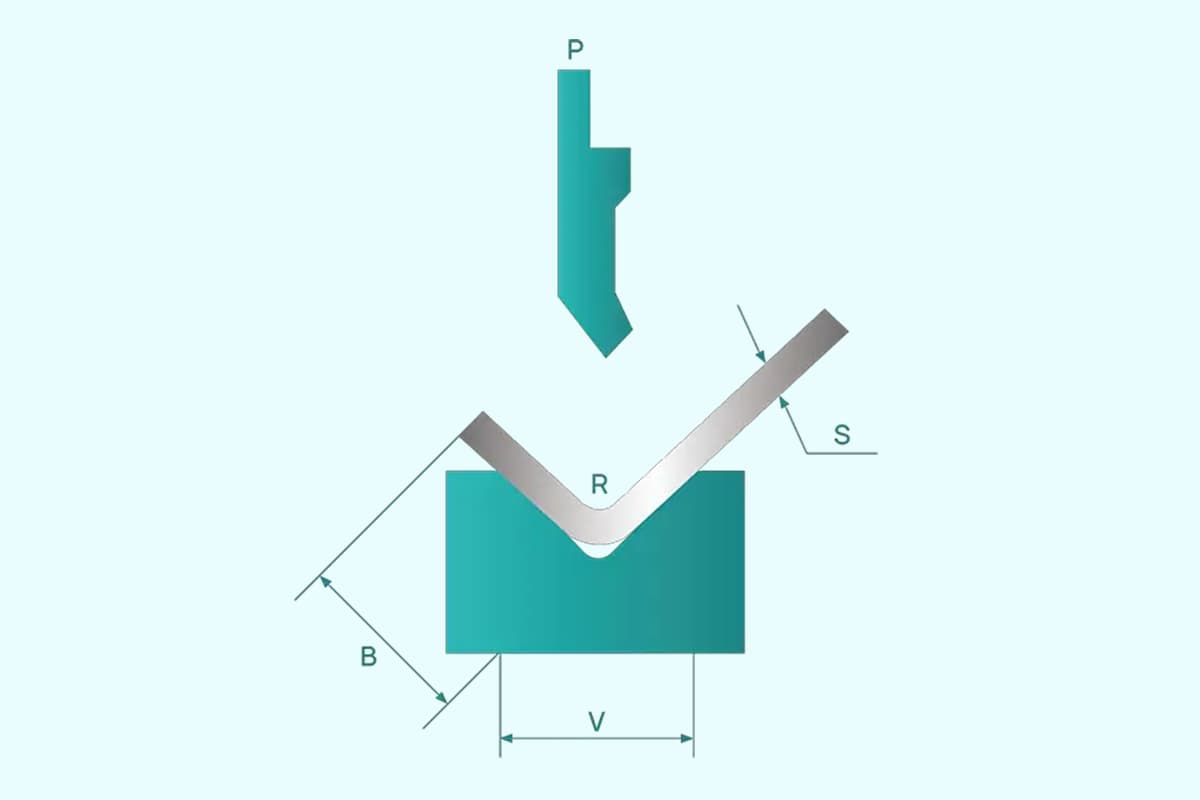
Die Tonnage einer Abkantpresse ist die Kraft, die zum Biegen einer Metallplatte mit einer Abkantpresse erforderlich ist. Diese in Tonnen gemessene Kraft ist für das Erreichen präziser Biegungen bei der Metallherstellung von entscheidender Bedeutung. Eine genaue Tonnageberechnung gewährleistet qualitativ hochwertige Ergebnisse und verlängert die Lebensdauer der Ausrüstung, indem sie Probleme wie Werkzeugschäden und ungenaue Biegungen verhindert.
Verschiedene Materialien erfordern aufgrund ihrer Zugfestigkeit unterschiedliche Kräfte. So benötigt beispielsweise Edelstahl im Vergleich zu Aluminium eine höhere Tonnage. Auch die Materialstärke wirkt sich erheblich auf die erforderliche Kraft aus, da dickere Materialien exponentiell mehr Kraft zum Biegen benötigen.
Die Länge der Biegung beeinflusst die benötigte Tonnage. Längere Biegungen erfordern mehr Tonnage aufgrund des erhöhten Widerstands entlang der Materiallänge.
Die Größe der Matrizenöffnung beeinflusst die erforderliche Kraft. Kleinere Matrizenöffnungen erfordern eine höhere Tonnage, da das Material in einen engeren Raum gepresst werden muss, während größere Matrizenöffnungen weniger Kraft erfordern.
Die Art des Werkzeugs, z. B. V-Stempel oder gekröpfte Werkzeuge, wirkt sich auf die Tonnageanforderungen aus. So müssen beispielsweise Schwanenhalswerkzeuge, die so konstruiert sind, dass sie das Werkstück nicht beeinträchtigen, vorsichtig gehandhabt werden, um eine zu hohe Tonnage zu vermeiden.
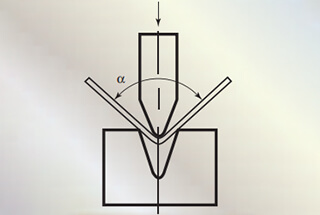
Die Biegemethode - Luftbiegen, Bodenbiegen oder Prägen - hat Auswirkungen auf die Tonnage. Das Luftbiegen erfordert die geringste Tonnage, das Bodenbiegen erfordert mehr und das Prägen die höchste Tonnage.
Sie können den folgenden Abkantpressen-Tonnage-Rechner verwenden, um die erforderliche Biegekraft für Ihre Blechbiegen. Der Rechner bietet sowohl metrische als auch imperiale Einheiten. Ich persönlich empfehle die Verwendung des unten stehenden Abkantpressen-Tonnage-Rechners, da dies wahrscheinlich die beste und bequemste Methode zur Berechnung der erforderlichen Biegekraft ist.
Die empfohlene V-Öffnungsbreite für das Unterwerkzeug
| S | 0,5-3 mm | 3-8mm | 9-10mm | >12mm |
| V | 6*S | 8*S | 10*S | 12*S |
Zum Beispiel, wenn die Feinblech Wenn es sich bei dem zu biegenden Material um Baustahl mit einer Dicke von 4 mm und einer Biegelänge von 3,2 m handelt, sollte die theoretische Breite der unteren Matrizenöffnung das Achtfache der Dicke betragen, also 32 mm. Geben Sie diese Zahlen in den obigen Rechner ein (beachten Sie, dass die Einheiten in mm angegeben sind), und Sie erhalten einen Wert von 106,12 Tonnen.
Das bedeutet, dass Sie eine Mindestbiegekraft von 106 Tonnen benötigen, um Ihre Biegeanforderungen zu erfüllen. Natürlich multiplizieren wir das Endergebnis im Allgemeinen mit einem Sicherheitsfaktor von 1,1, und der daraus resultierende Wert ist die Abkantpressentonnage, die Sie wählen können.
Wenn das Verhältnis von Breite zu Dicke (V/S) ungleich 9 und das Verhältnis von Radius zu Breite ungleich 0,16 ist, ist die obige Berechnung ungültig.
Bitte prüfen Sie die Aktualisierte Methode zur Berechnung der Biegekraft auf einer Abkantpresse.
Verwenden Sie stattdessen den folgenden Biegekraft-Rechner.
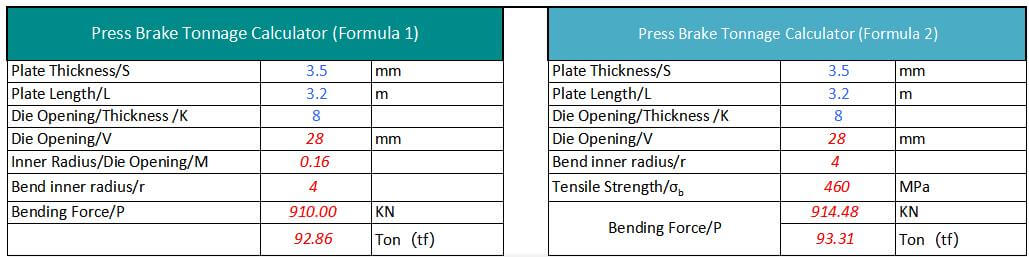
Die Größe der Biegekraft wird durch Faktoren wie die Größe des Werkstücks, die mechanischen Eigenschaften des Materials, den Abstand zwischen den Drehpunkten der Matrize, den relativen Biegeradius, den Abstand zwischen den Matrizen, den Reibungskoeffizienten zwischen dem Material und der Matrize, den Mindest Biegewinkelund die Biegemethode.
Daher ist es schwierig, die Biegekraft in der Theorie genau zu berechnen.
In der Praxis werden üblicherweise empirische Formeln oder vereinfachte theoretische Formeln zur Berechnung verwendet.
Derzeit gibt es zwei gängige Formeln für die Berechnung der Tonnage der Abkantpresse.
Die erste Formel wird üblicherweise in China verwendet, die zweite in anderen Ländern.
Unabhängig davon, welche Formel verwendet wird, ist der berechnete erforderliche Abkantpressdruck im Grunde derselbe. Im Folgenden möchte ich diese beiden Formeln getrennt voneinander vorstellen.
wo,
Zum Beispiel:
Plattenstärke S=4mm, Breite L=3m, σb=450N/mm²
Im Allgemeinen ist die Schlitzbreite V=S*8
Daher P=650*4²*3/4*8=975 (KN) = 99,5 (Tonne)
Das mit der Biegekraftformel ermittelte Ergebnis ist den Daten in der Biegekrafttabelle sehr ähnlich.
Beachten Sie, dass die Methode #1 zur Berechnung der Abkantpressentonnage auf milden Stahlwerkstoff.
Wenn es sich bei dem Material um Edelstahl, Aluminium oder Messing handelt, können Sie die Berechnungsergebnisse leicht anpassen, indem Sie sie mit den in der folgenden Tabelle aufgeführten Koeffizienten multiplizieren.
| Material | Koeffizienten |
| Baustahl | 1 |
| Rostfreier Stahl | 1.6 |
| Aluminium | 0.65 |
| Messing | 0.5 |
Zum Beispiel:
Plattenstärke S=4mm, Breite L=3m, σb=450N/mm²
Im Allgemeinen ist die Schlitzbreite V=S*8
Daher P=1,42*450*4²*3/48=958,5 (KN) = 96 (Tonne)
Der Schlüssel zum Biegeblech Metall mit verschiedenen Materialien ist die Zugfestigkeit des jeweiligen Materials zu bestimmen und dann die erforderliche Biegekraft mit Hilfe der oben genannten Formel zu berechnen.
Die nachstehende Zugfestigkeitstabelle kann als Referenz dienen:
| Material | Weich (N/mm²) | Hart (N/mm²) |
|---|---|---|
| Blei | 25 – 40 | – |
| Zinn | 40 – 50 | – |
| Aluminium | 93 | 1710 |
| Aluminiumlegierung Typ 4 | 230 | 480 |
| Duralumin | 260 | 480 |
| Zink | 150 | 250 |
| Kupfer | 220 – 280 | 300 – 400 |
| Messing (70:30) | 330 | 530 |
| Messing (60:40) | 380 | 490 |
| Phosphor Bronze / Bronze | 400 – 500 | 500 – 750 |
| Neusilber | 350 – 450 | 550 – 700 |
| Kaltgewalztes Eisen | 320 – 380 | – |
| Stahl .1% Kohlenstoff | 320 | 400 |
| Stahl .2% Kohlenstoff | 400 | 500 |
| Stahl .3% Kohlenstoff | 450 | 600 |
| Stahl .4% Kohlenstoff | 560 | 720 |
| Stahl .6% Kohlenstoff | 720 | 900 |
| Stahl .8% Kohlenstoff | 900 | 1100 |
| Stahl 1.0% Kohlenstoff | 1000 | 1300 |
| Siliziumstahl | 550 | 650 |
| Rostfreier Stahl | 650 – 700 | – |
| Nickel | 440 – 500 | 570 – 630 |
Beim Luftbiegen wird die Öffnungsweite V der Untergesenk wird in der Regel auf das 8- bis 10-fache der Blechdicke S festgelegt.
Hersteller von Abkantpressen führen die entsprechenden Werte der Matrizenbreite V und des Innendurchmessers r des zu biegenden Werkstücks häufig in ihrer Biegekraftparametertabelle auf.
Als allgemeine Regel gilt,
r=(0,16~0,17)V
Wenn der innere Radius jedoch nicht gleich (0,16-0,17)V ist, ist die obige Berechnungsformel nicht mehr anwendbar.
In diesen Fällen müssen Sie sich an einen neue Berechnungsmethode um die erforderliche Biegekraft oder Abkantpresskraft zu bestimmen.
Im Folgenden finden Sie den Rechner:
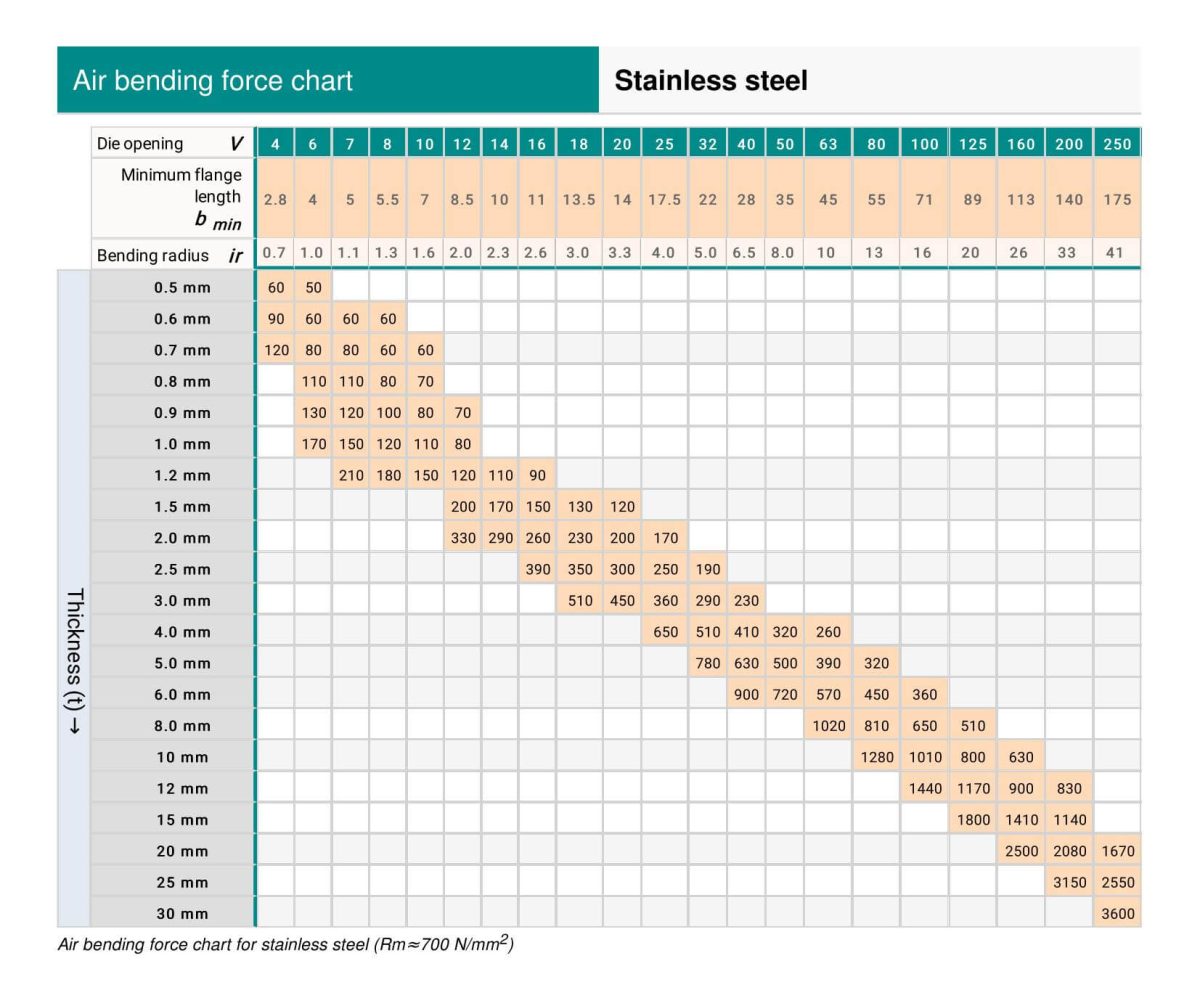
Die nachstehende Tabelle für die Abkantpressen-Tonnage kann Ihnen helfen, die erforderliche Biegekraft leicht zu bestimmen.
Anleitungen zum Lesen einer Tonnagentabelle für Abkantpressen finden Sie unter diese Stelle.
Siehe auch:
Daten von V, R, B
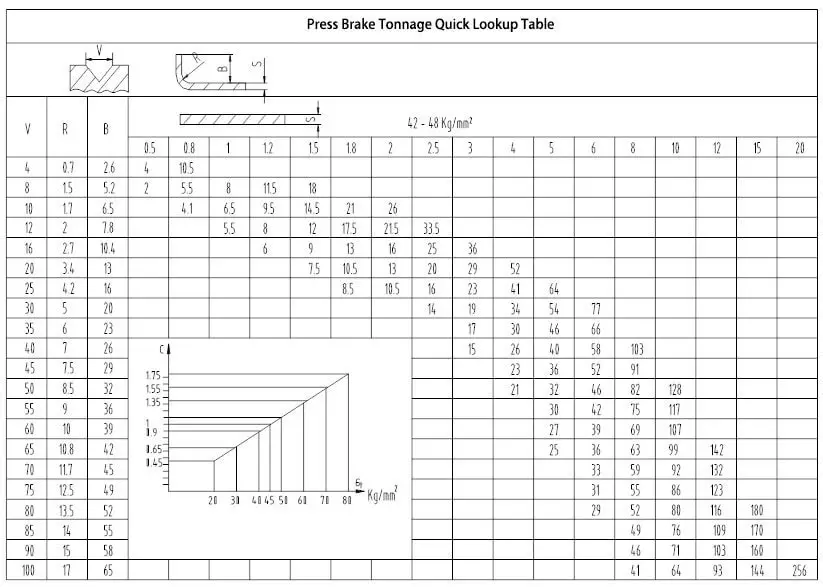
Wie liest man Tonnagetabellen für Abkantpressen?
Die in der Tonnentabelle der Abkantpresse angegebene Tonnage basiert auf einem Blech mit einer Zugfestigkeit von σb=450N/mm² und einer Länge von L=1m.
Jetzt, wo Sie die Biegung haben KräfteplanDer nächste Schritt besteht darin, zu verstehen, wie die Tonnage der Abkantpresse in der Tabelle zu finden ist.
Angenommen, Ihr Metallblech eine Dicke von 4 mm hat, gilt die allgemeine Regel, dass die V-Öffnung der Unterform das 8-fache der Blechdicke betragen sollte.
Bei dickeren Platten ist jedoch eine größere V-Öffnung erforderlich.
Die unten aufgeführten empfohlenen V-Öffnungen können als Anhaltspunkt dienen:
| S | 0,5-3 mm | 3-8mm | 9-10mm | >12mm |
| V | 6*S | 8*S | 10*S | 12*S |
Nehmen wir ein Metallblech mit einer Dicke von 4 mm.
In der Regel sollte die V-förmige Öffnung der Untermatrize das 8-fache der Blechdicke betragen. Bei dickeren Blechen sollte die V-förmige Öffnung jedoch größer sein.
Um die benötigte Abkantpressentonnage zu bestimmen, müssen wir die Abkantpressentonnentabelle heranziehen.
Suchen Sie zunächst die Reihe mit dem Dickenwert "4" und bestimmen Sie dann den entsprechenden Wert für die Öffnung der Vee von 32 (4 * 8).
Der Schnittpunkt der Zeile und der Spalte, in der sich die Werte "4" und "32" treffen, ergibt eine Tonnage von 330 KN.
Wenn wir ein 4 mm dickes Blech mit einer Länge von 3 m biegen müssen, beträgt die erforderliche Tonnage 330 * 3 = 990 KN, also etwa 101 Tonnen. In diesem Fall empfehlen wir, eine Abkantpresse mit einer Tonnage von mindestens 100 Tonnen zu wählen.
Es ist jedoch besser, sich für eine größere Tonnage, z. B. 120 Tonnen, zu entscheiden, da die Lebensdauer der Maschine länger ist, wenn sie über längere Zeit unter Volllast arbeitet.
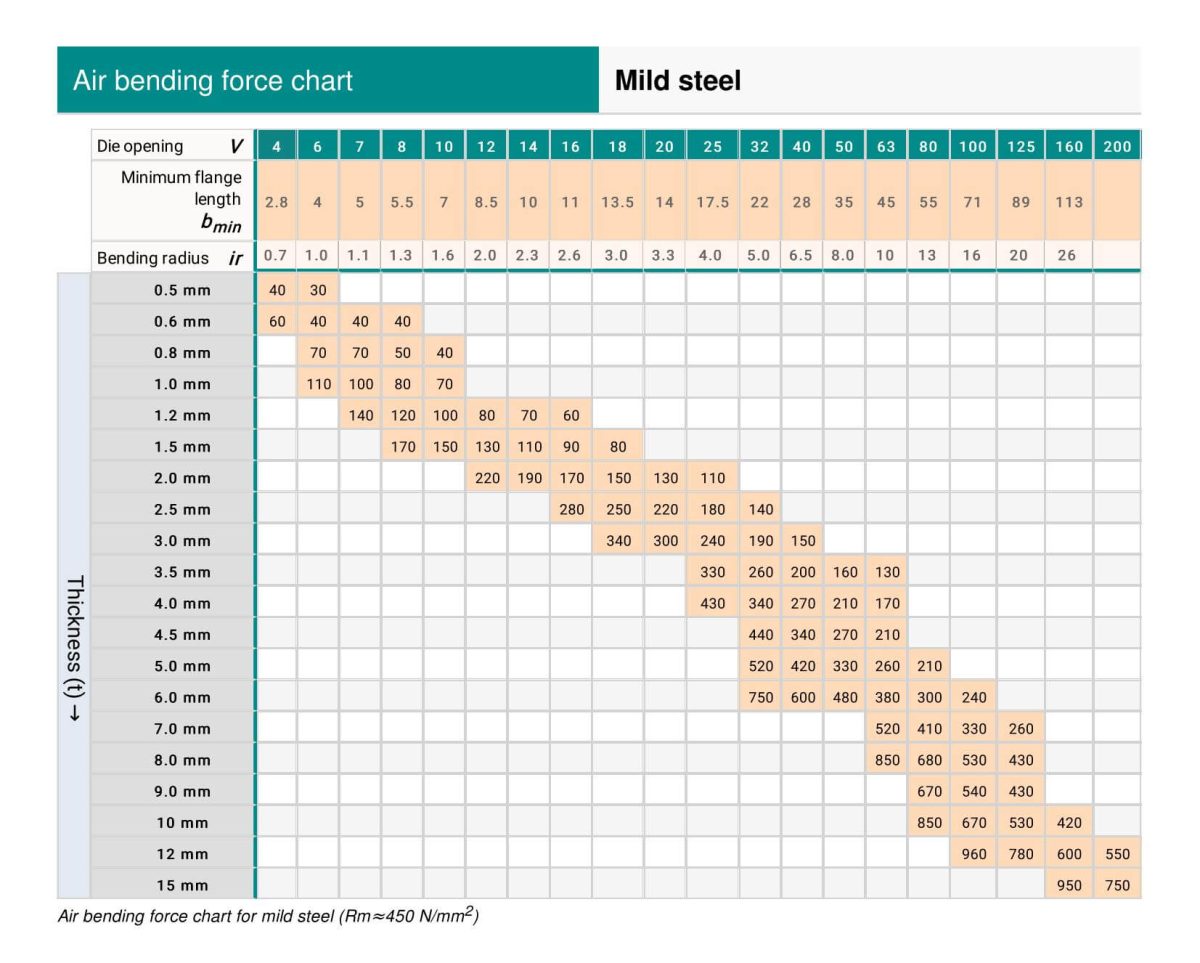
Säumen ist ein Art der Biegung die im Vergleich zum Standard-Luftbiegen eine höhere Tonnage erfordert.
Die folgenden Tabellen veranschaulichen die Tonnage, die für das Säumen und Falzen benötigt wird.
(1) Tonnentabelle für Säumen und Falzen von Baustahl
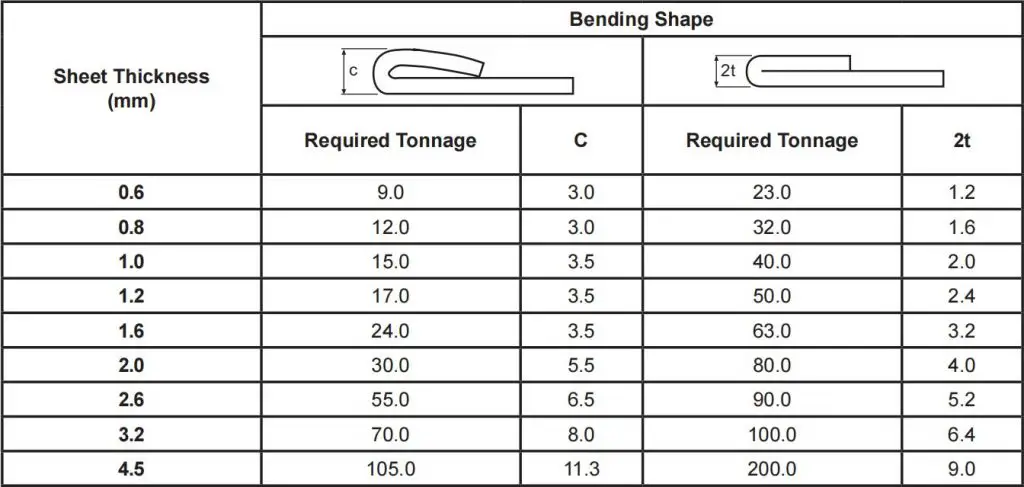
Hinweis: Die erforderliche Tonnage wird pro 1 Meter Länge angegeben.
(2) Tonnagetabelle für Säumen und Falzen von rostfreiem Stahl
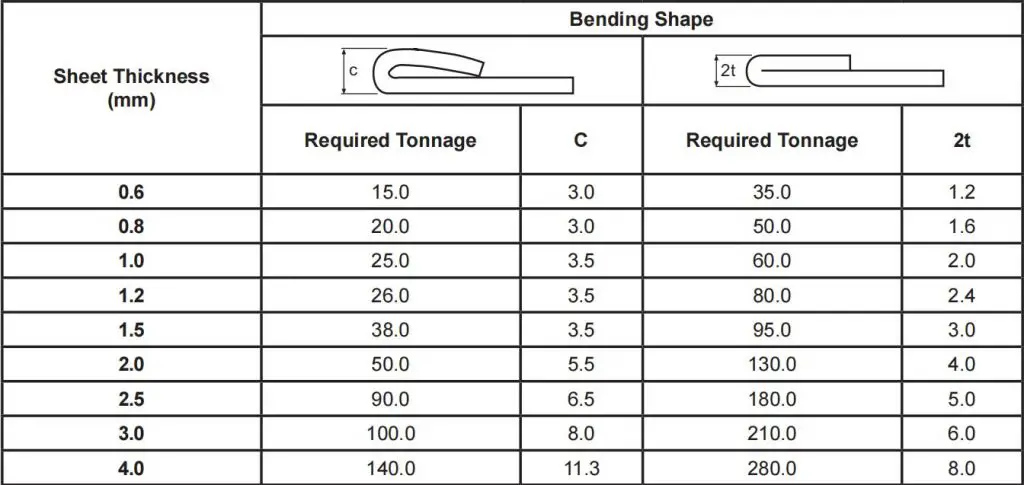
Hinweis: Die erforderliche Tonnage wird pro 1 Meter Länge angegeben.
Beim Biegen von Blechen ist an der Biegestelle ein Biegeradius erforderlich, der weder zu groß noch zu klein sein darf, sondern angemessen gewählt werden muss. Wenn der Biegeradius zu klein ist, kann es leicht zu Rissen an der Biegestelle kommen, während bei einem zu großen Biegeradius die Biegung zurückprallen kann.
Der optimale Biegeradius (innerer Biegeradius) für verschiedene Materialien mit unterschiedlichen Dicken ist in der nachstehenden Tabelle angegeben.
Mindestwert für den Biegeradius (mm)
| Materialwissenschaft | Glühen Staat | Zustand der Kaltverfestigung | ||
| Entsprechende Position zwischen Biegekurvenrichtung und Faserrichtung | ||||
| vertikal | parallel | vertikal | parallel | |
| 08, 10 | 0.1t | 0.4t | 0.4t | 0.8t |
| 15, 20 | 0.1t | 0.5t | 0.5t | 1.0t |
| 25, 30 | 0.2t | 0.6t | 0.6t | 1.2t |
| 4550 | 0.5t | 1.0t | 1.0t | 1.7t |
| 65Mn | 1.0t | 2.0t | 2.0t | 3.0t |
| Aluminium | 0.1t | 0.35t | 0.5t | 1.0t |
| Kupfer | 0.1t | 0.35t | 1.0t | 2.0t |
| Weiches Messing | 0.1t | 0.35t | 0.35t | 0.8t |
| Halbhartes Messing | 0.1t | 0.35t | 0.5t | 1.2t |
| Phosphor-Bronze | / | / | 1.0t | 3.0t |
Die Angaben in der obigen Tabelle sind optimal und dienen nur als Referenz. In der Tat beträgt die Rundung der Biegeschaufel des Herstellers in der Regel 0,3, wobei einige Biegeschaufeln eine Rundung von 0,5 aufweisen.
Für gewöhnliche Stahlplatten mit niedrigem Kohlenstoffgehalt, rostfrei AluminiumplattenBei Messing- und Kupferblechen usw. ist eine Innenrundung von 0,2 im Allgemeinen ausreichend. Für einige kohlenstoffreicher Stahlbei hartem Aluminium und superhartem Aluminium kann diese Art der Biegerundung zu Biegebrüchen oder Rissen in der Außenrundung führen.
Blechbiegeteile erfordern einen Biegeradius r an der Biegung. In der Regel ist der Biegeradius in den Plänen für Blechteile deutlich angegeben. Die endgültige Größe nach dem Biegen wird durch den Stempelradius r bestimmt0 und die Höhe der Rückfederung △r, d.h.,
r = r0 + △r.
In der Praxis liegt der Stempelradius r0 meist zwischen 0,3 und 0,5 mm, was als Konstante betrachtet werden kann und einen geringen Einfluss auf den Biegeradius hat, so dass er oft vernachlässigt werden kann. Dies bedeutet, dass der Biegeradius r eng mit der Rückfederung △r zusammenhängt.
Die Größe der Rückfederung hängt jedoch mit dem Biegedruck zusammen, der wiederum von der Matrizenschlitzbreite B und der Blechdicke t bestimmt wird. Eine Vergrößerung der Matrizenschlitzbreite B verringert den Biegedruck und erhöht die Rückfederung, während eine Verringerung von B den Biegedruck erhöht und die Rückfederung verringert.
Daher sind unter bestimmten Biegemaschinenbedingungen die Faktoren, die den Biegeradius am meisten beeinflussen, der Stempelradius r, die Matrizenschlitzbreite B und die Blechdicke t.
Die folgende Formel kann zur Berechnung der Abkantpresse verwendet werden Biegeradius:
Die minimale Innenkante ist die kürzeste Seite, die gebogen werden kann, ohne dass das Blech beim Biegen in die Fase rutscht.
Das Blech muss nämlich beim Erreichen des gewünschten Winkels auf beiden Seiten der Voute aufliegen, sonst rutscht es in die Voute hinein, was zu unbefriedigenden Ergebnissen führt.
Der minimale innere Rand kann mit der folgenden Formel berechnet werden:
Wenn der gewünschte Winkel 90° beträgt, minimaler innerer Rand = V x 0,67
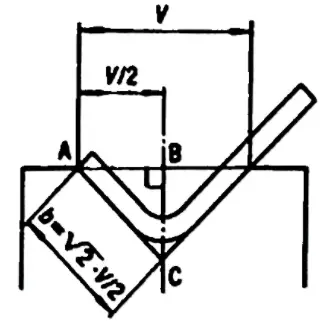
Diese Formel ergibt sich aus einer geometrischen Berechnung, da der minimale innere Rand die Diagonale eines Quadrats mit der Seite = V/2 ist. Unter Berücksichtigung des Radius wird das Ergebnis dann auf V x 0,67 angenähert.
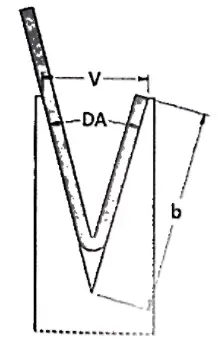
Wenn der erforderliche Winkel nicht 90° beträgt, ist auch die minimale Innenkante unterschiedlich, da die kürzeste Seite, die auf der Schräge liegen kann, vom Winkel abhängt.
Wenn ein Profil einen spitzen Winkel hat, wird das Blech weiter in die Matrizenrinne gedrückt und die Seite muss daher länger sein.
Hat ein Profil hingegen einen stumpfen Winkel, so benötigt es eine kürzere Seite, um auf einer Matrize zu liegen. Aus diesem Grund müssen Korrekturfaktoren verwendet werden, um die richtige Mindestinnenkante zu berechnen.
| Winkel | Korrektur-Faktoren |
| 30° | B = (V x 0,67) x 1,6 |
| 60° | B = (V x 0,67) x 1,1 |
| 90° | B = (V x0,67) x 1,0 |
| 120° | B = (V x 0,67) x 0,9 |
| 150° | B = (Vx 0,67) x 0,7 |
Die Berechnungsformel für die Mindestbiegekante ist für verschiedene Biegewinkel unterschiedlich und kann der folgenden Tabelle entnommen werden.
| 165° | 135° | 120° | 90° | 60° | 45° | 30° |
| 0.51×V | 0.55×V | 0.58×V | 0.71×V | 1×V | 1.31×V | 1.94×V |
L-Biegung
Referenztabelle für den inneren Biegeradius R und die Mindestbiegehöhe von kaltgewalzten dünnen Stahlplatte Materialien:
| Seriennummer | Dicke des Materials | Breite der Hohlkehle | Locher R | Minimale Biegehöhe |
| 1 | 0.5 | 4 | 0.2 | 3 |
| 2 | 0.6 | 4 | 0.2 | 3.2 |
| 3 | 0.8 | 5 | 0.8/0.2 | 3.7 |
| 4 | 1.0 | 6 | 1/0.2 | 4.4 |
| 5 | 1.2 | 8 (oder 6) | 1/0.2 | 5.5/4.5 |
| 6 | 1.5 | 10 (oder 8) | 1/0.2 | 6.8/5.8 |
| 7 | 2.0 | 12 | 1.5/0.5 | 8.3 |
| 8 | 2.5 | 16（14） | 1.5/0.5 | 10.7/9.7 |
| 9 | 3.0 | 18 | 2/0.5 | 12.1 |
| 10 | 3.5 | 20 | 2 | 13.5 |
| 11 | 4.0 | 25 | 3 | 16.5 |
Z-Biegen
Das minimale Biegemaß L für das Z-Biegen von Blechen mit unterschiedlichen Dicken ist in der nachstehenden Tabelle angegeben:
Mindesthöhe der Z-Kurve:
| Seriennummer | Dicke des Materials | Breite der Hohlkehle | Locher R | Höhe der Z-Biegung L |
| 1 | 0.5 | 4 | 0.2 | 8.5 |
| 2 | 0.6 | 4 | 0.2 | 8.8 |
| 3 | 0.8 | 5 | 0.8/0.2 | 9.5 |
| 4 | 1.0 | 6 | 1/0.2 | 10.4 |
| 5 | 1.2 | 8（6） | 1/0.2 | 11.7（10.7） |
| 6 | 1.5 | 10（8） | 1/0.2 | 13.3（12.3） |
| 7 | 2.0 | 12 | 1.5/0.5 | 14.3 |
| 8 | 2.5 | 16（14） | 1.5/0.5 | 18.2（17.2） |
| 9 | 3.0 | 18 | 2/0.5 | 20.1 |
| 10 | 3.5 | 20 | 2 | 22 |
| 11 | 4.0 | 25 | 3 | 25.5 |
Rückprallwinkel der Biegung:
Δα = b - a
wo:
b - Tatsächlicher Winkel des Werkstücks nach dem Rückprall
a - Winkel der Matrize
Größe des Rückprallwinkels:
Die Rückprallwinkel für die einwinklige 90°-Luftbiegung sind in der nachstehenden Tabelle aufgeführt.
| Material | r/t | Dicke t（mm） | ||
| <0.8 | 0.8~2 | >2 | ||
| Stahl mit niedrigem Kohlenstoffgehalt | <1 | 4° | 2° | 0° |
| Messing, σb=350MPa | 1~5 | 5° | 3° | 1° |
| Aluminium, Zink | >5 | 6° | 4° | 2° |
| Stahl mit mittlerem Kohlenstoffgehalt, σb=400-500MPa | <1 | 5° | 2° | 0° |
| Hartmessing, σb=350-400MPa | 1~5 | 6° | 3° | 1° |
| Hartes Kupfer, σb=350-400MPa | >5 | 8° | 5° | 3° |
| Stahl mit hohem Kohlenstoffgehalt, σb＞550Mpa | <1 | 7° | 4° | 2° |
| 1~5 | 9° | 5° | 3° | |
| >5 | 12° | 7° | 6° | |
Faktoren, die den Rückprall beeinflussen, und Maßnahmen zur Verringerung des Rückpralls:
Die Art des zu biegenden Materials ist entscheidend für die Bestimmung der erforderlichen Tonnage. Verschiedene Materialien weisen unterschiedliche Zugfestigkeiten auf, die sich direkt auf die zum Biegen erforderliche Kraft auswirken. Baustahl hat beispielsweise eine Zugfestigkeit von ca. 400 MPa, während nichtrostender Stahl etwa 600 MPa oder mehr erreichen kann. Dieser Unterschied bedeutet, dass zum Biegen von rostfreiem Stahl mehr Kraft erforderlich ist als bei unlegiertem Stahl. Außerdem spielt die Dicke des Materials eine wichtige Rolle; dickere Materialien erfordern exponentiell mehr Kraft, um die gewünschte Biegung zu erreichen. Ein 10 mm dickes Edelstahlblech erfordert eine wesentlich höhere Tonnage als ein 2 mm dickes.
Die Materialstärke ist direkt proportional zur erforderlichen Tonnage. Dickere Materialien erfordern mehr Kraft zum Biegen. Diese Beziehung ist nicht linear, sondern exponentiell; eine Verdoppelung der Materialdicke bedeutet mehr als eine Verdoppelung der erforderlichen Tonnage. Wenn zum Beispiel für ein 5 mm dickes Blech 50 Tonnen Kraft erforderlich sind, kann ein 10 mm dickes Blech mehr als 100 Tonnen erfordern. Daher ist die genaue Messung und Berücksichtigung der Materialdicke für die Tonnageberechnung unerlässlich.
Die Größe der Matrizenöffnung bzw. der V-Matrize ist ein entscheidender Faktor für die Tonnageanforderungen. Kleinere Matrizenöffnungen erfordern eine höhere Tonnage, da das Material in einen engeren Raum gepresst werden muss, was den Widerstand erhöht. So kann beispielsweise eine 30-Grad-Matrizenöffnung bei gleichem Material und gleicher Dicke weniger Kraft erfordern als eine 10-Grad-Matrizenöffnung. Umgekehrt erfordern größere Matrizenöffnungen weniger Kraft, was den Biegevorgang erleichtert.
Verschiedene Biegemethoden erfordern einen unterschiedlichen Kraftaufwand. Luftbiegen, Gesenkbiegen und Prägen sind die drei wichtigsten Methoden, die bei Abkantpressen zum Einsatz kommen. Beim Luftbiegen wird das Material in eine V-Matrize gepresst, jedoch nicht vollständig, was den geringsten Kraftaufwand erfordert. Bei dieser Methode ist eine gewisse Rückfederung möglich, die im Endwinkel berücksichtigt werden muss. Das untere Biegen, bei dem das Material ganz bis zum Boden der Matrize gepresst wird, erfordert aufgrund des erhöhten Materialwiderstands mehr Kraft. Beim Prägen, dem kraftintensivsten Verfahren, wird das Material vollständig in die Matrize gepresst, wodurch präzise Biegungen mit minimaler Rückfederung möglich sind. Die jeweilige Wirkung auf das Material bestimmt die benötigte Tonnage.
Die Art und der Zustand der Werkzeuge, die bei Abkantarbeiten verwendet werden, wirken sich ebenfalls auf die Tonnageberechnung aus. Verschiedene Arten von Matrizen und Stempeln haben unterschiedliche Kraftanforderungen. Beispielsweise müssen Schwanenhalswerkzeuge, die so konstruiert sind, dass sie nicht mit dem Werkstück kollidieren, vorsichtig gehandhabt werden, um eine zu hohe Tonnage zu vermeiden, was zu Schäden an der Ausrüstung führen kann. Gut gewartete Werkzeuge gewährleisten eine genauere und effizientere Biegung, während abgenutzte oder beschädigte Werkzeuge die erforderliche Kraft erhöhen und die Qualität der Biegung beeinträchtigen können.
Es ist wichtig, die Kapazität der Abkantpresse selbst zu berücksichtigen. Die berechnete Tonnage sollte die Nennkapazität der Maschine nicht überschreiten, da eine Überlastung zu Schäden an der Ausrüstung führen kann, z. B. zur Verformung von Bett oder Stößel. Wenn Sie sicherstellen, dass die Abkantpresse innerhalb ihrer Kapazität arbeitet, beugen Sie nicht nur Schäden vor, sondern verlängern auch die Lebensdauer der Maschine. Wenn eine Abkantpresse beispielsweise für 100 Tonnen ausgelegt ist, muss die erforderliche Tonnage für jeden Auftrag sorgfältig berechnet werden, um eine Überschreitung dieser Grenze zu vermeiden.
Umgebungsbedingungen wie Temperatur und Luftfeuchtigkeit können die Materialeigenschaften und damit auch die erforderliche Tonnage beeinflussen. Zum Beispiel können Materialien bei kälteren Temperaturen spröder werden, was eine andere Handhabung und Kraftanpassung erfordert. Außerdem kann sich die Luftfeuchtigkeit auf bestimmte Materialien auswirken, z. B. Aluminium, das Feuchtigkeit aufnehmen und seine Eigenschaften verändern kann. Die Berücksichtigung dieser Faktoren gewährleistet genauere und zuverlässigere Biegevorgänge.
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
AR 
ES 
FR 
ID 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR