Haben Sie sich schon einmal gefragt, warum sich manche Materialien leicht biegen lassen, während andere starr bleiben? Dieser Blog taucht in die faszinierende Welt des Elastizitätsmoduls und der Steifigkeit ein und enträtselt ihre entscheidende Rolle in der Technik. Am Ende werden Sie verstehen, wie diese Eigenschaften die Festigkeit und Flexibilität von Alltagsmaterialien beeinflussen.
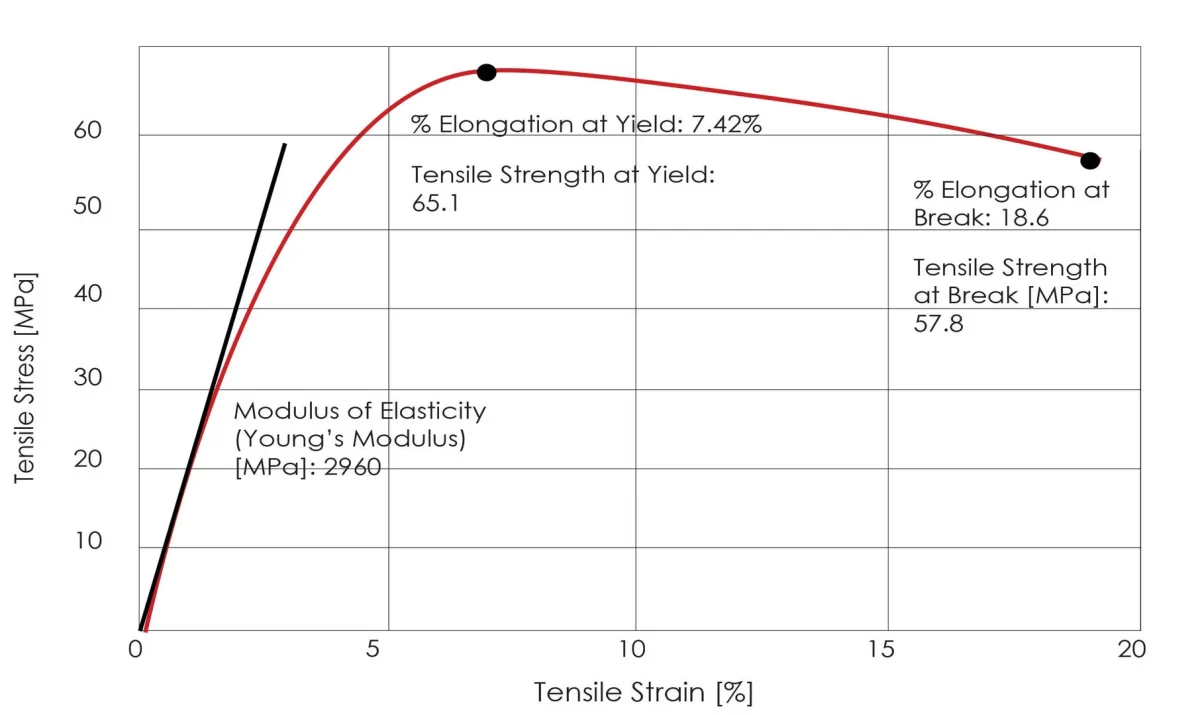
Elastizitätsmodul: Das Verhältnis der Normalspannung zur entsprechenden Normaldehnung im Stadium der elastischen Verformung eines Materials.
In der Phase der elastischen Verformung sind Spannung und Dehnung eines Materials gemäß dem Hookeschen Gesetz proportional, und der Proportionalitätskoeffizient wird als Elastizitätsmodul bezeichnet.
Der Begriff "Elastizitätsmodul" ist eine allgemeine Beschreibung der Elastizität eines Materials. Er umfasst mehrere spezifische Module, darunter den Elastizitätsmodul, den Schermodul und den Kompressionsmodul, um nur einige zu nennen.
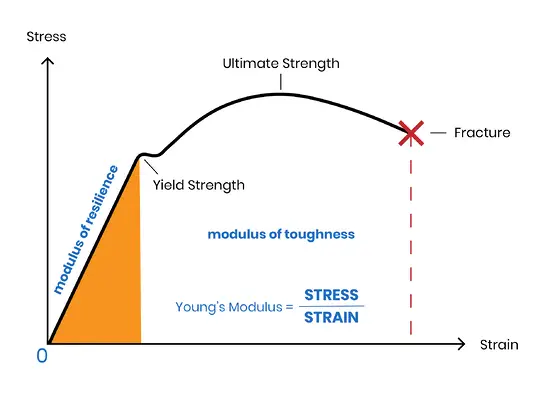
Daher sind die Begriffe "Elastizitätsmodul" und "Volumenmodul" umfassend.
Wenn eine äußere Kraft (bekannt als "Spannung") auf ein Elastomer einwirkt, ändert es seine Form (bekannt als "Dehnung"). Der Elastizitätsmodul ist definiert als das Verhältnis von Spannung zu Dehnung.
Zum Beispiel:
Lineare Dehnung:
Wenn eine Zugkraft F auf einen dünnen Stab ausgeübt wird, wird die lineare Spannung als Zugkraft geteilt durch die Querschnittsfläche S des Stabes berechnet.
Die lineare Dehnung wird berechnet als die Dehnung des Stabes (dL) geteilt durch seine ursprüngliche Länge (L).
Die lineare Spannung geteilt durch die lineare Dehnung ist gleich dem Elastizitätsmodul E = (F / S) / (dL / L).
Scherdehnung:
Wenn eine seitliche Kraft (in der Regel eine Reibungskraft) f auf ein Elastomer einwirkt, ändert sich dessen Form von einer quadratischen in eine rautenförmige.
Dieser Verformungswinkel wird als "Scherdehnung" bezeichnet, und die entsprechende Kraft geteilt durch die Spannungsfläche wird als "Schubspannung" bezeichnet.
Die Scherspannung geteilt durch die Scherdehnung ist gleich dem Schermodul G = (f / S) / a.
Volumenbelastung:
Wenn ein Gesamtdruck P auf das Elastomer ausgeübt wird, spricht man von einer "Volumenspannung".
Die Volumenverringerung des Elastomers (-dV) geteilt durch sein ursprüngliches Volumen (V) wird als "Volumendehnung" bezeichnet.
Die Volumenspannung geteilt durch die Volumendehnung ist gleich dem Volumenmodul K = P / (-dV / V).
Im Allgemeinen bezieht sich der Elastizitätsmodul von metallischen Werkstoffen auf den Elastizitätsmodul, der auch als positiver Elastizitätsmodul bezeichnet wird, wenn es keine Verwechslungen gibt.
Einheit: E (Elastizitätsmodul) wird in GPa gemessen.
Der Elastizitätsmodul ist ein entscheidender Leistungsparameter von technischen Werkstoffen.
Aus der Makroperspektive misst sie die Fähigkeit eines Objekts, elastischer Verformung zu widerstehen, während sie aus der Mikroperspektive die Bindungsstärke zwischen Atomen, Ionen oder Molekülen widerspiegelt.
Faktoren, die die Haftfestigkeit beeinflussen, können sich auch auf den Elastizitätsmodul eines Materials auswirken, wie z. B. die Art der Bindung, die Kristallstruktur, die chemische Zusammensetzung, die Mikrostruktur, die Temperatur und andere.
Der Elastizitätsmodul von metallische Werkstoffe kann aufgrund unterschiedlicher Legierungszusammensetzungen, Wärmebehandlungszustände und plastischer Kaltverformungen um über 5% schwanken.
Im Allgemeinen ist jedoch der Elastizitätsmodul von metallische Werkstoffe ist ein strukturunabhängiger Index für mechanische Eigenschaften.
Die Legierung, die Wärmebehandlung (Faserstruktur) und die plastische Kaltverformung haben nur begrenzte Auswirkungen auf den Elastizitätsmodul, und externe Faktoren wie Temperatur und Belastungsgeschwindigkeit haben nur einen geringen Einfluss auf ihn.
Daher wird der Elastizitätsmodul in allgemeinen technischen Anwendungen als konstant angesehen.
Einheit: GPa (Gigapascal) für den Elastizitätsmodul.
Der Elastizitätsmodul ist ein Maß für den Widerstand eines Materials gegen elastische Verformung.
Je höher dieser Wert ist, desto größer ist die Spannung, die erforderlich ist, um eine bestimmte elastische Verformung zu erzeugen, d. h. das Material ist steifer und erfährt bei einer bestimmten Spannung weniger elastische Verformung.
Der Elastizitätsmodul, dargestellt durch E, ist ein Maß für die Spannung, die ein Material benötigt, um sich unter einer äußeren Kraft um eine Einheit elastisch zu verformen.
Sie stellt die Fähigkeit des Materials dar, elastischer Verformung zu widerstehen und kann mit der Steifigkeit von eine Feder.
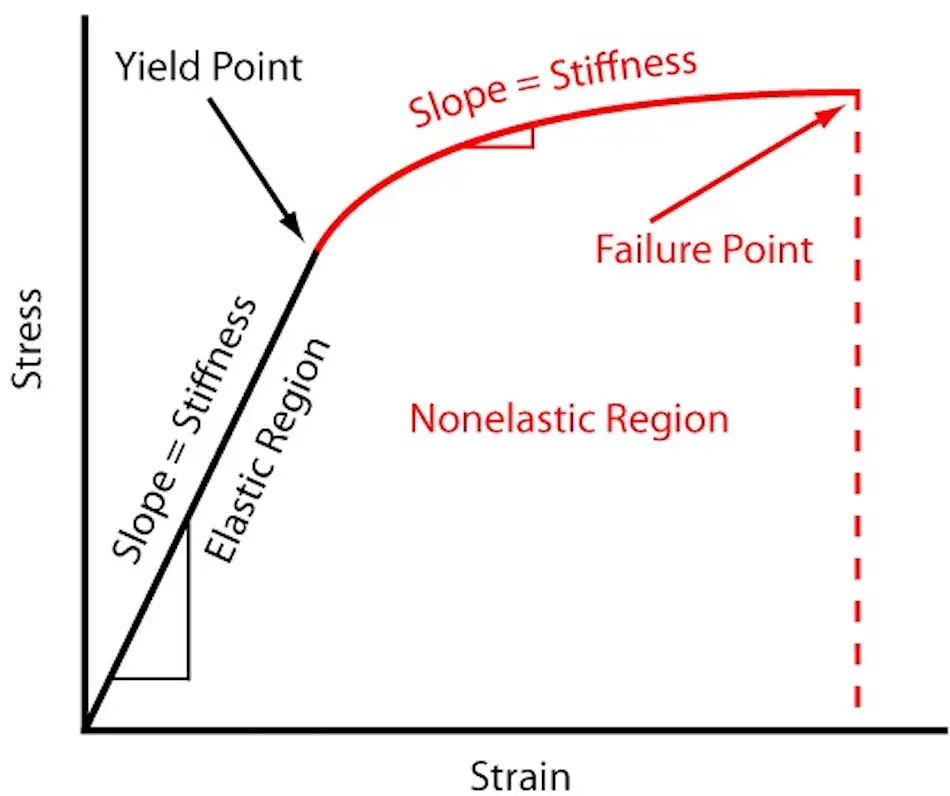
Steifigkeit" bezieht sich auf die Fähigkeit einer Struktur oder eines Bauteils, elastischer Verformung zu widerstehen. Sie wird durch die Kraft oder das Moment bestimmt, die bzw. das erforderlich ist, um eine Einheit der Dehnung zu erzeugen.
Die Rotationssteifigkeit wird durch "k" dargestellt und kann als "k = M / θ" berechnet werden, wobei "M" das aufgebrachte Drehmoment und "θ" der Drehwinkel ist.
Andere Steifigkeitswerte sind:
Die Methode zur Berechnung der Steifigkeit kann in zwei Ansätze unterteilt werden: die Theorie der kleinen Verschiebung und die Theorie der großen Verschiebung.
Die Theorie der großen Verdrängung berücksichtigt die Verformung der Struktur nach der Beanspruchung und bildet entsprechend die Gleichgewichtsgleichung, die genaue Ergebnisse liefert, aber einen komplexeren Berechnungsprozess erfordert.
Im Gegensatz dazu geht die Theorie der kleinen Verformung davon aus, dass die Struktur nicht wesentlich verformt wird, so dass die innere Kraft aus der äußeren Last ermittelt und dann zur Berechnung der Verformung verwendet werden kann.
Dieser Ansatz ist in den meisten mechanischen Konstruktionsanwendungen weit verbreitet, da er viel einfacher zu lösen ist.
Bei der Berechnung der Biegeverformung von Balken wird beispielsweise häufig die Theorie der kleinen Verschiebung verwendet, da die tatsächliche Verformung sehr gering ist.
Bei dieser Theorie wird die erste Ableitung der Durchbiegung in der Krümmungsformel ignoriert und die zweite Ableitung der Durchbiegung zur Annäherung an die Krümmung der Balkenachse verwendet, was zur Vereinfachung des Lösungsprozesses durch Linearisierung der Differentialgleichung beiträgt.
Wenn mehrere Lasten gleichzeitig einwirken, kann die von jeder Last verursachte Biegeverformung separat berechnet und dann kombiniert werden.
Der Verformungswiderstand bei statischer Belastung wird als statische Steifigkeit bezeichnet, während der Verformungswiderstand bei dynamischer Belastung als dynamische Steifigkeit bezeichnet wird, d. h. der Betrag der für eine Amplitudeneinheit erforderlichen dynamischen Kraft.
Wenn sich die störende Kraft langsam ändert (d. h. die Frequenz der störenden Kraft ist viel kleiner als die Eigenfrequenz der Struktur), ist die dynamische Steifigkeit im Wesentlichen gleich der statischen Steifigkeit.
Ändert sich die Störkraft jedoch schnell (d. h. die Frequenz der Störkraft ist viel größer als die Eigenfrequenz der Struktur), ist die strukturelle Verformung relativ klein und damit die dynamische Steifigkeit relativ groß.
Liegt die Frequenz der Störkraft in der Nähe der Eigenfrequenz des Bauwerks, tritt Resonanz auf, und die dynamische Steifigkeit ist am geringsten, so dass sich das Bauwerk am leichtesten verformen lässt und seine dynamische Verformung das Mehrfache oder sogar mehr als das Zehnfache der statischen Lastverformung erreichen kann.
Eine übermäßige Verformung von Bauteilen kann sich auf deren Funktion auswirken.
So kann beispielsweise eine übermäßige Verformung einer Getriebewelle den Zahneingriff beeinträchtigen, und eine übermäßige Verformung einer Werkzeugmaschine kann die Bearbeitungsgenauigkeit verringern.
Zu den Faktoren, die die Steifigkeit beeinflussen, gehören der Elastizitätsmodul der Materialien und die Form der Struktur. Eine Änderung der Strukturform kann sich erheblich auf die Steifigkeit auswirken.
Die Berechnung der Steifigkeit ist die Grundlage der Schwingungstheorie und der Analyse der strukturellen Stabilität. Wenn die Masse konstant bleibt, führt eine hohe Steifigkeit zu einer hohen Eigenfrequenz.
Die Spannungsverteilung in einer statisch unbestimmten Struktur hängt mit dem Steifigkeitsverhältnis der einzelnen Teile zusammen.
Unter Bruchmechanik Analyse kann der Spannungsintensitätsfaktor eines gerissenen Bauteils auf der Grundlage seiner Flexibilität bestimmt werden.
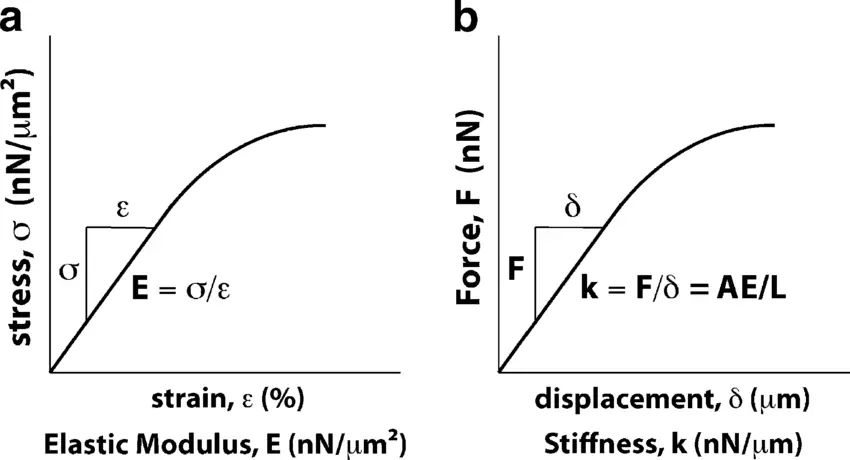
Steifigkeit und Elastizitätsmodul sind grundlegende Konzepte in der Materialwissenschaft, die jeweils unterschiedliche Aspekte der Verformungsbeständigkeit eines Materials beschreiben. Obwohl sie miteinander verwandt sind, spielen sie bei der Analyse und Anwendung von Werkstoffen eine unterschiedliche Rolle.
Der Elastizitätsmodul, auch bekannt als Elastizitätsmodul, ist ein spezifisches Maß für die einem Material innewohnende Fähigkeit, Verformungen unter Spannung zu widerstehen. Er quantifiziert das Verhältnis zwischen Spannung (Kraft pro Flächeneinheit) und Dehnung (proportionale Verformung) im linear elastischen Bereich der Spannungs-Dehnungskurve des Materials. Der Elastizitätsmodul ist eine Materialeigenschaft und ist unabhängig von der Form oder Größe des Materials. Er wird in Druckeinheiten, z. B. Pascal (Pa), ausgedrückt.
Steifigkeit hingegen ist ein weiter gefasster Begriff, der sich auf den Widerstand einer Struktur gegen elastische Verformung unter einer einwirkenden Last bezieht. Sie ist nicht nur eine Materialeigenschaft, sondern hängt auch von der Geometrie und den Randbedingungen der Struktur ab. Die Steifigkeit wird in der Regel als die Kraft ausgedrückt, die erforderlich ist, um eine Verschiebungseinheit zu erreichen (z. B. Newton pro Meter, N/m).
Die Steifigkeit eines Bauteils lässt sich aus dem Elastizitätsmodul des Materials und der Geometrie des Elements ableiten. So ist beispielsweise die Biegesteifigkeit (EI) eines Trägers das Produkt aus dem Elastizitätsmodul (E) und dem Trägheitsmoment (I) des Trägerquerschnitts. In ähnlicher Weise ist die Torsionssteifigkeit (GI) das Produkt aus dem Schubmodul (G) und dem polaren Trägheitsmoment (I).
Die Steifigkeit ist bei der Konstruktion von entscheidender Bedeutung, insbesondere für Bauteile, die ihre Form unter Belastung beibehalten müssen, wie Spindeln, Führungsschienen und Gewindespindeln. Auch für Strukturen, die eine strenge Verformungskontrolle erfordern, wie z. B. Flugzeugflügel und hochpräzise Baugruppen, ist sie unerlässlich.
Festigkeit ist die Fähigkeit eines Materials, einer dauerhaften Verformung und einem Bruch unter Einwirkung äußerer Kräfte zu widerstehen. Sie umfasst verschiedene Arten der Festigkeit, darunter Streckgrenze, Zugfestigkeit, Druckfestigkeit und Biegefestigkeit. Diese Eigenschaften sind entscheidend für die Tragfähigkeit und Haltbarkeit von mechanischen Teilen.
Das Verständnis des Unterschieds zwischen Steifigkeit und Elastizitätsmodul ist für die Konstruktion und Analyse mechanischer Komponenten und Strukturen von entscheidender Bedeutung. Während der Elastizitätsmodul ein Maß für den intrinsischen Widerstand eines Materials gegen Verformung ist, berücksichtigt die Steifigkeit sowohl Materialeigenschaften als auch geometrische Faktoren, um den Gesamtwiderstand einer Struktur gegen Verformung zu beschreiben. Beide Konzepte sind für die Gewährleistung der Leistung und Zuverlässigkeit technischer Konstruktionen unerlässlich.
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
AR 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO