In diesem Artikel befassen wir uns mit innovativen zerstörungsfreien Prüfverfahren, die die wahre Güte und Festigkeit von Stahlkonstruktionen aufzeigen. Erfahren Sie, wie Wissenschaftler Härtetests und empirische Formeln einsetzen, um die Sicherheit und Zuverlässigkeit von Bauprojekten zu gewährleisten. Tauchen Sie ein und entdecken Sie die faszinierende Wissenschaft hinter diesen Techniken!
Eine genaue Bewertung der Qualität von Stahlkonstruktionen im Einsatz erfordert die Bestimmung der Stahlsorte und der Festigkeit des Stahls. Dies ist die Grundlage für eine zuverlässige Prüfung und Bewertung.
Die herkömmliche Methode zur Bestimmung der Stahlfestigkeit ist die Entnahme von Proben aus dem Bauwerk für Zugversuche, aber dieses Verfahren kann das ursprüngliche Bauwerk beschädigen und ist bei bestimmten Bauwerken nicht praktikabel.
Daher ist es von entscheidender Bedeutung, zerstörungsfreie Prüfverfahren zur Berechnung der Stahlsorte und -festigkeit einzusetzen.
Forscher aus dem In- und Ausland haben zerstörungsfreie Prüfverfahren zur Bestimmung der Stahlfestigkeit auf Baustellen untersucht. Sie haben sich hauptsächlich auf die chemische Zusammensetzung und die Härte konzentriert und einige empirische Formeln entwickelt.
Weiterführende Lektüre: Metallhärte: Der definitive Leitfaden (mit Härtetabelle)
Diese empirischen Formeln können in zwei Typen unterteilt werden:
Bei der ersten Variante wird die Zugfestigkeit auf der Grundlage der chemischen Zusammensetzung berechnet, wie in der Formel in GB/T 50621-2010 Technical Standard for On-site Testing of Steel Structures angegeben. Die Festigkeit von Stahlwerkstoffen wird jedoch durch die chemische Zusammensetzung und den Herstellungsprozess (z. B. Gießen, Schmieden, Walzen und Wärmebehandlung) beeinflusst, so dass die Berechnung der Stahlfestigkeit allein anhand der chemischen Zusammensetzung zu erheblichen Abweichungen führen kann.
Bei der zweiten Art wird die Zugfestigkeit auf der Grundlage der Härte berechnet. Die Forschung hat gezeigt, dass es eine positive Korrelation zwischen der Härte und der Zugfestigkeit von Stahl gibt. Die Zugfestigkeit Festigkeit von Werkstoffen kann anhand der Ergebnisse von Härtetests geschätzt werden, was in der technischen Praxis eine weit verbreitete Methode ist.
Derzeit sind die wichtigsten inländischen Normen, die für diesen Zweck verwendet werden können, GB/T 33362-2016 Conversion of Hardness Values of Metallische Werkstoffe und GB/T 1172-1999 Umrechnung von Härte und Festigkeit von Eisenmetallen. GB/T 33362-2016 ist äquivalent zu ISO 18265:2013 Umrechnung von Härtewerten metallischer Werkstoffe. Die Härteumrechnungstabelle für unlegierten Stahl, niedrig legierten Stahl und Stahlguss in Tabelle A.1 dieser Norm wurde durch Vergleichsprüfungen mit geprüften und kalibrierten Härtemessgeräten in verschiedenen Laboratorien durch den Deutschen Verband der Metallurgischen Ingenieure ermittelt. GB/T 1172-1999 wurde durch umfangreiche Tests und Forschungsarbeiten von Institutionen wie der China Academy of Metrology erstellt. Tabelle 2 in der Norm enthält hauptsächlich das Umrechnungsverhältnis für kohlenstoffarmen Stahl.
Keine dieser Normen liefert jedoch verlässliche Daten mit statistischer Signifikanz für die Unsicherheit der Umrechnungswerte, und die Schwankungsbreite der Umrechnungsergebnisse ist unbekannt. Die Forscher haben die Korrelation zwischen Härte und Festigkeit von Stahl, der beim Bau von Stahlkonstruktionen verwendet wird, durch Regressionsanalyse untersucht und mit nationalen Normen verglichen, was als Überprüfung und Ergänzung der Normen GB/T 33362-2016 und GB/T 1172-1999 dient. Sie haben auch die Nachweismethode erörtert, die für die Baustellen von Stahlkonstruktionen geeignet ist und die vorhandenen tragbaren Nachweissysteme einbezieht.
Die Forschungsobjekte dieser Studie sind die im Stahlbau häufig verwendeten Stahlbleche Q235 und Q345.
Verwandte Lektüre: Q235 vs. Q345 Stahl
Um repräsentative Proben zu erhalten, wurden 162 Stahlplatten von 86 Stahlkonstruktionsherstellern in der Provinz Jiangsu gesammelt, darunter 82 Stück Q235-Stahlplatten und 80 Stück Q345-Stahlplatten. Die Dicke der Stahlplatten betrug 6, 8, 10, 12, 14, 18, 20 und 30 mm.
Die Stahlplatten wurden zu 20mm x 400mm großen Streifenproben verarbeitet und die Zugversuche wurden mit einer mikrocomputergesteuerten elektrohydraulischen Servo-Zugprüfmaschine gemäß den Anforderungen von GB/T 228.1-2010 durchgeführt.
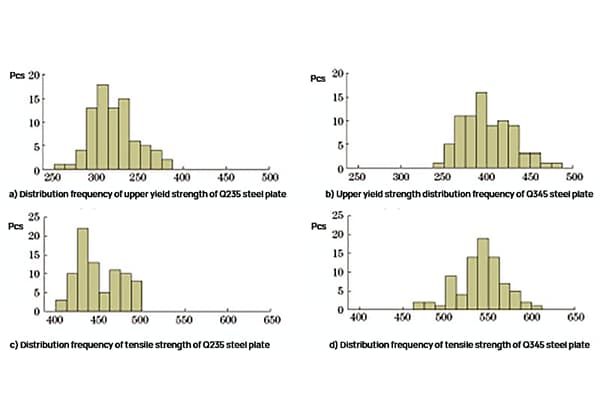
Die Testergebnisse der oberen Streckgrenze und die Zugfestigkeit der Q235- und Q345-Stahlplatten wurden statistisch ausgewertet, und die Häufigkeitsverteilung ist in Abbildung 1 dargestellt.
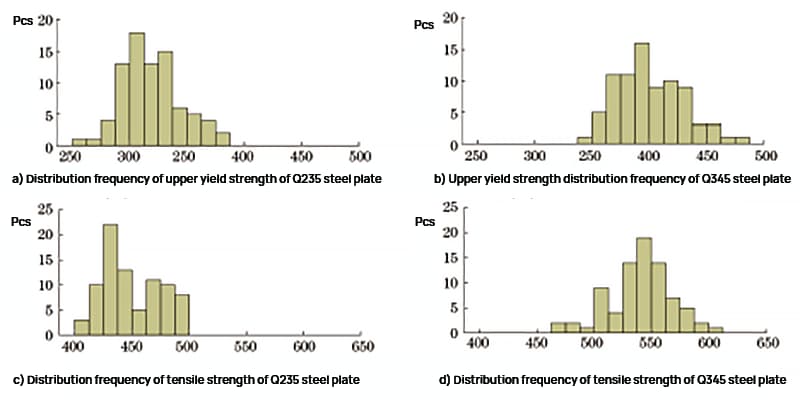
Abb. 1 Häufigkeit der Festigkeitsverteilung von Q235 Stahlplatte und Q345 Stahlplatten
Wie in Abbildung 1 dargestellt, liegt der obere Streckgrenzenbereich des Q235-Stahlblechs bei 261 bis 382 MPa, und der Zugfestigkeitsbereich beträgt 404 bis 497 MPa. Der obere Streckgrenzenbereich des Q345-Stahlblechs liegt bei 345 bis 477 MPa, und der Zugfestigkeitsbereich beträgt 473 bis 607 MPa.
Die Häufigkeitsverteilung der Intensität ist annähernd normal, und die Testergebnisse stimmen mit den täglichen Inspektionsdaten überein, was darauf hindeutet, dass die Proben sehr repräsentativ sind.
Die Prüfmuster wurden gemäß den Normvorgaben entnommen und bearbeitet sowie Rockwell-Härte, Vickers-Härte, Brinell-Härte und Zugversuche unterzogen.
Zur Durchführung der Regressionsanalyse der Härte- und Festigkeitsprüfergebnisse wurde die Methode der kleinsten Quadrate verwendet und die Software SPSS eingesetzt.
2.1.1 Ergebnisse und Analyse der Rockwell-Härteprüfung
Die Oberfläche der Probe wurde mit einer Schleifmaschine geschliffen, um sicherzustellen, dass sie eben und glatt ist. Es wurde die Skala B gewählt und das Gerät wurde mit einem Standard-Härteblock kalibriert. Die Rockwell-Härteprüfung wurde in Übereinstimmung mit den Anforderungen von GB/T 230.1-2018 Metallic Materials Rockwell Hardness Test Part 1: Test Method durchgeführt. Für jede Probe wurden drei Punkte gemessen, und der Durchschnittswert wurde ermittelt.
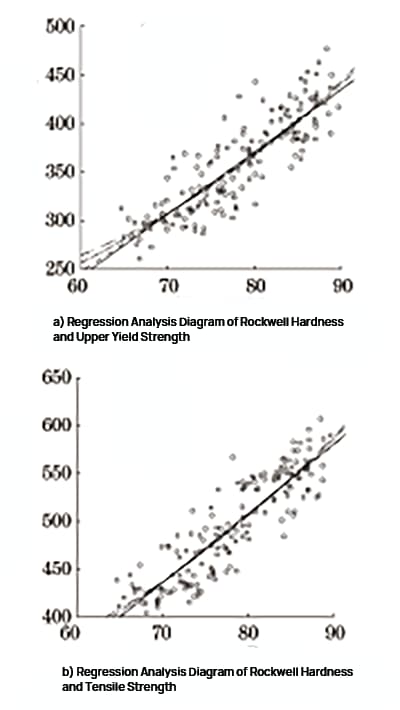
Abb. 2 Regressionsanalyse von Rockwell-Härte und Festigkeit
Die SPSS-Software wurde verwendet, um eine lineare Regression, eine quadratische Regression, eine Potenzregression und eine exponentielle Regressionsanalyse für die Rockwell-Härte, die obere Streckgrenze und die Zugfestigkeit durchzuführen. Das Diagramm der Regressionsanalyse ist in Abbildung 2 dargestellt, und die Ergebnisse der Regressionsanalyse sind in Tabelle 1 und Tabelle 2 aufgeführt.
Tabelle 1: Regressionsmodelldaten der Rockwellhärte und der oberen Streckgrenze
| Gleichung | Modell Zusammenfassung | Modellparameter | ||||
| R2 | F | Signifikanz P | Konstante | b1 | b2 | |
| Linearer quadratischer Exponent | 0.736 | 446.897 | 0.000 | -143.077 | 6.426 | 0.081 |
| 0.741 | 227.290 | 0.000 | 341.852 | -6.141 | ||
| 0.740 | 456.461 | 0.000 | 0.828 | 1.392 | ||
| 0.744 | 464.965 | 0.000 | 86.806 | 0.018 | ||
Tabelle 2: Regressionsmodelldaten für Rockwell-Härte und Zugfestigkeit
| Gleichung | Modell Zusammenfassung | Modellparameter | ||||
| R2 | F | Signifikanz P | Konstante | b1 | b2 | |
| Linearer quadratischer Exponent | 0.780 | 565.900 | 0.000 | -71.394 | 7.241 | 0.074 |
| 0.783 | 286.412 | 0.000 | 372.980 | -4.274 | ||
| 0.778 | 560.887 | 0.000 | 3.477 | 1.137 | ||
| 0.782 | 574.207 | 0.000 | 155.315 | 0.015 | ||
Wie aus Tabelle 1 und Tabelle 2 hervorgeht, korreliert die Rockwell-Härte stark mit der Festigkeit, und die Korrelation mit der Zugfestigkeit ist im Vergleich zur oberen Streckgrenze stärker.
Von den vier Regressionsmodellen zwischen Rockwell-Härte und Festigkeit haben alle eine Signifikanz P kleiner als 0,05 und eine enge Anpassungsgüte R2.
Da die in der Norm angegebene Umrechnungsbeziehung zwischen Rockwell-Härte und Zugfestigkeit von Stahl mit niedrigem Kohlenstoffgehalt dem Polynommodell ähnelt, wird empfohlen, das quadratische Modell für die Umrechnung zu verwenden.
Die Formel nach der Anpassung lautet:
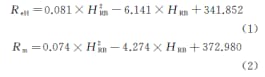
Wo: ReH ist die obere Streckgrenze; Rm ist die Zugfestigkeit; HRB ist die Rockwell-Härte.
2.1.2 Analyse der relativen Abweichung der Umrechnungsergebnisse
Auf der Grundlage des angepassten quadratischen Regressionsmodells wurden die relativen Abweichungen zwischen den umgerechneten Werten der oberen Streckgrenze und der Zugfestigkeit und den Ergebnissen des Zugversuchs berechnet und statistisch ausgewertet. Die Stichprobengröße betrug 162, und die Ergebnisse sind in Tabelle 3 dargestellt.
Die relativen Abweichungen folgen einer Normalverteilung, und die Häufigkeitsverteilung ist in Abbildung 3 dargestellt.
Tabelle 3 Statistische Tabelle der relativen Abweichung von der Rockwell-Härte zur Festigkeit
| Statistische Positionen | Minimaler Wert | Maximum | Durchschnittliche Abweichung | Standard-Referenz |
| Relative Abweichung des oberen Umrechnungswertes der Streckgrenze | -16.56 | +16.61 | ±5.46 | 6.84 |
| Relative Abweichung der umgerechneten Zugfestigkeit | -13.31 | +11.16 | ±4.12 | 5.03 |
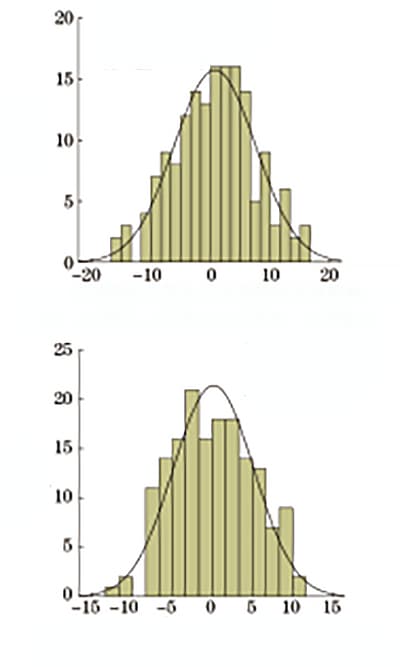
Abb. 3 Relative Abweichung von der Rockwell-Härte zur Festigkeit
2.1.3 Vergleich mit dem nationalen Standardumrechnungswert
Abbildung 4 zeigt einen Vergleich des in der Norm angegebenen Umrechnungswerts der Zugfestigkeit, des Umrechnungswerts der angepassten quadratischen Regressionsformel und des Streudiagramms der entsprechenden Beziehung zwischen Rockwell-Härte und Zugfestigkeit in ein und demselben Diagramm.
Abb. 4 Vergleichstabelle der Zugfestigkeit umgerechnet in Rockwell-Härte
Wie aus Abbildung 4 ersichtlich, ist der Gesamttrend der drei Kurven konsistent. Der in GB/T 1172-1999 angegebene Umrechnungswert der Zugfestigkeit ist ähnlich wie der des Autors, mit einer durchschnittlichen Abweichung von 2,7% und einer maximalen Abweichung von 5,7% im Bereich von 370 bis 630 MPa.
Der in GB/T 33362-2016 angegebene Umrechnungswert der Zugfestigkeit ist jedoch niedriger für Q235-Stahl (mit einer Zugfestigkeit im Bereich von 370 bis 500 MPa) und höher für Q345-Stahl (mit einer Zugfestigkeit im Bereich von 470 bis 630 MPa).
2.2.1 Ablauf der Vickers-Härteprüfung und Ergebnisanalyse
Die Oberfläche der Probe wurde mit einer Schleifmaschine poliert, und das Gerät wurde mit einem Standardhärteblock kalibriert. Die Vickers-Härteprüfung wurde gemäß den Anforderungen der GB/T 4340.1-2009 Metallic Materials Vickers Hardness Test Part 1: Test Method durchgeführt. Für jede Probe wurden drei Punkte gemessen, und der Durchschnittswert wurde ermittelt.
SPSS-Software wurde verwendet, um eine lineare Regression, eine quadratische Regression, eine Potenzregression und eine exponentielle Regressionsanalyse der Vickershärte, der oberen Streckgrenze und der Zugfestigkeit durchzuführen. Das Diagramm der Regressionsanalyse ist in Abbildung 5 dargestellt, und die Ergebnisse der Regressionsanalyse sind in Tabelle 4 und Tabelle 5 aufgeführt.
Tabelle 4: Regressionsmodell für die Vickershärte und die obere Streckgrenze
| Gleichung | Modell Zusammenfassung | Modellparameter | ||||
| R2 | F | Signifikanz P | Konstante | b1 | b2 | |
| Linearer quadratischer Exponent | 0.727 | 426.980 | 0.000 | -9.332 | 2.530 | 0.002 |
| 0.728 | 212.272 | 0.000 | 27.358 | 2.020 | ||
| 0.731 | 433.768 | 0.000 | 2.215 | 1.021 | ||
| 0.731 | 435.083 | 0.000 | 126.740 | 0.007 | ||
Abb. 5 Regressionsanalyse von Vickershärte und Festigkeit
Tabelle 5: Regressionsmodell für die Vickershärte und die Zugfestigkeit
| Gleichung | Modell Zusammenfassung | Modellparameter | ||||
| R2 | F | Signifikanz P | Konstante | b1 | b2 | |
| Linearer quadratischer Exponent | 0.753 | 486.507 | 0.000 | 84.099 | 2.818 | 0.002 |
| 0.753 | 241.944 | 0.000 | 133.182 | 2.136 | ||
| 0.748 | 475.262 | 0.000 | 8.189 | 0.823 | ||
| 0.751 | 483.330 | 0.000 | 213.597 | 0.006 | ||
Wie aus Tabelle 4 und Tabelle 5 hervorgeht, weist die Vickershärte eine starke Korrelation mit der Festigkeit auf, und die Korrelation mit der Zugfestigkeit ist im Vergleich zur oberen Streckgrenze stärker.
Von den vier Regressionsmodellen zwischen Vickershärte und Festigkeit haben alle eine Signifikanz P kleiner als 0,05 und eine enge Anpassungsgüte R2.
Da die in der Norm angegebene Umrechnungsbeziehung zwischen Vickershärte und Zugfestigkeit von Stahl mit niedrigem Kohlenstoffgehalt einer linearen Beziehung nahekommt, wird empfohlen, die lineare Beziehung für die Umrechnung zu verwenden.
Die Formel nach der Anpassung lautet:
Wo: HV ist die Vickershärte.
2.2.2 Analyse der relativen Abweichung der Umrechnungsergebnisse
Auf der Grundlage des angepassten linearen Regressionsmodells wurden die relativen Abweichungen zwischen den umgerechneten Werten der oberen Streckgrenze und der Zugfestigkeit und den Ergebnissen des Zugversuchs berechnet und statistisch ausgewertet. Die Stichprobengröße betrug 162, und die Ergebnisse sind in Tabelle 6 dargestellt.
Die relativen Abweichungen folgen einer Normalverteilung, und die Häufigkeitsverteilung ist in Abbildung 6 dargestellt.
Tabelle 6 Statistische Tabelle der relativen Abweichung von der Vickershärte zur Festigkeit
| Statistische Positionen | Minimaler Wert | Maximum | Durchschnittliche Abweichung | Standard-Referenz |
| Relative Abweichung des oberen Umrechnungswertes der Streckgrenze | -19.30 | +17.55 | ±5.75 | 7.09 |
| Relative Abweichung der umgerechneten Zugfestigkeit | -12.32 | +15.83 | ±4.88 | 5.44 |
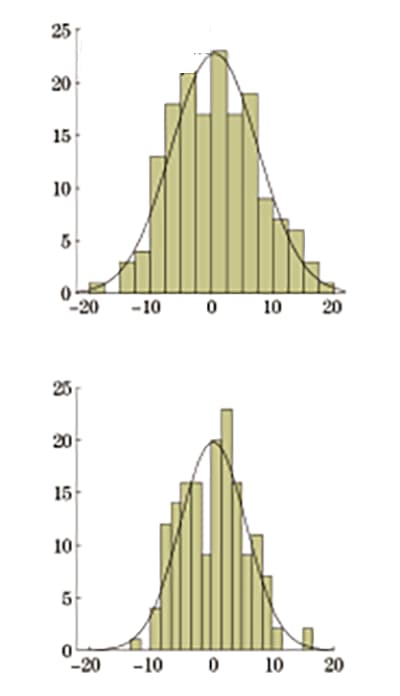
Abb. 6 Relative Abweichung der Vickershärte umgerechnet in Festigkeit
2.2.3 Vergleich mit dem nationalen Standardumrechnungswert
Abbildung 7 zeigt einen Vergleich des in der Norm angegebenen Umrechnungswerts der Zugfestigkeit, des Umrechnungswerts der vom Autor ermittelten linearen Regressionsformel und des Streudiagramms des entsprechenden Verhältnisses zwischen Vickershärte und Zugfestigkeit, alle auf demselben Diagramm.
Abb. 7 Vergleichstabelle der Zugfestigkeit umgerechnet in Vickershärte
Wie aus Abbildung 7 hervorgeht, ist der Gesamttrend der drei Kurven konsistent. Der in GB/T 1172-1999 angegebene Umrechnungswert der Zugfestigkeit kommt dem vom Autor ermittelten Umrechnungswert sehr nahe. Innerhalb des Bereichs von 370 bis 630 MPa nimmt die Differenz zwischen ihnen mit zunehmendem Härtewert leicht zu, wobei die durchschnittliche Abweichung 1,2% und die maximale Abweichung 3,3% beträgt. Der in GB/T 33362-2016 angegebene Umrechnungswert der Zugfestigkeit ist jedoch im Allgemeinen niedriger.
2.3.1 Brinell-Härte Testablauf und Ergebnisanalyse
Die Oberfläche der Probe wurde mit einer Schleifmaschine poliert, um eine Oberflächenrauhigkeit nicht größer als 1,6 μm. Das Gerät wurde mit einem Standard-Härteblock kalibriert, und die Brinell-Härteprüfung wurde gemäß den Anforderungen der GB/T 231.1-2018 Metallische Werkstoffe Brinell-Härteprüfung Teil 1: Prüfverfahren durchgeführt. A Sinterkarbid Eindringkörper mit einem Durchmesser von 10 mm verwendet, und die Prüfkraft betrug 29,42 kN. Für jede Probe wurden drei Punkte gemessen und der Durchschnittswert ermittelt.
Die SPSS-Software wurde verwendet, um eine lineare Regression, eine quadratische Regression, eine Potenzregression und eine exponentielle Regressionsanalyse für die Brinell-Härte, die obere Streckgrenze und die Zugfestigkeit durchzuführen. Das Diagramm der Regressionsanalyse ist in Abbildung 8 dargestellt, und die Ergebnisse der Regressionsanalyse sind in Tabelle 7 und Tabelle 8 aufgeführt.
Abb. 8 Regressionsanalyse von Brinellhärte und Festigkeit
Tabelle 7: Regressionsmodelldaten der Brinellhärte und der oberen Streckgrenze
| Gleichung | Modell Zusammenfassung | Modellparameter | ||||
| R2 | F | Signifikanz P | Konstante | b1 | b2 | |
| Linearer quadratischer Exponent | 0.756 | 495.403 | 0.000 | -59.965 | 2.846 | -0.001 |
| 0.758 | 246.186 | 0.000 | -86.188 | 3.205 | ||
| 0.757 | 497.365 | 0.000 | 1.048 | 1.168 | ||
| 0.756 | 494.881 | 0.000 | 110.318 | 0.008 | ||
Tabelle 8: Regressionsmodelldaten für Brinellhärte und Zugfestigkeit
| Gleichung | Modell Zusammenfassung | Modellparameter | ||||
| R2 | F | Signifikanz P | Konstante | b1 | b2 | |
| Linearer quadratischer Exponent | 0.887 | 1253.313 | 0.000 | -2.613 | 3.377 | -0.001 |
| 0.888 | 631.852 | 0.000 | -225.666 | 6.424 | ||
| 0.889 | 1286.205 | 0.000 | 3.204 | 1.009 | ||
| 0.886 | 1238.834 | 0.000 | 179.073 | 0.007 | ||
Wie aus Tabelle 7 und Tabelle 8 hervorgeht, korreliert die Brinellhärte stark mit der Festigkeit, und die Korrelation mit der Zugfestigkeit ist im Vergleich zur oberen Streckgrenze stärker.
Von den vier Regressionsmodellen zwischen Brinell-Härte und Festigkeit haben alle eine Signifikanz P kleiner als 0,05 und eine enge Anpassungsgüte R2.
Angesichts der Tatsache, dass die Umrechnungsbeziehung zwischen Kohlenstoffstahl Brinell-Härte und der in der Norm angegebenen Zugfestigkeit nahe an einer linearen Beziehung liegt, wird empfohlen, für die Umrechnung eine lineare Beziehung zu verwenden.
Die angepasste Formel lautet:
Wo: HBW ist die Brinell-Härte.
2.3.2 Analyse der relativen Abweichung der Umrechnungsergebnisse
Anhand des angepassten linearen Regressionsmodells werden die relativen Abweichungen zwischen den umgerechneten Werten der oberen Streckgrenze und der Zugfestigkeit und den Ergebnissen der Zugversuche berechnet und statistisch ausgewertet.
Die Statistik beträgt 162, und die Ergebnisse sind in Tabelle 9 dargestellt.
Die relativen Abweichungen sind im Wesentlichen normalverteilt, und die Häufigkeitsverteilung ist in Abb. 9 dargestellt.
Tabelle 9 Statistische Tabelle der relativen Abweichung von der Brinellhärte zur Festigkeit
| Statistische Positionen | Minimaler Wert | Maximum | Durchschnittliche Abweichung | Standard-Referenz |
| Relative Abweichung des oberen Umrechnungswertes der Streckgrenze | -16.78 | +18.67 | ±5.38 | 6.75 |
| Relative Abweichung der umgerechneten Zugfestigkeit | -9.25 | +8.55 | ±2.89 | 3.59 |
Abb. 9 Relative Abweichung der Brinellhärte umgerechnet in Festigkeit
2.3.3 Vergleich mit dem nationalen Standardumrechnungswert
In der Norm GB/T 1172-1999 beträgt das Verhältnis zwischen Prüfkraft und Durchmesser der Eindringkugel bei der Härteprüfung nach Brinell 10.
Die Prüfung des Autors wird nach GB/T 231.1-2018 durchgeführt. Unter Bezugnahme auf die Bestimmungen der Norm beträgt das Verhältnis der Prüfkraft zum Durchmesser der Eindringkugel 30.
Daher wird er nicht mehr mit GB/T 1172-1999 verglichen, wenn es um den Umrechnungswert der nationalen Norm geht.
Der in GB/T 33362-2016 angegebene Standard-Umrechnungswert der Zugfestigkeit, der Umrechnungswert der vom Autor angepassten linearen Regressionsformel und das Streudiagramm der entsprechenden Beziehung zwischen Brinell-Härte und Zugfestigkeit werden in derselben Tabelle verglichen, wie in Abb. 10 dargestellt.
Abb. 10 Vergleichstabelle der Zugfestigkeit umgerechnet in Brinellhärte
Aus Abb. 10 ist ersichtlich, dass der in GB/T 33362-2016 angegebene Umrechnungswert der Zugfestigkeit fast mit der vom Autor angepassten Regressionskurve der Zugfestigkeit übereinstimmt, mit einer durchschnittlichen Abweichung von 0,4% und einer maximalen Abweichung von 1,2% innerhalb von 370-630MPa.
In den letzten Jahren hat die rasche Entwicklung verschiedener tragbarer Härteprüfgeräte die Prüfung vor Ort sehr erleichtert.
Derzeit können viele Arten von tragbaren Rockwell-Härteprüfgeräten und tragbaren Brinell-Härteprüfgeräten auf dem Markt erworben werden.
Das Gerät ist tragbar, einfach zu bedienen, schnell zu messen, und die Nachweisgenauigkeit entspricht auch den Anforderungen der nationalen Normen, was für den Nachweis vor Ort geeignet ist.
Es gibt auch verschiedene tragbare Verarbeitungsgeräte für Proben Oberflächenbehandlungdie die Prüfanforderungen erfüllen können.
Daher ist es möglich, die Rockwell- und Brinellhärte zur Berechnung der Stahlfestigkeit bei der Vor-Ort-Prüfung von Stahlkonstruktionen zu verwenden.
| Härte | Zugfestigkeit σb/MPa | ||||||||||||||||
| Rockwell | Oberfläche Rockwell | Vickers | Brinell | Kohlenstoffstahl | Chromstahl | Chrom-Barium-Stahl | Chrom-Nickel-Stahl | Chrom-Molybdän-Stahl | Chrom-Nickel-Molybdän-Stahl | Chrom-Mangan-Silizium-Stahl | Ultrahochfester Stahl | Rostfreier Stahl | Keine spezifische Stahlsorte angegeben | ||||
| HRC | HRA | HR15N | HR30N | HR45N | HV | HB30D2 | d10、2d5、4d2.5 /mm | ||||||||||
| 17 | – | 67.3 | 37.9 | 15.6 | 211 | 211 | 4.15 | 73.6 | 706 | 705 | 772 | 726 | – | 757 | – | 703 | 724 |
| 18 | – | 67.8 | 38.9 | 16.8 | 216 | 216 | 4.11 | 753 | 723 | 719 | 779 | 737 | – | 769 | – | 719 | 737 |
| 19 | – | 68.3 | 39.8 | 18 | 221 | 220 | 4.07 | 771 | 739 | 735 | 788 | 749 | – | 782 | – | 737 | 752 |
| 20 | – | 68.8 | 40.7 | 19.2 | 226 | 225 | 4.03 | 790 | 757 | 751 | 797 | 761 | – | 796 | – | 754 | 767 |
| 21 | – | 69.3 | 41.7 | 20.4 | 231 | 227 | 4 | 809 | 775 | 767 | 807 | 775 | – | 810 | – | 773 | 782 |
| 22 | – | 69.8 | 42.6 | 21.5 | 237 | 234 | 3.95 | 829 | 794 | 785 | 819 | 789 | – | 825 | – | 792 | 799 |
| 23 | – | 70.3 | 43.6 | 22.7 | 243 | 240 | 3.91 | 849 | 814 | 803 | 831 | 805 | – | 840 | – | 812 | 816 |
| 24 | – | 70.8 | 44.5 | 23.9 | 249 | 245 | 3.87 | 870 | 834 | 823 | 845 | 821 | – | 856 | – | 832 | 835 |
| 25 | – | 71.4 | 45.5 | 25.1 | 255 | 251 | 3.83 | 892 | 855 | 843 | 860 | 838 | – | 874 | – | 853 | 854 |
| 26 | – | 71.9 | 46.4 | 26.3 | 261 | 257 | 3.78 | 914 | 876 | 864 | 876 | 857 | 876 | 892 | – | 875 | 874 |
| 27 | – | 72.4 | 47.3 | 27.5 | 268 | 263 | 3.74 | 937 | 898 | 886 | 893 | 877 | 897 | 910 | – | 897 | 895 |
| 28 | – | 73 | 48.3 | 28.7 | 274 | 269 | 3.7 | 961 | 920 | 909 | 912 | 897 | 918 | 930 | – | 919 | 917 |
| 29 | – | 73.5 | 49.2 | 29.9 | 281 | 276 | 3.65 | 984 | 943 | 933 | 932 | 919 | 941 | 951 | – | 942 | 940 |
| 30 | – | 74.1 | 50.2 | 31.1 | 289 | 283 | 3.61 | 1009 | 967 | 959 | 953 | 943 | 966 | 973 | – | 966 | 904 |
| 31 | – | 74.7 | 51.1 | 32.3 | 296 | 291 | 3.56 | 1034 | 991 | 985 | 976 | 967 | 991 | 996 | – | 990 | 989 |
| 32 | – | 75.2 | 52 | 33.5 | 304 | 298 | 3.52 | 1060 | 1016 | 1013 | 1001 | 993 | 1018 | 1020 | – | 1015 | 1015 |
| 33 | – | 75.8 | 53 | 34.7 | 312 | 306 | 3.48 | 1086 | 1042 | 1042 | 1027 | 1020 | 1047 | 1046 | – | 1041 | 1042 |
| 34 | – | 76.4 | 53.9 | 25.9 | 320 | 314 | 3.43 | 1113 | 1068 | 1072 | 1054 | 1049 | 1077 | 1073 | – | 1067 | 1070 |
| 35 | – | 77 | 54.8 | 37 | 329 | 323 | 3.39 | 1141 | 1095 | 1104 | 1084 | 1079 | 1108 | 1101 | – | 1095 | 1100 |
| 36 | – | 77.5 | 55.8 | 38.2 | 338 | 332 | 3.34 | 1170 | 1124 | 1136 | 1115 | 1111 | 1141 | 1130 | – | 1126 | 1131 |
| 37 | – | 78.1 | 56.7 | 39.4 | 347 | 341 | 3.3 | 1200 | 1153 | 1171 | 1148 | 1144 | 1176 | 1161 | – | 1153 | 1163 |
| 38 | – | 78.7 | 57.6 | 40.6 | 357 | 350 | 3.26 | 1231 | 1184 | 1206 | 1132 | 1179 | 1212 | 1194 | – | 1184 | 1197 |
| 39 | 70 | 79.3 | 58.6 | 41.8 | 367 | 360 | 3.21 | 1263 | 1216 | 1243 | 1219 | 1216 | 1250 | 1228 | 1218 | 1216 | 1232 |
| 40 | 70.5 | 79.9 | 59.5 | 43 | 377 | 370 | 3.17 | 1296 | 1249 | 1282 | 1257 | 1254 | 1290 | 1264 | 1267 | 1250 | 1268 |
| 41 | 71.1 | 80.5 | 60.4 | 44.2 | 388 | 380 | 3.13 | 1331 | 1284 | 1322 | 1298 | 1294 | 1331 | 1302 | 1315 | 1286 | 1307 |
| 42 | 71.6 | 81.1 | 61.3 | 45.4 | 399 | 391 | 3.09 | 1367 | 1322 | 1364 | 1340 | 1336 | 1375 | 1342 | 1362 | 1325 | 1347 |
| 43 | 72.1 | 81.7 | 62.3 | 46.5 | 411 | 401 | 3.05 | 1405 | 1361 | 1407 | 1385 | 1379 | 1420 | 1384 | 1409 | 1366 | 1389 |
| 44 | 72.6 | 82.3 | 63.2 | 47.7 | 423 | 413 | 3.01 | 1445 | 1403 | 1452 | 1431 | 1425 | 1467 | 1427 | 1455 | 1410 | 1434 |
| 45 | 73.2 | 82.9 | 64.1 | 48.9 | 436 | 424 | 2.97 | 1488 | 1448 | 1498 | 1480 | 1472 | 1516 | 1474 | 1502 | 1457 | 1480 |
| 46 | 73.7 | 83.5 | 65 | 50.1 | 449 | 436 | 2.93 | 1533 | 1497 | 1547 | 1531 | 1522 | 1567 | 1522 | 1550 | 1508 | 1529 |
| 47 | 74.2 | 84 | 65.9 | 51.2 | 462 | 449 | 2.89 | 1581 | 1549 | 1597 | 1584 | 1573 | 1620 | 1573 | 1600 | 1563 | 1581 |
| 48 | 74.7 | 84.6 | 66.8 | 52.4 | 478 | 401 | 2.85 | 1631 | 1605 | 1649 | 1640 | 1626 | 1676 | 1627 | 1652 | 1623 | 1635 |
| 49 | 75.3 | 85.2 | 67.7 | 53.6 | 493 | 474 | 2.81 | 1686 | 1666 | 1702 | 1698 | 1682 | 1733 | 1683 | 1707 | 1688 | 1692 |
| 50 | 75.8 | 85.7 | 68.6 | 54.7 | 509 | 488 | 2.77 | 1744 | 1731 | 1758 | 1758 | 1739 | 1793 | 1742 | 1765 | 1759 | 1753 |
| 51 | 76.3 | 86.3 | 69.5 | 55.9 | 525 | 501 | 2.73 | – | 1803 | 1816 | 1821 | 1799 | 1854 | 1804 | 1827 | – | 1817 |
| 52 | 76.9 | 86.8 | 70.4 | 57.1 | 543 | – | – | – | 1881 | 1875 | 1887 | 1861 | 1918 | 1870 | 1894 | – | 1885 |
| 53 | 77.4 | 87.4 | 71.3 | 58.2 | 561 | – | – | – | – | 1937 | 1955 | 1925 | 1985 | 1938 | 1967 | – | 1957 |
| 54 | 77.9 | 87.9 | 72.2 | 59.4 | 579 | – | – | – | – | 2000 | 2025 | – | – | 2010 | 2045 | – | 2034 |
| 55 | 78.5 | 88.4 | 73.1 | 60.5 | 599 | – | – | – | – | 2066 | 2098 | – | – | 2086 | 2131 | – | 2115 |
| 56 | 79 | 88.9 | 73.9 | 61.7 | 620 | – | – | – | – | – | – | – | – | – | 2224 | – | 2201 |
| 57 | 79.5 | 89.4 | 74.8 | 62.8 | 642 | – | – | – | – | – | – | – | – | – | 2324 | – | 2293 |
| 58 | 80.1 | 89.8 | 75.6 | 63.9 | 664 | – | – | – | – | – | – | – | – | – | 2437 | – | 2391 |
| 59 | 80.6 | 90.2 | 76.5 | 65.1 | 688 | – | – | – | – | – | – | – | – | – | 2558 | – | 2496 |
| 60 | 81.2 | 90.6 | 77.3 | 66.2 | 713 | – | – | – | – | – | – | – | – | – | 2691 | – | 2607 |
| 61 | 81.7 | 91 | 78.1 | 67.3 | 739 | – | – | – | – | – | – | – | – | – | – | – | – |
| 62 | 82.2 | 91.4 | 79 | 68.4 | 766 | – | – | – | – | – | – | – | – | – | – | – | – |
| 63 | 82.8 | 91.7 | 79.8 | 69.5 | 795 | – | – | – | – | – | – | – | – | – | – | – | – |
| 64 | 83.3 | 91.9 | 80.6 | 70.6 | 825 | – | – | – | – | – | – | – | – | – | – | – | – |
| 65 | 83.9 | 92.2 | 81.3 | 71.7 | 856 | – | – | – | – | – | – | – | – | – | – | – | – |
| 66 | 84.4 | – | – | – | 889 | – | – | – | – | – | – | – | – | – | – | – | – |
| 67 | 85 | – | – | – | 923 | – | – | – | – | – | – | – | – | – | – | – | – |
| 68 | 85.5 | – | – | – | 959 | – | – | – | – | – | – | – | – | – | – | – | – |
| 69 | 86.1 | – | – | – | 997 | – | – | – | – | – | – | – | – | – | – | – | – |
| 70 | 86.6 | – | – | – | 1037 | – | – | – | – | – | – | – | – | – | – | – | – |
(1) Rockwellhärte, Vickershärte und Brinellhärte zeigen eine gute Korrelation mit der Festigkeit. Auf der Grundlage von Materialtests wird die Umrechnungsformel von Rockwell-Härte, Vickers-Härte und Brinell-Härte und Festigkeit ermittelt, und die relative Abweichung der Umrechnung liegt innerhalb des zulässigen Bereichs des Projekts.
Die relative Abweichung zwischen Brinell-Härte und Zugfestigkeit ist deutlich geringer als die der Rockwell- und Vickers-Härte.
(2) Die in GB/T 33362-2016 angegebene umgewandelte Zugfestigkeit der Rockwell-Härte ist für Q235-Stahl niedrig und für Q345-Stahl hoch.
Die in Vickershärte umgerechnete Zugfestigkeit ist etwas geringer.
Die in Brinell-Härte umgerechnete Zugfestigkeit stimmt mit den Testergebnissen überein.
Die in GB/T 1172-1999 angegebenen Werte für die Zugfestigkeit, umgerechnet in Rockwell-Härte und Vickers-Härte, kommen den Testergebnissen sehr nahe.
(3) In Verbindung mit den vorhandenen tragbaren Härteprüfgeräten und Probenverarbeitungsanlagen ist die Verwendung der Rockwell- und Brinellhärte zur Berechnung der Festigkeit von Stahl in praktischen Projekten durchführbar und kann in der technischen Praxis angewendet werden.
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
AR 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO