Haben Sie sich jemals gefragt, wie die winzigen Nieten, die massive Strukturen zusammenhalten, eigentlich funktionieren? In diesem Artikel werden wir die faszinierende Welt der Nietverbindungen enträtseln und ihre Arten, Festigkeitsberechnungen und realen Anwendungen untersuchen. Am Ende werden Sie verstehen, welche entscheidende Rolle diese kleinen Komponenten in technischen Wunderwerken spielen. Bleiben Sie dran und erfahren Sie, wie Nieten unsere Welt sicher zusammenhalten!
Nietverbindungen sind ein grundlegendes Verfahren zum Verbinden von zwei oder mehr Werkstoffen, insbesondere von Metall, und werden in vielen Bereichen des Ingenieur- und Bauwesens eingesetzt. Nieten sind dauerhafte mechanische Verbindungselemente, die aus einem glatten zylindrischen Schaft mit einem Kopf an einem Ende bestehen. Bei der Montage wird der Niet in ein vorgebohrtes Loch eingeführt und dann das hintere Ende verformt, um einen zweiten Kopf zu erzeugen und so die Materialien miteinander zu verbinden.
In der Vergangenheit waren Nietverbindungen für den Bau bedeutender Bauwerke unerlässlich. Bemerkenswerte Beispiele sind der Eiffelturm in Paris und die Golden Gate Bridge in San Francisco. Diese Bauwerke zeugen von der Langlebigkeit und Stärke von Nietverbindungen, die sich im Laufe der Zeit bewährt haben und weiterhin zuverlässig funktionieren.
Die Anordnung der Nieten in Form von Ketten-, Zickzack- oder versetzten Mustern beeinflusst die Leistungsfähigkeit der Verbindung.
Nieten können aus verschiedenen Materialien hergestellt werden, darunter Aluminium, Stahl, Messing und Kupfer. Die Wahl des Materials hängt von spezifischen Anforderungen wie Festigkeit, Korrosionsbeständigkeit und Verformbarkeit ab.
Nietverbindungen werden bevorzugt dort eingesetzt, wo die Verbindung dynamischen Belastungen standhalten muss und wo unterschiedliche Materialien miteinander verbunden werden müssen. Sie werden auch wegen ihrer historischen Bedeutung und bewährten Zuverlässigkeit in kritischen Strukturen gewählt.
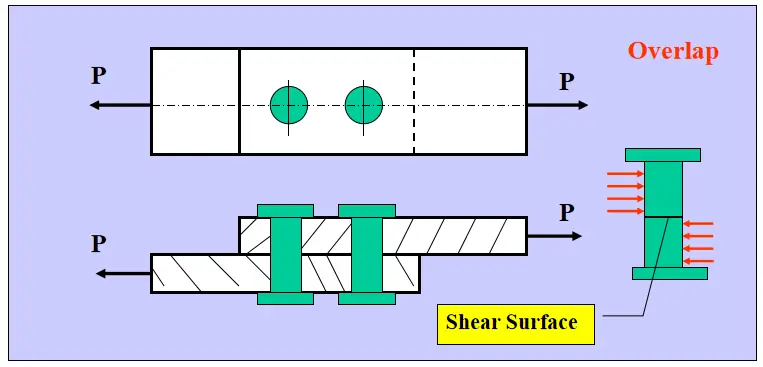
Einfacher Deckel Stumpfstoß
Doppelt abgedeckte Stoßfuge
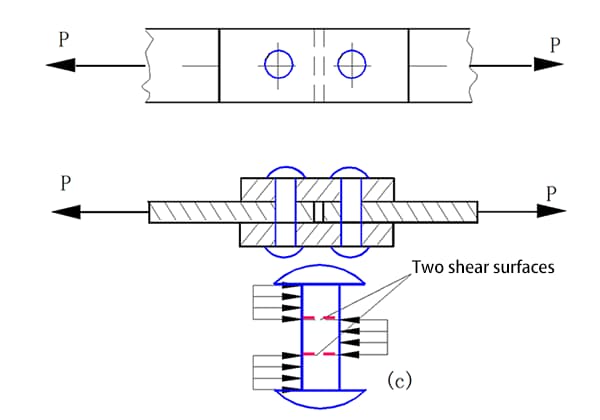
Seitliche Lastaufnahme der Nietgruppe
Bei einer Nietverbindung (wie in der obigen Abbildung dargestellt) wird zur Vereinfachung der Berechnungen angenommen, dass:
Die Formel zur Berechnung der auf jeden Niet wirkenden Kraft lautet:
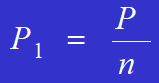
Beispiel:
Eine Verbindung mit vier Nieten wird verwendet, um zwei Stahlplatten zu verbinden. Das Material der Stahlplatten und der Nieten ist gleich. Der Durchmesser der Nieten beträgt d=16mm, die Größe der Stahlplatte ist b=100mm, t=10mm, P=90KN, die zulässige Spannung der Nieten ist [τ]=120MPa, die zulässige Streckspannung ist [σjy]=120MPa, und die zulässige Zugspannung des Stahlblechs beträgt [σ]=160MPa. Berechnen und prüfen Sie die Festigkeit der Nietverbindung.
(1) Scherfestigkeit der Nieten:
Die auf jeden Niet wirkende Kraft ist P/4.
Die auf jeden Niet wirkende Querkraft ist gegeben durch:
(2) Druckfestigkeit der Nieten:
Die auf jeden Niet wirkende Kraft aufgrund der Quetschung beträgt:
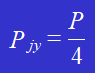
Der Bereich des Nietes, der gequetscht wird, ist:
(3) Zugfestigkeit der Stahlplatte
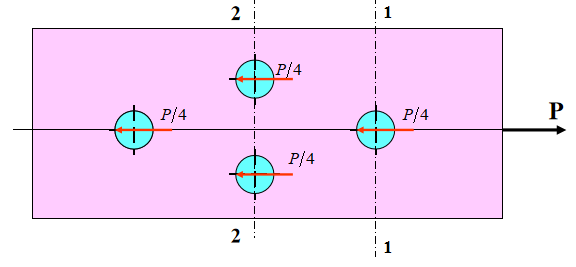
Eine Frage zum Nachdenken:
Fläche der Scherfläche für den Dübelstift A.
Fläche der Extrusionsfläche für den Dübelstift Ajy.
Zusätzliche Frage:
Stanzen Sie ein Loch mit der in der Abbildung gezeigten Form in eine 5 mm dick Stahlplatte. Wenn die Scherfestigkeitsgrenze des Stahlblechmaterials 𝜏 ist𝑏 = 300MPa, berechnen Sie die Stanzkraft F, die für die Stanzmaschine.
Lösung: Die Fläche der Scherfläche ist
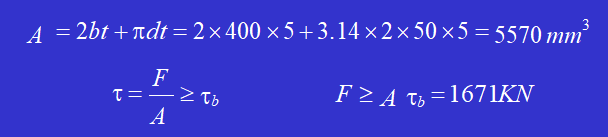
Zusätzliche Frage:
Die maximale Stanzkraft einer Stanzmaschine ist P = 400KN, die zulässige Druckspannung [𝜎] des Stanzmaterial beträgt 440MPa, und die Scherfestigkeit des Stahlblechs ist 𝜏𝑏 = 360MPa. Bestimmen Sie den minimalen Durchmesser d, den der Stempel stanzen kann, und die maximale Dicke 𝜹 des Stahlblechs, das gestanzt werden kann.
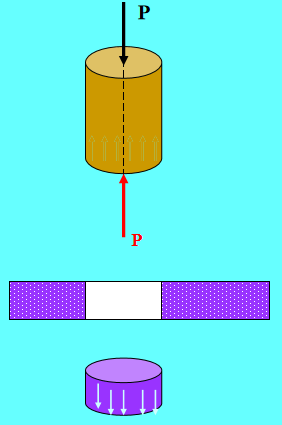
Lösung: Der Stempel erfährt eine axiale Druckverformung.
Entsprechend dem Scherbruchzustand der Stahlplatte:
Beispiel:
In Abbildung a und b ist die Situation der Verbindung zweier Stahlschienen mit einem Verbundträger dargestellt.
Die Querschnittsfläche jeder Stahlschiene A beträgt 8000 mm, und das Trägheitsmoment der Querschnittsfläche jeder Stahlschiene in Bezug auf ihren eigenen Schwerpunkt beträgt I = 1600 × 10 mm. Der Nietabstand s beträgt 150 mm, der Durchmesser d = 20 mm, und die zulässige Schubspannung [τ] beträgt 95 MPa. Wenn die innere Querkraft Q des Trägers 50 kN beträgt, ist die Scherfestigkeit der Nieten zu überprüfen. Die Reibung zwischen den oberen und unteren Stahlschienen wird nicht berücksichtigt.
Lösung: Wenn sich die obere und die untere Stahlschiene als Ganzes biegen, steht die Querschnittsfläche der oberen Stahlschiene unter Druckspannung und die Querschnittsfläche der unteren Stahlschiene unter Zugspannung.
Aufgrund der unterschiedlichen Biegemomente auf benachbarte Querschnitte sind die Normalspannungen an den entsprechenden Stellen unterschiedlich, so dass eine Tendenz zur Längsverschiebung entlang der Kontaktfläche zwischen den oberen und unteren Stahlschienen besteht, wodurch die Nieten Scherkräfte aufnehmen.
Die von jeder Nietreihe getragene Scherkraft ist gleich der Differenz der Druck- (Zug-) kraft auf zwei Querschnitte einer Stahlschiene im Längsabstand S.
Unter der Annahme, dass die Stahlschienen überall auf der Kontaktfläche Scherspannungen übertragen, ist die Breite der Kontaktfläche b.
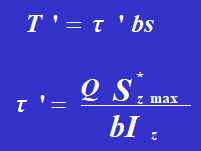
Szmax stellt das statische Moment der Querschnittsfläche einer Stahlschiene in Bezug auf die neutrale Achse dar.
Iz ist das Trägheitsmoment der gesamten Querschnittsfläche in Bezug auf die neutrale Achse.
Die Scherspannung des Nietes beträgt:
Die Scherspannung des Niets erfüllt die Festigkeitskriterien.
Nietverbindung, die einer Torsionsbelastung ausgesetzt ist (siehe Abbildung).
Der Schwerpunkt des Querschnitts der Nietanordnung sei der 0-Punkt.
Unter der Annahme, dass jede gerade Linie auf dem Stahlblech (wie OA oder OB) nach der Drehung gerade bleibt, ist die durchschnittliche Scherdehnung jedes Niets proportional zum Abstand von der Mitte des Nietquerschnitts zum Punkt O.
Wenn jeder Niet den gleichen Durchmesser hat, ist die auf jeden Niet wirkende Kraft proportional zum Abstand zwischen dem Mittelpunkt des Nietquerschnitts und dem Mittelpunkt O des Nietprofils, wobei die Richtung senkrecht zur Verbindungslinie zwischen dem Punkt und dem Mittelpunkt O verläuft.
Pi steht für die Kraft, die auf jeden Niet wirkt, und ai ist der Abstand von der Mitte des Querschnitts des betreffenden Nietes zum Schwerpunkt des Querschnitts der Nietanordnung, bezeichnet als O.
Die Nietbaugruppe, die exzentrischen seitlichen Belastungen ausgesetzt ist (siehe Abbildung a).
Vereinfacht man die exzentrische Last P, die auf die Nietbaugruppe wirkt, auf den Schwerpunkt O, so erhält man eine Kraft P, die durch den Punkt O verläuft, und ein Moment m = Pe die sich um den Punkt O dreht.
Wenn der Durchmesser jedes Niets in derselben Nietanordnung gleich ist, kann die durch die Querkraft P verursachte Kraft P1′ und die durch das Moment m verursachte Kraft P1" berechnet werden. Die auf jeden Niet wirkende Kraft ist die Vektorsumme aus P1′ und P1". Nach der Bestimmung der Kraft P1 auf jeden Niet kann die Scher- und Druckfestigkeit des Nietes mit der maximalen Kraft separat überprüft werden.
Beispiel:
Ein durch einen einzelnen Niet verbundener Bügel wird einer konzentrierten Kraft P ausgesetzt, wie in Abbildung a dargestellt. Die äußere Kraft P beträgt bekanntermaßen 12 kN. Der Niet hat einen Durchmesser von 20 mm, und jeder Niet wird auf einfache Scherung beansprucht. Berechnen Sie die maximale Scherspannung auf den Querschnitt des Niets unter der maximalen Kraft.
Lösung:
Die Nietanordnung ist symmetrisch zur x-Achse, und der Drehpunkt liegt im Punkt O, dem Schnittpunkt der Verbindungslinie zwischen Niet 2 und Niet 5 mit der x-Achse.
1. Vereinfacht man die Kraft P auf den Punkt O, so erhält man:
P = 12 kN.
m=12 0,12=1,44KN.m
2. Unter der Einwirkung der Kraft P, die durch den Drehpunkt geht, und unter der Annahme, dass jeder Niet den gleichen Durchmesser und das gleiche Material hat, ist die Kraft auf jeden Niet gleich.
3. Unter der Einwirkung des Moments m ist die Kraft, die jeder Niet trägt, proportional zum Abstand des Nietes vom Drehpunkt.
Nach der Bilanzgleichung:
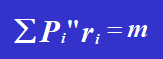
Lösen wir die Gleichung, erhalten wir:
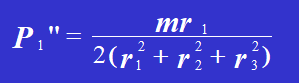
Deshalb,
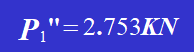
4. Zeichne das Kraftdiagramm jedes Niets und kombiniere die Vektoren Pi' und Pi", um die gesamte auf jeden Niet wirkende Scherkraft zu erhalten, einschließlich ihres Betrags und ihrer Richtung. Es kann festgestellt werden, dass Niet 1 und Niet 6 die größte Kraft tragen, wobei der Wert der maximalen Kraft beträgt:
Die Scherspannung im Querschnitt des Niets ist:
Nachstehend finden Sie Antworten auf einige häufig gestellte Fragen:
Im Bauwesen werden verschiedene Arten von Nieten aufgrund ihrer einzigartigen Eigenschaften und Anwendungen verwendet. Vollnieten, auch Rundnieten genannt, sind die gebräuchlichste und älteste Art und bestehen aus einem massiven Schaft und einem Kopf. Sie werden durch Verformung des Schafts mit einem Hammer oder einem Presswerkzeug angebracht und sind aufgrund ihrer hohen Festigkeit und Zuverlässigkeit weit verbreitet. Stahlnieten ähneln den Vollnieten, sind aber für hochbelastete Anwendungen im gewerblichen Bau, wie Brücken und Hochhäuser, konzipiert.
Blindnieten oder Popnieten sind röhrenförmige Nieten mit einem Dorn in der Mitte, die mit einem Nietgerät angebracht werden. Sie sind ideal für Anwendungen, bei denen der Zugang zur Rückseite der Verbindung eingeschränkt ist. Treibnieten benötigen ähnlich wie Blindnieten kein Spezialwerkzeug und werden mit einem Hammer eingeschlagen. Sie eignen sich für Anwendungen, bei denen die Löcher nicht die gesamte Platte oder den Block durchdringen.
Bündige Nieten oder Senknieten haben versenkte Köpfe und Löcher, so dass sie bündig mit der Oberfläche abschließen, was den Luftwiderstand verringert und eine glatte Oberfläche ergibt. Spreiznieten oder gegabelte Nieten haben scharfe Enden, die sich in entgegengesetzte Richtungen spreizen, wenn sie in ein Material getrieben werden. Sie sind ideal für die Verbindung weicher Materialien wie Holz, Kunststoff und Leder. Röhrennieten sind hohl mit einem Kopf an einem Ende und einem Ende am anderen. Sie erfordern weniger Kraftaufwand bei der Installation und werden bei Anwendungen verwendet, bei denen die zu befestigenden Materialien weich sind.
Nieten werden aus verschiedenen Materialien hergestellt, darunter Edelstahl, Stahl, Aluminium, Messing und Kupfer, die jeweils auf der Grundlage der spezifischen Anforderungen des Projekts ausgewählt werden. Diese Materialien bieten unterschiedliche Festigkeiten, Korrosionsbeständigkeiten und Gewichtseigenschaften, wodurch Nieten für eine Reihe von Bauanwendungen vielseitig einsetzbar sind.
Beim Vergleich von Niet- und Schweißverbindungen ergeben sich einige wichtige Unterschiede und Überlegungen. Schweißverbindungen bieten im Allgemeinen eine höhere Festigkeit und Tragfähigkeit als Nietverbindungen. Eine solide Schweißverbindung kann 100% der Festigkeit des Grundmaterials erreichen, während Nietverbindungen aufgrund der Verringerung der Querschnittsfläche durch die für die Nieten gebohrten Löcher eine geringere Festigkeit aufweisen.
In Bezug auf Konstruktion und Montage ist das Schweißen oft einfacher und schneller, da es keine vorgebohrten Löcher oder zusätzliche Teile wie Nieten erfordert. Beim Nieten hingegen müssen die Nieten gebohrt, befestigt und abgeflacht werden, was zeit- und arbeitsintensiver ist.
Die Leistung bei Vibrationen und Ermüdung unterscheidet sich zwischen den beiden Methoden. Nietverbindungen halten zyklischen Belastungen und Vibrationen besser stand, da die Verformung und Ausdehnung der Nieten die Verbindung im Laufe der Zeit verstärken kann. Geschweißte Verbindungen sind zwar stabil, können aber bei wiederholten Belastungszyklen anfälliger für Verschleiß sein.
In Bezug auf Werkstoffe und Kompatibilität ist das Nieten vielseitiger für das Verbinden unterschiedlicher Werkstoffe, da es keine Berücksichtigung der Schmelzpunkte erfordert. Das Schweißen hingegen erfordert Materialien mit kompatiblen Schmelzpunkten und thermischen Eigenschaften.
Aus ästhetischer Sicht können geschweißte Verbindungen nach der Nachbearbeitung eine glattere Oberfläche aufweisen, die im Vergleich zu den sichtbaren Nietköpfen von Nietverbindungen oft ansprechender ist.
Was die Wartung und Demontage betrifft, so sind Nietverbindungen einfacher zu demontieren und zu reparieren, da die Nieten ausgebohrt und ersetzt werden können. Geschweißte Verbindungen sind dauerhafter und müssen für die Demontage geschnitten und neu geschweißt werden, was zeit- und kostenaufwändiger ist.
Was das Gewicht und die strukturelle Integrität angeht, sind geschweißte Konstruktionen in der Regel leichter, da sie keine zusätzlichen Materialien wie Nieten und Bänder benötigen. Genietete Strukturen können aufgrund dieser zusätzlichen Komponenten schwerer sein.
Kosten und Effizienz spielen bei der Wahl zwischen den beiden Methoden ebenfalls eine Rolle. Nieten ist trotz der niedrigen Kosten für einzelne Nieten aufgrund der anfallenden Material-, Betriebs- und Arbeitskosten insgesamt teurer. Schweißen, insbesondere mit automatisierten Verfahren, kann kosteneffizienter und schneller sein.
Zusammenfassend lässt sich sagen, dass die Entscheidung zwischen Nieten und Schweißen von den spezifischen Anforderungen der Anwendung abhängt, einschließlich der erforderlichen Festigkeit, der Materialkompatibilität, ästhetischer Überlegungen und der Wartungsanforderungen. Schweißen bietet eine höhere Festigkeit, ein einfacheres Design und eine schnellere Produktion, kann aber zu thermischem Verzug führen und ist weniger flexibel bei der Demontage. Nieten bietet eine bessere Widerstandsfähigkeit gegen Vibrationen, eine einfachere Demontage und die Möglichkeit, unterschiedliche Materialien zu verbinden, ist aber im Allgemeinen schwächer und arbeitsintensiver.
Nietverbindungen werden in der modernen Technik aufgrund ihrer Langlebigkeit, Zuverlässigkeit und spezifischen Vorteile gegenüber anderen Verbindungsmethoden häufig eingesetzt. In der Luft- und Raumfahrtindustrie sind Nietverbindungen von entscheidender Bedeutung für die Verbindung von Bauteilen wie Rumpfplatten und Tragflächen, wo ihr geringes Gewicht und ihre hohe Festigkeit für die Aufrechterhaltung der strukturellen Integrität bei gleichzeitiger Gewichtsreduzierung von entscheidender Bedeutung sind. Im Schiffbau sind Nietverbindungen unverzichtbar für den Zusammenbau von Schiffsrümpfen und anderen wichtigen Teilen von Schiffen. Sie bieten Widerstand gegen Wasserdruck und Korrosion, was für die Gewährleistung der Wasserdichtigkeit und Sicherheit in rauen Gewässern entscheidend ist.
In der Bau- und Infrastrukturbranche werden Nietverbindungen in Konstruktionen wie Brücken, Türmen und Gebäuden eingesetzt. Diese Verbindungen werden für ihre Fähigkeit geschätzt, Lasten gleichmäßig zu verteilen und großen Strukturen Stabilität zu verleihen, was sie ideal für Anwendungen macht, die robuste Unterstützung erfordern, wie z. B. bei Brückenträgern und Fachwerken. Bei Druckbehältern und Kesseln werden Nietverbindungen bevorzugt, wenn thermische Verfahren wie Schweißen nicht praktikabel sind oder wenn die Verbindungen Temperaturschwankungen und Vibrationen standhalten müssen.
Auch die Automobilindustrie und der öffentliche Verkehr profitieren von Nietverbindungen, insbesondere bei der Herstellung von Bus- und Trolleybuskarosserien. Diese Verbindungen sorgen für starke und zuverlässige Verbindungen, die den Belastungen und Vibrationen in diesen Fahrzeugen standhalten. Darüber hinaus werden Nietverbindungen in Konsumgütern wie Küchenutensilien und Taschenmessern verwendet, wo ihre Festigkeit, ihr geringes Gewicht und ihre Korrosionsbeständigkeit von Vorteil sind.
Insgesamt werden Nietverbindungen in Umgebungen, die Vibrationen oder dynamischen Belastungen ausgesetzt sind, bevorzugt, da sie sich mit der Zeit nicht lockern. Sie eignen sich auch für Industrien mit Temperaturschwankungen, da sie keine Wärme für die Montage benötigen und resistent gegen Wärmeausdehnung sind. Außerdem sind Nietverbindungen im Vergleich zu Schweißverbindungen leichter zu prüfen und zu demontieren, wobei die betroffenen Teile weniger beschädigt werden. Diese Eigenschaften machen Nietverbindungen zu einer bevorzugten Methode in verschiedenen kritischen und leistungsstarken Industrien.
Nietverbindungen bieten eine Reihe von Vor- und Nachteilen, die sie für bestimmte Anwendungen geeignet machen, während sie in anderen Fällen eine Herausforderung darstellen.
Zu den Vorteilen von Nietverbindungen gehört die Kosteneffizienz, da Nieten kostengünstig sind und weder Strom noch spezielle Materialien benötigen, was sowohl Material- als auch Energiekosten spart. Nieten erhöht auch die Produktionsleistung, da es im Vergleich zum Schweißen in der Regel weniger Ausrüstung und Vorbereitung erfordert, wodurch Zeit und Ressourcen eingespart werden. Das Verfahren erzeugt nur minimale Abfallreste, was die Effizienz erhöht. Nietverbindungen bieten Flexibilität bei der Konstruktion und sind einfacher zu inspizieren und zu warten; abgenutzte Nieten können mit minimaler Ausrüstung schnell ersetzt werden. Sie sind vielseitig einsetzbar und können sowohl Eisen- und Nichteisenmetalle als auch nichtmetallische Materialien wie Holz, Kunststoff und Asbestplatten verbinden. Nieten ist umwelt- und benutzerfreundlich, da keine Dämpfe oder Gase entstehen, was es für die Arbeiter sicherer macht. Darüber hinaus bieten Nietverbindungen eine hohe Scherfestigkeit und eine gute Ermüdungsbeständigkeit und eignen sich daher für Anwendungen, die Vibrationen und Stoßkräften ausgesetzt sind.
Allerdings haben Nietverbindungen auch Nachteile. Sie erfordern einen höheren Arbeitsaufwand, da mehrere Schritte wie das Bohren von Löchern und das Anbringen der Nieten erforderlich sind, was die Personalkosten erhöhen kann. Nieten erhöhen das Gewicht der Struktur, was bei großen Strukturen erheblich sein kann und die Effizienz der Struktur beeinträchtigen kann. Die für die Nieten erforderlichen Löcher können die Metallplatten schwächen, was zu einer Spannungskonzentration um die Löcher herum führt und möglicherweise eine zusätzliche Dicke oder überlappende Platten erfordert, um die strukturelle Integrität zu erhalten. Aus ästhetischer Sicht sind genietete Verbindungen sichtbarer und können aus der Struktur herausragen, was den optischen Reiz im Vergleich zu geschweißten Verbindungen mindert. Nietverbindungen können bei der Montage Lärm verursachen und bei nicht ordnungsgemäßer Abdichtung korrosionsanfällig sein, was die Wartungskosten im Laufe der Zeit erhöht. Nietverbindungen bieten unter Umständen keine dichte oder leckdichte Abdichtung, es sei denn, es werden Heißnieten oder Dichtungsmittel verwendet, was bei bestimmten Anwendungen ein Nachteil sein kann. Schließlich können Nieten zwar ausgetauscht werden, aber der Vorgang kann mühsam und laut sein, und der Austausch von Nieten bei der Wartung kann im Vergleich zu anderen Befestigungsmethoden wie Schrauben schwieriger sein.
Zusammenfassend lässt sich sagen, dass Nietverbindungen kosteneffizient und flexibel sind, jedoch einen höheren Arbeitsaufwand, ein höheres Gewicht der Konstruktion, Probleme mit Spannungskonzentrationen und ästhetische Einschränkungen mit sich bringen. Die Wahl zwischen Nieten und anderen Verbindungsmethoden hängt von den spezifischen Projektanforderungen ab.
Die Instandhaltung und Reparatur von Nietverbindungen umfasst mehrere entscheidende Schritte, um die Integrität und Langlebigkeit der Struktur zu gewährleisten. Regelmäßige Inspektion ist der Schlüssel; überprüfen Sie Nietverbindungen auf Anzeichen von Verschleiß, Korrosion und Ermüdung. Reinigen Sie die Verbindungen regelmäßig, um Ablagerungen, Schmutz oder korrosive Substanzen zu entfernen, die die Verbindung beeinträchtigen könnten. Bei der Reinigung von pneumatischen Nietpistolen, die bei der Instandhaltung verwendet werden, ist auf eine gründliche Reinigung, Schmierung und Inspektion der Luftschläuche und Anschlüsse zu achten, um Fehlfunktionen zu vermeiden.
Bei Reparaturen sollten Sie zunächst alle Fehler wie falsche Nietgrößen oder eine unsachgemäße Lochvorbereitung feststellen. Wenn Nieten ersetzt werden müssen, entfernen Sie sie vorsichtig, indem Sie den Kopf durchbohren und den Schaft mit einem Splinttreiber abtrennen, ohne das umgebende Material zu beschädigen. Ersetzen Sie Nieten immer durch Nieten der richtigen Größe und des richtigen Typs und achten Sie auf die richtige Montagetechnik, um Probleme wie schräge Köpfe oder Risse zu vermeiden.
Für umfangreichere Reparaturen, vor allem bei älteren oder stark beschädigten Nieten, können spezielle Techniken wie Bobbing, Frenching und Ringschweißen eingesetzt werden. Außerdem ist es wichtig, potenzielle Korrosion durch ordnungsgemäßes Abdichten der Verbindungen zu bekämpfen, insbesondere wenn unterschiedliche Metalle beteiligt sind, um galvanische Korrosion zu verhindern.
Achten Sie darauf, dass Nietverbindungen keiner übermäßigen Ermüdung und Vibration ausgesetzt sind, die zu einem Versagen führen können. Vermeiden Sie eine zu starke Komprimierung während der Installation, um Hohlräume oder eine Kaltverfestigung des Metalls zu vermeiden. Führen Sie nach der Reparatur gründliche Tests und Inspektionen durch, um die strukturelle Integrität und Wasserdichtigkeit der Verbindungen zu bestätigen. Beheben Sie eventuelle Lecks umgehend durch zusätzliches Verstemmen oder Anpassen der Nieten.
Wenn Sie diese Wartungs- und Reparaturrichtlinien befolgen, können Sie die Festigkeit, Zuverlässigkeit und Sicherheit Ihrer Nietverbindungen auf Dauer erhalten.
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
AR 
ES 
FR 
ID 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR