Haben Sie sich jemals gefragt, was einen perfekten Kreis ausmacht? In der Welt des Maschinenbaus ist die Rundheit ein entscheidendes Konzept, das die Leistung und Langlebigkeit rotierender Bauteile beeinflusst. Dieser Artikel befasst sich mit den Feinheiten der Rundheit, ihrer Definition, den Messmethoden und den Faktoren, die sie beeinflussen. Ganz gleich, ob Sie ein erfahrener Ingenieur oder ein neugieriger Lernender sind, das Verständnis der Rundheit ist der Schlüssel zur Konstruktion und Wartung hochpräziser Maschinen.
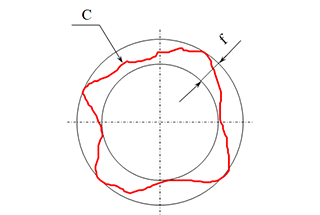
In der japanischen Industrienorm (JIS) B0621-1984, die sich auf die Definition und Angabe von Form- und Lageabweichungen bezieht, wird die Rundheit als "die Abweichung vom geometrischen Kreis eines kreisförmigen Körpers" definiert. Diese Norm bietet eine präzise Methode zur Darstellung der Rundheit, die für die Gewährleistung der Qualität und Funktionalität kreisförmiger Bauteile im Maschinenbau von entscheidender Bedeutung ist.
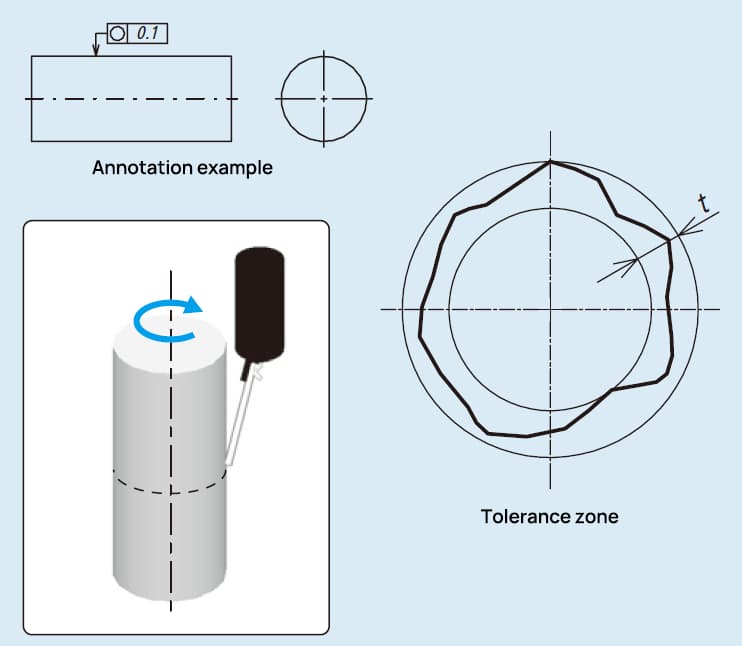
Die Darstellung der Rundheit in JIS B0621-1984 ist wie folgt:
Bei rotierenden Bauteilen ist die Bewertung ihrer echten Kreisform von entscheidender Bedeutung, um eine einwandfreie Funktion und Langlebigkeit zu gewährleisten. Das unmittelbare Anliegen ist die Bestimmung der Rundheitstoleranz, d. h. der zulässigen Abweichung von einem perfekten Kreis. Diese Bewertung beginnt mit:
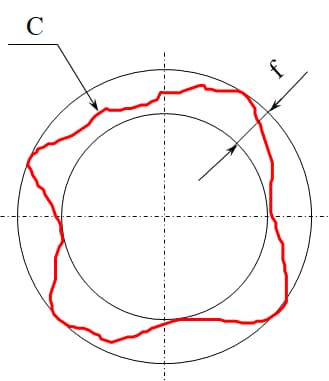
Die Rundheitstoleranz, auch Rundheitstoleranz genannt, ist eine Spezifikation für die geometrische Bemessung und Tolerierung (GD&T), die die zulässige Abweichung von einem perfekten Kreis in einer Querschnittsebene eines zylindrischen oder kugelförmigen Teils definiert. Sie stellt sicher, dass der gemessene Umfang eines Teils innerhalb einer festgelegten Toleranzzone liegt, die die Fläche zwischen zwei konzentrischen Kreisen desselben Querschnitts mit einer Radiusdifferenz von t ist. Diese Toleranzzone garantiert, dass das Teil innerhalb der festgelegten Grenzen eine gleichmäßige Kreisform beibehält.
Stellen Sie sich einen Querschnitt eines zylindrischen Teils vor. Das Toleranzfeld für die Rundheit wird als Fläche zwischen zwei konzentrischen Kreisen dargestellt. Die Radiusdifferenz t zwischen diesen Kreisen stellt die zulässige Abweichung von der idealen Kreisform dar. Jeder Punkt auf dem tatsächlichen Umfang des Teils muss innerhalb dieser Zone liegen, um die Anforderung an die Rundheitstoleranz zu erfüllen.
Verschiedene Faktoren können zu Abweichungen in der Rundheit und Zylindrizität führen, die die Präzision und Funktionalität der bearbeiteten Teile beeinträchtigen. Hier sind die häufigsten Ursachen:
Es gibt verschiedene Methoden zur Bewertung der Rundheit, die jeweils ihre eigenen Merkmale und Vorteile haben. Die Wahl der Methode richtet sich in der Regel nach den spezifischen Anforderungen des Werkstücks.
Zum Beispiel:
Durchmesser-Methode
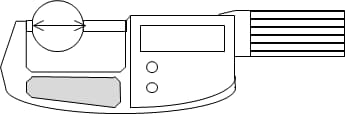
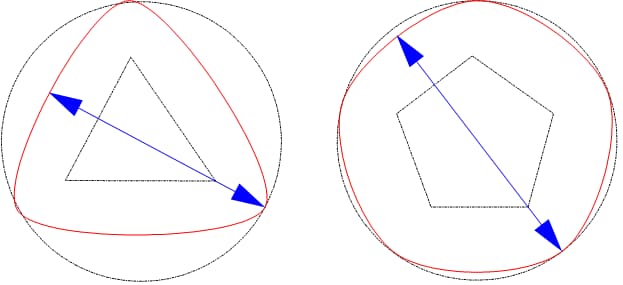
Die Rundheit kann direkt mit Werkzeugen wie Mikrometern gemessen werden. Diese Methode ist einfach und leicht durchzuführen. Bei der Bewertung von dreieckigen und fünfeckigen Kreisen mit gleichem Durchmesser ist es jedoch leicht möglich, sie als rund zu messen, wenn sie es nicht sind, was zu falschen Ergebnissen führt.
Drei-Punkte-Methode
Mit der Drei-Punkt-Methode können Rundheitsdaten durch [Prisma + Mikrometer / Messgerät + Prüfstand] ermittelt werden.
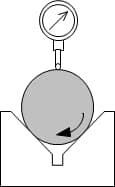
Die Drei-Punkt-Methode kann jedoch aufgrund von Unterschieden in der Tangente am gewählten Auflagepunkt und Schwierigkeiten bei der Bestimmung des Mittelpunkts des Referenzpunkts zu falschen Messungen führen. Darüber hinaus können während der Messung aufgrund der Auf- und Abwärtsbewegung bei der Drehung des zu messenden Objekts Fehler auftreten.
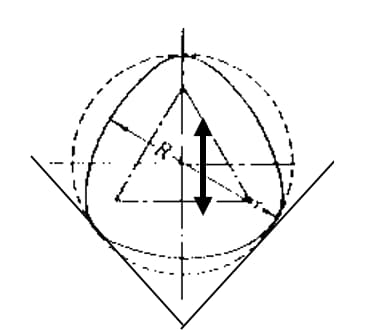
Zum Beispiel:
Radius-Methode
Bei der Radiusmethode wird die Rundheit anhand der Differenz zwischen dem maximalen und dem minimalen Radius bewertet, die nach einem Zyklus der Drehung des Werkstücks erzielt wird. Wie in der Abbildung zu sehen ist, können die Messergebnisse auch leicht durch den horizontalen Betrieb des Werkstücks beeinflusst werden.
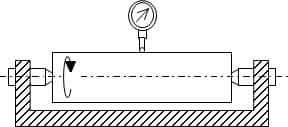
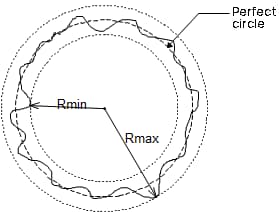
Die Toleranzzone liegt zwischen zwei konzentrischen Kreisen auf demselben Abschnitt
Zentrale Methode
Im Vergleich zur zentralen Methode wird die Radiusmethode meist für genauere Messungen verwendet. Die Daten der Rundheitserfassung hängen vom Referenzkreis ab. Unterschiedliche Bewertungsmethoden des Prüfkreises führen zu unterschiedlichen zentralen Positionen des Referenzkreises, was sich auf die axiale Position des gemessenen kreisförmigen Merkmals auswirkt.
Um die Rundheit zu bestimmen, wird die gemessene Kontur an einen Kreis angepasst und die Summe der Quadrate der Abweichung der Konturdaten vom Kreis minimiert. Anschließend wird der Rundheitswert als Differenz zwischen der maximalen Abweichung (höchster Spitzenwert bis niedrigster Talwert) der Kontur und des Kreises definiert.
ΔZｑ=Rmax-Rmin, Symbol für den Rundheitswert durch LSC
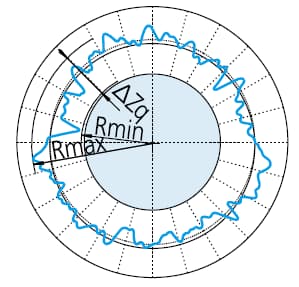
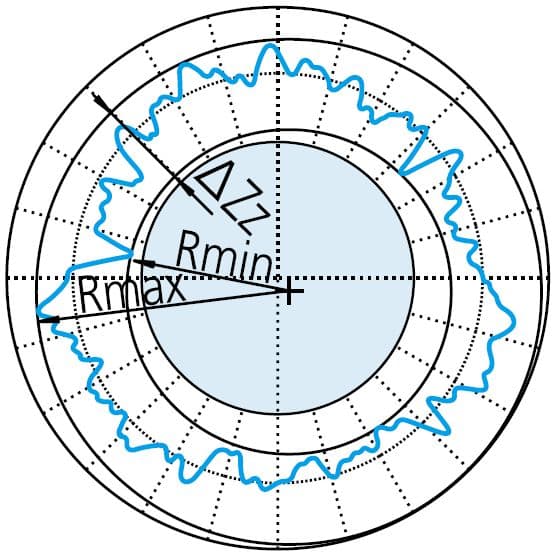
Um die radiale Differenz zu minimieren, werden zwei konzentrische Kreise um die gemessene Kontur gelegt. Der Rundheitswert ist definiert als der radiale Abstand zwischen den beiden Kreisen.
ΔZｚ=Rmax-Rmin , Symbol für den Rundheitswert durch MZC
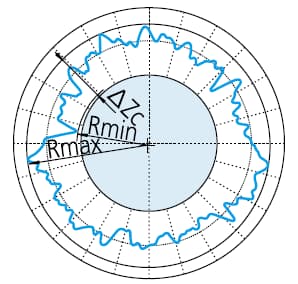
Zunächst wird der kleinste Kreis erstellt, der das gemessene Profil umschließt. Dann wird der Rundheitswert als maximale Abweichung zwischen der Kontur und dem Kreis definiert. Diese Methode wird üblicherweise zur Bewertung von Wellen, Stangen und ähnlichen Objekten verwendet.
ΔZｃ=Rmax-Rmin , das Symbol für den Rundheitswert durch MCC.
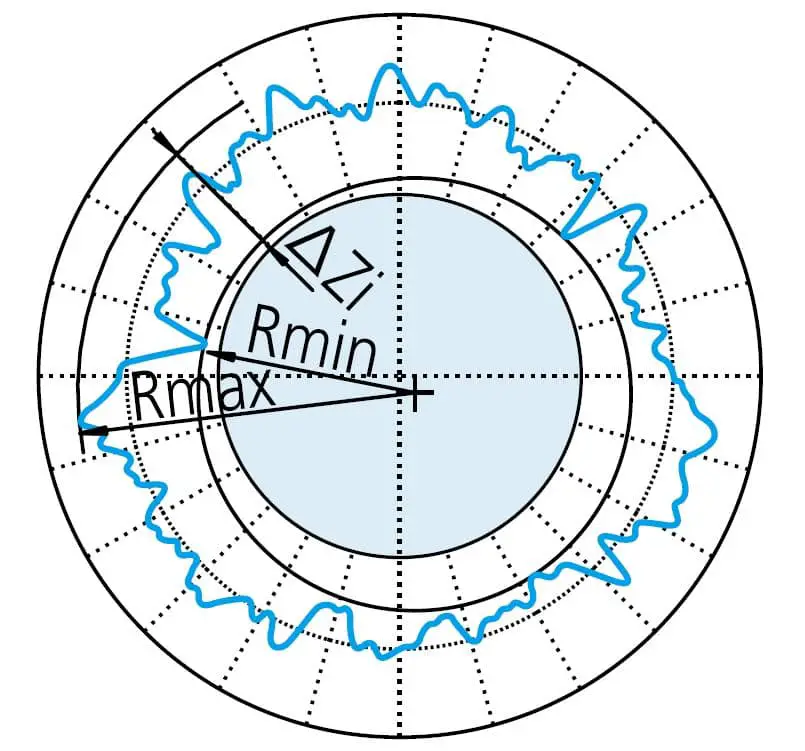
Erstellen Sie den größten Kreis, der das gemessene Profil umschließen kann. Dann wird der Rundheitswert als die maximale Abweichung zwischen der Kontur und dem Kreis definiert.
ΔZｉ=Rmax-Rmin , das Symbol, das den Rundheitswert durch MIC angibt.
Bei der Bewertung der Rundheit wird die erhaltene Kontur in der Regel gefiltert, um den Einfluss von unnötigem Rauschen zu reduzieren oder zu eliminieren.
Die Filterungsmethoden und die eingestellten Filtergrenzwerte (UPR: Schwankungen pro Umdrehung) können je nach den spezifischen Messanforderungen variieren. Die folgende Abbildung zeigt die unterschiedlichen Auswirkungen von Filtereinstellungen auf die gemessene Kontur.
Kein Filter:
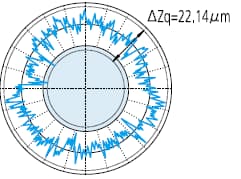
Tiefpassfilter:
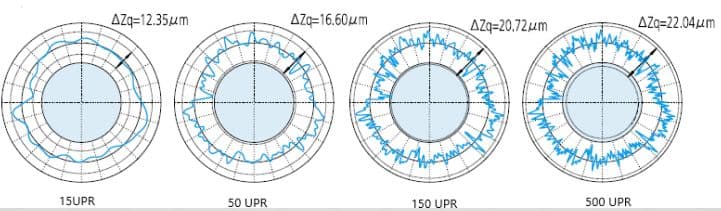
Bandpassfilter:
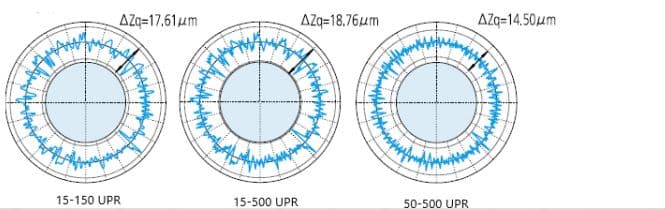
Was können uns als Bewerter diese Zahlen sagen?
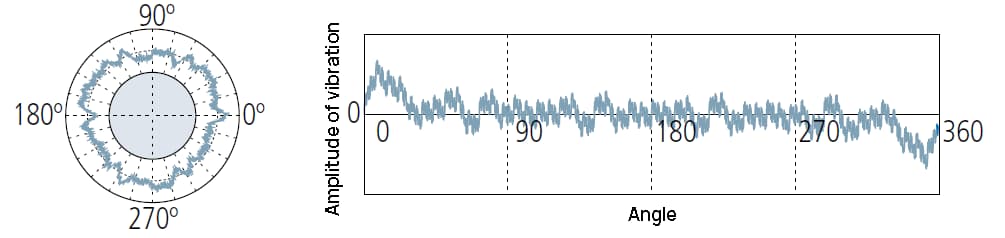
Abbildung: Diagramm der Messergebnisse
1 UPR: nur eine Welle wird nach der Filterung beibehalten:
1UPR-Komponente gibt die Exzentrizität des Werkstücks in Bezug auf die Drehachse des Messgeräts an.
Die Amplitude der Wellenform hängt von der Einstellung des Pegels ab.
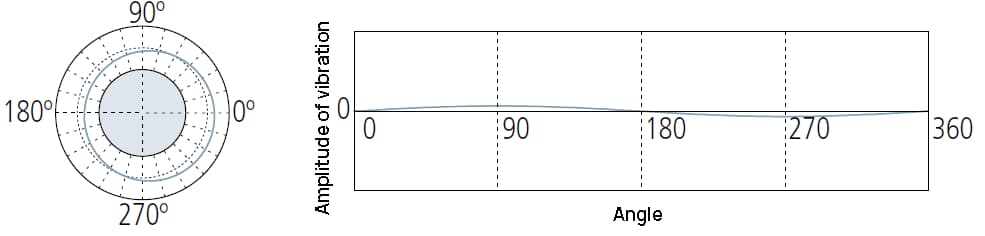
2UPR-Komponenten anzeigen können:
① Unzureichende Pegelanpassung der Messgeräte;
② Rundlauffehler, verursacht durch eine falsche Montage des Werkstücks auf der formgebenden Werkzeugmaschine;
③ Die Form des Werkstücks ist oval, z. B. bei einem Kolben eines Verbrennungsmotors.
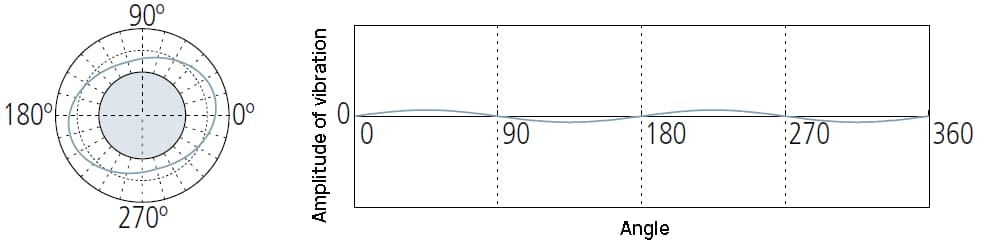
Kann anzeigen:
① Verformung durch zu festes Spannfutter am Messgerät.
② Relaxationsverformung durch Spannungsabbau beim Entladen aus dem festen Spannfutter der bearbeitenden Werkzeugmaschine.
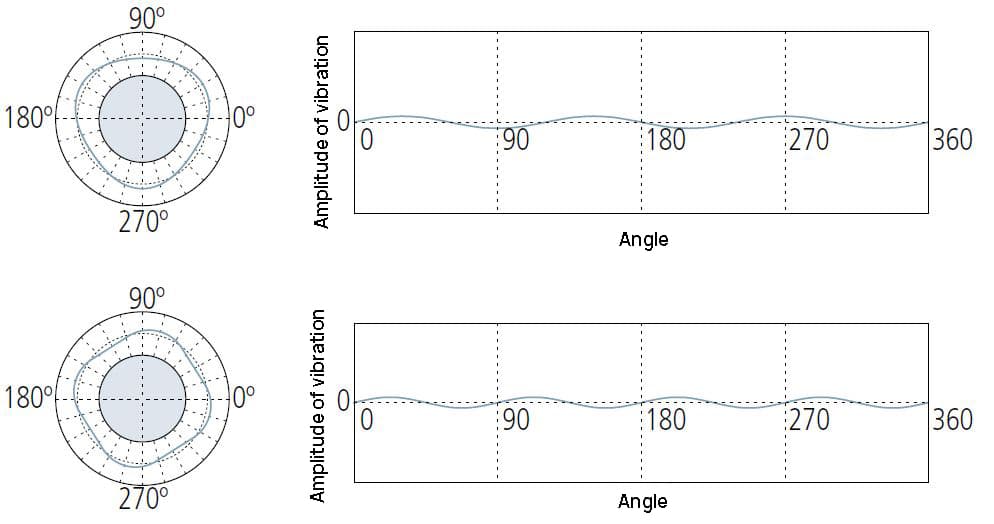
Er bezieht sich in der Regel auf unausgewogene Faktoren in der Bearbeitungsmethode oder im Prozess der Werkstückherstellung.
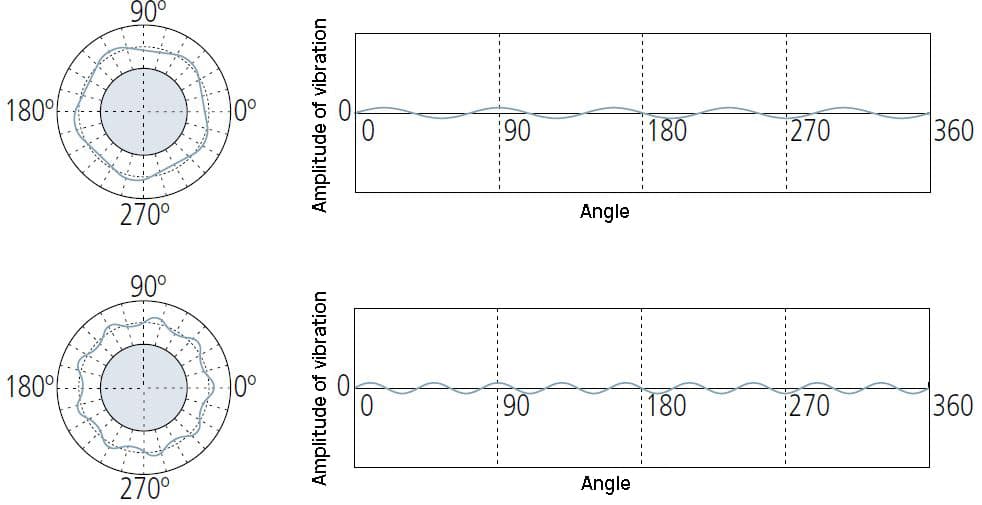
15 (oder mehr) UPR-Zustände sind in der Regel auf eigene Ursachen zurückzuführen, wie z. B. Werkzeugrattern, Maschinenvibrationen, Kühlmittelübertragungseffekte, Materialinhomogenität usw.
| Parameter | Bedeutung |
| RONt | Der Messwert der Rundheit ist die Differenz zwischen dem Maximalwert der positiven Rundheitskurve und dem Minimalwert der negativen Rundheitskurve oder die Summe der Absolutwerte. |
| RONp | Die gemessene Spitzenhöhe der Rundheitskurve stellt den Maximalwert der positiven Rundheitskurve dar. |
| RONV | Der gemessene Wert der Rundheit entspricht dem Absolutwert des Minimalwertes der negativen Rundheitskurve. |
| RONq | Der doppelte quadratische Mittelwert der Rundheitskurve stellt den doppelten quadratischen Mittelwert der Rundheitskurve dar. |
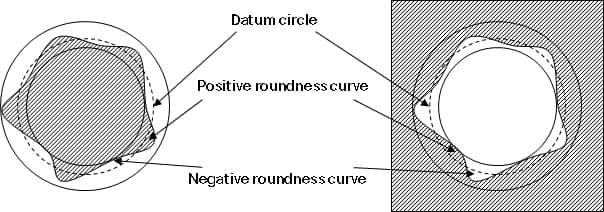
Abschließend wollen wir uns ansehen, welche Werkzeuge und Instrumente zur Messung der Rundheit zur Verfügung stehen.
Mikrometer:
Messgerät für die Rundheit:
Koordinatenmessmaschine:
Der Platz ist begrenzt, und Sie können gerne eine Nachricht hinterlassen und Kritik zu den nicht behandelten Themen äußern.
Ich hoffe, dass Sie nach der Lektüre dieses Artikels ein tieferes Verständnis von Rundheit gewonnen haben. Wenn Sie weitere Fragen haben, können Sie gerne unten einen Kommentar hinterlassen.
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
AR 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO