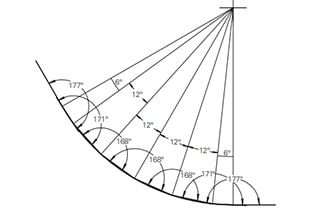
Hatten Sie schon einmal Probleme mit der genauen Abwicklung von Blechteilen? In diesem Artikel werden die Kunst und die Wissenschaft hinter der Berechnung von Blechabwicklungen untersucht. Entdecken Sie die wichtigsten Konzepte, Formeln und Techniken, die von erfahrenen Ingenieuren verwendet werden, um komplexe Geometrien präzise abzuwickeln. Erfahren Sie, wie Sie diese Prinzipien auf Ihre eigenen Konstruktionen anwenden und Ihren Fertigungsprozess rationalisieren können.
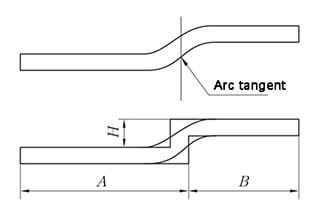
Der erste Schritt im Blechbearbeitungsprozess ist die Entfaltung der Geometrien und des kohärenten Körpers. Die Genauigkeit und Korrektheit der Musterentfaltung wirkt sich direkt auf die Qualität des endgültigen Teils aus.
In der Vergangenheit hat man aufgrund der begrenzten Möglichkeiten von Berechnungswerkzeugen die Projektionsmethode angewandt, um die Probe auf einer Ebene im Verhältnis 1:1 zu vergrößern und die tatsächliche Länge der erforderlichen Planlinie zu messen.
Diese Methode ist jedoch kompliziert und ineffizient und wird den heutigen Anforderungen der Produktion nicht gerecht.
Mit den Fortschritten bei den Berechnungsinstrumenten, wie z. B. elektronischen Taschenrechnern und dem weit verbreiteten Einsatz von Computern, Feinblech Die Entfaltung kann nun mit Berechnungsmethoden durchgeführt werden.
Um die Berechnungsmethode des Blechabwicklungskoeffizienten durch die Techniker zu standardisieren, die Maßabweichungen der Produkte nach dem Biegen zu minimieren und die Selbstinspektion durch das Werkstattpersonal und die erneute Inspektion durch Qualitätsprüfer zu erleichtern, gibt es eine einheitliche Norm und Grundlage für den Abwicklungskoeffizienten.
Infolgedessen hat sich der Berechnungsstandard für den Blechabwicklungskoeffizienten zunehmend vereinheitlicht.
Neutralschicht-Entfaltungsmethode
Bei der Biegung wird die äußere Schicht auf Zug beansprucht, während die innere Schicht auf Druck beansprucht wird. Die Übergangsschicht zwischen Zug- und Druckspannung wird als neutrale Schicht bezeichnet. Die Länge der neutralen Schicht bleibt während des Biegens gleich wie vor dem Biegen und ist somit der Maßstab für die Bestimmung der entfalteten Länge des Biegeteils.
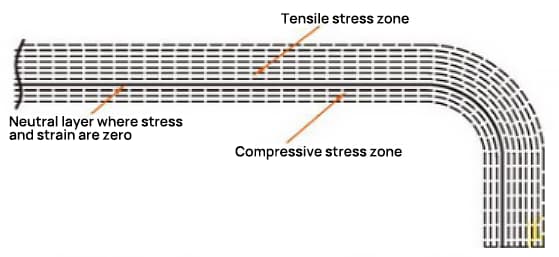
Die Lage der neutralen Schicht ist abhängig vom Grad der Verformung.
Die Position der neutralen Schicht hängt nicht nur vom Biegeradius, der Blechdicke, dem Einwärtsverschiebungskoeffizienten usw. ab, sondern auch von Faktoren wie dem Verarbeitungsverfahren, der Blechform und der Größe.
Daher kann die Lage der neutralen Schicht nur annähernd bestimmt werden, und in der Praxis werden in der Regel Näherungswerte für die Berechnung verwendet.
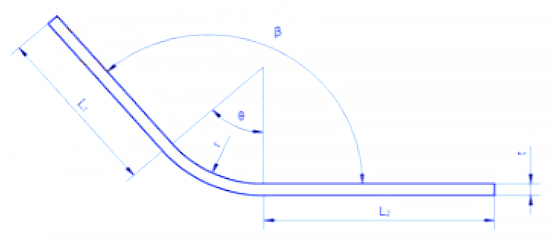
Die Berechnungsformel für das Längenmaß L der neutralen Schicht lautet:
Darunter,
Durch den Einsatz von 3D-Software zur Durchführung von Simulationen und Berechnungen verschiedener Dicken, Winkel und Radien sowie der Fertigungspraktiken vor Ort haben wir eine Reihe von K-Faktor-Werten zusammengestellt. Die spezifischen Werte finden Sie in Tabelle 1.
Tabelle 1: Neutralschichtkoeffizient K-Werte
| r/t | ≤05 | 0.6 | 0.8 | 1 | 1.2 | 1.3 | 1.5 | 2 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | ≥8 |
| k | 026 | 0.28 | 0.30 | 0.32 | 0.33 | 0.34 | 0.36 | 0.38 | 0.39 | 0.4 | 0.42 | 0.44 | 0.46 | 0.5 |
Schnellabwicklungsberechnung für 90°-Bögen
Das Abwicklungsdiagramm für eine 90°-Biegung ist in Abbildung 9 dargestellt. In den letzten Jahren haben wir 3D-Software wie CATIA und SOLIDWORKS für die Blechmodellierung verwendet, um die Abwicklungsmaße zu berechnen.
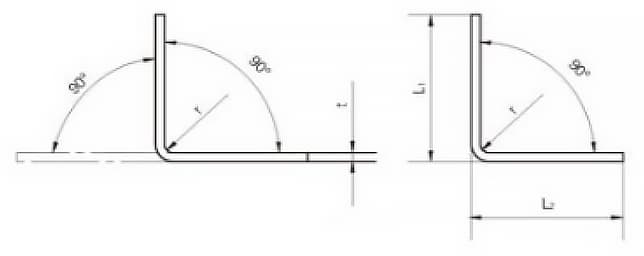
Durch wiederholte Überprüfung wurde festgestellt, dass bei einem Kaltbiegewinkel von 90° bei Flachstahlprodukten die Formel für die Berechnung der entfalteten Länge L lautet:
L = L1 + L2 - A
Wo,
Tabelle 2 90 ° Biegeparameter Tabelle
| Dicke t/mm | Bedingungsradius r/mm | |||||||||||
| 1 | 1.2 | 16 | 2 | 25 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | |
| Ausgleichswert A mm | ||||||||||||
| 1 | -1.92 | -1.97 | -2.10 | -2.23 | -2.41 | -2.59 | -2.97 | -3.36 | -3.79 | -4.65 | -5.51 | -6.37 |
| 1.5 | -2.90 | -3.02 | -3.18 | -3.34 | -3.70 | -4.07 | -4.45 | -5.26 | -6.11 | -6.97 | ||
| 2 | -3.84 | -3.98 | -4.13 | -4.46 | -4.81 | -5.18 | -5.94 | -6.72 | -7.58 | |||
| 2.5 | -4.80 | -4.93 | -5.24 | -5.57 | -5.93 | -6.66 | -7.42 | -8.21 | ||||
| 3 | -5.76 | 6.04 | -6.35 | -6.69 | -7.40 | -8.14 | -8.91 | |||||
| 4 | -7.7 | -7.95 | -8.26 | -8.92 | -9.62 | -10.36 | ||||||
| 5 | -9.6 | -9.87 | -10.48 | -11.15 | -11.85 | |||||||
| 6 | -11.5 | -12.08 | -12.71 | -13.38 | ||||||||
| 8 | -15.4 | -15.9 | -16.51 | |||||||||
| 10 | -19.2 | -19.73 | ||||||||||
| 12 | 23.01 | |||||||||||
Wenn die Biegeradius groß und der Biegewinkel klein ist, ist der Grad der Verformung gering und die neutrale Schicht liegt nahe der Mitte der Blechdicke.
Wenn jedoch der Biegeradius (R) kleiner wird und die Biegewinkel (θ) zunimmt, nimmt auch der Grad der Verformung zu, und die neutrale Schicht bewegt sich in Richtung der Innenseite des Biegezentrums. Der Abstand zwischen der neutralen Schicht und der Innenseite des Blechs wird mit λ und die Materialdicke mit T bezeichnet.
Die Grundformel für die Berechnung der Entfaltungslänge:
Entfaltungslänge = innere Größe des Materials + innere Größe des Materials + Ausgleichsbetrag.
Sie können auch den folgenden Rechner verwenden, um die Abwicklungslänge von Blechen zu berechnen:

Im Folgenden werden die Entfaltungsalgorithmen der verschiedenen Biegemerkmale einzeln beschrieben.
R = 0mm, θ = 90° (Anmerkung: Wenn R ≤ 1,0mm ist, wird es als R = 0mm behandelt).
L = A + B + K
In der tatsächlichen Produktion kann die obere Biegematrize einen R-Winkel aufweisen, oder es kann ein R-Winkel von weniger als 1 mm vorhanden sein, oder die Wahl des UntergesenkDie V-Nut der Platte kann unter anderem groß sein, was zu einem kleinen Biegekoeffizienten führt. Daher wird der Biegekoeffizient für jede Materialplattendicke in Tabelle 1 auf der Grundlage tatsächlicher empirischer Werte angegeben.
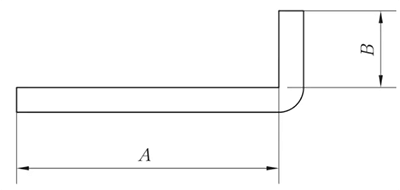
Abb. 1 Schematische Darstellung der allgemeinen Biegung I
R ≠ 0mm und θ = 90°
L = A + B + K (K ist die Bogenlänge der neutralen Schicht)
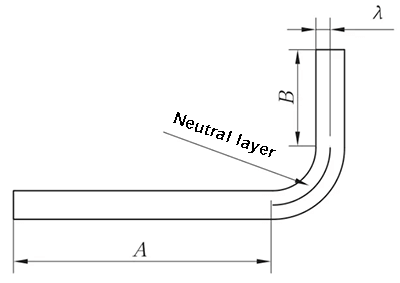
Abb. 2 Schematische Darstellung der allgemeinen Biegung II
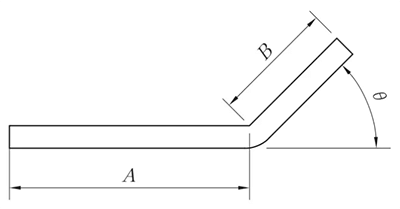
R = 0mm, θ ≠ 90°
L = A + B + K'
Anmerkung: K ist der Ausgleichsbetrag bei 90°.
R ≠ 0mm, θ ≠ 90°
L = A + B + K
(K ist die Bogenlänge der neutralen Schicht)
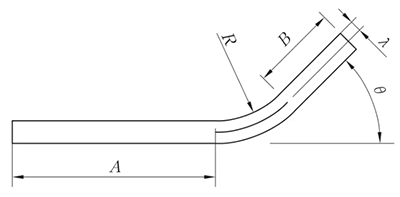
Abb. 4 Allgemeines Biegen IV Biegediagramm
Die Methode der Entfaltung entspricht der Methode der parallelen, kantengeraden Z-Faltung, und die Messung der Höhe ist in Abbildung 6 dargestellt.
Der Winkel θ wird als eine 90°-Abwicklung betrachtet.
Für 0 < T ≤ 1,6 mm ist λ gleich 0,5 T.
Wenn T größer als 1,6 mm ist, ist λ gleich 0,4 T.
Z-Fold, auch bezeichnet als Gekröpftes Biegenwird anhand des Umformwinkels in Geradkantenversatzbiegen und Schrägkantenversatzbiegen unterschieden, und die Art der Bearbeitung wird durch die Versatzhöhe bestimmt.
Wenn die Versatzhöhe h weniger als das 3,5-fache der Materialdicke beträgt, Offsetdruckstempel oder auswechselbare Matrizen werden für die Umformung verwendet.
Übersteigt die Versatzhöhe das 3,5-fache der Materialdicke, erfolgt eine normale Positiv- und Negativumformung.
Wenn die Länge der abgeschrägten Kante weniger als das 3,5-fache der Materialdicke beträgt, werden für die Umformung versetzte Werkzeuge oder auswechselbare Werkzeuge verwendet.
Überschreitet die Länge der abgeschrägten Kante das 3,5-fache der Materialdicke, wird die normale Faltung mit einem positiven und einem negativen Wert durchgeführt.
(1) Wenn H < 3,5 T, nur dann kann durch Offset-Biegen verarbeitet werden.
L = A + B + H
(wenn H ≤ T, dann 0,2 mm ausgleichen)
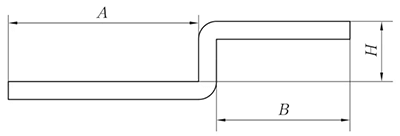
Abb. 5 Schematische Darstellung des Kantenversatzes
(2) Nicht-paralleles Kantenlineal versetzt
Die Expansionsmethode ist die gleiche wie die Methode der parallelen Z-Faltung mit geradem Rand, und der Höhenwert ist in Abbildung 6 dargestellt.
Der Winkel θ kann als 90 ° aufgefaltet betrachtet werden.
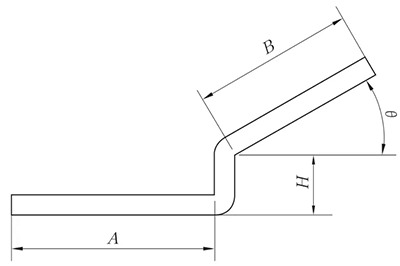
Abb. 6 Schematische Darstellung des nicht-parallelen Kantenversatzes
(3) Gerader Kantenversatz - das Übergangssegment ist tangential zu zwei Bögen
Wenn der Straight-Edge-Offset am Tangentenpunkt zweier Kreisbögen entfaltet wird, entsteht eine vertikale Linie am Tangentenpunkt der beiden Kreisbögen auf der Außenfläche des Substrats. Das Material wird dann zur Verarbeitung um eine Materialdicke nach innen versetzt, wie in Abbildung 7 dargestellt, und mit der Methode Z-Fold 1 (Straight-Edge Offset) entfaltet.
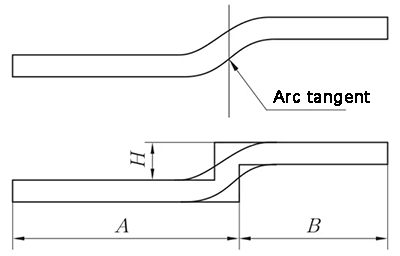
Abb. 7 Diagramm der geraden Kantenverschiebung - Übergangssegment tangiert zwei Kreisbögen
Wenn H < 2T, ist der Entfaltungsalgorithmus entsprechend der Offset-Verarbeitung wie folgt.
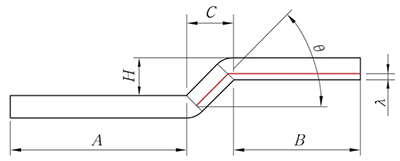
Abb. 8 Diagramm der abgeschrägten Kantenversetzung
L = A + B - K
(1) Beim Abflachen sollte die Leitung vor dem Biegen unter Berücksichtigung der tatsächlichen Bedingungen gepresst werden.
Der Ort der Linienpressung liegt in der Mitte des Biegeverformungsbereichs.
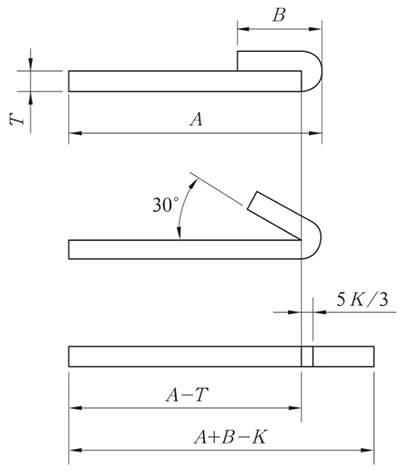
Abb. 9 Schematische Darstellung der Rückfaltung und Abflachung
Das Rückfalten und Flachdrücken erfolgt in der Regel in zwei Schritten: Zunächst wird das Material mit der Einlegematrize auf 30° gebogen und anschließend flachgedrückt.
Daher muss bei der Erstellung des Biegelinie Auf der erweiterten Zeichnung ist es wichtig, die Biegelinie auf der Grundlage der 150°-Biegung darzustellen, wie in Abbildung 9 gezeigt.
Tabelle 1: Biegekoeffizient von Blechen mit unterschiedlichen Dicken bei verschiedenen Biegewinkeln
| Winkel | Dicke/mm | ||||
|---|---|---|---|---|---|
| 1 | 1.2 | 1.5 | 1.8 | 2.5 | |
| 45° | 5.3 | 6.3 | 7.8 | 9.5 | 13 |
| 50° | 4.5 | 5.4 | 6.8 | 8.1 | 11.25 |
| 55° | 4 | 4.7 | 5.8 | 7.05 | 9.75 |
| 60° | 3.4 | 4.1 | 5.1 | 6.15 | 8.5 |
| 65° | 3 | 3.6 | 4.5 | 5.4 | 7.5 |
| 70° | 2.65 | 3.2 | 4 | 4.75 | 6.6 |
| 75° | 2.35 | 2.8 | 3.5 | 4.25 | 5.9 |
| 80° | 2.1 | 2.5 | 3.1 | 3.75 | 5.25 |
| 85° | 1.9 | 2.25 | 2.8 | 3.35 | 4.65 |
| 90° | 1.7 | 2 | 2.5 | 3 | 4.15 |
| 95° | 1.5 | 1.8 | 2.2 | 2.7 | 3.75 |
| 100° | 1.35 | 1.6 | 2 | 2.4 | 3.35 |
| 105° | 1.2 | 1.4 | 1.75 | 2.15 | 3 |
| 110° | 1.1 | 1.3 | 1.6 | 2 | 2.65 |
| 115° | 1 | 1.25 | 1.4 | 1.7 | 2.35 |
| 120° | 0.85 | 1 | 1.25 | 1.5 | 2.1 |
| 125° | 0.75 | 0.9 | 1.1 | 1.35 | 1.85 |
| 130° | 0.65 | 0.8 | 1 | 1.18 | 1.65 |
| 135° | 0.55 | 0.7 | 0.85 | 1.05 | 1.45 |
| 140° | 0.5 | 0.6 | 0.75 | 0.9 | 1.25 |
| 145° | 0.43 | 0.5 | 0.65 | 0.77 | 1.05 |
| 150° | 0.35 | 0.43 | 0.55 | 0.65 | 0.9 |
| 155° | 0.3 | 0.35 | 0.45 | 0.53 | 0.75 |
| 160° | 0.23 | 0.27 | 0.35 | 0.4 | 0.6 |
| 165° | 0.17 | 0.2 | 0.25 | 0.3 | 0.45 |
Die N-fache Verarbeitungsmethode umfasst sowohl die Umformung als auch die Abflachung, und der Algorithmus für die Entfaltung ist:
L = A + B + K
(K ist die Bogenlänge der neutralen Schicht).
λ = 0,5T
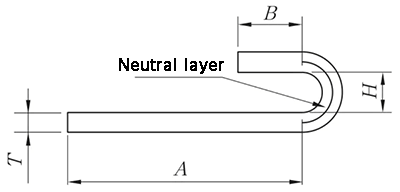
Abb.10 N-fach Diagramm
(1) Die Bogenausdehnung ist direkt K, und es wird die Bogenlänge der neutralen Schicht genommen. λ= 0,5T
(2) Erweiterung mit dem Lineal auf einer Seite.
L = A + K
(k ist die Bogenlänge der neutralen Schicht)
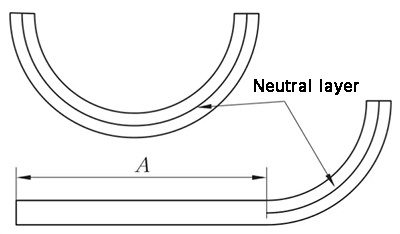
Abb. 11 Schematische Darstellung des Bogenbiegens
In der realen Produktion kann die präzise Kontrolle der abgewickelten Länge von Blechen durch 3D-Software hauptsächlich durch die folgenden Schritte und Methoden erreicht werden:
Wählen Sie die richtige 3D-Konstruktionssoftware: Zunächst müssen Sie eine 3D-CAD-Software auswählen, die für die Blechkonstruktion geeignet ist. SolidEdge, Creo, FreeCAD, UG usw. sind alles Software, die für die Blechkonstruktion verwendet werden kann. Diese Software bietet Blechmodule oder verwandte Funktionen, die den Konstrukteuren bei der Konstruktion und Abwicklungsberechnung von Blechteilen helfen können.
Verwenden Sie das Blechmodul oder die Werkzeuge in der Software: Die meisten 3D-CAD-Programme bieten entsprechende Werkzeuge und Funktionen für die Blechkonstruktion. Creo bietet beispielsweise eine Vielzahl von Methoden zur Steuerung der abgewickelten Abmessungen von Blechen, einschließlich der Modellierungs- und Abwicklungsmethoden für große Bogenblechteile, der Biegeabzugsmethode usw. FreeCAD, eine Open-Source-3D-Modellierungssoftware, bietet ebenfalls ein Blechmodul.
AppBerechnungsmethoden zur Entfaltung: Um die Genauigkeit der Länge nach dem Abwickeln des Blechs zu gewährleisten, können verschiedene Abwicklungsberechnungsmethoden verwendet werden. Zu den gängigen Methoden gehören die Biegekompensationsmethode, die Biegeabzugsmethode und die K-Faktor-Berechnungsmethode. Diese Methoden können den Konstrukteuren helfen, die tatsächliche Länge des Materials im abgewickelten Zustand zu berechnen und damit die erwartete Größe der Teile nach dem endgültigen Biegen und Formen zu gewährleisten.
Achten Sie auf die Handhabung von Kanten und Ecken und die Anpassung von Details: Bei der Konstruktion von Blechen sind die Details der Kanten- und Eckenbearbeitung sehr wichtig. Einige Software, wie z. B. SW, bietet eine Vielzahl von Lösungen für die Kanten- und Eckenbearbeitung und Biegemethoden, die zur Verbesserung der Abwicklungsgenauigkeit beitragen.
Zu den üblichen Biegewinkeln für Biegungen, die nicht 90 Grad betragen, gehören 45 Grad und 135 Grad, sind aber nicht darauf beschränkt. Die Berechnungsmethode für den K-Faktor basiert auf dem Verhältnis zwischen Materialdicke und Biegeradius.
Genauer gesagt ist der K-Faktor = δ / T, wobei δ für die Materialdicke und T für den Biegeradius steht. Diese Methode ist für die Berechnung des Biegekoeffizienten eines beliebigen Winkels, der nicht 90 Grad beträgt, anwendbar.
In der Praxis wird aufgrund der möglichen Unterschiede und großen Fehler bei den Abzugswerten von Biegungen unter verschiedenen Winkeln im Allgemeinen der K-Faktor als Biegekoeffizient verwendet.
Außerdem sind Anpassungen erforderlich, um den K-Faktor-Wert für unterschiedliche Blechdicken genau zu bestimmen. In einigen Referenzen wird darauf hingewiesen, dass der K-Faktor-Wert für einen beliebigen Biegeradius durch spezielle Interpolationstechniken berechnet werden kann, die sich bei industriellen Blechanwendungen bewährt haben.
Die Berechnungsformel für die aufgeweitete Länge von abgeschrägten Abkantblechen lautet: [L = A + B + C + 0,2], wobei (A), (B) und (C) die Innenmaße darstellen und 0,2 als Ausgleichswert dient.
Basierend auf den allgemeinen Grundsätzen und Praktiken der Blechausdehnungsberechnung berücksichtigt dieser Ausgleichswert Abweichungen zwischen der tatsächlichen und der theoretisch berechneten Länge, die auf Faktoren wie Materialbiegung und Fehler in der Formgenauigkeit während des realen Betriebs zurückzuführen sind.
Bei der Blechbearbeitung trägt dieser Ausgleichswert dazu bei, die Maßhaltigkeit und Qualität des Endprodukts zu gewährleisten.
Blechteile werden in großem Umfang in der elektromechanischen Industrie, der Leichtindustrie und der Automobilindustrie verwendet.
Die ungefaltete Form der Blechteile ist der wichtigste Faktor für die Größe des Rohlings, die wiederum die Größe und Form des Rohlings beeinflusst.
Herkömmliche Verfahren zum Abwickeln von Blechteilen sind jedoch aufgrund ihrer langen Zyklen, geringen Effizienz und schlechten Qualität zunehmend ungeeignet, um die Anforderungen moderner Konstruktionen zu erfüllen.
Um diese Unzulänglichkeiten zu beheben, hat sich in den letzten Jahren der Einsatz moderner CAD-Systeme durchgesetzt.
Diese spezialisierten Systeme für die Konstruktion von Blechteilen zeichnen sich durch eine robuste Funktionalität aus und können den Zeit- und Arbeitsaufwand für die vorläufige Konstruktion und den Einsatz von Blechteilen erheblich reduzieren.