Wie misst man die Geradheit einer Führungsschiene, um einen präzisen Maschinenbetrieb zu gewährleisten? In diesem Artikel werden zwei gängige Methoden untersucht: die Methode der Verbindung von zwei Endpunkten und die Methode der Mindestbedingungen. Durch den Vergleich dieser Verfahren erfahren Sie, wie die einzelnen Verfahren Geradheitsfehler bewerten und warum die Wahl des richtigen Verfahrens für genaue Messungen entscheidend ist. Informieren Sie sich über die Vor- und Nachteile der beiden Methoden und finden Sie heraus, welche Methode am besten geeignet ist, um eine optimale Geradheit bei Ihren technischen Projekten zu erzielen.
In der technischen Praxis gibt es zwei gängige Methoden zur Bewertung des Geradheitsfehlers von Führungsschienen: die Zwei-Endpunkt-Verbindungsmethode und die Methode der Mindestbedingungen.
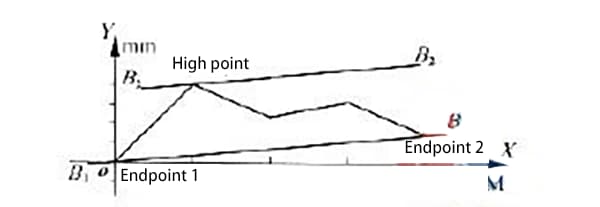
Bei der Methode der Zwei-Endpunkte-Verbindung wird die Fehlerkurve Ende-zu-Ende verbunden, dann werden zwei Linien parallel zur Ende-zu-Ende-Linie am höchsten und niedrigsten Punkt der Kurve gezogen und die Werte entlang der vertikalen Achse zwischen den beiden parallelen Linien gemessen.
Nach der Datenverarbeitung ist der Wert der Geradheitsfehler der Führungsschiene.
Die Methode der minimalen Bedingung verbindet die Punkte "hoch, hoch" (oder "niedrig, niedrig") der Fehlerkurve und zieht eine Linie parallel dazu durch den niedrigen (hohen) Punkt.
Der Wert, der zwischen den beiden parallelen Linien entlang der vertikalen Achse gemessen wird, ist der Geradheitsfehler der Führungsschiene nach der Datenverarbeitung.
Bei der Methode der Mindestbedingungen handelt es sich um eine schiedsrichterliche Bewertung.
Die Methode der Zwei-Endpunkte-Verbindung ist keine Arbitrage-Bewertung, wird aber wegen ihrer Einfachheit und Bequemlichkeit bei der Bewertung häufig in der Produktion verwendet, obwohl sie manchmal große Fehler produzieren kann.
In diesem Artikel wird der Grenzwert des Fehlers erörtert, der zwischen diesen beiden Bewertungsmethoden entsteht.
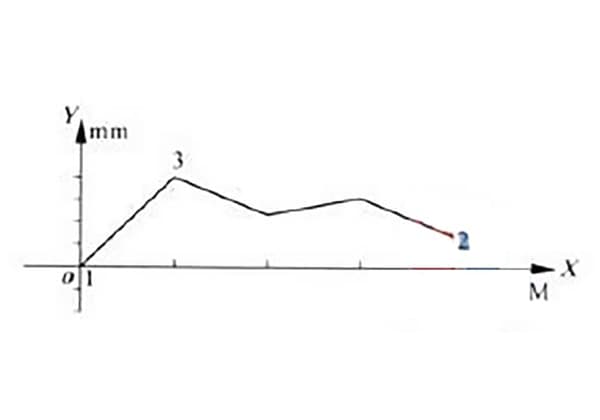
Bei der Messung des Geradheitsfehlers eines bestimmten Modells einer hydraulischen Gleitschienenführung wurde die Geradheitsfehlerkurve wie in Abbildung 1 dargestellt ermittelt.
Wie aus der Abbildung ersichtlich ist, liegt die Fehlerkurve auf der gleichen Seite wie die beiden Enden der Linie.
Nachfolgend wird der Geradheitsfehlerwert der Führungsschiene mit Hilfe der Methode der Mindestbedingungen und der Methode der Zwei-End-Verbindung bewertet.
(1) Bewertung des Geradheitsfehlers nach der Methode der Mindestbedingungen
Nach der Methode der Mindestbedingungen werden die tiefsten Punkte 1 und 2 der Kurve in Abbildung 1 (wobei der tiefste Punkt 1 mit dem Ursprung zusammenfällt) durch die Linie a1a1 verbunden, wie in Abbildung 2 dargestellt.
Die Parallele a2a2 wird durch den höchsten Punkt 3 in Bezug auf die Linie a1a1 gezogen.
Der entlang der y-Achse gemessene Wert in dem Bereich, der von den beiden parallelen Linien a1a1 und a2a2 eingeschlossen wird, stellt nach der Verarbeitung der Daten den Geradheitsfehler der Führungsschiene δ dar, der sich aus der Methode der Mindestbedingungen ergibt.
(2) Bewertung des Geradheitsfehlers mit der Methode der Zwei-End-Verbindung
Nach der Methode der Zwei-Enden-Verbindung sind die Enden der Kurve in Abbildung 1 auch die Endpunkte 1 und 2 der Kurve, wie in Abbildung 3 dargestellt.
Die Endpunkte 1 und 2 werden durch die Linie b1b1 verbunden, und dann wird eine parallele Linie b2b2 durch den höchsten Punkt gezogen.
Der entlang der y-Achse gemessene Wert in dem Bereich, der von den beiden parallelen Linien b1b1 und b2b2 eingeschlossen wird, stellt nach der Verarbeitung der Daten den Geradheitsfehler der Führungsschiene δ dar, der sich aus der Methode der Verbindung zweier Enden ergibt.
(3) Bestimmung der Fehlergrenze, die sich aus den beiden Bewertungsmethoden ergibt
Da beide Bewertungsmethoden zur Bestimmung des Geradheitsfehlers derselben Führungsschiene verwendet werden, entsprechen der "untere Punkt 1", der "untere Punkt 2" und der "obere Punkt 3" in Abbildung 2 jeweils dem "Endpunkt 1", dem "Endpunkt 2" und dem "oberen Punkt 3" in Abbildung 3. Dadurch fällt die Linie a1a1 mit der Linie b1b1 und die Linie a2a2 mit der Linie b2b2 zusammen.
Daher ist der von den beiden Bewertungsmethoden erzeugte Fehlerwert gleich Null.
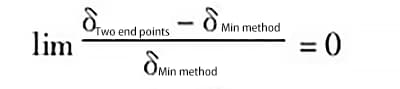
Wenn die Fehlerkurve auf der gleichen Seite wie die beiden Enden der Linie liegt, ist die von den beiden Bewertungsmethoden erzeugte Fehlergrenze gleich Null, was bedeutet, dass die von den beiden Methoden erzielten Bewertungsergebnisse gleich sind.
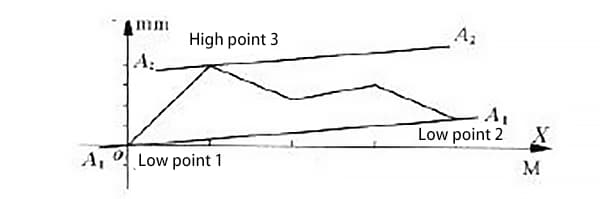
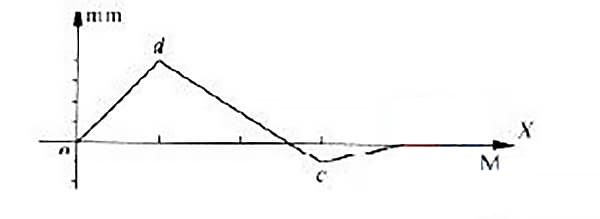
In der gemessenen Geradheitsfehlerkurve einer Führungsschiene liegen einige Fehlerkurven auf beiden Seiten der Verbindungslinie zwischen den Enden, wie in Abbildung 4 dargestellt.
Die Fehlerkurve dieser Führungsschiene hat eine Verbindungslinie zwischen ihren Enden, die mit der x-Achse zusammenfällt. Der Geradheitsfehler der Führungsschiene wird mit der Methode der minimalen Bedingung und der Methode der Zwei-End-Verbindung bewertet.
Wie aus Abbildung 4 ersichtlich ist, sind die Punkte o und c die beiden Tiefpunkte und die beiden Endpunkte der Kurve, während Punkt d der höchste Punkt ist.
Nach der Methode der Mindestbedingungen werden die Punkte o und c durch die Linie a1a1 verbunden, wie in Abbildung 5 dargestellt. Die Linie a2a2 wird parallel zur Linie a1a1 durch den höchsten Punkt d gezogen.
Der entlang der y-Achse gemessene Wert in dem Bereich, der von den beiden parallelen Linien a1a1 und a2a2 eingeschlossen wird, stellt nach der Verarbeitung der Daten den Geradheitsfehler der Führungsschiene δ dar, der sich aus der Methode der Mindestbedingungen ergibt.
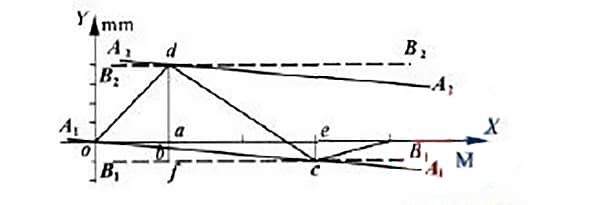
Zeichnen Sie nach der Methode der Zweipunktverbindung zwei zur x-Achse parallele Linien, die jeweils durch die Punkte C und D verlaufen.
Diese Linien werden durch die gestrichelten Linien b1b1 und b2b2 in Abbildung 5 dargestellt. In dem von diesen beiden parallelen Linien eingeschlossenen Bereich stellt der nach der Datenverarbeitung entlang der y-Achse gemessene Wert den Geradheitsfehlerwert der Führungsschiene zwischen den beiden Endpunkten dar.
Um die Methode der Mindestabweichung und den Wert der Abweichung an den beiden Endpunkten zu bestimmen, zeichnen Sie eine Linie parallel zur y-Achse, die durch den Punkt D verläuft, die Achse im Punkt A schneidet, die Linie a1a1 im Punkt H schneidet und die Linie b1b1 im Punkt F schneidet.
Zeichnen Sie ebenfalls eine zur y-Achse parallele Linie, die durch den Punkt C verläuft und die Achse im Punkt E kreuzt.
(1) Bestimmung des Geradheitsfehlers mit der Methode der Mindestbedingungen
Nach der Methode der minimalen Bedingung wird der Geradheitsfehlerwert δ der Führungsschiene aus dem nach der Datenverarbeitung entlang der y-Achse gemessenen Wert abgeleitet, was die Methode der minimalen Abweichung darstellt.
Wie in Abbildung 5 dargestellt:
Und da BD = BA + AD,
∆OAB und ∆OEC sind also zwei ähnliche Dreiecke,
Durch Umstellen von Gleichung (3) erhalten wir:
Wenn man Gleichung (4) in Gleichung (2) einsetzt und umrechnet, erhält man:
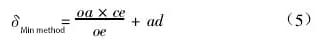
(2) Bestimmung des Geradheitsfehlers mit der Zwei-Punkt-Verbindungsmethode
Nach der Methode der Zweipunktverbindung stellt der nach der Datenverarbeitung entlang der y-Achse gemessene Wert den Geradheitsfehlerwert δ der Führungsschiene zwischen den beiden Endpunkten dar.
Wie in Abbildung 5 dargestellt:
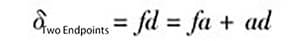
Und da fa = ce,
(3) Berechnung der Fehlerwerte, die durch zwei Bewertungsmethoden erzeugt werden
Gleichung (6) minus Gleichung (5), d.h.,
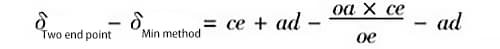
Wenn wir umrechnen, erhalten wir:
(4) Berechnung des maximalen Fehlers, der durch zwei Bewertungsmethoden erzeugt wird
In Abbildung 5 sei ad = δ1, ce = δ2, oa = p; die Länge der zu messenden Führungsschiene sei l, dann sei oe = l - p, und:
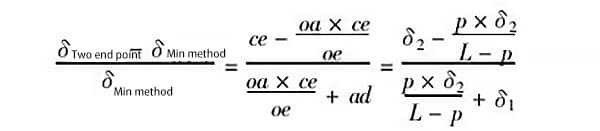
Wenn z.B. p = 0,5 m (d.h. der Abstand beträgt 0,5 m), δ1 = 1,0δ, δ2 = 0,25δ und die Länge der gemessenen Führungsschiene l - 2 m beträgt, dann ist das Verhältnis der durch die beiden Bewertungsmethoden erzeugten Fehler gleich:
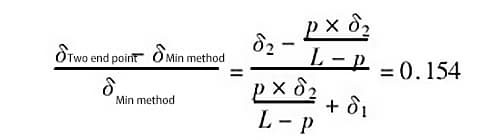
Das Verhältnis der durch die beiden Bewertungsmethoden erzeugten Fehler beträgt 0,154, was bedeutet, dass der durch die Zwei-Punkt-Verbindungsmethode erzeugte Fehler um 15,4% größer ist als der durch die Mindestbedingungsmethode erzeugte.
In der obigen Gleichung, wenn 
, d. h. der höchste und der niedrigste Punkt der Fehlerkurve liegen unendlich weit auseinander, dann
so erhalten wir:
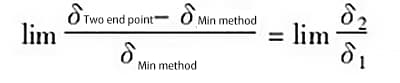
Wenn zum Beispiel δ1 = 1,0δ und δ2 = 0,25δ und der Abstand zwischen dem höchsten und dem niedrigsten Punkt der Fehlerkurve unendlich groß ist (d.h. L=0,25), dann ist das Verhältnis der Fehler, die durch die beiden Bewertungsmethoden erzeugt werden 
Das bedeutet, dass der Fehler, der durch die Zweipunktverbindungsmethode entsteht, 25% größer ist als der Fehler, der durch die Methode der Mindestbedingungen entsteht.
Wenn δ1 = δ2, d.h. der Abstand zwischen dem höchsten und dem niedrigsten Punkt der Fehlerkurve gleich ist, wie in Abbildung 6 dargestellt, dann sind die maximalen Fehlerwerte, die von den beiden Bewertungsmethoden erzeugt werden:
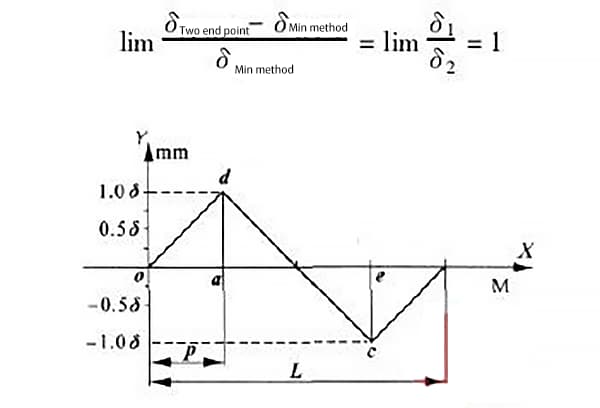
Daraus ist ersichtlich, dass der maximale Fehler, der durch die beiden Bewertungsmethoden erzeugt wird, am größten ist und 100% erreichen kann, wenn der höchste und der niedrigste Punkt der Führungsschiene gleich und unendlich weit voneinander entfernt sind.
In Tabelle 1 ist das Verhältnis der von den beiden Auswerteverfahren erzeugten Fehler für verschiedene Längen der gemessenen Führungsschiene aufgeführt, wenn die Punkte der Fehlerkurve auf beiden Seiten der Zweipunktverbindungslinie verteilt sind.
Der Abstand zwischen dem höchsten und dem niedrigsten Punkt der Fehlerkurve ist gleich, wenn der Messabstand p = 0,5 ist.
Tabelle 1 Fehlerquote der beiden Bewertungsmethoden
| Fehlerquote | Abstand L (M) zwischen dem höchsten und dem niedrigsten Punkt der Führungsschiene | ||||||
| 1 | 10 | 15 | 20 | 25 | 30 | 40 | ∞ |
 | 33.30% | 90% | 93.30% | 95% | 96% | 96.70% | 97.50% |
Wenn die Punkte auf der Geradheitsfehlerkurve auf derselben Seite der Zweipunkt-Verbindungslinie liegen, dann sind die von den beiden Bewertungsmethoden erzeugten Fehler gleich Null, d. h. die Ergebnisse der beiden Bewertungsmethoden sind gleich.
Wenn die Punkte auf der Geradheitsfehlerkurve auf beiden Seiten der Zweipunkt-Verbindungslinie liegen und der höchste und der niedrigste Punkt der Fehlerkurve gleich groß und unendlich weit voneinander entfernt sind, dann ist der von den beiden Bewertungsmethoden erzeugte maximale Fehler am größten, und der von der Zweipunkt-Verbindungsmethode erzeugte Fehler kann 100% höher sein als der von der Methode der Mindestbedingungen erzeugte.
Daher ist es bei der Bewertung des Geradheitsfehlers großer Werkzeugmaschinen-Führungsschienen in der praktischen Produktion sehr wichtig, die geeignete Bewertungsmethode zu wählen. Wenn die Punkte auf der Fehlerkurve auf beiden Seiten der Zweipunktverbindungslinie liegen, sollte die Methode der minimalen Bedingung als erste Wahl für die Bewertung verwendet werden.
Als Gründer von MachineMFG habe ich mehr als ein Jahrzehnt meiner Karriere der metallverarbeitenden Industrie gewidmet. Meine umfangreiche Erfahrung hat es mir ermöglicht, ein Experte auf den Gebieten der Blechverarbeitung, der maschinellen Bearbeitung, des Maschinenbaus und der Werkzeugmaschinen für Metalle zu werden. Ich denke, lese und schreibe ständig über diese Themen und bin stets bestrebt, in meinem Bereich an vorderster Front zu bleiben. Lassen Sie mein Wissen und meine Erfahrung zu einem Gewinn für Ihr Unternehmen werden.
DE 
EN 
AR 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO