Festigkeit und Steifigkeit in der Werkstoffmechanik verstehen

Vorwort

Um die optimale Leistung und Zuverlässigkeit eines mechanischen Systems oder einer Struktur zu gewährleisten, muss jede Komponente die ihr zugedachte Funktion effektiv und effizient erfüllen. Das Hauptziel der Sicherheitskonstruktion von Bauteilen besteht darin, zu gewährleisten, dass alle Elemente über eine angemessene Festigkeit, Steifigkeit und Stabilität verfügen, um so die Gesamtintegrität und Langlebigkeit des Systems sicherzustellen.

Stabilität ist ein grundlegendes Konzept in der Technik und bezieht sich auf die Fähigkeit eines Bauteils, seinen ursprünglichen Gleichgewichtszustand beizubehalten oder wiederherzustellen, wenn es äußeren Kräften ausgesetzt ist. Dieses Prinzip ist in verschiedenen Szenarien von entscheidender Bedeutung, z. B.:

1. Die plötzliche seitliche Verformung einer schlanken Säule unter axialem Druck (Euler-Knickung)
2. Der Einsturz einer Gebäudesäule aufgrund von Tragwerksversagen (strukturelle Instabilität)
3. Das Beulen von dünnwandigen Bauteilen unter Druck- oder Scherbeanspruchung (lokales oder globales Beulen)

Diese Beispiele verdeutlichen, wie wichtig die Stabilität ist, um katastrophale Ausfälle zu verhindern und den sicheren Betrieb von mechanischen Systemen und Strukturen zu gewährleisten.

In dieser Diskussion werde ich mich darauf konzentrieren, mein umfassendes Verständnis von zwei ebenso wichtigen technischen Prinzipien zu erläutern: Steifigkeit und Festigkeit. Diese Konzepte bilden zusammen mit der Stabilität den Dreiklang grundlegender Überlegungen bei der Sicherheitskonstruktion von Bauteilen, wobei jedes von ihnen eine entscheidende Rolle bei der Bestimmung der Gesamtleistung, Haltbarkeit und Sicherheit von technischen Systemen spielt.

Stärke

Was ist Stärke?

Definition: Festigkeit ist die Fähigkeit von Materialien, Bauteilen oder Strukturen, einwirkenden Lasten oder Kräften ohne Versagen, übermäßige Verformung oder Beschädigung standzuhalten. Sie ist eine grundlegende Eigenschaft in der Materialwissenschaft und -technik, die die Fähigkeit eines Materials bestimmt, mechanischen Belastungen standzuhalten.

Stärke umfasst verschiedene Aspekte, darunter:

1. Zugfestigkeit: Die maximale Spannung, die ein Material bei Dehnungskräften aushalten kann, bevor es versagt.
2. Druckfestigkeit: Die maximale Spannung, die ein Material bei Druckbeanspruchung aushalten kann, bevor es versagt.
3. Streckgrenze: Die Spannung, bei der ein Material beginnt, sich plastisch zu verformen.
4. Scherfestigkeit: Die Fähigkeit, Kräften zu widerstehen, die ein inneres Gleiten eines Materials entlang einer Ebene parallel zur Kraftrichtung verursachen.

In der Metallverarbeitung zum Beispiel ist die Kenntnis der Festigkeit von Werkstoffen entscheidend für die Konstruktion von Bauteilen, die betrieblichen Belastungen standhalten können. Ein Stahlträger in einem Gebäude muss eine ausreichende Festigkeit aufweisen, um das Gewicht der Struktur und zusätzliche Lasten zu tragen, ohne sich zu verbiegen oder zu brechen.

Die Stärke wird von verschiedenen Faktoren beeinflusst, darunter:

• Materialzusammensetzung und Mikrogefüge
• Wärmebehandlung und Verarbeitungsmethoden
• Umweltbedingungen (Temperatur, Korrosion)
• Ladegeschwindigkeit und -dauer

Die Maßeinheit für die Festigkeit wird in der Regel in Megapascal (MPa) oder in Pfund pro Quadratzoll (psi) in Zoll ausgedrückt. Baustahl beispielsweise hat eine Zugfestigkeit von etwa 400-550 MPa, während hochfeste legierte Stähle 1000 MPa überschreiten können.

In der Fertigung und im Maschinenbau sind Festigkeitsberechnungen und -prüfungen unerlässlich:

• Auswahl geeigneter Materialien für bestimmte Anwendungen
• Entwurf von Komponenten mit optimalen Leistungs- und Sicherheitsfaktoren
• Vorhersage von Produktlebensdauer und Ausfallmodi
• Gewährleistung der Einhaltung von Industrienormen und -vorschriften

Fortgeschrittene Techniken wie die Finite-Elemente-Analyse (FEA) und zerstörende Prüfungen werden häufig eingesetzt, um die Festigkeit von Materialien und Komponenten in komplexen technischen Anwendungen zu bewerten und zu validieren.

Versagensarten auf Basis der Festigkeit

Sprödbruch: Eine plötzliche und katastrophale Versagensart, die durch eine schnelle Rissausbreitung mit minimaler plastischer Verformung gekennzeichnet ist. Diese Art von Versagen tritt ohne Vorwarnung auf und führt normalerweise zu einer sauberen, flachen Bruchfläche.

Zum Beispiel:

1. Der abrupte Bruch einer Gusseisenprobe entlang ihres Querschnitts während eines einachsigen Zugversuchs, der an der Bruchfläche ein kristallines Aussehen aufweist.
2. Das plötzliche Versagen einer Gusseisenprobe mit kreisförmigem Querschnitt entlang einer schrägen Ebene während eines Torsionsversuchs, das ein schraubenförmiges Bruchbild zeigt.

Plastische Ausbeute: Ein Versagensmodus, bei dem das Material eine erhebliche plastische Verformung erfährt, was zu einer dauerhaften Formveränderung und einem Verlust der strukturellen Integrität führt. Diese Art des Versagens ist im Vergleich zum Sprödbruch in der Regel allmählicher und besser zu beobachten.

Zum Beispiel:

1. Bei der Zugprüfung zeigt eine Probe aus kohlenstoffarmem Stahl vor dem endgültigen Versagen eine beträchtliche Einschnürung und Dehnung mit einer charakteristischen Becher-Kegel-Bruchfläche.
2. Bei Torsion erfährt eine Probe aus kohlenstoffarmem Stahl vor dem Versagen eine erhebliche Winkelverformung und Verformung, die oft mit sichtbaren Oberflächenverformungen einhergeht.

Es ist wichtig zu wissen, dass der Versagensmodus eines Materials von verschiedenen Faktoren abhängt, darunter Materialeigenschaften, Belastungsbedingungen, Temperatur und Umweltfaktoren. Einige Werkstoffe können unter bestimmten Bedingungen, z. B. bei niedrigen Temperaturen oder hohen Dehnungsgeschwindigkeiten, einen Übergang von duktilem zu sprödem Verhalten zeigen.

Theorie der Stärke

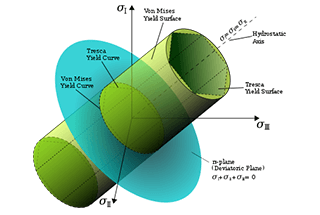
1. Theorie der maximalen Zugspannung:

Wenn die maximale Zugspannung σ1 an einem Punkt des Bauteils die Bruchspannung σb unter unidirektionalen Spannungsbedingungen erreicht, bricht das Material spröde. Die Kriterien für das Sprödbruchversagen von Bauteilen mit kritischen Punkten unter komplexen Spannungsbedingungen sind also: σ1 = σb.

Folglich sind die in der ersten Richtlinie festgelegten Festigkeitsbedingungen Festigkeitstheorie sind: σ1 ≤ σb.

2. Theorie der maximalen Zugbeanspruchung:

Wenn die maximale Zugdehnung ε1 unter einseitig gerichteten Spannungsbedingungen den Grenzwert εu erreicht, versagt das Material aufgrund von Sprödbruch. Dies kann als ε1 = εu ausgedrückt werden.

Aus dem verallgemeinerten Hooke'schen Gesetz können wir ε1 berechnen als: ε1 = [σ1 - u(σ2 + σ3)] / E, also σ1 - u(σ2 + σ3) = σb.

Die durch die zweite Festigkeitstheorie festgelegten Festigkeitsbedingungen sind: σ1 - u(σ2 + σ3) ≤ σb.

3. Theorie der maximalen Scherspannung:

Wenn die maximale Schubspannung τMax unter einseitig gerichteten Spannungsbedingungen die Bruchschubspannung τ0 erreicht, versagt das Material aufgrund von Fließen. Dies kann als τMax = τ0 ausgedrückt werden.

Die Formel für die Schubspannung auf einem geneigten Querschnitt bei axialem Zug lautet τ0 = σs/2 (σs ist die Normalspannung auf dem Querschnitt). Die Formel für τMax ist (σ1 - σ3)/2. Die Schädigungsbedingung kann also als σ1 - σ3 = σs umgeschrieben werden.

Die durch die dritte Festigkeitstheorie festgelegte Festigkeitsbedingung lautet: σ1 - σ3 ≤ σs.

4. Theorie der spezifischen Energie der Formveränderung:

Erreicht das Formänderungsverhältnis an einer Stelle des Bauteils unter einseitig gerichteten Spannungsbedingungen den Grenzwert, versagt das Material aufgrund von Fließverhalten.

Die nach der vierten Festigkeitstheorie ermittelte Festigkeitsbedingung lautet:

√(σ1^2 + σ2^2 + σ3^2 - σ1σ2 - σ2σ3 - σ3σ1) < σs.

2. Steifigkeit

Was ist Steifigkeit?

Definition: Die Steifigkeit bezeichnet die Fähigkeit eines Materials, Bauteils oder einer Struktur, einer elastischen Verformung oder Verschiebung zu widerstehen, wenn sie einer äußeren Kraft ausgesetzt sind. Sie quantifiziert das Ausmaß, in dem ein System seine Form und seine Abmessungen innerhalb zulässiger Grenzen unter einwirkenden Belastungen beibehalten kann.

Die Steifigkeit ist ein grundlegender Parameter in der Technik, der das Verhältnis zwischen Kraft und Verformung in einem Material oder einer Struktur charakterisiert. Sie ist definiert als das Verhältnis zwischen der aufgebrachten Kraft und der daraus resultierenden Verschiebung und gibt an, wie viel Kraft erforderlich ist, um eine Verformungseinheit zu erzeugen. Mathematisch gesehen wird die Steifigkeit (k) wie folgt ausgedrückt:

k = F / δ

Wo:

• F = angewandte Kraft
• δ = resultierende Verschiebung

Die Einheit der Steifigkeit ist in der Regel die Kraft pro Längeneinheit, z. B. N/m (Newton pro Meter) im SI-System oder lbf/in (pounds-force per inch) im imperialen System.

In der Praxis kann die Steifigkeit mit Hilfe der Analogie zu einer Feder konzeptualisiert werden. Die Federkonstante, die die Steifigkeit einer Feder darstellt, ist definiert als das Verhältnis zwischen der aufgebrachten Zug- oder Druckkraft und der daraus resultierenden Dehnung oder Stauchung. Dieses Verhältnis wird durch das Hooke'sche Gesetz für linear elastische Systeme beschrieben.

Das Verständnis und die Kontrolle der Steifigkeit sind bei verschiedenen technischen Anwendungen von entscheidender Bedeutung, z. B:

1. Tragwerksplanung: Sicherstellen, dass Gebäude und Brücken den Belastungen ohne übermäßige Verformung standhalten können
2. Mechanische Komponenten: Konstruktion von Teilen, die auch unter Betriebsbelastung präzise bleiben
3. Schwingungsüberwachung: Steuerung der dynamischen Reaktion von Systemen auf zyklische Belastungen
4. Materialauswahl: Auswahl geeigneter Materialien für bestimmte Anwendungen auf der Grundlage ihrer Steifigkeitseigenschaften

Ingenieure müssen die Anforderungen an die Steifigkeit mit anderen konstruktiven Überlegungen wie Festigkeit, Gewicht, Kosten und Herstellbarkeit in Einklang bringen, um optimale Lösungen für bestimmte Anwendungen zu finden.

Art der Steifigkeit:

Wenn die aufgebrachte Last konstant ist, wird sie als statische Steifigkeit bezeichnet.

Wenn die Last wechselt, spricht man von dynamischer Steifigkeit.

Die statische Steifigkeit umfasst die strukturelle Steifigkeit und die Kontaktsteifigkeit.

Die strukturelle Steifigkeit bezieht sich auf die Steifigkeit des Bauteils selbst und umfasst die Biegesteifigkeit und die Torsionssteifigkeit.

1. Biegesteifigkeit: berechnet nach der folgenden Formel:

K=P/δ

Wo

• P - statische Belastung (n);
• δ-- Elastische Verformung in Lastrichtung（ μm)。

2. Die Torsionssteifigkeit wird nach der folgenden Formel berechnet:

K_m=ML/θ

Wobei M - angewandtes Drehmoment (n - m);

L - Abstand zwischen der Position der Drehmomenteinwirkung und dem festen Ende (m);

θ-- Verdrehungswinkel (°)

3. Verhältnis zwischen Festigkeit und Steifigkeit

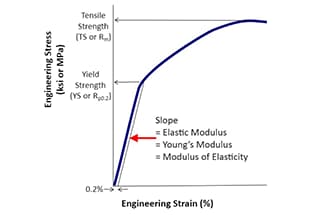
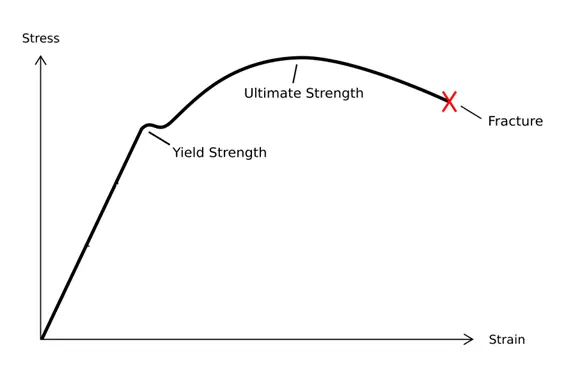
Aus der obigen Erläuterung von Festigkeit und Steifigkeit geht hervor, dass sich die Festigkeit auf das Versagen unter äußerer Krafteinwirkung konzentriert und in plastisches Fließ- und Sprödbruchversagen unterteilt wird, was mit der Spannungs-Dehnungs-Kurve bei Zugversuchen zusammenhängt. Im Vergleich dazu bezieht sich die Steifigkeit auf das Verhältnis zwischen Verformung und Kraft.

Wie in der Abbildung dargestellt.

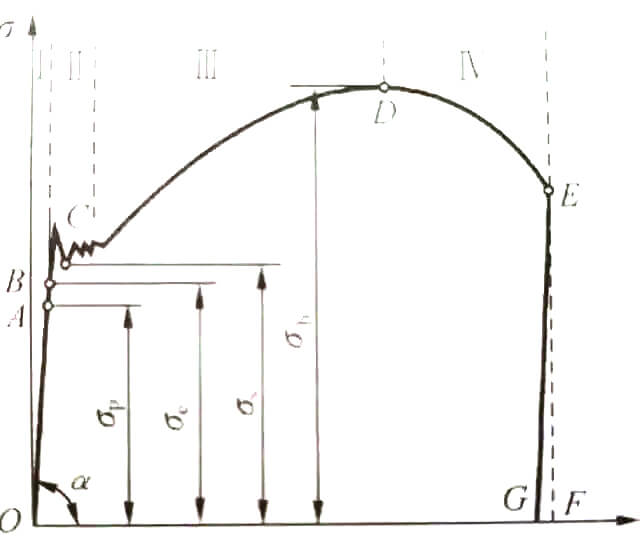
Die Kurve in der Abbildung lässt sich in vier Stufen unterteilen:

1. Stadium der elastischen Verformung;

2. Ertragsstufe;

3. Verstärkungsphase;

4. Lokales Einschnürungsstadium.

Die Steifigkeit ist definiert als Widerstand gegen elastische Verformung, die in der Anfangsphase auftritt und unter elastischen Bedingungen durch das Hooke'sche Gesetz bestimmt wird.

Berechnung der Biegesteifigkeit und Torsionssteifigkeit unter statische Lasten ähnelt dem Hooke'schen Gesetz, was darauf hindeutet, dass die Steifigkeit nur in der Phase der elastischen Verformung gemessen wird.

In der nächsten Phase, wenn die plastische Verformung während des Zugversuchs auftritt, verschwindet die Restdehnung nicht. Auf der Spannungs-Dehnungs-Kurve bleibt die Spannung zwar fast unverändert, aber die Dehnung nimmt deutlich zu. An diesem Punkt erreicht die Spannung die Fließgrenze und das Material tritt in das Stadium des plastischen Fließversagens ein. Wenn die Spannung weiter ansteigt, nimmt auch die Dehnung zu, bis sie die Festigkeitsgrenze erreicht.

Daher erfolgt die Messung der Festigkeit, nachdem das Material elastisch verformt wurde und bevor es die Festigkeitsgrenze erreicht.

Einpacken

Zusammenfassend lässt sich sagen, dass sowohl die Steifigkeit als auch die Festigkeit während der Versagensphase von Bauteilen bewertet werden, wobei die Steifigkeit anhand der Spannung und die Festigkeit anhand der Verformung gemessen wird.

Was die Reihenfolge im Verformungsprozess angeht, so tritt die Steifigkeit in der früheren Phase auf, während die Festigkeit in der späteren Phase auftritt.

Bei der Bewertung der Versagensbedingungen von Bauteilen sollte das Bauteil, solange die Steifigkeitsanforderungen erfüllt sind, in der Lage sein, während der elastischen Verformungsphase ausreichenden Spannungen standzuhalten, was wiederum die Festigkeitsanforderungen erfüllen sollte.

Diese Beziehung spiegelt sich in verschiedenen Konstruktionen wider, z. B. in der Welle von mechanischen Geräten. Normalerweise wird die Größe der Welle auf der Grundlage der Festigkeitsbedingungen bestimmt und ihre Steifigkeit auf der Grundlage der Steifigkeitsbedingungen überprüft.

Daher sind die Anforderungen an die Steifigkeit von Präzisionsmaschinenwellen sehr hoch, und die Auslegung der Querschnittsgröße wird häufig durch die Steifigkeitsbedingungen bestimmt.