Stellen Sie sich vor, Sie wüssten genau, wie viel Spannung Ihre Metallteile aushalten, ohne sie aufzuschneiden. Die Röntgeneigenspannungsmessung bietet diesen Einblick durch den Einsatz zerstörungsfreier Prüfverfahren. In diesem Artikel wird untersucht, wie Röntgenbeugungstechniken Eigenspannungen genau messen und so die Zuverlässigkeit und Langlebigkeit von Produkten verbessern. Erfahren Sie, wie verschiedene Methoden wie die sin²ψ- und cosα-Methode präzise Spannungsdaten liefern und so sicherstellen, dass Ihre Metallteile den höchsten Standards entsprechen. Tauchen Sie ein in diese fortschrittlichen Messverfahren, um ihre Prinzipien, Anwendungen und Vorteile für die Industrietechnik zu verstehen.
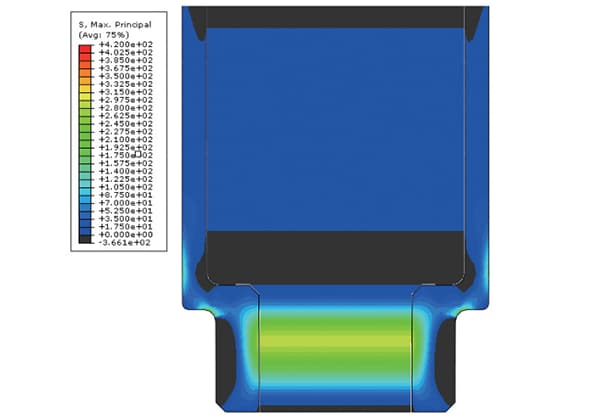
Eigenspannungen sind eine Art von inneren Spannungen, die in der Technik als solche bezeichnet werden. Die Verteilung von Eigenspannungen in einem Werkstück ist oft ungleichmäßig, was sich erheblich auf die statische Festigkeit, die Ermüdungsfestigkeit, die Formstabilität und die Korrosionsbeständigkeit auswirken kann. Daher ist die Messung der Eigenspannung von entscheidender Bedeutung.
Es gibt zwei Hauptmethoden zur Messung EigenspannungZerstörende Prüfung und zerstörungsfreie Prüfung. Bei der zerstörenden Prüfung wird ein Teil des Werkstücks entfernt und die Eigenspannung auf der Grundlage der entsprechenden Dehnung und Verschiebung. Zu den üblichen zerstörenden Prüfverfahren gehören die Bohren Methode und Ringkernmethode.
Bei der zerstörungsfreien Prüfung wird eine Beziehung zwischen der Eigenspannung und einer physikalischen Größe hergestellt, die eine Veränderung des Materials bewirken kann (z. B. Abstand der Kristallebenen, Ausbreitungsgeschwindigkeit der Ultraschallwellen oder magnetische Permeabilität), um die Eigenspannung zu berechnen. Zu den zerstörungsfreien Prüfverfahren gehören Röntgenbeugung, Neutronenbeugung, magnetische und Ultraschallverfahren.
Die Röntgenbeugung ist die am weitesten verbreitete Methode zur Messung von Eigenspannungen, da sie auf ausgereiften Prinzipien und bewährten Methoden beruht und immer ausgefeiltere Prüfgeräte zur Verfügung stehen, darunter Laborgeräte, tragbare Geräte für Messungen vor Ort und Spezialgeräte für besondere Umstände.
Die Röntgenbeugungsmethode zur Messung von Eigenspannungen wurde erstmals 1929 von dem russischen Wissenschaftler Akchenov vorgeschlagen und setzte die makroskopische Dehnung mit der Gitterdehnung gleich. Im Jahr 1961 entwickelte der deutsche Wissenschaftler Macherauch die Methode weiter2ψ-Methode, die auf der Idee von Akchenov beruht und die Messung von Eigenspannungen durch Röntgenbeugung zu einer zuverlässigen und weit verbreiteten Technologie macht.
In den letzten 60 Jahren hat sich die Röntgenbeugung zu mehreren verschiedenen Messmethoden entwickelt, wobei die2Die ψ-Methode und die cosα-Methode sind die beiden wichtigsten derzeit verwendeten Methoden.
Um die Röntgenbeugungstechnik zur Messung von Eigenspannungen zu beherrschen, ist es wichtig, ihre verschiedenen Methoden zu verstehen.
(1) Die Methoden zur Messung von Eigenspannungen mittels Röntgenbeugung können in zwei Hauptansätze unterteilt werden: die sin2ψ-Methode und die cosα-Methode.
(2) Die Sünde2Die ψ-Methode lässt sich anhand der Berechnungsmethode für die Eigenspannung in die 2θ-Methode, die d-Wert-Methode und die Dehnungsmethode unterteilen.
(3) Ausgehend von der geometrischen Beziehung zwischen ψ und 2θ ist der sin2Die ψ-Methode kann in zwei Arten unterteilt werden: die Co-Tilt-Methode und die Roll-Methode.
(4) Das Messverfahren kann auch nach dem Abtastmodus der Röntgenröhre und der Gegenröhre unterschieden werden, und zwar in das feste ψ0-Verfahren und das feste ψ-Verfahren.
(5) Innerhalb der Walzenmethode gibt es drei Unterkategorien: die Standard-Walzenmethode, die modifizierte Walzenmethode und die Walzenfixierungsmethode ψ.
(6) Die positive und negative ψ-Messmethode wird zur Bestimmung der Scherspannung τφ verwendet.
(7) Die Röntgenbeugung wird in der Regel zur Messung der Spannung in einer bestimmten Richtung an einem bestimmten Punkt verwendet, aber es gibt auch Verfahren zur Messung der Hauptspannung an einem Punkt.
(8) Die Schwingungsmethode kann in mehrere Unterkategorien unterteilt werden: die ψ0-Schwingungsmethode, die ψ-Schwingungsmethode, die Debye-Ring-Schwingungsmethode, die φ-Winkel-Schwingungsmethode und die X/Y-Verschiebungsmethode.
(9) In Bezug auf die Beugungsgeometrie gibt es drei Ansätze: die Fokussierungsmethode, die Quasi-Fokussierungsmethode und die Parallelstrahlmethode.
Die Spannung wird durch die Dehnung bestimmt. Bei polykristallinen Werkstoffen wird die Eigenspannung anhand des statistischen Ergebnisses der Gitterdehnung in dem betreffenden Bereich geschätzt.
So kann die Eigenspannung durch Messung der Gitterdehnung mit Hilfe der Röntgenbeugungstechnik bestimmt werden.
Die Eigenspannung des Materials spiegelt die Makrodehnung wider.
Die Makrodehnung ist gleichbedeutend mit der Gitterdehnung.
Die Gitterdehnung ist die relative Veränderung des Abstandes zwischen den Kristallebenen, die mit einem Beugungsgerät auf der Grundlage des Bragg-Gesetzes berechnet werden kann.
Dies ist eine Zusammenfassung der Röntgenbeugungsmethode zur Messung von Eigenspannungen.
Wenn ein Polykristall einem Röntgenstrahl mit einer bestimmten Wellenlänge (λ) ausgesetzt wird, wird die maximale Intensität der reflektierten Röntgenstrahlung (d. h. der Beugungspeak) bei einem bestimmten Beugungswinkel (2θ) beobachtet, wie in Abbildung 1 dargestellt. Dieses Phänomen wird als Röntgenbeugung bezeichnet.
Die Beziehung zwischen der Röntgenwellenlänge (λ), dem Kristallebenenabstand (d) und dem Bragg-Winkel (θ) wird durch die folgende Gleichung (1) beschrieben.

Bei der Röntgenbeugungsanalyse von Eigenspannungen wird das geeignete Zielmaterial für die Röntgenröhre ausgewählt, um die geeignete Wellenlänge (λ) zu bestimmen. Der Beugungswinkel (2θ) wird dann mit einem Beugungsgerät gemessen. Auf der Grundlage der Messung kann der Kristallebenenabstand (d) der betreffenden Kristallebene berechnet werden.

Abb. 1 Geometrie der Röntgenbeugung
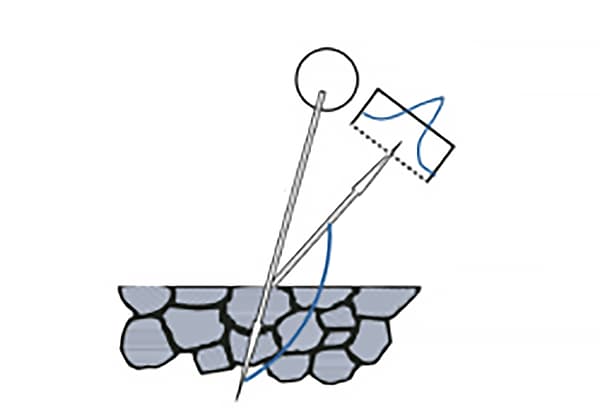
Gemäß dem Reflexionsgesetz der Optik muss die Normale der an der Beugung beteiligten Kristallebene auf der Winkelhalbierenden zwischen dem einfallenden und dem reflektierten Strahl liegen, wie in Abbildung 2 dargestellt.
Der Winkel zwischen der Normalen der Beugungskristallebene und der Normalen der Probenoberfläche wird als Azimutwinkel der Normalen der Beugungskristallebene bezeichnet und üblicherweise durch ψ dargestellt.

Abb. 2 Schematisches Diagramm der Röntgenbeugung Kristallebene Azimut ψ
Mit dem Braggschen Gesetz lässt sich der Abstand (dψ) von Kristallebenen in einer bestimmten Ausrichtung (ψ) bestimmen.
Wenn der Abstand (d0) der Kristallebenen im spannungsfreien Zustand bekannt ist, kann die Gitterdehnung (εψ) in der gewünschten Orientierung berechnet werden.
S1, S2 und S3 sind die Achsen der Probenoberfläche, und S1 wird vom Forscher definiert.
Abbildung 3 zeigt das Koordinatensystem, das für die Messung der Eigenspannung durch Röntgenbeugung verwendet wird.

Abb. 3 Koordinatensystem für die Röntgenbeugungsspannungsmessung
Nach dem verallgemeinerten Hooke'schen Gesetz werden die Dehnungen dieser Kristallebenen durch den Spannungstensor im Punkt O beeinflusst und sind eng mit dem Sinus und Kosinus von φ und ψ, dem Elastizitätsmodul des Materials und der Poissonzahl verbunden.
Somit ist es möglich, die dreidimensionale Spannung im Punkt O zu bestimmen, einschließlich der Spannung (σφ).
Der Ausdruck für die Dehnung in OP-Richtung kann aus der Elastizitätstheorie abgeleitet werden.
Bei den meisten Werkstoffen und Bauteilen beträgt die Eindringtiefe von Röntgenstrahlen nur wenige Mikrometer bis zu einigen Dutzend Mikrometern, so dass üblicherweise angenommen wird, dass σ33=0.
Daher wird die Dehnung in OP-Richtung durch Gleichung (2) dargestellt.


Die Sünde2Die Formel für die ψ-Methode wird auf der Grundlage des Braggschen Gesetzes und der elastischen Theorie abgeleitet.
Bei den in der Elastizitätstheorie betrachteten Objekten wird davon ausgegangen, dass es sich um homogene, kontinuierliche und isotrope Medien handelt.
Diese Annahme gilt jedoch nur für polykristalline metallische Werkstoffe wenn die Körnung fein ist und keine Textur vorhanden ist.
Abb. 4 zeigt die funktionale Beziehungskurve von εn und Sünde2ψ für isotrope Werkstoffe, Werkstoffe mit Spannungsgradient oder Zusammensetzungsgradient, Werkstoffe mit Scherspannung und anisotrope Werkstoffe mit Textur.

Wie in Abb. 4c) gezeigt, kann die Schubspannung τ13≠ 0, τ23≠0 und sin2ψ-Kurve haben ± ψ-Verzweigung, σφ und τφ kann durch Verwendung der gemessenen Dehnungsdaten ε erhalten werden﹢ψ und ε-ψ über eine Reihe von ± ψ-Winkeln, wie in Formel (4) und Formel (5) dargestellt.

Es ist wichtig zu wissen, dass die Sünde2ψ-Kurve in Abbildung 4c) ist eine ±ψ-Bifurkation unwahrscheinlich.
Der Grund dafür ist, dass die für die Beugung verwendeten Röntgenstrahlen nur eine begrenzte Eindringtiefe in das geprüfte Material haben, in der Regel nur wenige Mikrometer bis einige zehn Mikrometer.
Folglich können die Spannungskomponenten senkrecht zur Materialoberfläche als Null angesehen werden.
Nur wenn die Hauptspannungsebene unter der Bedingung einer besonderen Bearbeitung (z. B. starkes und großes Schleifen) von der Oberfläche der Probe abweicht, kann τ13≠0 und τ23≠0 auftreten.
Die ±ψ-Bifurkation kommt nicht häufig vor, und der Anpassungskurve fehlt oft das Attribut Ellipse. Dies ist weitgehend auf den systematischen Fehler im ±ψ-Mechanismus des Goniometers zurückzuführen. Daher muss die Bedeutung der Ellipsenanpassung nicht übermäßig betont werden.
Zusammenfassend lässt sich sagen, dass das praktische und umsetzbare Verfahren zur Bestimmung der Eigenspannung durch Röntgenbeugung die Auswahl einiger ψ-Winkel (oder mehrerer Paare von ±ψ-Winkeln) und die Messung des entsprechenden Beugungswinkels (2θφψ) mit anschließender Berechnung umfasst.
Wissenschaftler haben verschiedene Methoden entwickelt, um die räumliche geometrische Beziehung zwischen der ψ-Ebene und der 2θ-Ebene zu bestimmen, die Beugungskurve zu ermitteln und Berechnungen durchzuführen.
Der Beugungswinkel 2θφψ wird mit dem Röntgenbeugungsgerät gemessen, und der entsprechende Kristallebenenabstand wird berechnet als dφψ nach dem Bragg-Gesetz, dann ist die Gitterdehnung εφψ kann durch den Abstand zwischen den Kristallebenen ausgedrückt werden, wie in Formel (6) gezeigt.

Die wahre Dehnung wird direkt in Gleichung (3), Gleichung (4) und Gleichung (5) eingesetzt, um die Spannung zu berechnen, die der Ausdruck für die wahre Dehnung ist.
Die Methode der echten Dehnung wird angewandt, und die genauen Werte von d0 und θ0 sind nicht erforderlich.
In den meisten Fällen hat die Methode der echten Dehnung erhebliche Vorteile.
Zur Berechnung der Dehnung können auch Näherungsgleichungen verwendet werden, wie in Gl. (7) und Gl. (8) dargestellt.

Die Berechnungsformel der 2θ-Methode ist in Gleichung (9) dargestellt.

Dabei ist K die Spannungskonstante, deren Berechnungsformel in Gleichung (10) dargestellt ist.

Dabei ist ν die Poissonzahl des Materials.
Bei einigen Materialien ist θ0 variiert stark mit der chemischen Zusammensetzung, und die Ergebnisse weisen große Abweichungen auf, wenn die Spannungskonstante verwendet wird.
Die Methode der echten Dehnung wurde in die EU-Norm EN 15305-2008 Zerstörungsfreie Prüfung - Prüfverfahren für die Eigenspannungsanalyse mittels Röntgenbeugung und GB/T 7704-2017 Zerstörungsfreie Prüfung - Röntgenspannungsmessverfahren aufgenommen.
Das XL-640 Haushaltsspannungsmessgerät listet die Methode der echten Dehnung als Standardmethode für die Spannungsberechnung auf, und die 2θ-Methode kann für die Berechnung ausgewählt werden.
Die koplanare Methode ist eine Messmethode, bei der die 2θ-Ebene mit der ψ-Ebene (Spannungsrichtungsebene) zusammenfällt, wie in Abb. 5 dargestellt.

Abb. 5 Geometrisches Diagramm des gleichen Kippverfahrens
Mit der gleichen Neigungsmethode wird der Röntgeneinfallswinkel ψ0 dominiert, während der Winkel ψ berechnet werden kann, wie in Gleichung (11) und Gleichung (12) gezeigt.

Bei der Belastungsprüfung des tatsächlichen Werkstücks, wenn sich der Prüfpunkt in einer ähnlich flachen Nut befindet, ist der Prüfraum des Goniometers begrenzt, so dass die gleiche Neigungsmethode besser geeignet ist.
Die Rollmethode ist eine Messmethode, bei der die 2θ-Ebene und die ψ-Ebene (Spannungsrichtungsebene) senkrecht zueinander stehen, wie in Abb. 6 dargestellt.

Abb. 6 Geometrisches Diagramm der Rollmethode
Das Hauptmerkmal der Roll-Methode (χ-Methode) ist der kleine Absorptionsfaktor des Beugungspeaks, der zu einer höheren Messgenauigkeit beiträgt.
Die Bereiche 2θ und ψ können bei Bedarf vollständig erweitert werden. Bei bestimmten Materialien können Diffraktionsstrahlen mit niedrigen Peakpositionen (z. B. Peaks unter 145°) für die Spannungsmessung verwendet werden.
Allerdings stehen die 2θ-Ebene und die ψ-Ebene bei dieser Methode senkrecht zueinander, so dass ein dreidimensionaler Raum erforderlich ist, was die Anwendung bei der Messung enger Räume erschwert.
Das Stressmessgerät eines ausländischen Unternehmens arbeitet mit einer modifizierten Roll-Methode mit Doppeldetektoren, wie in Abbildung 7 dargestellt. Der geometrische Aufbau des Geräts ist in der Abbildung dargestellt.

Abb. 7 Geometrisches Diagramm der modifizierten Rollmethode
Bereits im Januar 1977 schlug Li Jiabao, Institut für Metalle, Chinesische Akademie der Wissenschaften, diese Prüfmethode und Berechnungsformel vor, wie in Gl. (13) und Gl. (14) dargestellt.
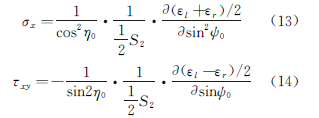
Die Walzenmethode kann in zwei Kategorien unterteilt werden: die feste ψ0-Methode und die feste ψ-Methode.
Die feste ψ-Methode gilt als besser als die feste ψ0-Methode, da sie genauere Grundsätze und bessere Ergebnisse in der Praxis liefert.
Durch die Kombination dieser beiden Methoden, der rollenfixierten ψ-Methode, kann der Absorptionsfaktor gleich 1 sein.
Das bedeutet, dass der Beugungspeak am hinteren Boden nicht kippt, die Peakform symmetrisch bleibt und die Peakform und -intensität unverändert bleibt, auch wenn sich der Winkel ψ ändert, solange keine Textur vorhanden ist.
Diese Eigenschaft erhöht die Messgenauigkeit erheblich und macht die rollenfixierte ψ-Methode zu einem idealen Messverfahren.
Bei der Schwenkmethode wird jeder eingestellte Winkel ψ (oder ψ0-Winkel) als Mittelpunkt verwendet, und die Röntgenröhre und der Detektor schwingen in einem bestimmten Winkel (±Δψ oder ±Δψ0) nach links und rechts.
Diese Methode erhöht die Anzahl der Körner, die an der Beugung teilnehmen, was sie zu einer effektiven Methode zur Messung der Spannung in grobkörnigen Materialien macht.
Andere Schwungmethoden, wie die φ-Winkel-Schwungmethode und die X/Y-Translationsschwungmethode, können ebenfalls verwendet werden, und verschiedene Schwungmethoden können zu Testzwecken sogar kombiniert werden.
Im Jahr 2012 stellte das japanische Unternehmen PULSTEC ein Stressmessgerät vor, das zum ersten Mal eine zweidimensionale Detektortechnologie verwendet.
Dieses Gerät arbeitet mit einem einzigen Einfallsmodus und einem zweidimensionalen Detektor zur Erfassung von Röntgenbeugungsdaten, so dass es schnell Debye-Ring-Daten am Prüfpunkt erfassen kann.
Da der Winkel ψ, der von der Normalen der Kristallfläche und der Normalen der Probenoberfläche gebildet wird, nicht für jeden Punkt des Debye-Rings in derselben Ebene liegt, ist der sin2ψ-Methode kann nicht zur Berechnung der Spannung verwendet werden. Stattdessen wird die Winkel-α- oder cosα-Methode angewandt (wie in Abbildung 8 dargestellt).
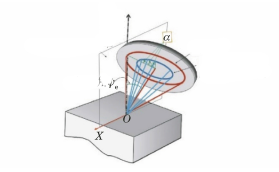
Abb. 8 Geometrisches Diagramm der Methode cosα
Diese Prüfmethode ist ideal für die Messung von Oberflächenspannungen in großen Stahlkonstruktionen.
Bei der Prüfung von grobkörnigen Materialien oder Materialien mit Textur stößt sie jedoch an ihre Grenzen.
Die cosα-Methode beruht auf den Prinzipien der Elastizität, wie die Gleichungen (15) und (16) zeigen.

Abbildung 9 zeigt den maximalen Winkelbereich ψ, der mit einem "vollen Zweipunktdetektor" (mit einem Einfallswinkel von 45°) erfasst werden kann.
Der Winkel α liegt auf der Debye-Ring-Ebene, die der Mittelpunktswinkel jedes Punktes auf dem Debye-Ring ist.

Abb. 9 Lage der Datenpunkte der Methode sin2ψ in s-Kurve
Beide Methoden zur Messung von Eigenspannungen mittels Röntgenbeugung beruhen auf demselben mechanischen Prinzip.
Der Dehnungstensor kann in den Raumwinkel transformiert werden, und der in der cosα-Methode verwendete α-Winkel kann vollständig in den ψ-Winkel umgewandelt werden.
Die cosα-Methode ist im Wesentlichen eine Annäherung an die sin2ψ-Methode.
Normalerweise gelten warmgewalzte Stahlbleche als texturfrei. Allerdings sind einige Teile der Stahlplatte kann aufgrund verschiedener Faktoren eine Textur aufweisen.
Trotzdem entscheiden sich viele Anwender in solchen Fällen für die Messung der Eigenspannung mittels Röntgenbeugung.
Wird zum Beispiel ein warmgewalztes Stahlblech mit Textur ausgewählt, so sind die Prüfbedingungen und Ergebnisse in Tabelle 1 und Tabelle 2 zu sehen. Der Prüfbericht für die Eigenspannungsmessung am Punkt Z (0) mit jedem Gerät ist in den Abbildungen 10-13 dargestellt.
Tabelle 1 Prüfparameter für die Messung der Eigenspannung von heißen Gewalzter Stahl Platte mit verschiedenen Spannungsinstrumenten
| Gerätetyp | μ-X360S | PROTO LXRD | X-RAYBOT | XL-640 |
| Prüfverfahren | cosα | Sünde2ψ | Sünde2ψ | Sünde2ψ |
| Spannung/kV | 20 | 30 | 20 | 25 |
| Stromstärke/mA | 1 | 25 | 1 | 6 |
| Beleuchteter Punkt/mm | 1 | 1 | 1 | 1 |
| ψ Bereich/(°) | – | -35~35 | -40~40 | 0~45 |
| Methode zur Berechnung der Dehnung | – | D-Wert-Methode | Methode der Dehnung | Methode der Dehnung |
| Peak-Bestimmungsmethode | – | PersonVII | Mittlerer Punkt | Methode der Kreuzkorrelation |
| Eigenspannung/MPa | 78 | 213.6 | 144 | 113 |
Tabelle 2 Eigenspannung von warmgewalzten Stahlplatten, gemessen mit verschiedenen Spannungsmessgeräten
| Prüfpunkt | μ-X360S | PROTO LXRD | X-RAYBOT | XL-640 |
| Z(5) | 29,47 | 122 | 107 | 77 |
| Z(4) | 37,52 | 135 | 112 | 70 |
| Z(3) | 74,70 | 104 | 95 | 67 |
| Z(2) | 38,28 | 153 | 99 | 134 |
| Z(1) | 37,64 | 166 | 122 | 101 |
| Z(0) | 64,78 | 144 | 213 | 113 |
| Z(-1) | 72,71 | 138 | 97 | 139 |
| Z(-2) | 62,52 | 134 | 83 | 145 |
| Z(-3) | 75,70 | 120 | 93 | 153 |
| Z(-4) | 63,56 | 114 | 80 | 148 |
| Z(-5) | 79,27 | 94 | 93 | 152 |

Abb. 10 Debye-Ring am Punkt Z (0), gemessen mit einem Spannungsmessgerät vom Typ μ-X360S

Abb. 11 2θ-sin2ψ-Kurve von Z (0), gemessen mit dem PROTO LXRD-Spannungsmesser

Abb. 12 2θ-sin2ψ Kurve des Messpunktes Z (0) mit X-RAYBOT Spannungsmessgerät

Abb. 13 ε-sin2ψ-Kurve von Z (0) gemessen mit XL-640 Spannungsmessgerät
Die mit der c-Methode gemessene Eigenspannung ist kleiner als die mit der s-Methode gemessene.
Für den Prüfpunkt Z (0) wird das Spannungsmessgerät verwendet. Nach dem Prinzip des gleichen Abstandes von sin2ψ, 8 ψ-Winkel werden im Bereich von 0°~45° gewählt.
Die Ergebnisse sind in Abb. 14-15 dargestellt. Es ist zu erkennen, dass die sin2Die ψ-Kurve des Materials weist aufgrund der Textur einen "Schock"-Typ auf.
Die Ordinate der Sünde2ψ-Kurve in Abb. 13 ist die Dehnung ε. Nachdem die Ordinate auf 2θ geändert wurde, wird eine lineare Anpassung durchgeführt. Die Ergebnisse sind in Abb. 14 dargestellt.
Die Steigung M der Anpassungsgeraden beträgt -0,355, und die Eigenspannung σ beträgt 113 MPa.

Abb. 14 Anpassungsergebnisse von 2θ-sin2ψ-Kurve, gemessen mit dem XL-640-Spannungsmesser am Punkt Z (0)
Der vom μ-X360S-Spannungsmessgerät ausgewählte ψ-Bereich entspricht den ersten beiden 2θ-Werten der Abschirmung, und dann wird die Geradenanpassung durchgeführt. Die Ergebnisse sind in Abb. 15 dargestellt.

Abb. 15 Ergebnisse der Anpassung von 2θ-sin2ψ-Kurve von Z (0), gemessen mit einem Spannungsmessgerät vom Typ μ-X360S
Verwenden Sie das PROTO LXRD-Spannungsmessgerät, um den ausgewählten ψ-Bereich zu testen, schirmen Sie die letzten drei 2θ-Werte in Abb. 14 ab und führen Sie dann eine lineare Anpassung durch. Die Ergebnisse sind in Abb.16 dargestellt.

Abb. 16 Anpassungsergebnisse von 2θ-sin2ψ-Kurve, gemessen mit dem PROTO LXRD-Spannungsmesser am Punkt Z (0)
Aus Abbildung 12 ist ersichtlich, dass der maximale sin2Der ψ-Wert des Punktes Z (0) beträgt 0,4 bei Verwendung des X-RAYBOT-Spannungsmessers.
Schirmen Sie entsprechend dem gewählten ψ-Bereich die letzten beiden 2θ-Werte in Abb. 14 ab und führen Sie dann eine lineare Anpassung durch. Die Ergebnisse sind in Abb. 17 dargestellt.

Abb. 17 Ergebnisse der Anpassung von 2θ-sin2ψ Kurve von Z (0), gemessen mit dem X-RAYBOT Spannungsprüfer
Aufgrund der Beschaffenheit des Materials, seiner Sünde2ψ-Kurve ist oszillierend.
Der gewählte ψ-Winkelbereich ist unterschiedlich, was zu Unterschieden in der Steigung und den Eigenspannungswerten führt, die aus der Anpassungsgeraden ermittelt werden.
Bei Materialien mit unbekannter Textur und grobem Korn ist es nicht ratsam, einen engen ψ-Bereich und eine geringe Anzahl von ψ-Stationen für die Eigenspannungsmessung zu wählen, da dies zu erheblichen Messfehlern führen kann.
Die lineare Anpassung ist möglicherweise nicht für Materialien mit strukturierter Oberfläche geeignet.2ψ-Kurven, die oszillierend sind.
Während des Messvorgangs wird häufig eine lineare Anpassung verwendet, um die durch Vibrationen und Messfehler verursachten Schwankungen zu mildern.
Es ist möglicherweise nicht möglich, einen ψ-Winkel von 45° zu erreichen, da dieser durch die Eindringtiefe beeinflusst werden könnte. Ein größerer Winkel führt wahrscheinlich zu genaueren Ergebnissen, vorausgesetzt, die Eindringtiefe kann vernachlässigt werden.
Bei Materialien mit grober Körnung oder Textur sollte der ψ-Winkelbereich so weit wie möglich ausgedehnt werden, um die Auswirkungen der nichtlinearen ε-sin2ψ-Verteilung. Dies kann durch Messung beider ±ψ-Winkel erreicht werden.
Die Genauigkeit der angepassten Geraden kann verbessert werden, indem die Methode der kleinsten Quadrate für die Regressionsanpassung verwendet und sowohl der ψ-Bereich als auch die Anzahl der ψ-Stationen erhöht wird. Dies wird zu zuverlässigeren Testwerten führen.
Die Messgenauigkeit kann auch durch eine Vergrößerung der Röntgenbelichtungsfläche oder durch eine Erhöhung der Anzahl der Beugungskörner, die an der Swing-Methode teilnehmen, verbessert werden.
(1) Die Sünde2Die ψ-Methode kann zur Bestimmung der Eigenspannung mit verbesserter Genauigkeit verwendet werden, indem der ψ-Bereich vergrößert und mehr ψ-Stationen ausgewählt werden. Diese Methode hat jedoch ihre Grenzen, da es sich um eine Einzelbelichtung handelt, die zu großen Messfehlern führen kann, wenn der Bereich von ψ nicht ausreicht.
(2) Bei den Messmethoden, die die Sinuskurve2ψ Grundsätzlich ist die Rollmethode der Kippmethode überlegen. Es wird empfohlen, die Rollmethode anzuwenden, wenn die Platzverhältnisse an der Messstelle dies zulassen. Für die Messung von Eigenspannungen in Nuten bestimmter Bauteile wird in der Regel die Co-Inklinationsmethode verwendet.
(3) Die Methode der echten Dehnung ist eine bevorzugte Methode zur Berechnung der Eigenspannung.
(4) Die sin2ψ-Methode gilt als Standardmethode für diesen Zweck. Um die genauesten Ergebnisse zu erhalten, sollte der Winkel ψ mit der Methode sin2ψ-Wert-Bisektionsmethode, und es sollten so viele ψ-Winkel wie möglich gemessen werden.