Was wäre, wenn Sie die komplizierten Z-förmigen Biegungen in Metall mit Präzision und Leichtigkeit perfektionieren könnten? Dieser Artikel befasst sich mit den strukturellen Feinheiten des Z-förmigen Biegens und der Umformmatrize und beleuchtet die wichtigsten Techniken und Berechnungen. Sie erfahren, wie Sie Biegeprozesse optimieren, die Spannungsverteilung verstehen und Verbundwerkzeuge für verschiedene Blechmaterialien einsetzen können. Egal, ob Sie Ingenieur oder Maschinenbauer sind, gewinnen Sie Erkenntnisse, die die Produktion rationalisieren und die Genauigkeit Ihrer Metallbearbeitungsprojekte verbessern. Tauchen Sie ein, um die Komplexität des Z-förmigen Biegens zu meistern und Ihren Arbeitsablauf zu verbessern.
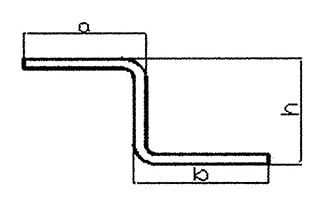
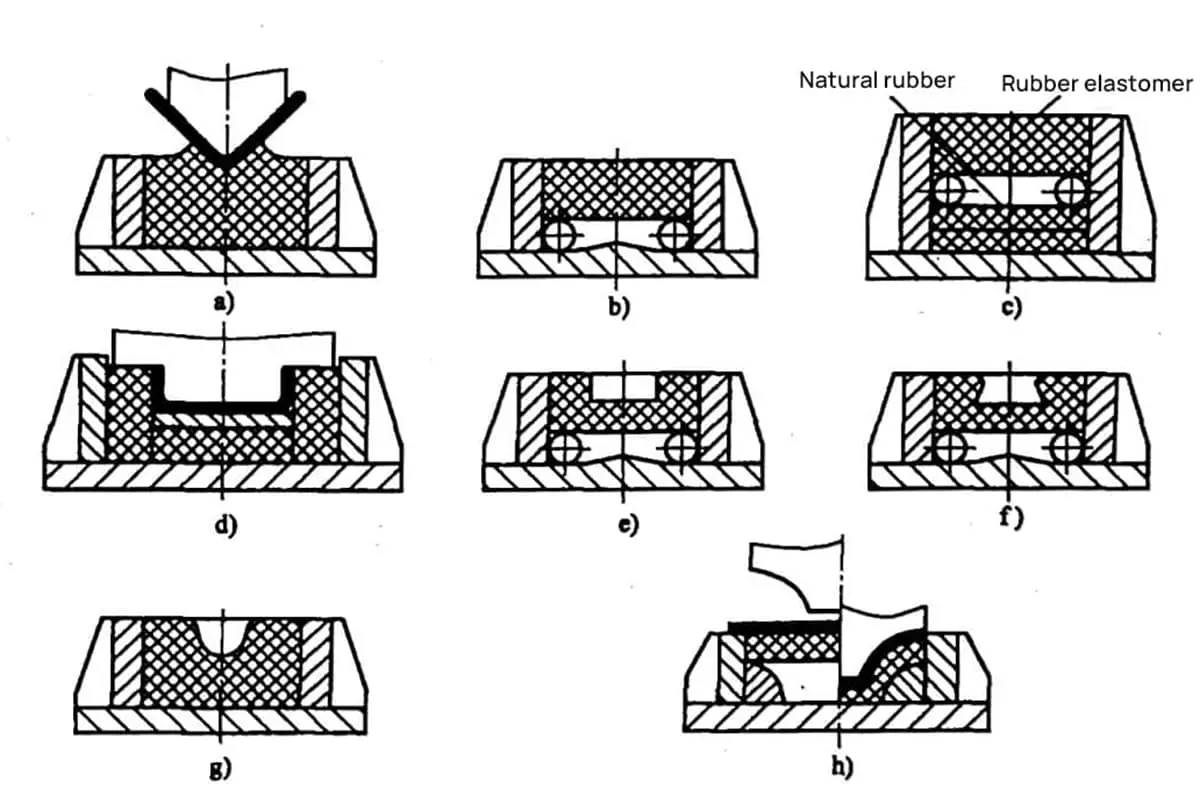
Das in Abbildung 1 dargestellte Z-förmige Biegeteil ist ein in der Produktion häufig anzutreffendes Teil. Die Größe von h wird durch das Unterwerkzeug begrenzt, wobei die Mindestgröße, die mit dem vorhandenen Unterwerkzeug gebogen werden kann, in Tabelle 1 angegeben ist.
Tabelle 1 Mindestgröße Biegen
| Dicke der Platte | 1 | 1.5 | 2 | 2.5 | 3 |
| Mindestgröße | 7 | 9.5 | 14 | 16 | 18 |
Wenn es in der praktischen Produktion zahlreiche Z-förmige Biegestempel gibt, die kleiner als die genannte Größe sind, wäre die Konstruktion eines zusammengesetzten Biegestempels erforderlich, um das Primärformverfahren durchzuführen. Diese Verbundmatrize kann zum Falten von Z-förmigen Biegestempeln verschiedener Größen auf unterschiedlichen Blechmaterialien verwendet werden.
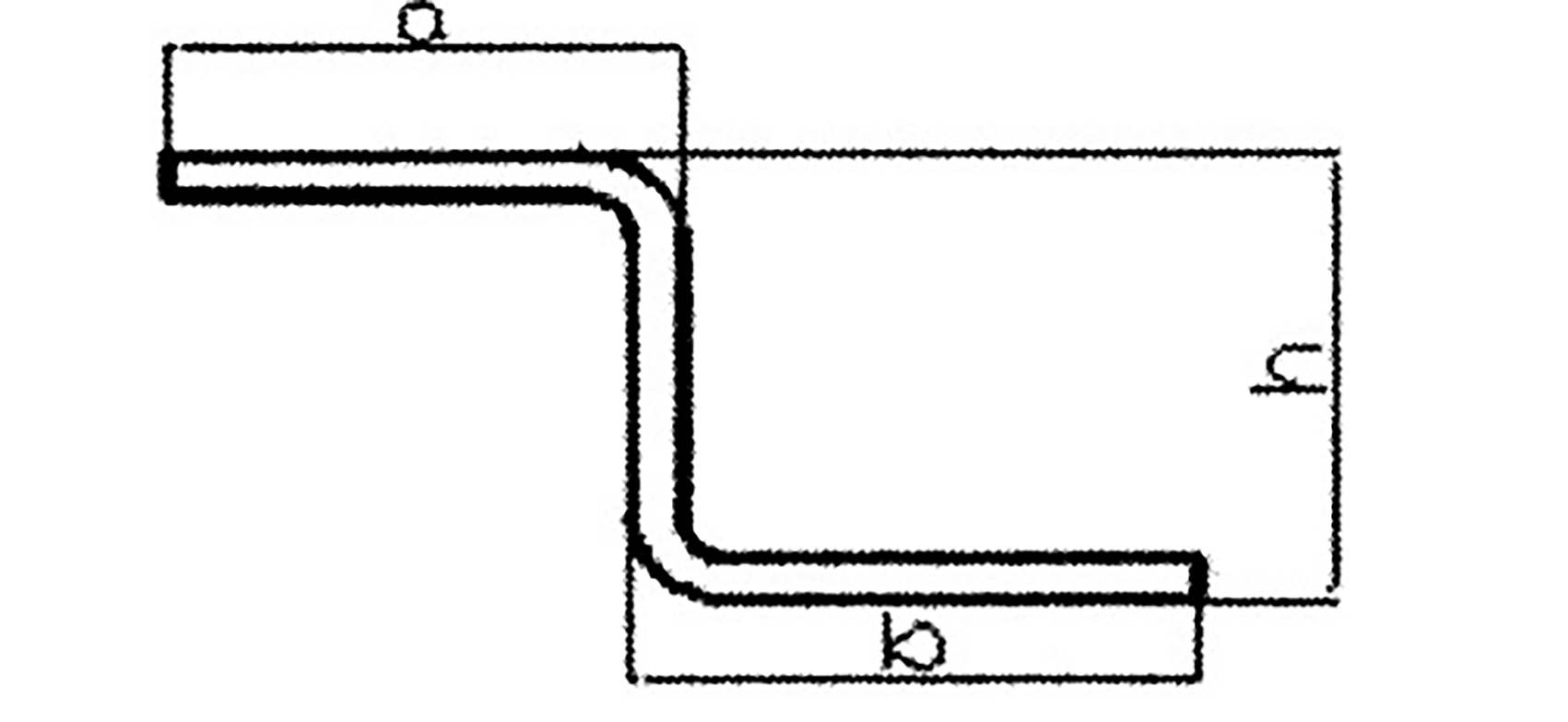
Abb. 1 Z-förmig Biegestempel
Abb. 2 Aktionskraftdiagramm
Wie in Abbildung 2 dargestellt, wird ein Feinblech auf Biegung beansprucht wird, erfährt sie ein Biegemoment, eine Querkraft und einen lokalen Druck. Die wichtigste Auswirkung der Biegeverformung ist jedoch das Biegemoment.
Die Einwirkung einer äußeren Kraft führt zu einer entsprechenden Verformung des Blechs, die auch das Auftreten einer inneren Kraft auslöst, die der Verformung entgegenwirkt. Die innere Kraft gleicht sich mit der äußeren Kraft aus und wird als Spannung gemessen, die die innere Kraft pro Flächeneinheit des Objekts darstellt. Je höher die äußere Kraft ist, desto größer sind die Spannung und die Verformung.
Wenn die äußere Spannung des Materials unter seiner Elastizitätsgrenze liegt, befindet sich das Blech in einem elastischen Verformungszustand. Nach dem Hooke'schen Gesetz ist die lineare Beziehung zwischen Spannung und Verformung im Querschnitt auf die lineare Änderung des Abstands zwischen der Verformung und der mittleren Schicht zurückzuführen (Verlängerung der äußeren Schicht und Verkürzung der inneren Schicht).
Wird die äußere Kraft weggenommen, kehrt das Blech in seine ursprüngliche Form zurück. Nimmt die äußere Kraft jedoch weiter zu, steigt der Verformungsgrad des Biegeteils weiter an, bis die durch die äußere Kraft verursachte Spannung die Streckgrenze des Materials erreicht, was zu einer plastischen Verformung des Außenmaterials führt.
Mit zunehmender äußerer Kraft schreitet die plastische Verformung von der Oberfläche zur Mitte hin fort. Sobald die äußere Kraft entfernt wird, verschwindet die elastische Verformung sofort, aber die plastische Verformung bleibt bestehen und führt zu einer dauerhaften Biegeverformung.
Übersteigt die durch die äußere Kraft verursachte Spannung die Festigkeitsgrenze des Materials, bricht das Blech durch plastische Verformung. Innere Verdichtung bei Blechbiegen führt ebenfalls zu einer plastischen Verformung, aber diese Art der plastischen Verformung erhöht die Spannung an der Oberfläche, ohne Schäden zu verursachen, und wird daher oft ignoriert.
Nun beobachten wir sorgfältig die plastische Biegeverformung.
Unter der Einwirkung des Biegemoments ergeben sich drei gleiche Linien auf dem Plattenquerschnitt: ab= a1b1 = a2b2.
Nach dem Biegen verkürzt sich die innere Schicht und die äußere Schicht verlängert sich, d. h. ab < a1b1 < a2b2.
Daher wird beim Biegen das innere Material zusammengedrückt und verkürzt, während das äußere Material gedehnt und verlängert wird.
Zwischen Zug und Druck gibt es eine Materialschicht, die weder gedehnt noch gestaucht wird und die als neutrale Schicht bezeichnet wird. Diese Schicht bleibt in ihrer Länge unverändert und wird weder gedehnt noch verkürzt.
Bei der Berechnung des Biegeteils wird dieses in mehrere geometrische Grundelemente unterteilt, darunter Geraden- und Bogensegmente. Die Länge jedes Elements wird einzeln berechnet, und die Gesamtlänge aller Elemente ist die entfaltete Länge des Biegeteils.
Das Z-förmige Biegeteil in Abbildung 1 kann in fünf Einheiten unterteilt werden, wie in Abbildung 2 dargestellt. Die Einheiten 1, 3 und 5 sind gerade Liniensegmente, während die Einheiten 2 und 4 Bogensegmente sind.
Wie bereits erwähnt, wird die Faserschicht mit konstanter Länge in der Mitte vor und nach der Biegung als neutrale Schicht bezeichnet. Bei der Berechnung der Ausdehnungslänge des Bogensegments wird eigentlich die Länge der neutralen Schicht des Bogensegments berechnet.
Die Position x der neutralen Schicht von der Innenseite des Lichtbogens (wie in Abbildung 3 dargestellt) wird in der Regel durch das Verhältnis r/t bestimmt.
x = kt
Wo:
Wo:
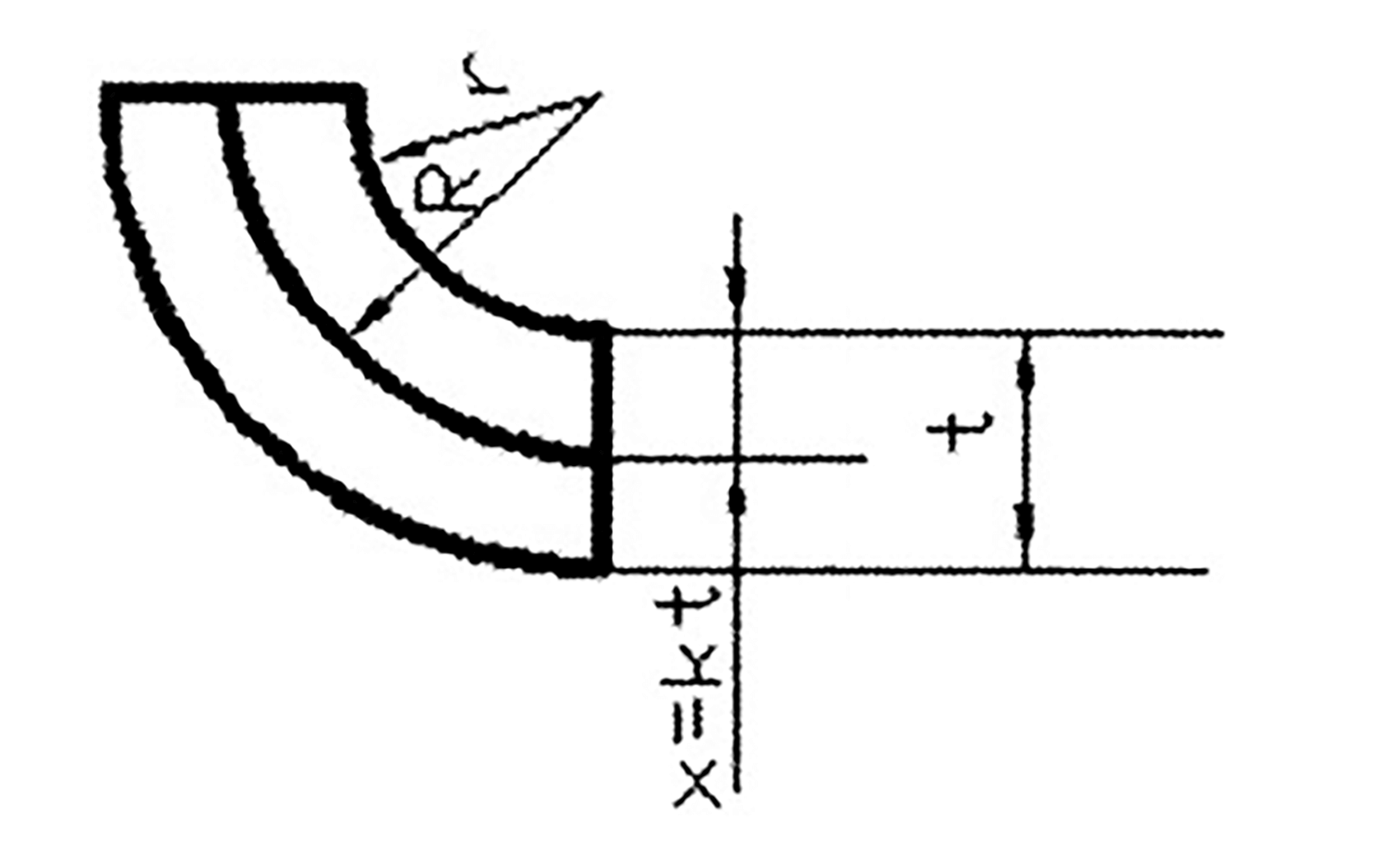
Abb. 3
Der Wert von k variiert mit dem Verhältnis von Innenradius zu Blechdicke, wie in Tabelle 2 dargestellt:
Tabelle 2
| r/t | 0.25 | 0.5 | 1 | 2 | 3 | 4 |
| k | 0.26 | 0.33 | 0.35 | 0.375 | 0.4 | 0.415 |
In der praktischen Produktion werden Stahlbleche meist in einem 90-Grad-Winkel gebogen.
Die Berechnung der Bogenlänge für 90-Grad-Biegungen mit unterschiedlichen r- und t-Werten kann in der Praxis anhand von Tabellen erfolgen.
Dieser Artikel konzentriert sich auf rechtwinklige 90-Grad-Biegungen, aber es ist nicht effizient, die Geraden- und Bogensegmente separat für Teile mit 90-Grad-Biegungen zu berechnen. Blechbiegen. Stattdessen werden sie wie in Abbildung 1 dargestellt markiert.
Bei der Berechnung des Abwicklungsmaterials können wir zur Vereinfachung des Berechnungsprozesses direkt die markierten Maße verwenden.
Gemäß Abbildung 1 wird die entwickelte Materiallänge berechnet:
L = a+b+h - 2x
Wo:
Tabelle 3 Gemeinsamer Biegekoeffizient x
| Dicke der Platte t | Inneres Biegeradius r | |||
|---|---|---|---|---|
| 1.0 | 1.5 | 2.0 | 2.5 | |
| 0.5 | 1.0 | 1.2 | 1.4 | 1.6 |
| 1 | 1.9 | 2.1 | 2.3 | 2.5 |
| 1.5 | 2.5 | 2.7 | 2.9 | 3.1 |
| 2.0 | 3.4 | 3.6 | 3.8 | 4.0 |
| 2.5 | 4.0 | 4.2 | 4.4 | 4.6 |
| 3 | 4.9 | 5.1 | 5.3 | 5.4 |
Diese einfache Matrize unterscheidet sich von der herkömmlichen Matrize.
Sie ist so konzipiert, dass sie einfach, schnell, leicht zu verarbeiten und unkompliziert zu formen ist. Sie ist zwar nicht so präzise wie eine herkömmliche Matrize, wird aber dennoch zur schnellen und genauen Verarbeitung von Produkten eingesetzt.
Das Umformdiagramm des Verbundwerkzeugs ist in Tabelle 3 dargestellt.
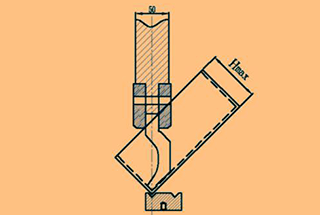
Verarbeitungsprinzip: Die Dicke der Dichtung wird so eingestellt, dass die gewünschte Breite der V-Nut im oberen und unteren Bereich erreicht wird. Untergesenkund eine einmalige Z-förmige Verarbeitung unter Druck durchzuführen.
Aufbau der Matrize: Die Z-förmige Biegematrize besteht aus einer oberen Matrize, einer unteren Matrize, einer Dichtung und einem Winkelprismenstahl.
Dicke der Dichtung: Der Abstandhalter ist aus 0.5 mm dick Stahl und wird gestapelt, um die erforderliche Dicke zu erreichen.
Prismenstahl: Ein rechteckiges Stahlstück in der Matrize, dessen vier Winkel zu Seiten von 0,5 mm, 1,0 mm, 2,0 mm und 4,0 mm abgeschrägt sind, wie in Tabelle 3 dargestellt.
Die spezielle einfache Matrize wird verwendet, um die gewünschte Breite der oberen und unteren V-Nut zu erreichen, indem die Größe des Winkelprismastahls und die Dicke der Dichtung angepasst werden, und dann die Z-Faltung in einer Presse durchgeführt wird.
Diese Methode wurde gewählt, weil sie die V-Nut vergrößern und die Faltenbildung verringern kann. Für unterschiedliche Blechdicken sind daher unterschiedliche Zinken erforderlich, wie in Tabelle 4 dargestellt.
Tabelle 4
| Dicke der Platte | t<0.8 | 0.8<t<1.0 | 1.0<t<1.2 | 1.2<t1.5 | t>1.5 |
| Zinken | 0.5 | 1.0 | 1,0 oder 2,0 | 2.0 | 4.0 |
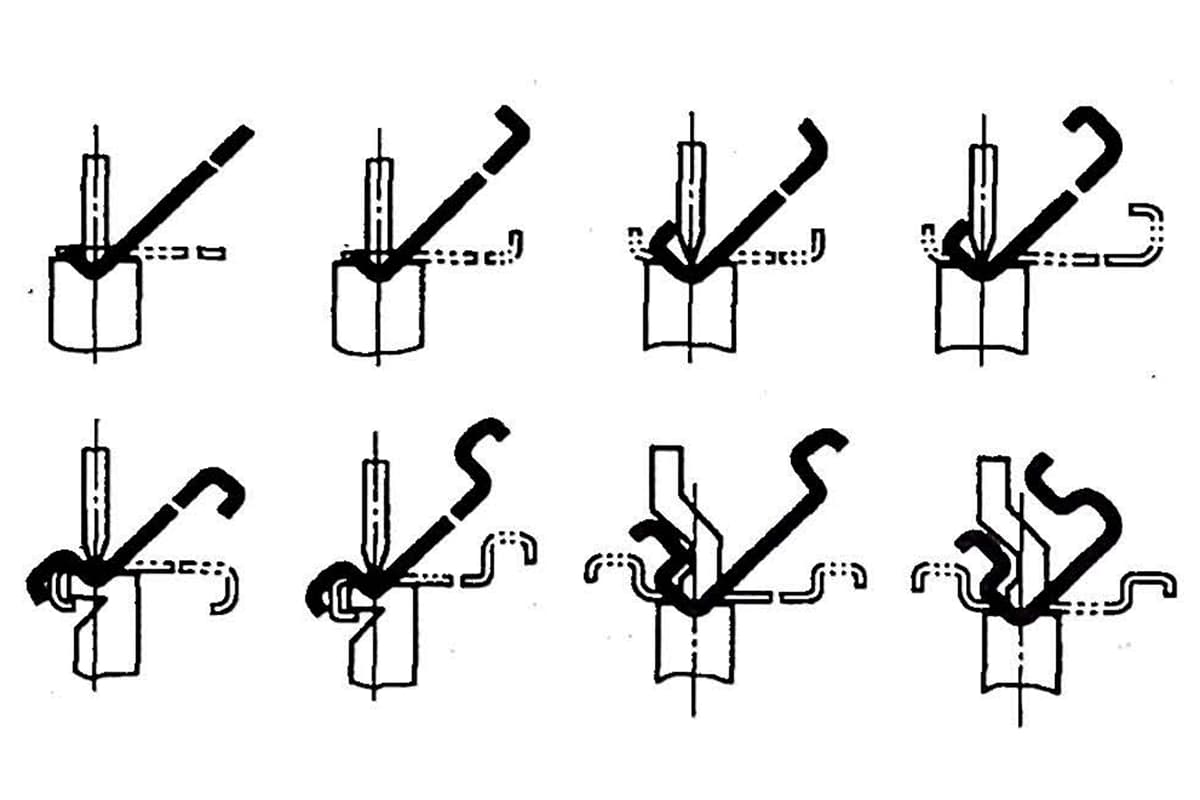
Fehlersuchmethode für Z-förmige Biegestempel:
1) Beide Falzungen des Z-Falzgerades sind 90°. Der Abstand zwischen den beiden Werkzeugspitzen beträgt: 1.414/2×h;
2) Wenn die Werkstückfalte zu tief ist, dann muss ein großer Winkel gewählt werden.
b: Bügeleisen; c: Winkel R erhöhen;
3) Wenn die Höhe erreicht ist, aber der Winkel größer als 90° ist, dann a: Exzentrizität der Matrize.
b: Erhöhen Sie die Dicke der Unterlegscheibe;
4) Wenn die beiden Seiten des Z-Falzes nicht parallel sind, kann dies durch Vergrößern oder Verkleinern der Dicke der Unterlegscheibe erreicht werden.
Wenn die obere Falte größer als 90° ist, muss die Dicke der unteren Matrizenscheibe erhöht werden; und wenn die untere Falte größer als 90° ist, muss die Dicke der oberen Matrizenscheibe erhöht werden.
Berechnungsmethode für die Z-Biegung:
Wenn h > normales Biegemaß ist, sollte es sich um zwei Falten entfalten.
L=a + b + h - 2x
Wo:
Wenn h < das normale Biegemaß ist, wird es durch einstufiges Umformen erweitert.
L = a + B + h - 1,5x
Wo:
Eine der empirischen Formeln in der Praxis ist, das 1,5-fache vom Gesamtmaß eines Formteils abzuziehen.