Calculadora del subsidio por flexión (en línea y gratuita)

Comprender el subsidio por flexión

La tolerancia de plegado es un concepto fundamental en la fabricación de chapa metálica, esencial para conseguir unas dimensiones exactas en las piezas metálicas plegadas. Tiene en cuenta el alargamiento del material que se produce durante el proceso de plegado, garantizando que las dimensiones finales de la pieza coincidan con las especificaciones de diseño.

Definición de compensación por flexión

La tolerancia de flexión se refiere a la longitud del eje neutro desde el principio hasta el final de la flexión. El eje neutro es una línea imaginaria dentro del material que no sufre compresión ni alargamiento durante el doblado. Este cálculo es crucial para determinar la disposición plana de una pieza de chapa metálica, ya que tiene en cuenta la deformación del material cuando se dobla.

Importancia en el diseño de chapa metálica

El cálculo preciso de la tolerancia de plegado es vital por varias razones. En primer lugar, garantiza que las dimensiones finales de la pieza doblada coincidan con las especificaciones del diseño. Además, ayuda a minimizar el desperdicio de material al predecir con exactitud la cantidad de material necesario. Esta reducción del desperdicio conlleva un ahorro de costes en el proceso de fabricación al reducir el riesgo de errores y repeticiones.

Factores que afectan al subsidio de curvatura

Hay varios factores que influyen en la tolerancia a la flexión. El grosor del material (T) desempeña un papel importante, ya que los materiales más gruesos tienen características de curvatura diferentes a las de los materiales más finos. El ángulo de curvatura (θ), que suele medirse como ángulo complementario, influye en el estiramiento del material. El radio interior (r) de la curva en el interior del material también influye en el cálculo. Por último, el factor K (K), una constante específica del material que representa la relación entre el grosor del material y el eje neutro, es crucial.

Fórmula de compensación por flexión

El margen de curvatura puede calcularse mediante la siguiente fórmula:

Dónde:

• ( BA ) es el margen de curvatura.
• ( θ ) es el ángulo de curvatura en grados.
• ( π/180 ) es un factor de conversión para convertir grados a radianes.
• ( r ) es el radio interior.
• ( K ) es el factor K.
• ( T ) es el espesor del material.

Ejemplo práctico

Consideremos una pieza de chapa con las siguientes propiedades:

• Ángulo de curvatura (( θ )) = 90°.
• Radio interior (( r )) = 5 mm
• Espesor del material (( T )) = 2 mm
• Factor K (( K )) = 0,33

Utilizando la fórmula del margen de plegado:

Este cálculo proporciona el margen de curvatura necesario para desarrollar con precisión el patrón plano de la pieza de chapa.

I. Calculadora de tolerancia a la flexión

Para los nuevos prensa plegadora Para los operarios que no estén familiarizados con los entresijos del cálculo de la sobremedida de curvatura, una calculadora de sobremedida de curvatura puede ser una herramienta inestimable. Esta calculadora simplifica el proceso, garantiza resultados precisos y hace que el trabajo diario sea más eficiente.

Las calculadoras de sobremedida de plegado en línea simplifican el proceso permitiendo a los usuarios introducir parámetros como el grosor del material, el ángulo de plegado, el radio interior y el factor K. Estas calculadoras calculan la sobremedida de plegado y, a veces, la deducción de plegado. A continuación, estas calculadoras calculan la tolerancia de curvatura y, en ocasiones, la deducción por curvatura, garantizando una fabricación precisa de la chapa metálica. Con estas herramientas, los fabricantes ahorran tiempo y reducen el riesgo de errores en sus cálculos.

Parámetros necesarios para el cálculo

Para utilizar eficazmente la calculadora de subsidios de curvatura, los operadores deben introducir los siguientes parámetros:

1. Material Grosor: El grosor del material influye en el radio de curvatura y en el margen de curvatura total.
2. Radio interior: El radio de la curva en la superficie interior del material.
3. Factor K: Relación que ayuda a determinar la ubicación del eje neutro durante la flexión.
4. Ángulo de curvatura: Ángulo con el que se dobla el material.

Calculadora relacionada:

• Calculadora del factor K
• Calculadora del factor Y
• Calculadora de deducción por flexión

Más información:

• ¿Cómo calcular la tolerancia a la flexión, la deducción por flexión y el factor K?

II. Qué es Compensación por flexión?

La sobremedida de plegado es la longitud adicional de material necesaria al plegar chapa metálica para conseguir las dimensiones finales deseadas tras el conformado. Compensa el estiramiento y la compresión que se producen en el material durante el proceso de plegado:

1. Propiedades del material: Los distintos materiales tienen diferente elasticidad y plasticidad, que afectan a cuánto se estira o comprime el material durante la flexión.
2. Grosor de la chapa: Las chapas más gruesas suelen requerir un mayor margen de curvatura que las chapas más finas del mismo material.
3. Método de doblado y utillaje: El tipo de proceso de curvado (por ejemplo, curvado por aire, bottoming, acuñado) y el diseño de la matriz de curvado pueden influir en la tolerancia de curvado.
4. Radio de curvatura interior: Un radio de curvatura interior más cerrado suele requerir una tolerancia de curvatura menor que un radio mayor.

Los valores de tolerancia de curvatura suelen determinarse mediante una combinación de datos empíricos, cálculos matemáticos y experiencia práctica. Los diseñadores e ingenieros de chapa con experiencia han desarrollado tablas y fórmulas de tolerancia de curvatura a lo largo de años de pruebas y verificaciones repetidas.

Utilizando la fórmula de sobremedida de plegado adecuada o consultando tablas de sobremedida de plegado fiables, los diseñadores pueden calcular con precisión las dimensiones del patrón plano de una pieza de chapa metálica que dará lugar a las dimensiones de plegado finales deseadas. Esto es crucial para crear patrones planos precisos y garantizar que la pieza doblada se ajuste y funcione según lo previsto.

III. Fórmula de compensación por flexión

Los cálculos de la sobremedida de plegado y la deducción de plegado son métodos esenciales utilizados para determinar la longitud de las materias primas de chapa metálica en su forma plana, garantizando que se alcance el tamaño deseado de la pieza plegada. Comprender estos cálculos es crucial para la precisión en la fabricación de chapa metálica.

Método de cálculo de la compensación por flexión:

La sobremedida de curvatura (BA) es la cantidad de material que se añade a la longitud total de la chapa plana para tener en cuenta el material que se utilizará en la curvatura. 

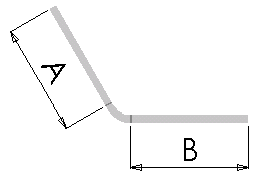
La siguiente ecuación se utiliza para determinar la longitud total de aplanado cuando se utiliza el valor de tolerancia de curvatura:

L_t = A + B + BA

Dónde:

• 𝐿_𝑡 es la longitud total plana.
• 𝐴 y 𝐵 son las longitudes de las dos secciones rectas de la chapa antes de la curva (como se muestra en la figura).
• 𝐵𝐴 es el valor de la tolerancia de flexión.

Método de cálculo de la deducción por flexión:

La deducción por plegado (BD) es la cantidad de material que se resta de la longitud total de la chapa plana para tener en cuenta el material que se utilizará en el plegado. 

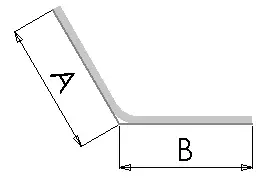
La siguiente ecuación se utiliza para determinar la longitud total de aplanado cuando se utiliza el valor de la deducción de curvatura:

L_t = A + B - BD

Dónde:

• 𝐿_𝑡 es la longitud total plana.
• 𝐴 y 𝐵 son las longitudes de las dos secciones rectas de la chapa antes de la curva (como se muestra en la figura).
• 𝐵𝐷 es el valor de la deducción por flexión.

Otros métodos de cálculo

Además de los métodos de tolerancia y deducción de curvatura, pueden utilizarse otras técnicas para determinar la longitud plana de las materias primas de chapa metálica. Entre ellas se incluyen:

• Tabla de tolerancia a la flexión: Una tabla precalculada que proporciona valores de tolerancia de curvatura para diversos materiales y ángulos de curvatura.
• Factor K: Relación que representa la ubicación del eje neutro en relación con el espesor del material. Se utiliza en cálculos de flexión más precisos.
• Cálculos de flexión: Para obtener resultados precisos, hay que tener en cuenta fórmulas y consideraciones más complejas, como las propiedades del material, el radio de curvatura y el grosor.

IV. Tabla de tolerancia a la flexión

1. Tabla de tolerancia a la flexión para SPCC (acero dulce)

2. Tabla de tolerancia de curvatura para SUS (acero inoxidable)

3. Tabla de tolerancia de curvatura para SPHC (acero inoxidable)

4. Tabla de tolerancia de curvatura para SECC (chapa de acero galvanizado)

5. Tabla de tolerancia de curvatura para chapa de aluminio

V. Importancia del factor K

Definición y función del factor K

El factor K es un coeficiente crucial en la fabricación de chapas metálicas, que representa la posición relativa del eje neutro dentro del espesor del material. El eje neutro es el plano imaginario dentro del material en el que no se produce compresión ni tensión durante el proceso de plegado. El factor K se calcula como la relación entre la distancia de la superficie interior al eje neutro y el grosor total del material. Comprender el factor K es esencial para calcular con precisión la tolerancia de plegado, garantizando la precisión de las dimensiones finales de las piezas plegadas.

Influencia en el subsidio de curvatura

El factor K influye directamente en la tolerancia de curvatura, que es la longitud adicional de material necesaria para acomodar la curva. La fórmula de la tolerancia de curvatura, que suele incluir el ángulo de curvatura, el radio interior, el grosor del material y el factor K, es la siguiente:

donde ( BA ) es la tolerancia de curvatura, ( θ ) es el ángulo de curvatura en radianes, ( r ) es el radio interior, ( K ) es el factor K y ( T ) es el espesor del material. Esta fórmula pone de relieve la importancia del factor K para garantizar que la tolerancia de curvatura se calcula con precisión, lo que es fundamental para conseguir unas dimensiones precisas de la pieza y reducir el desperdicio de material.

Dependencia de materiales y procesos

El factor K no es un valor constante y varía en función de varios factores, como las propiedades del material, el método de flexión, el radio de curvatura y el ángulo de curvatura. Diferentes materiales y condiciones de flexión darán lugar a diferentes valores del factor K, que suelen oscilar entre 0,3 y 0,5. Por ejemplo, un material muy dúctil puede tener un factor K diferente al de un material más quebradizo, lo que influye en el margen de curvatura y, en consecuencia, en las dimensiones finales de la pieza.

VI. Aplicación práctica: Guía paso a paso

Paso 1: Reunir los parámetros necesarios

Para calcular con precisión el margen y la deducción de curvatura, comience por recopilar los siguientes parámetros:

• Espesor del material (T): Mida el grosor de la chapa, normalmente en milímetros (mm) o pulgadas (pulg).
• Ángulo de curvatura (θ): Determine el ángulo en el que se doblará la chapa. Los ángulos más comunes son 90°, 120°, etc.
• Radio interior (IR): Mida el radio de la curva en el interior del material.
• Factor K (K): El factor K representa la relación entre el eje neutro del material y su grosor y es esencial para determinar cuánto material se necesita para una curva. Suele oscilar entre 0,3 y 0,5, en función de las propiedades y el grosor del material.

Paso 2: Calcular el margen de curvatura (BA)

La sobremedida de curvatura tiene en cuenta la longitud adicional de material necesaria para acomodar la curva. Utilice la fórmula de tolerancia de curvatura para determinar este valor:

Ejemplo de cálculo:

• Material: Acero dulce
• Espesor (T): 0,125 pulgadas
• Radio interior (IR): 0,250 pulgadas
• Ángulo de curvatura (θ): 90 grados
• Factor K (K): 0.42

1. Convertir el ángulo de curvatura en radianes:

2. Aplique la fórmula de tolerancia a la flexión:

Paso 3: Calcular el retranqueo exterior (OSSB)

A continuación, determine el retranqueo exterior, que es importante para calcular la deducción por curvatura. La fórmula para OSSB es:

Ejemplo de cálculo:

• Ángulo de curvatura (θ): 90 grados
• Espesor del material (T): 0,125 pulgadas
• Radio interior (IR): 0,250 pulgadas

Convertir Ángulo de Curvatura a Radianes:

Aplique la fórmula del retranqueo exterior:

Paso 4: Calcular la deducción por curvatura (BD)

Por último, utilice el retranqueo exterior y el margen de curvatura para determinar la deducción de curvatura, que es crucial para conseguir dimensiones precisas en la fabricación de chapa metálica:

Ejemplo de cálculo:

• Retroceso exterior (OSSB): 0,375 pulgadas
• Tolerancia de curvatura (BA): 0,475 pulgadas

Aplique la fórmula de deducción por flexión:

Consideraciones prácticas

Comprender la importancia de cada parámetro es vital para el éxito de las operaciones de plegado. El factor K, por ejemplo, influye en la cantidad de material que se necesita para el plegado, mientras que la tolerancia de plegado garantiza que el material se ajuste correctamente tras el plegado. Además, es esencial tener en cuenta la recuperación elástica, un fenómeno en el que el metal vuelve ligeramente a su forma original después del doblado, lo que puede hacer necesario doblar en exceso el material.

Siguiendo estos pasos y estudiando detenidamente cada parámetro, podrá calcular con precisión la tolerancia y la deducción de plegado necesarias para una fabricación precisa de chapa metálica.