¿Alguna vez se ha preguntado cómo calcular con precisión el margen de plegado para sus proyectos de fabricación de metal? En esta entrada del blog, exploraremos el fascinante mundo de las fórmulas y los cálculos del margen de plegado. Como ingeniero mecánico experimentado, le guiaré a través de los conceptos clave y le proporcionaré información práctica para ayudarle a dominar este aspecto crucial del diseño de chapa metálica. Prepárese para sumergirse y descubrir los secretos de la creación de pliegues precisos y eficaces en sus proyectos.
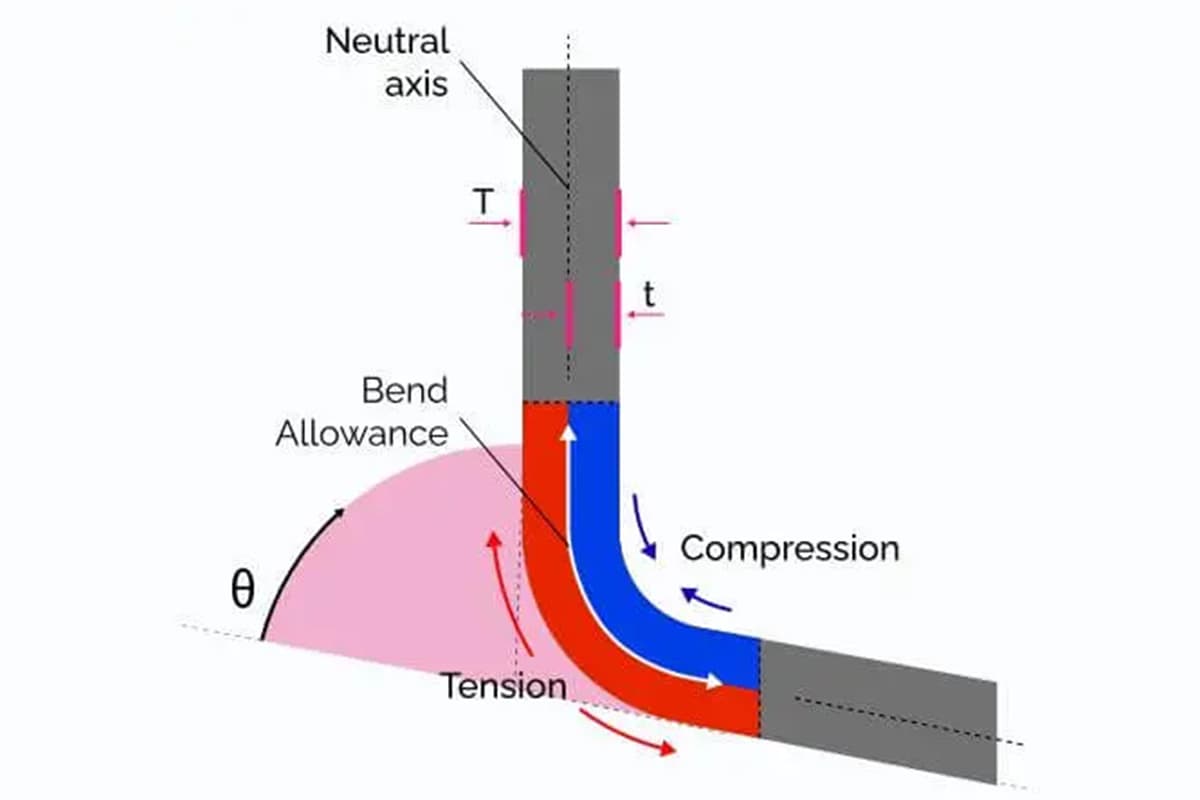
El margen de plegado es un concepto fundamental en el campo de la fabricación de chapa metálica, especialmente cuando se trabaja con operaciones de plegado. Se refiere a la longitud adicional de material necesaria para acomodar la curva en la chapa metálica. Comprender y calcular con precisión el margen de plegado es esencial para garantizar que las dimensiones finales de la pieza doblada cumplen las especificaciones de diseño.
El cálculo preciso de la tolerancia de plegado es vital en el proceso de fabricación. Cuando se dobla una chapa plana, el material de la parte exterior de la curva se estira, mientras que el material de la parte interior se comprime. Si no se tiene en cuenta esta deformación, el producto final no coincidiría con el diseño previsto, lo que provocaría imprecisiones y posibles fallos. La tolerancia de doblado ayuda a los fabricantes a ajustar las dimensiones del patrón plano, garantizando que la pieza doblada cumpla los requisitos precisos.
Varios parámetros críticos influyen en el cálculo de la tolerancia a la flexión:
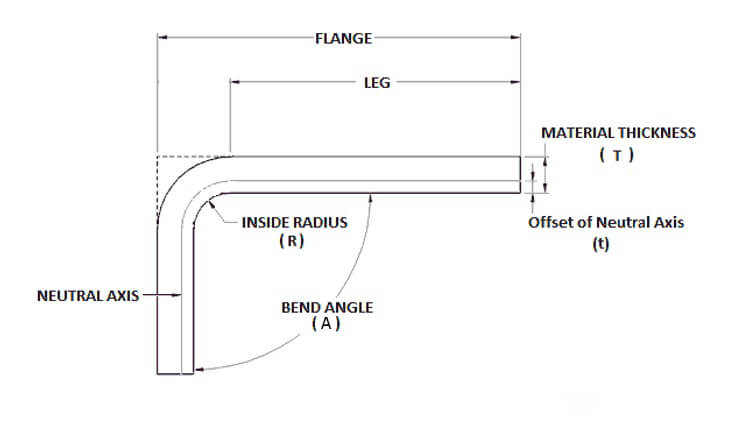
El concepto de margen de flexión es la siguiente: cuando se dobla una chapa, ésta tiene tres dimensiones: dos exteriores (L1 y L2) y una de espesor (T).
Es importante tener en cuenta que la suma de L1 y L2 es mayor que la longitud desplegada (L), y la diferencia entre ambas se conoce como sobremedida de flexión (K).
Por lo tanto, la longitud desplegada de una curva puede calcularse como L = L1 + L2 - K.
Lectura relacionada:
¿Cómo era la fórmula para margen de flexión creado? ¿Y cómo se calcula margen de flexión?
La tolerancia de curvatura depende del radio interior conformado. La abertura de la matriz en V inferior determina el radio interior (R.I.) de una pieza conformada. El radio interior para acero dulce es de 5/32 x abertura de matriz en V inferior (W) cuando el radio del punzón es inferior a 5/32 x W.
Si I.R.< Espesor del material (t)
Si I.R.> 2 x Espesor del material (t)
Donde A= (180 - Ángulo de curvatura incluido)
Si el radio interior es igual a t o 2t, o está comprendido entre t y 2t, la tolerancia de curvatura se calcula interpolando los valores de tolerancia de curvatura de las dos fórmulas mencionadas anteriormente.
Además, para calcular este subsidio de flexión, también puede utilizar la siguiente fórmula:
Esta fórmula tiene en cuenta las diversas geometrías y propiedades de las piezas a conformar.
El grosor del material (T), el ángulo de flexión (A), el interior radio de curvatura (R), y el factor K del material a curvar son los factores más críticos en este cálculo.
Como se desprende de la fórmula anterior, el cálculo de la sobremedida de flexión es un proceso sencillo.
Puede determinar el margen de flexión sustituyendo los valores mencionados en la fórmula.
Cuando el ángulo de flexión es de 90°, la fórmula de la tolerancia de flexión puede simplificarse como sigue:
Nota: El factor K para la mayoría de los materiales y espesores estándar suele situarse entre 0 y 0,5.
Puede calcular con precisión el valor del factor K utilizando lo siguiente Calculadora del factor K:
La fórmula de la sobremedida de curvado (BA) es esencial para calcular la longitud de material necesaria para formar una curva. Esta fórmula general es ampliamente aplicable a distintos materiales y métodos de doblado:
Dónde:
El factor K es crucial, ya que indica la posición del eje neutro, que no cambia de longitud durante la flexión. Normalmente, el factor K oscila entre 0,3 y 0,5 y varía en función del tipo de material, el grosor, el radio y el método de flexión.
Los distintos materiales tienen propiedades únicas que requieren ajustes en los cálculos de los márgenes de curvatura. Estos ajustes garantizan la precisión, especialmente en las curvas de 90°:
En el caso de materiales más blandos, como el latón o el cobre, la tolerancia de flexión se calcula de la siguiente manera:
BA = (0,55 × T) + (1,57 × R
Este ajuste tiene en cuenta la ductilidad del material y su menor resistencia a la deformación.
Para cobre o latón semiduro, acero blando y aluminio, la tolerancia de curvatura es:
BA = (0,64 x T) + (1,57 × R)
Estos materiales tienen una dureza moderada, por lo que requieren una tolerancia ligeramente superior a la de los materiales más blandos.
Para materiales más duros como el bronce, el cobre duro, el acero laminado en frío y el acero para muelles, la fórmula es:
BA = (0,71 x T) + (1,57 × R)
Estos materiales son más resistentes a la flexión, por lo que requieren una mayor sobremedida.
Para determinar la longitud plana total de la pieza de chapa metálica, se suma la sobremedida de plegado a las longitudes de las porciones planas:
Longitud plana = Longitud pierna 1 + BA + Longitud pierna 2
Este enfoque garantiza que las dimensiones finales de la pieza sean exactas después del plegado.
Consideremos una curvatura de 90° en una chapa de aluminio de 2 mm de espesor y un radio interior de curvatura de 5 mm. Utilizando la fórmula específica del material para cobre semiduro, latón, acero blando y aluminio:
BA = (0,64 × 2) + (1,57 × 5)
BA = 1,28 + 7,85=9,13
Si la pieza tiene dos secciones planas de 50 mm cada una, la longitud plana total sería:
Longitud plana = 50 + 9,13 + 50 = 109,13 mm
Además de la tolerancia de curvatura, la deducción de curvatura (BD) y el retranqueo exterior (OSSB) son importantes para realizar mediciones precisas:
Deducción por flexión (BD) = OSSB - BA
Dónde:
Estas formulaciones y consideraciones son esenciales para calcular con precisión los márgenes de plegado, garantizando que las piezas de chapa metálica se fabriquen con las dimensiones y el ajuste correctos.
El margen de plegado es un factor crítico en el proceso de plegado de chapa metálica, especialmente en materiales como el aluminio. Tiene en cuenta el estiramiento del material que se produce durante el plegado, garantizando unas dimensiones finales precisas. Aquí analizaremos la fórmula específica utilizada para las chapas de aluminio y su aplicación.
La tolerancia de flexión de una placa de aluminio puede calcularse mediante la siguiente fórmula:
𝐿=𝐿1+𝐿2-1,6𝑇
Dónde:
El valor 1,6𝑇 se deriva empíricamente, lo que significa que se ha establecido mediante experimentación práctica y experiencia de producción. Este factor tiene en cuenta el comportamiento del material durante la flexión, lo que garantiza la precisión de las dimensiones finales.
Es crucial señalar que esta fórmula es aplicable específicamente en determinadas condiciones:
Para determinar el tamaño expandido de la placa de aluminio, siga estos pasos:
Este cálculo le proporcionará la longitud de patrón plano necesaria antes del curvado, garantizando que la pieza curvada final tenga las dimensiones correctas.
La calculadora de sobremedida de plegado que se proporciona a continuación simplifica el proceso de cálculo del valor de la sobremedida de plegado, que es crucial para la fabricación precisa de chapas metálicas. La tolerancia de plegado es la longitud del eje neutro entre las líneas de plegado, que ayuda a determinar el tamaño correcto de la pieza en bruto para una pieza plegada.
El ángulo de curvatura, denominado θ, es un parámetro fundamental en la fórmula de la tolerancia de curvatura. Representa el ángulo por el que se dobla la chapa. El ángulo de curvatura suele medirse en grados, pero puede convertirse a radianes mediante la fórmula:
El radio interior, representado como r, es el radio de la curva interior de la curva. Este radio influye directamente en la cantidad de estiramiento y compresión que se produce dentro del material durante el doblado. Un radio interior más pequeño produce una deformación más significativa, que debe tenerse en cuenta en el cálculo de la tolerancia de flexión.
El grosor del material, denominado T, es el grosor de la chapa que se está doblando. Los materiales más gruesos experimentan un estiramiento y una compresión más pronunciados, lo que afecta a la tolerancia de plegado total. La medición exacta del espesor del material es esencial para calcular con precisión la tolerancia de plegado.
El factor K es un valor adimensional que representa la posición del eje neutro en relación con el espesor del material. El eje neutro es la línea teórica dentro del material que permanece inalterada en longitud durante la flexión. El factor K varía en función de las propiedades del material y de los métodos de flexión, oscilando normalmente entre 0,3 y 0,5 para la mayoría de los materiales. La fórmula para la posición del eje neutro es
Posición del eje neutro = K × T
El eje neutro es la línea imaginaria dentro del material que no cambia de longitud durante el plegado. Comprender su posición es crucial para calcular la sobremedida de flexión correcta.
La tolerancia de flexión, representada como BA, es la longitud del eje neutro necesaria para formar una curva. Se calcula mediante la fórmula:
Esta fórmula utiliza el ángulo de curvatura, el radio interior, el grosor del material y el factor K para garantizar un cálculo preciso de la tolerancia de curvatura.
La tabla de tolerancia de plegado es un recurso esencial para los profesionales que trabajan en la fabricación de chapa metálica. Proporciona una lista completa de parámetros clave como el grosor del material, el radio de curvatura, el ángulo de curvatura, la tolerancia de curvatura y los valores de deducción de curvatura para los materiales más comunes. Esta información es crucial para calcular con precisión la longitud de desarrollo de una pieza de chapa metálica después del plegado.
Más información:
| TV | Ángulo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Talla más corta |
| V4 | 90 | 0.9 | 1.4 | 2.8 | ||||||||||
| V4 | 120 | 0.7 | ||||||||||||
| V4 | 150 | 0.2 | ||||||||||||
| V6 | 90 | 1.5 | 1.7 | 2.15 | 4.5 | |||||||||
| V6 | 120 | 0.7 | 0.86 | 1 | ||||||||||
| V6 | 150 | 0.2 | 0.3 | 0.4 | ||||||||||
| V7 | 90 | 1.6 | 1.8 | 2.1 | 2.4 | 5 | ||||||||
| V7 | 120 | 0.8 | 0.9 | 1 | ||||||||||
| V7 | 150 | 0.3 | 0.3 | 0.3 | ||||||||||
| V8 | 90 | 1.6 | 1.9 | 2.2 | 2.5 | 5.5 | ||||||||
| V8 | 30 | 0.3 | 0.34 | 0.4 | 0.5 | |||||||||
| V8 | 45 | 0.6 | 0.7 | 0.8 | 1 | |||||||||
| V8 | 60 | 1 | 1.1 | 1.3 | 1.5 | |||||||||
| V8 | 120 | 0.8 | 0.9 | 1.1 | 1.3 | |||||||||
| V8 | 150 | 0.3 | 0.3 | 0.2 | 0.5 | |||||||||
| V10 | 90 | 2.7 | 3.2 | 7 | ||||||||||
| V10 | 120 | 1.3 | 1.6 | |||||||||||
| V10 | 150 | 0.5 | 0.5 | |||||||||||
| V12 | 90 | 2.8 | 3.65 | 4.5 | 8.5 | |||||||||
| V12 | 30 | 0.5 | 0.6 | 0.7 | ||||||||||
| V12 | 45 | 1 | 1.3 | 1.5 | ||||||||||
| V12 | 60 | 1.7 | 2 | 2.4 | ||||||||||
| V12 | 120 | 1.4 | 1.7 | 2 | ||||||||||
| V12 | 150 | 0.5 | 0.6 | 0.7 | ||||||||||
| V14 | 90 | 4.3 | 10 | |||||||||||
| V14 | 120 | 2.1 | ||||||||||||
| V14 | 150 | 0.7 | ||||||||||||
| V16 | 90 | 4.5 | 5 | 11 | ||||||||||
| V16 | 120 | 2.2 | ||||||||||||
| V16 | 150 | 0.8 | ||||||||||||
| V18 | 90 | 4.6 | 13 | |||||||||||
| V18 | 120 | 2.3 | ||||||||||||
| V18 | 150 | 0.8 | ||||||||||||
| V20 | 90 | 4.8 | 5.1 | 6.6 | 14 | |||||||||
| V20 | 120 | 2.3 | 3.3 | |||||||||||
| V20 | 150 | 0.8 | 1.1 | |||||||||||
| V25 | 90 | 5.7 | 6.4 | 7 | 17.5 | |||||||||
| V25 | 120 | 2.8 | 3.1 | 3.4 | ||||||||||
| V25 | 150 | 1 | 1 | 1.2 | ||||||||||
| V32 | 90 | 7.5 | 8.2 | 22 | ||||||||||
| V32 | 120 | 4 | ||||||||||||
| V32 | 150 | 1.4 | ||||||||||||
| V40 | 90 | 8.7 | 9.4 | 28 | ||||||||||
| V40 | 120 | 4.3 | 4.6 | |||||||||||
| V40 | 150 | 1.5 | 1.6 |
| TV | Ángulo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Talla más corta |
| V4 | 1.4 | 2.8 | ||||||||||||
| V6 | 1.6 | 4.5 | ||||||||||||
| V7 | 1.6 | 1.8 | 5 | |||||||||||
| V8 | 1.8 | 2.4 | 3.1 | 5.5 | ||||||||||
| V10 | 2.4 | 3.2 | 7 | |||||||||||
| V12 | 2.4 | 3.2 | 8.5 | |||||||||||
| V14 | 3.2 | 10 | ||||||||||||
| V16 | 3.2 | 4 | 4.8 | 11 | ||||||||||
| V18 | 4.8 | 13 | ||||||||||||
| V20 | 4.8 | 14 | ||||||||||||
| V25 | 4.8 | 5.4 | 6 | 17.5 | ||||||||||
| V32 | 6.3 | 6.9 | 22 |
| Ángulo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Talla más corta |
| 90 | 3.6 | 5.2 | 6.8 | 8.4 | 28 | ||||||||
| 120 | |||||||||||||
| 150 |
| MATERIAL | SPCC | SUS | Al （LY12） | SECC | ||||
|---|---|---|---|---|---|---|---|---|
| T | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK |
| T=0.6 | 1.25 | 1.26 | ||||||
| T=0.8 | 0.18 | 1.42 | 0.15 | 1.45 | 0.09 | 1.51 | ||
| T=1.0 | 0.25 | 1.75 | 0.20 | 1.80 | 0.30 | 1.70 | 0.38 | 1.62 |
| T=1.2 | 0.45 | 1.95 | 0.25 | 2.15 | 0.50 | 1.90 | 0.43 | 1.97 |
| T=1.4 | 0.64 | 2.16 | ||||||
| T=1.5 | 0.64 | 2.36 | 0.50 | 2.50 | 0.70 | 2.30 | ||
| T=1.6 | 0.69 | 2.51 | ||||||
| T=1.8 | 0.65 | 3.00 | ||||||
| T=1.9 | 0.60 | 3.20 | ||||||
| T=2.0 | 0.65 | 3.35 | 0.50 | 3.50 | 0.97 | 3.03 | 0.81 | 3.19 |
| T=2.5 | 0.80 | 4.20 | 0.85 | 4.15 | 1.38 | 3.62 | ||
| T=3.0 | 1.00 | 5.00 | 5.20 | 1.40 | 4.60 | |||
| T=3.2 | 1.29 | 5.11 | ||||||
| T=4.0 | 1.20 | 6.80 | 1.00 | 7.00 | ||||
| T=5.0 | 2.20 | 7.80 | 2.20 | 7.80 | ||||
| T=6.0 | 2.20 | 9.80 | ||||||
Nota:
Una tabla de tolerancia de plegado bien mantenida es una herramienta vital en la industria de fabricación de chapa metálica. Garantiza la precisión y eficacia del proceso de plegado y, en última instancia, permite obtener productos acabados más precisos y de mayor calidad. Al comprender y utilizar los valores de la tabla, los ingenieros y fabricantes pueden obtener resultados óptimos en sus proyectos.
En la fabricación de chapa metálica, lograr precisión y exactitud es crucial para crear piezas de alta calidad. Uno de los factores clave que desempeñan un papel importante en este proceso es el factor K. Comprender el factor K y su aplicación en el cálculo de la tolerancia de plegado es esencial para que los fabricantes produzcan piezas que cumplan las especificaciones exactas y funcionen de forma fiable en diversos sectores.
El factor K es un valor adimensional que representa la relación entre la distancia del eje neutro y el espesor del material. Es crucial para calcular con precisión la tolerancia de flexión, que determina la cantidad de material necesaria para lograr la flexión deseada. El eje neutro es una línea imaginaria dentro del material que no cambia de longitud durante el doblado. Al conocer el factor K, los fabricantes pueden predecir cómo se comportará el material al doblarse, lo que garantiza procesos de fabricación precisos y eficaces.
El factor K se calcula mediante la fórmula:
Dónde:
El uso del factor K en la fórmula de tolerancia de flexión ayuda a predecir el alargamiento y la compresión del material durante la flexión. La fórmula de la tolerancia de flexión es:
Para ilustrarlo, veamos un ejemplo sencillo. Supongamos que tenemos una pieza de chapa metálica con un grosor (T) de 2 mm, doblada en un ángulo de 90 grados (θ), con un radio interior (r) de 5 mm y un factor K (K) de 0,4.
1. Convierte el ángulo de curvatura a radianes:
2. Aplique los valores a la fórmula de la tolerancia de flexión:
Este cálculo muestra que se necesitan aproximadamente 9,11 mm de material a lo largo del eje neutro para lograr la curvatura deseada, lo que demuestra la importancia de un factor K preciso.
El factor K influye directamente en la precisión de los cálculos de la tolerancia de plegado. Un factor K preciso garantiza que las dimensiones finales de la pieza doblada coincidan con las especificaciones de diseño, lo que reduce el desperdicio de material y la necesidad de reprocesado. Esta precisión es vital para las industrias en las que las dimensiones exactas son cruciales para el ensamblaje y la funcionalidad de los componentes.
Los distintos materiales tienen propiedades mecánicas únicas, que dan lugar a valores de factor K variables. Los materiales más blandos, como el aluminio, suelen tener un factor K más bajo, mientras que los materiales más duros, como el acero inoxidable, tienen un factor K más alto. Comprender estas variaciones permite a los fabricantes seleccionar los valores de factor K adecuados para los distintos materiales, lo que garantiza la precisión de los cálculos y la eficacia de los procesos de fabricación.
A continuación encontrará respuestas a algunas preguntas frecuentes:
La fórmula de tolerancia de doblado se utiliza para calcular la longitud del eje neutro de un doblado en chapa metálica, que es crucial para determinar la longitud correcta del patrón plano antes de doblar el metal. Este cálculo garantiza que las dimensiones finales de la pieza doblada coincidan con las especificaciones del diseño.
La fórmula tiene en cuenta varios parámetros clave:
La fórmula general para la tolerancia a la flexión (BA) es:
Utilizando esta fórmula, puede calcular la longitud exacta de material necesaria para formar una curva, asegurándose de que el material no se estira excesivamente ni se comprime demasiado. Este margen de curvatura calculado se añade entonces a las longitudes de las patas de la pieza para desarrollar un patrón plano exacto, que es esencial para producir piezas con dimensiones precisas.
La fórmula de la sobremedida de plegado también está relacionada con la deducción de plegado, que es la longitud que hay que restar de la longitud total de la chapa para conseguir el patrón plano correcto. La deducción de plegado se calcula utilizando la sobremedida de plegado y el retranqueo exterior, lo que garantiza que las dimensiones finales de la pieza sean exactas después del plegado.
Por ejemplo, si va a doblar una chapa de acero inoxidable de 2 mm de grosor en un ángulo de 90° con un radio de curvatura interior de 3 mm y un factor K de 0,44, la tolerancia de curvatura puede calcularse del siguiente modo:
Este margen de plegado se utiliza para garantizar que el patrón plano se desarrolle correctamente, lo que da como resultado una pieza que cumple las especificaciones de diseño. En resumen, la fórmula de sobremedida de plegado es esencial para la fabricación precisa de chapa metálica, garantizando que las piezas finales se producen con las dimensiones correctas.
Para calcular la tolerancia de curvatura en chapa metálica, es necesario determinar varios parámetros clave: espesor del material (T), ángulo de curvatura (θ), radio interior (r) y factor K (K). La tolerancia de curvatura (BA) se calcula mediante la fórmula:
He aquí el proceso paso a paso:
Utilizando esta fórmula, para los mismos parámetros:
Siguiendo estos pasos y utilizando la fórmula adecuada, podrá calcular con precisión el margen de plegado de sus piezas de chapa metálica, garantizando una fabricación precisa.
El factor K es importante en la fórmula de la tolerancia a la flexión por varias razones, cada una de las cuales pone de relieve su importancia en la fabricación de chapa metálica de precisión. En primer lugar, representa la relación entre el eje neutro y el espesor del material. Durante el plegado, el eje neutro se desplaza desde su ubicación original a 50% del espesor del material hacia la superficie interior del pliegue. Este desplazamiento es crítico porque determina la cantidad de alargamiento que se produce en el material. El factor K ayuda a calcular esta nueva ubicación, que es esencial para realizar cálculos de flexión precisos.
En segundo lugar, el factor K es fundamental para calcular la sobremedida de doblado, que es la longitud de la fibra neutra desde el principio hasta el final del arco generado por el doblado. Este cálculo es necesario para determinar el tamaño plano de la chapa metálica necesario para conseguir la forma doblada deseada. El factor K influye directamente en la tolerancia de plegado, ya que tiene en cuenta el alargamiento del material durante el proceso de plegado.
Además, el uso del factor K permite realizar cálculos precisos de las deducciones de plegado, los retranqueos exteriores y la disposición plana general de la pieza. Esta precisión es vital porque garantiza que las dimensiones finales de la pieza doblada coincidan con las especificaciones de diseño, evitando los errores que podrían surgir al utilizar valores de factor K genéricos o inexactos.
El factor K varía en función de varios parámetros, como el tipo de material, el grosor, el método de conformado, el utillaje y el ángulo de plegado. Esta variabilidad significa que el factor K debe adaptarse a las condiciones específicas del proceso de plegado. Al tener en cuenta estos factores, el factor K ayuda a personalizar la fórmula de compensación del plegado para obtener resultados más precisos.
Por último, un valor correcto del factor K es esencial para evitar errores en las dimensiones finales de la chapa plegada. Los valores incorrectos del factor K pueden provocar imprecisiones en los márgenes de plegado, lo que da lugar a piezas que no cumplen las especificaciones requeridas. Por tanto, determinar y utilizar con precisión el factor K es fundamental para producir componentes de alta calidad.
En resumen, el factor K es importante porque permite calcular con precisión las tolerancias de plegado, tiene en cuenta el desplazamiento del eje neutro y considera los parámetros específicos del material y del proceso, todos ellos elementos esenciales para obtener resultados precisos y fiables en el plegado de chapa metálica.
La fórmula de la sobremedida de plegado en el plegado de chapa metálica suele incluir varias variables clave:
La tolerancia de flexión (BA) puede calcularse mediante la fórmula:
o
donde (0,017453) es (π/180) y (0,0078) es (π /180) x K) - factor.
Estas variables son esenciales para determinar con precisión la tolerancia de plegado, que es fundamental para la fabricación precisa de chapas metálicas.
Sí, la fórmula de la tolerancia de plegado puede variar significativamente en función del tipo de material, así como de otros factores como el grosor del material, el ángulo de plegado y el proceso de plegado específico.
El factor K, un componente crítico de la fórmula de tolerancia a la flexión, representa el desplazamiento del eje neutro teórico durante la flexión y varía en función del material. Por ejemplo, el acero dulce laminado en frío suele utilizar un factor K en torno a 0,446, mientras que otros materiales, como el acero inoxidable y el aluminio, tienen factores K diferentes debido a sus propiedades y comportamientos de flexión únicos.
La fórmula de la tolerancia de curvatura también incorpora el grosor del material y el ángulo de curvatura, que pueden variar de un material a otro. Una forma general de la fórmula es:
donde:
Los distintos materiales tienen propiedades diferentes, como la elasticidad, la resistencia a la tracción y la dirección del grano, que influyen en su comportamiento a la flexión. Por ejemplo, el aluminio se dobla más fácilmente que el acero, lo que requiere ajustes en el cálculo de la tolerancia de doblado. Además, doblar un metal a lo largo de su dirección de grano puede requerir más fuerza y una tolerancia de doblado diferente en comparación con el doblado a través del grano.
También hay que tener en cuenta la tendencia del material a recuperarse tras la flexión, lo que se conoce como recuperación elástica. Esto implica doblar ligeramente el material para tener en cuenta la recuperación elástica, influida por el tipo de material y sus propiedades.
En resumen, la fórmula de la tolerancia a la flexión debe adaptarse al material específico utilizado, teniendo en cuenta sus propiedades únicas, el grosor y el proceso de flexión implicado.
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
AR 
DE 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO