¿Se ha preguntado alguna vez cómo se transforma la chapa metálica en formas complejas? La deducción de pliegues, un concepto crucial en la fabricación de chapa metálica, tiene la clave. En esta entrada del blog, nos sumergiremos en los entresijos de la deducción de dobleces, explorando sus fórmulas, calculadoras y aplicaciones prácticas. Acompáñenos a desentrañar los secretos que se esconden tras la creación de componentes de chapa metálica precisos y bellos.
Calculadoras relacionadas:
La deducción de plegado es un concepto crucial en el campo de la fabricación de chapa metálica, especialmente en el proceso de plegado. Se conoce comúnmente como "cantidad de retroceso" y desempeña un papel importante en la determinación de las dimensiones exactas de una pieza doblada.
La deducción por plegado (BD) es la cantidad restada de la longitud total de la chapa plana para conseguir las dimensiones finales deseadas tras el plegado. Tiene en cuenta el material que se desplaza durante el proceso de plegado.
Importancia en el plegado de chapa
La deducción de doblado es esencial para calcular con precisión el patrón plano de una pieza de chapa metálica antes de doblarla. Garantiza que las dimensiones finales de la pieza doblada coincidan con las especificaciones del diseño. Si no se tiene en cuenta la deducción por plegado, la pieza puede acabar teniendo unas dimensiones incorrectas, lo que puede provocar problemas de montaje y funcionalidad.
Varios factores pueden influir en el valor de la deducción por doblez, entre ellos:
En la práctica, la deducción por flexión se determina mediante datos empíricos, directrices del fabricante o software especializado que tiene en cuenta las propiedades específicas del material y el proceso de flexión. Un cálculo preciso de la deducción por flexión es fundamental para garantizar que el producto final cumpla los requisitos de diseño y funcione correctamente en la aplicación prevista.
La deducción por plegado (BD) es un factor crítico en la fabricación de chapa metálica, que se utiliza para calcular la longitud plana de una pieza de chapa metálica. Tiene en cuenta el material que se desplaza durante el proceso de plegado. Este valor es esencial para garantizar que las dimensiones finales de la pieza doblada sean exactas.
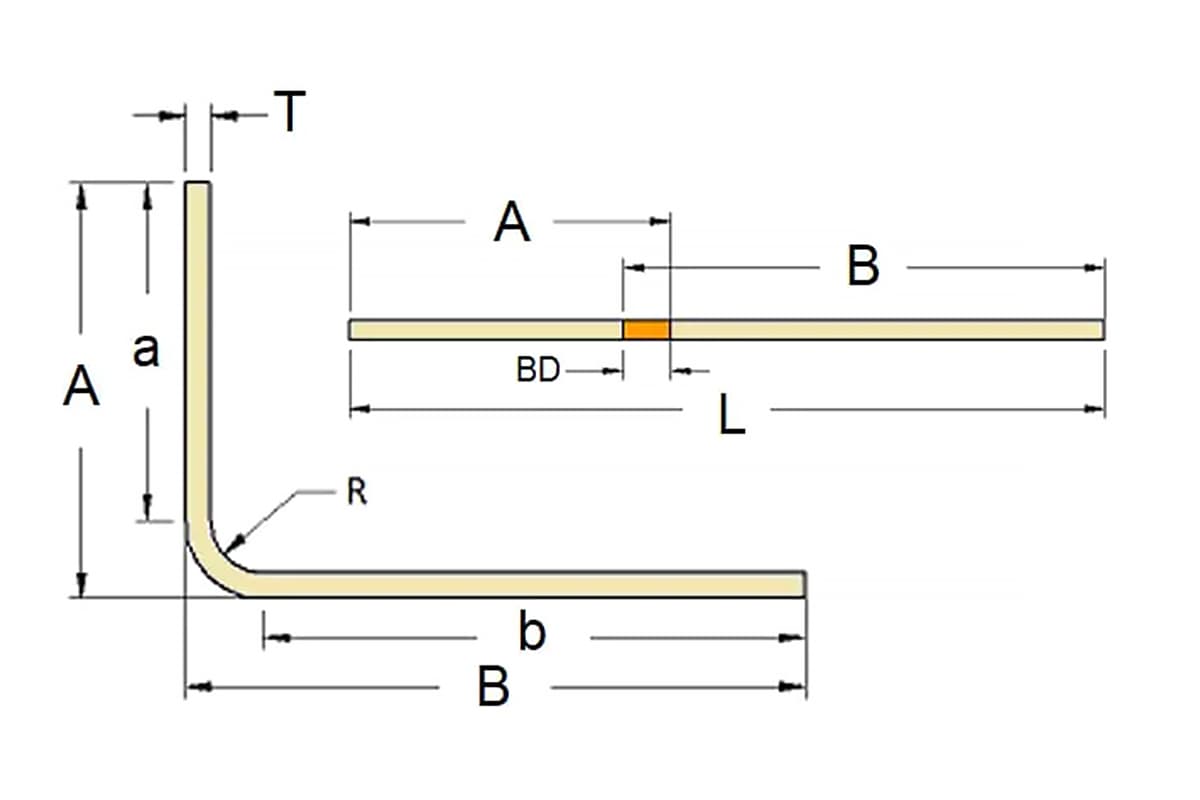
La fórmula de deducción de doblado se utiliza para determinar la longitud plana de una pieza de chapa antes de doblarla. La fórmula es la siguiente:
Lt=A+B-BD
Dónde:
La deducción de flexión en Solidworks sólo se utiliza para el cálculo de curvas de 90 grados en chapa metálica.
Sin embargo, también se puede utilizar para el cálculo del desdoblamiento de chapa sin 90 grados, pero es necesario utilizar el valor de la deducción por flexión para el desdoblamiento sin 90 grados de acuerdo con la tabla de coeficientes de flexión.
Cada fabricante tiene una tabla diferente, y puede haber errores. Es posible que algunas fábricas de chapa no utilicen a menudo curvados que no sean de 90 grados.
Hoy compartiré el método de cálculo para la deducción por flexión de 90 grados que conozco.
La deducción por plegado es un factor crucial en la fabricación de chapas metálicas, especialmente cuando se utilizan máquinas como prensas plegadoras. Representa la cantidad de material consumido durante el proceso de plegado. El cálculo exacto de las deducciones por plegado es esencial para obtener unas dimensiones precisas de la pieza y un uso eficaz del material. En este artículo se analizan tres métodos habituales para calcular las deducciones por plegado.
El método más sencillo utiliza un factor de multiplicación basado en el grosor del material:
Este método es rápido y sencillo, pero carece de precisión. Es adecuado para aplicaciones con menores requisitos de precisión o para estimaciones iniciales.
Un enfoque más refinado desarrollado por la industria de la chapa:
Deducción por flexión = 2 × espesor del material + 1/3 × espesor del material
Esta fórmula tiene en cuenta el alargamiento del material durante el plegado. Se deriva de: Longitud sin plegar = Longitud A + Longitud B - Deducción por flexión.
Cuando la deducción por flexión tiene en cuenta tanto el espesor del material como su alargamiento.
Una fórmula más sofisticada derivada de estudios empíricos:
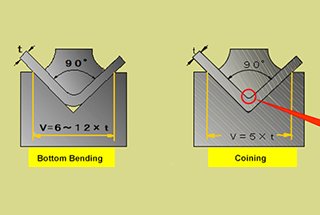
Deducción por flexión = 2 × t - (0,72t - 0,075V - 0,01)
Dónde:
Esta fórmula tiene en cuenta la influencia de la anchura inferior de la matriz en la deducción por flexión. Es especialmente precisa para chapas de acero al carbono, pero ha dado buenos resultados con otros materiales, como el aluminio, cuando la anchura de la matriz es unas 4 veces el grosor del material.
Consideraciones importantes
Conclusión
La elección del método de cálculo de la deducción por flexión adecuado depende de la precisión requerida, el tipo de material y la información disponible sobre el utillaje. Para trabajos de alta precisión, se recomienda la fórmula avanzada (Método 3), mientras que los métodos más sencillos pueden ser útiles para estimaciones rápidas o aplicaciones menos críticas.
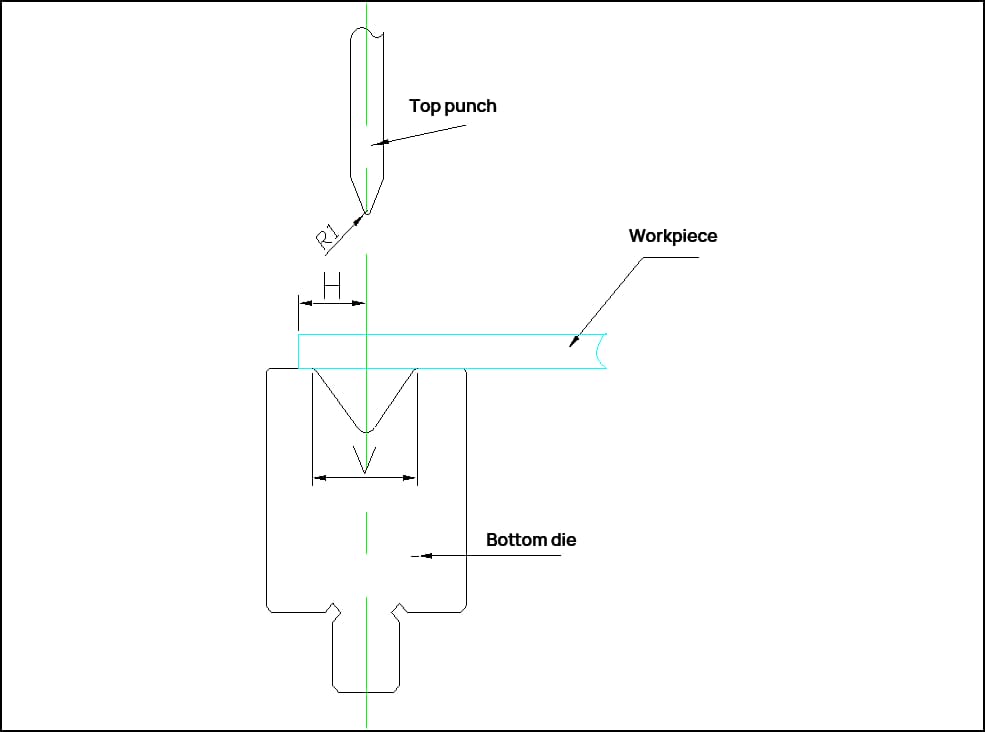
| V | Anchura del troquel w | Radio de curvatura | T | 30° | 45° | 60° | 90° | 120° | 150° | 180° | Capa exterior de doble curvatura de 90 | Tamaño mínimo de flexión H | Tamaño mínimo de la curva en Z (Z) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8.0 | 12.0 | R1 | 0.6 | 0.2 | 0.5 | 0.9 | 1.0 | 0.7 | 0.2 | 0.3 | 1.9 | 6.0 | 10.0 |
| 0.8 | 0.3 | 0.6 | 1.0 | 1.6 | 0.8 | 0.3 | 0.4 | 2.2 | |||||
| 1 | 0.3 | 0.7 | 1.1 | 1.7 | 0.9 | 0.3 | 0.5 | 2.5 | |||||
| 1.2 | 0.4 | 0.8 | 1.3 | 2.2 | 1.1 | 0.4 | 0.6 | 2.8 | |||||
| R2 | 0.6 | 0.2 | 0.5 | 0.9 | 1.6 | 0.7 | 0.2 | 0.3 | 1.9 | ||||
| 0.8 | 0.3 | 0.6 | 1.2 | 1.8 | 0.8 | 0.3 | 0.4 | 2.2 | |||||
| 1 | 0.3 | 0.7 | 1.2 | 2.0 | 0.9 | 0.3 | 0.5 | 2.5 | |||||
| 1.2 | 0.4 | 0.8 | 1.4 | 2.3 | 1.1 | 0.4 | 0.6 | 2.8 | |||||
| 10.0 | 14.0 | R1 | 1.5 | 0.7 | 1.2 | 1.6 | 2.5 | 1.3 | 0.5 | 0.7 | 3.2 | 7.0 | 11.0 |
| R2 | 1.5 | 0.6 | 1.0 | 1.5 | 2.7 | 1.3 | 0.5 | 0.7 | 3.5 | ||||
| 12.0 | 16.0 | R1 | 2 | 0.6 | 1.3 | 2.0 | 3.4 | 1.7 | 0.6 | 0.9 | 4.4 | 8.5 | 13.0 |
| R2 | 2 | 0.9 | 1.4 | 2.0 | 3.6 | 1.7 | 0.6 | 0.9 | 4.5 | ||||
| 16.0 | 26.0 | R1 | 2.5 | 0.7 | 1.5 | 2.4 | 4.3 | 2.2 | 0.8 | 1.1 | 5.6 | 12.0 | 20.0 |
| 3 | 0.8 | 1.7 | 2.8 | 5.1 | 2.8 | 0.8 | 1.3 | 5.8 | |||||
| R2 | 2.5 | 0.8 | 1.6 | 2.5 | 4.8 | 2.3 | 0.9 | 1.1 | 6.2 | ||||
| 3 | 1.0 | 2.0 | 3.0 | 5.2 | 2.8 | 1.0 | 1.3 | 6.4 | |||||
| 22.0 | 32.5 | R1 | 4 | 1.0 | 2.4 | 3.5 | 6.5 | 3.3 | 1.1 | 16.0 | 26.0 | ||
| R2 | 4 | 1.2 | 2.6 | 4.0 | 6.8 | 3.5 | 1.1 | ||||||
| 32.0 | 50.0 | R1 | 5 | 1.2 | 3.2 | 4.8 | 8.6 | 4.6 | 1.4 | 24.0 | 38.0 | ||
| 6 | 1.5 | 3.5 | 4.5 | 9.5 | 5.0 | 1.8 | |||||||
| R2 | 5 | 1.5 | 3.4 | 5.0 | 8.8 | 4.5 | 1.6 | ||||||
| 6 | 1.8 | 3.8 | 5.5 | 9.8 | 5.2 | 2.0 |
Explicación:
| Fórmula | 0.2t | 0.4t | 0.6t | 0.8t | 1.0t | 1.2t | 1.4t | 1.6t |
| Ángulo | 155-165° | 145-155° | 135-145° | 125-135° | 115-125° | 105-115° | 95-105° | 85-95° |
| Espesor (t) | 15-25° | 25-35° | 35-45° | 45-55° | 55-65° | 65-75° | 75-85° | |
| 0.5 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 |
| 0.6 | 0.12 | 0.24 | 0.36 | 0.48 | 0.60 | 0.72 | 0.84 | 0.96 |
| 0.8 | 0.16 | 0.32 | 0.48 | 0.64 | 0.80 | 0.96 | 1.12 | 1.28 |
| 1.0 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 |
| 1.2 | 0.24 | 0.48 | 0.72 | 0.96 | 1.20 | 1.44 | 1.68 | 1.92 |
| 1.5 | 0.30 | 0.60 | 0.90 | 1.20 | 1.50 | 1.80 | 2.10 | 2.40 |
| 2.0 | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 | 2.80 | 3.20 |
| 2.5 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 | 4.00 |
| 3.0 | 0.60 | 1.20 | 1.80 | 2.40 | 3.00 | 3.60 | 4.20 | 4.80 |
| 4.0 | 0.80 | 1.60 | 2.40 | 3.20 | 4.00 | 4.80 | 5.60 | 6.40 |
| 4.5 | 0.90 | 1.80 | 2.70 | 3.60 | 4.50 | 5.40 | 6.30 | 7.20 |
| 5.0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.00 | 8.00 |
| 6.0 | 1.20 | 2.40 | 3.60 | 4.80 | 6.00 | 7.20 | 8.40 | 9.60 |
| Fórmula | 0.3t | 0.5t | 0.7t | 0.9t | 1.1t | 1.3t | 1.5t | 1.7t |
| Ángulo | 155-165° | 145-155° | 135-145° | 125-135° | 115-125° | 105-115° | 95-105° | 85-95° |
| Espesor (t) | 15-25° | 25-35° | 35-45° | 45-55° | 55-65° | 65-75° | 75-85° | |
| 0.5 | 0.15 | 0.25 | 0.35 | 0.45 | 0.55 | 0.65 | 0.75 | 0.85 |
| 0.6 | 0.18 | 0.30 | 0.42 | 0.54 | 0.66 | 0.78 | 0.90 | 1.02 |
| 0.8 | 0.24 | 0.40 | 0.56 | 0.72 | 0.88 | 1.04 | 1.20 | 1.36 |
| 1.0 | 0.30 | 0.50 | 0.70 | 0.90 | 1.10 | 1.30 | 1.50 | 1.70 |
| 1.2 | 0.36 | 0.60 | 0.84 | 1.08 | 1.32 | 1.56 | 1.80 | 2.04 |
| 1.5 | 0.45 | 0.75 | 1.05 | 1.35 | 1.65 | 1.95 | 2.25 | 2.55 |
| 2.0 | 0.60 | 1.00 | 1.40 | 1.80 | 2.20 | 2.60 | 3.00 | 3.40 |
| 2.5 | 0.75 | 1.25 | 1.75 | 2.25 | 2.75 | 3.25 | 3.75 | 4.25 |
| 3.0 | 0.90 | 1.50 | 2.10 | 2.70 | 3.30 | 3.90 | 4.50 | 5.10 |
| 4.0 | 1.20 | 2.00 | 2.80 | 3.60 | 4.40 | 5.20 | 6.00 | 6.80 |
| 4.5 | 1.35 | 2.25 | 3.15 | 4.05 | 4.95 | 5.85 | 6.75 | 7.65 |
| 5.0 | 1.50 | 2.50 | 3.50 | 4.50 | 5.50 | 6.50 | 7.50 | 8.50 |
| 6.0 | 1.80 | 3.00 | 4.20 | 5.40 | 6.60 | 7.80 | 9.00 | 10.20 |
| No. | Ángulo /Grosor | 0.8 | 1.0 | 1.2 | 1.5 | 2.0 | 2.5 | 3.0 | 4.0 | 5.0 |
| 1 | 0 | 3.00 | 3.60 | 4.00 | 5.00 | 7.00 | 8.40 | 10.00 | 14.00 | 20.00 |
| 2 | 5 | 2.92 | 3.50 | 3.89 | 4.86 | 6.81 | 8.17 | 9.72 | 13.61 | 19.44 |
| 3 | 10 | 2.83 | 3.40 | 3.78 | 4.72 | 6.61 | 7.93 | 9.44 | 13.22 | 18.89 |
| 4 | 15 | 2.75 | 3.30 | 3.67 | 4.58 | 6.42 | 7.70 | 9.17 | 12.83 | 18.33 |
| 5 | 20 | 2.67 | 3.20 | 3.56 | 4.44 | 6.22 | 7.47 | 8.89 | 12.44 | 17.78 |
| 6 | 25 | 2.58 | 3.10 | 3.44 | 4.31 | 6.03 | 7.23 | 8.61 | 12.06 | 17.22 |
| 7 | 30 | 2.50 | 3.00 | 3.33 | 4.17 | 5.83 | 7.00 | 8.33 | 11.67 | 16.67 |
| 8 | 35 | 2.42 | 2.90 | 3.22 | 4.03 | 5.64 | 6.77 | 8.06 | 11.28 | 16.11 |
| 9 | 40 | 2.33 | 2.80 | 3.11 | 3.89 | 5.44 | 6.53 | 7.78 | 10.89 | 15.56 |
| 10 | 45 | 2.25 | 2.70 | 3.00 | 3.75 | 5.25 | 6.30 | 7.50 | 10.50 | 15.00 |
| 11 | 50 | 2.17 | 2.60 | 2.89 | 3.61 | 5.06 | 6.07 | 7.22 | 10.11 | 14.44 |
| 12 | 55 | 2.08 | 2.50 | 2.78 | 3.47 | 4.86 | 5.83 | 6.94 | 9.72 | 13.89 |
| 13 | 60 | 2.00 | 2.40 | 2.67 | 3.33 | 4.67 | 5.60 | 6.67 | 9.33 | 13.33 |
| 14 | 65 | 1.92 | 2.30 | 2.56 | 3.19 | 4.47 | 5.37 | 6.39 | 8.94 | 12.78 |
| 15 | 70 | 1.83 | 2.20 | 2.44 | 3.06 | 4.28 | 5.13 | 6.11 | 8.56 | 12.22 |
| 16 | 75 | 1.75 | 2.10 | 2.33 | 2.92 | 4.08 | 4.90 | 5.83 | 8.17 | 11.67 |
| 17 | 80 | 1.67 | 2.00 | 2.22 | 2.78 | 3.89 | 4.67 | 5.56 | 7.78 | 11.11 |
| 18 | 85 | 1.58 | 1.90 | 2.11 | 2.64 | 3.69 | 4.43 | 5.28 | 7.39 | 10.56 |
| 19 | 90 | 1.50 | 1.80 | 2.00 | 2.50 | 3.50 | 4.20 | 5.00 | 7.00 | 10.00 |
| 20 | 95 | 1.42 | 1.70 | 1.89 | 2.36 | 3.31 | 3.97 | 4.72 | 6.61 | 9.44 |
| 21 | 100 | 1.33 | 1.60 | 1.78 | 2.22 | 3.11 | 3.73 | 4.44 | 6.22 | 8.89 |
| 22 | 105 | 1.25 | 1.50 | 1.67 | 2.08 | 2.92 | 3.50 | 4.17 | 5.83 | 8.33 |
| 23 | 110 | 1.17 | 1.40 | 1.56 | 1.94 | 2.72 | 3.27 | 3.89 | 5.44 | 7.78 |
| 24 | 115 | 1.08 | 1.30 | 1.44 | 1.81 | 2.53 | 3.03 | 3.61 | 5.06 | 7.22 |
| 25 | 120 | 1.00 | 1.20 | 1.33 | 1.67 | 2.33 | 2.80 | 3.33 | 4.67 | 6.67 |
| 26 | 125 | 0.92 | 1.10 | 1.22 | 1.53 | 2.14 | 2.57 | 3.06 | 4.28 | 6.11 |
| 27 | 130 | 0.83 | 1.00 | 1.11 | 1.39 | 1.94 | 2.33 | 2.78 | 3.89 | 5.56 |
| 28 | 135 | 0.75 | 0.90 | 1.00 | 1.25 | 1.75 | 2.10 | 2.50 | 3.50 | 5.00 |
| 29 | 140 | 0.67 | 0.80 | 0.89 | 1.11 | 1.56 | 1.87 | 2.22 | 3.11 | 4.44 |
| 30 | 145 | 0.58 | 0.70 | 0.78 | 0.97 | 1.36 | 1.63 | 1.94 | 2.72 | 3.89 |
| 31 | 150 | 0.50 | 0.60 | 0.67 | 0.83 | 1.17 | 1.40 | 1.67 | 2.33 | 3.33 |
| 32 | 155 | 0.42 | 0.50 | 0.56 | 0.69 | 0.97 | 1.17 | 1.39 | 1.94 | 2.78 |
| 33 | 160 | 0.33 | 0.40 | 0.44 | 0.56 | 0.78 | 0.93 | 1.11 | 1.56 | 2.22 |
| 34 | 165 | 0.25 | 0.30 | 0.33 | 0.42 | 0.58 | 0.70 | 0.83 | 1.17 | 1.67 |
| 35 | 170 | 0.17 | 0.20 | 0.22 | 0.28 | 0.39 | 0.47 | 0.56 | 0.78 | 1.11 |
| 36 | 175 | 0.08 | 0.10 | 0.11 | 0.14 | 0.19 | 0.23 | 0.28 | 0.39 | 0.56 |
| 37 | 180 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
1) La tabla de deducción de plegado es aplicable a los procesos de plegado de chapas metálicas en los que no se utiliza placa de prensado y la anchura de la chapa es superior a tres veces el espesor (t).
2) Al curvar en la máquina curvadora, los cálculos pueden realizarse según esta tabla.
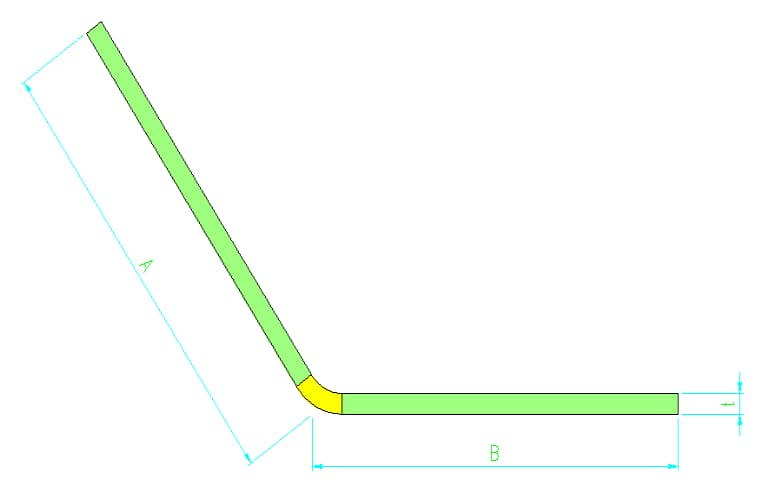
3) Según las dimensiones indicadas en el diagrama, la fórmula de cálculo para el tamaño desplegado de la pieza doblada es la siguiente:
L=a+b-y
Dónde:
4) Debido a los numerosos factores que influyen en el plegado de chapa metálica, esta tabla de valores de deducción por plegado de chapa metálica se proporciona únicamente como referencia.
La precisión dimensional de las piezas dobladas está relacionada con la precisión posicional del tope trasero de la plegadora y la precisión de la chapa. máquina de corte de metal. La utilización de máquinas fiables para los procesos de corte y plegado puede resolver estos problemas.
Un factor crítico que afecta a la precisión dimensional de las piezas de trabajo dobladas es la precisión del desarrollo de la chapa plana. Cuando una chapa plana se dobla en una pieza de trabajo con un ángulo específico, la medición de las dimensiones de la pieza doblada revela que no son iguales a las dimensiones de la chapa plana, como se muestra en la ilustración.
Esta discrepancia se conoce como deducción por flexión.
Si la deducción de plegado es imprecisa, el tamaño del patrón plano será impreciso e, independientemente de la precisión de las operaciones posteriores, la pieza final no cumplirá la precisión dimensional requerida.
La deducción por flexión es compleja, y un método rudimentario consiste simplemente en utilizar el doble del grosor del material.
Sin embargo, este enfoque es bastante rudimentario. Un método más refinado consiste en aplicar la teoría del eje neutro de la norma DIN 6935, que implica calcular un factor "k" y combinarlo con el grosor y el ángulo de la chapa que se va a doblar.
Con esta fórmula se obtiene una deducción por flexión más precisa. Sin embargo, incluso las deducciones por flexión calculadas según la teoría del eje neutro de la norma DIN 6935 pueden no ser lo suficientemente precisas, ya que las deducciones reales también dependen de las características del material, el espesor, el ángulo de flexióny el utillaje utilizado.
Los diferentes materiales, espesores y métodos de cálculo dan lugar a deducciones de flexión variables, como se muestra en la tabla siguiente.
Tabla Valor de deducción para cotas de flexión correspondientes a diferentes materiales, espesores y métodos
| Espesor de la placa S/mm | Muere | Material | -S × 2 | DIN6935 | Base de datos |
| 1.5 | V12/78 | DC04 | -3.00 | -3.00 | -2.90 |
| 1.5 | V08/78 | DC04 | -3.00 | -2.80 | -2.70 |
| 1.5 | V1278 | X5CrNi1810 | -3.00 | -3.00 | -3.10 |
| 4 | V24/78 | S235JRG2 | -8.00 | -7.60 | -7.09 |
| 4 | V30/78 | S235JRG2 | -8.00 | -7.57 | -7.26 |
| 4 | V24/78 | X5CrNi1810 | -8.00 | -8.01 | -7.57 |
| 4 | V30/78 | X5CrNi1810 | -8.00 | -7.90 | -8.01 |
| 6 | V30/78 | S235JRG2 | -12.00 | -11.20 | -10.35 |
| 6 | V4078 | S235JRG2 | -12.00 | -11.60 | -10.62 |
| 6 | V30/78 | X5CrNi1810 | -12.00 | -11.20 | -10.89 |
| 6 | V4078 | X5CrNi1810 | -12.00 | -11.60 | -11.60 |
Por ejemplo, para una chapa S235JRG2 de 4 mm de espesor utilizando una matriz inferior V30, la deducción por flexión varía según el método: el doble del espesor del material da como resultado 8 mm, la fórmula DIN 6935 da 7,57 mm y el valor empírico de la base de datos da 7,26 mm.
Existen discrepancias entre los métodos, que se hacen aún más significativas cuando las piezas de trabajo requieren múltiples dobleces, lo que da lugar a desviaciones acumuladas mayores. Los valores empíricos de la base de datos se derivan de extensas pruebas prácticas y se almacenan en la base de datos, lo que proporciona la máxima precisión.
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
AR 
DE 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO