¿Cómo garantizan los ingenieros la resistencia y durabilidad de las vigas bajo distintas cargas? Este artículo profundiza en los principios del esfuerzo cortante de flexión y las condiciones necesarias para mantener la resistencia de las vigas. Abarca la distribución de tensiones en diferentes secciones de vigas (rectangulares, circulares, en forma de I y anulares de pared delgada) y sugiere formas de mejorar el rendimiento de las vigas mediante un mejor diseño y un mejor uso de los materiales. Aprenda cómo interactúan las tensiones de cizalladura y flexión, y descubra consejos prácticos para optimizar la construcción y aplicación de vigas.
En la sección transversal de una viga sometida a una fuerza transversal se produce un momento flector y una fuerza cortante, lo que da lugar a una tensión normal y a una tensión cortante en la sección transversal. A continuación se analizará el esfuerzo cortante de flexión de varias secciones comunes de vigas.
Se corta un pequeño segmento de longitud dx de la viga sometida a flexión por fuerzas transversales. La viga no tiene carga y los esfuerzos cortantes a ambos lados del segmento son iguales pero en sentidos opuestos. El momento flector en la sección derecha es mayor que en la sección izquierda, lo que da lugar a tensiones normales diferentes en las dos secciones.
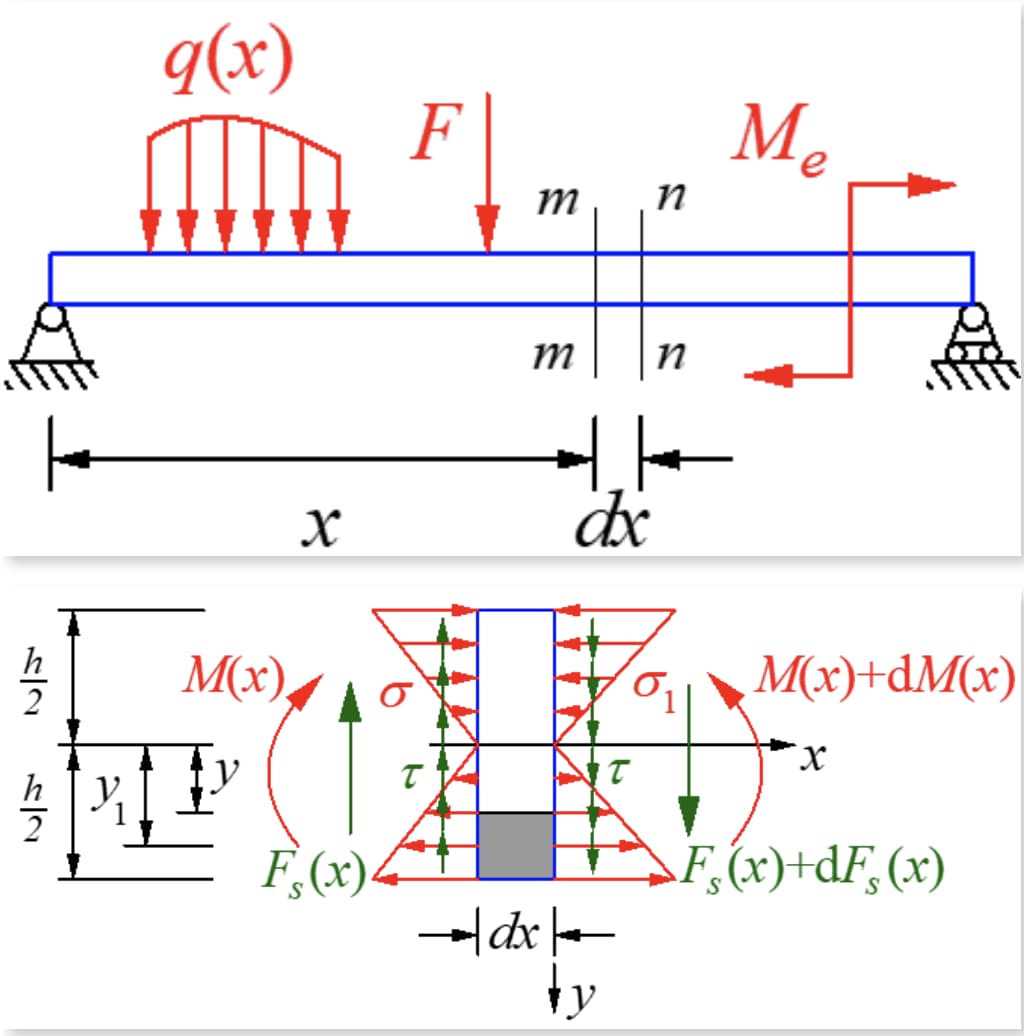
Para una sección rectangular estrecha, el esfuerzo cortante es tangente al límite en ambos lados de la viga debido a la ausencia de esfuerzo cortante en el lateral. Esto significa que, como la viga está doblada simétricamente y paralela al límite, el esfuerzo cortante en el eje y del eje de simetría debe estar en la dirección y y cambia poco a lo largo de la dirección del ancho.
Por lo tanto, se hacen las siguientes suposiciones sobre la ley de distribución del esfuerzo cortante en la sección transversal:
Cuando la relación altura-anchura de la sección es superior a 2, la solución basada en la hipótesis anterior es suficientemente precisa en comparación con la solución exacta de la teoría elástica.
Según el teorema de reciprocidad del esfuerzo cortante, debe haber un esfuerzo cortante igual al tamaño de la sección transversal en la sección longitudinal perpendicular a la sección transversal. Corte un micro segmento a lo largo del plano longitudinal con el eje neutro de momento alejado de y, y tome el micro elemento en el lado inferior del plano longitudinal. Las fuerzas son las que se muestran en la figura siguiente.
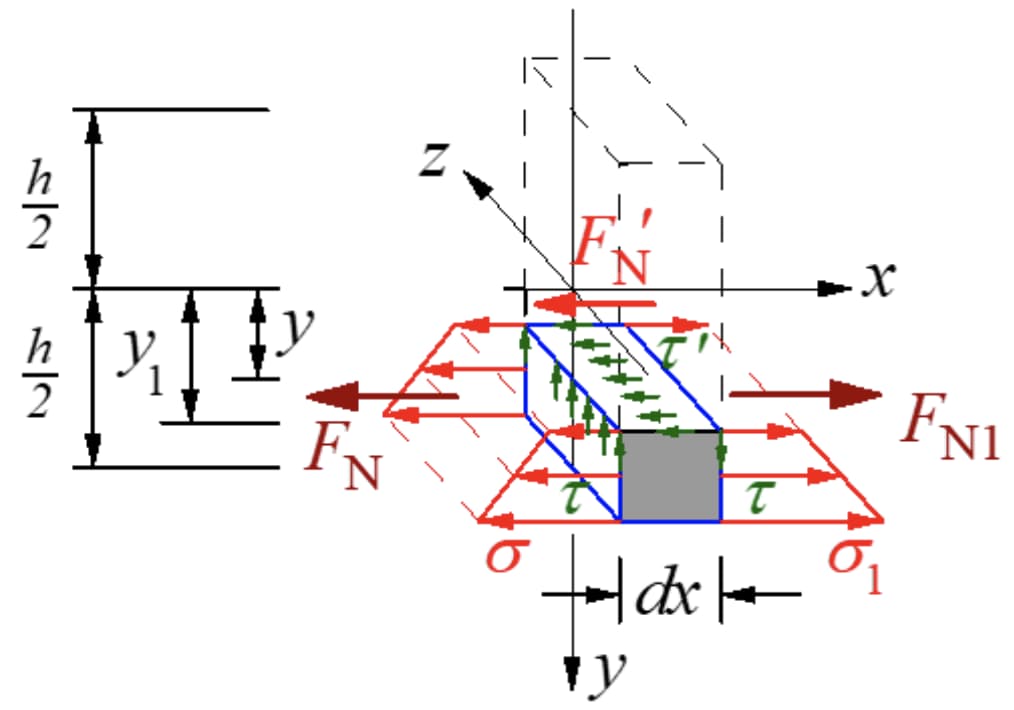
La fuerza resultante de la tensión normal en la sección izquierda es:
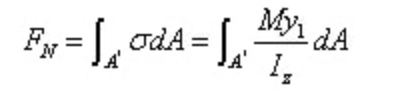
La fuerza resultante de la tensión normal en la sección derecha es：
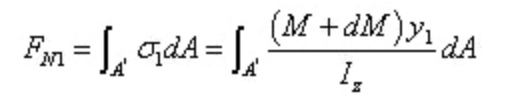
Es evidente que las dos resultantes son de tamaños diferentes. Debe existir una fuerza a lo largo de la dirección axial en la sección longitudinal para mantener el equilibrio del microsegmento. Esta fuerza es el resultado de la tensión de cizallamiento, lo que confirma la presencia de tensión de cizallamiento en la sección longitudinal.
Dado que dx es una cantidad pequeña, que el esfuerzo cortante en el plano longitudinal se distribuya uniformemente：.
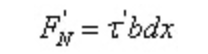
Según las condiciones de equilibrio：
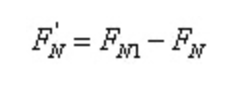
Eso es,
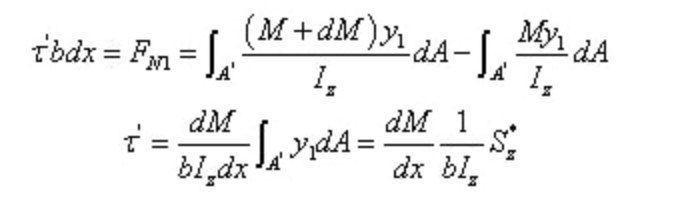
Entre,
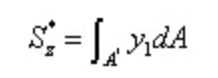
A partir del teorema recíproco del esfuerzo cortante y de la relación diferencial entre el esfuerzo cortante y el momento flector:
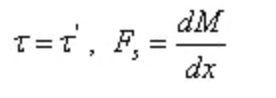
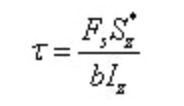
De los cuales:
Entre,
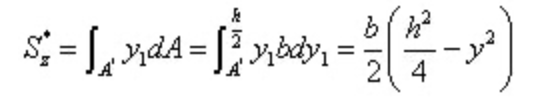
Sustituir en la fórmula de cálculo del esfuerzo cortante
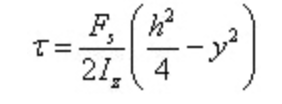
El esfuerzo cortante se distribuye en parábola a lo largo de la altura de la sección.
Cuando y=0, se produce el esfuerzo cortante máximo en la sección en el eje neutro
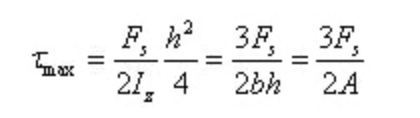
La deformación angular es
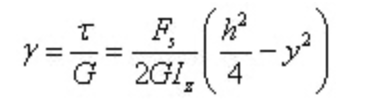
Se puede observar que la deformación angular también se distribuye en forma de parábola a lo largo de la altura de la sección.
En este momento, la forma de alabeo de la sección transversal cuando se dobla la fuerza transversal se muestra en la figura siguiente, lo que verifica que la deformación por flexión de la fuerza transversal no cumple la suposición de plano.
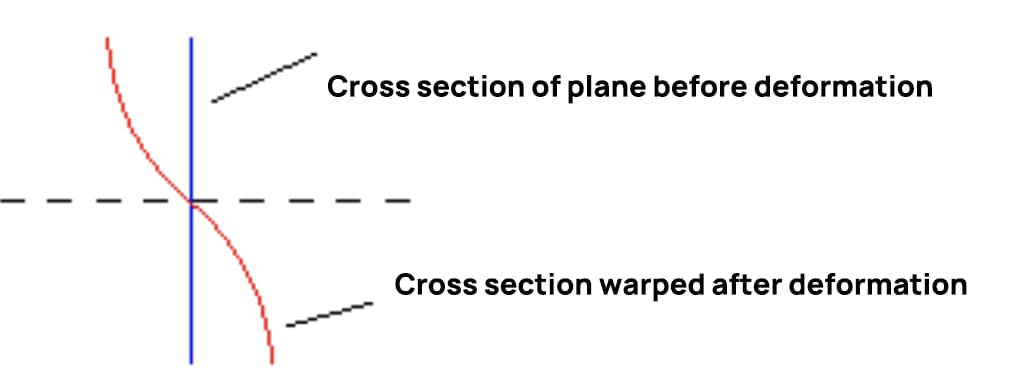
Cuando la fuerza de cizallamiento permanece constante, la tensión de cizallamiento en secciones transversales consecutivas es igual, y el grado de alabeo también es igual. La longitud de las fibras longitudinales no cambia debido al alabeo de la sección, por lo que no se producirá tensión normal adicional. Si el esfuerzo cortante cambia con la posición de la sección, el grado de alabeo en dos secciones consecutivas será diferente, lo que provocará una tensión normal adicional en la sección.
Para secciones simétricas de otras formas, la solución aproximada del esfuerzo cortante puede derivarse utilizando el método anterior.
Para una sección rectangular, en la fórmula de cálculo de tensiones, la anchura de la sección (b) es constante, y el momento estático de la mitad de la sección transversal a un lado del eje neutro con respecto al eje neutro es el mayor. En consecuencia, el esfuerzo cortante en cada punto del eje neutro es el mayor.
Para las secciones simétricas de otras formas, el esfuerzo cortante máximo en la sección transversal se localiza normalmente en varios puntos del eje neutro, con la excepción de las secciones con una anchura significativamente mayor en el eje neutro (como las secciones transversales) o algunas secciones con anchura variable (como las secciones en triángulo isósceles).
Por lo tanto, para las vigas de sección en I, anular y circular, a continuación se tratará principalmente el esfuerzo cortante máximo en cada punto del eje neutro.
El esfuerzo cortante en cada punto del borde de una sección circular es tangente a la circunferencia, según el teorema recíproco del esfuerzo cortante. En cada punto del eje de simetría, el esfuerzo cortante debe estar en la dirección y. Puede suponerse que la distribución del esfuerzo cortante converge en un punto del eje de simetría para cada punto a lo largo de la anchura y desde el eje neutro, y las componentes del esfuerzo cortante a lo largo de la dirección y en cada punto a lo largo de la anchura son iguales.
El esfuerzo cortante máximo de la sección circular sigue estando en el eje neutro, y su dirección es paralela a la fuerza externa, con el mismo valor en cada punto del eje neutro.
El esfuerzo cortante máximo es
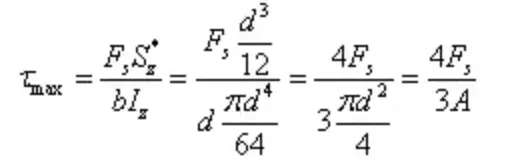
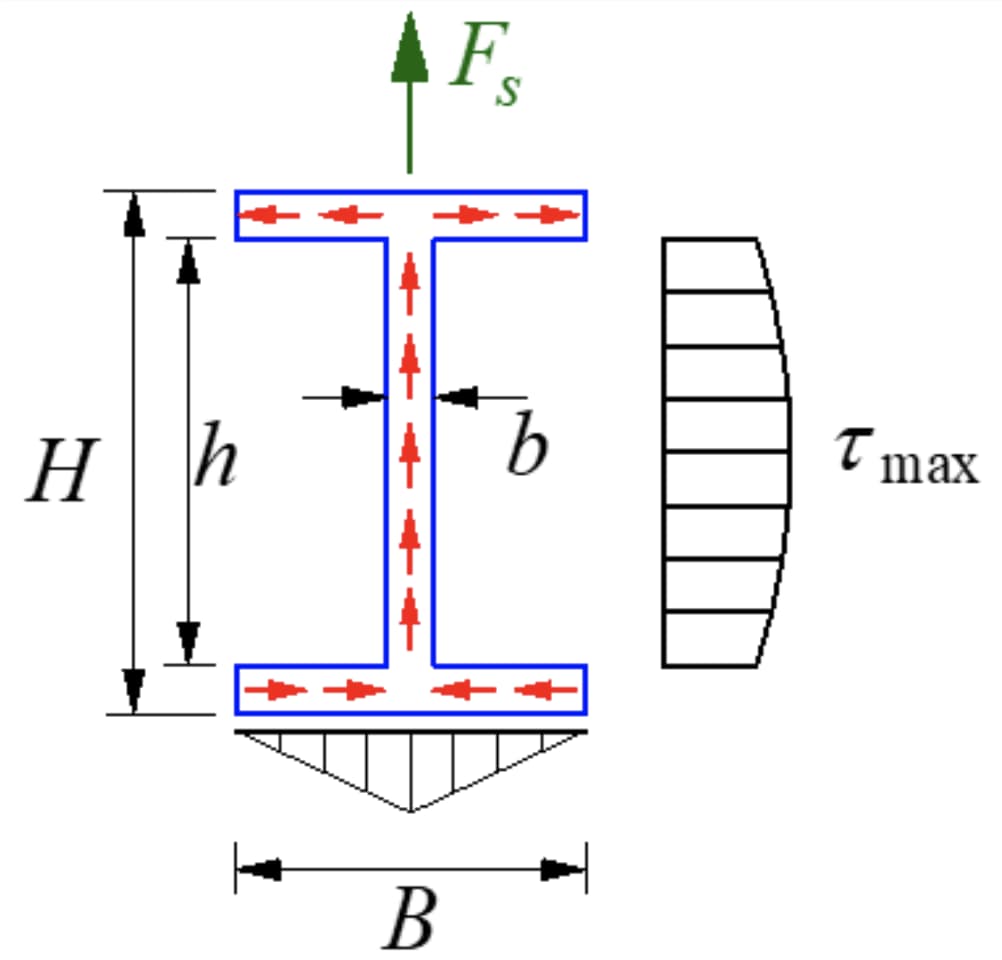
La sección en forma de I es una sección abierta de pared delgada con una distribución de tensiones como la que se muestra en la figura. La magnitud del esfuerzo cortante a lo largo del espesor de la pared es igual, lo que se conoce como flujo de esfuerzo cortante, que fluye en la dirección del cizallamiento.
La componente del esfuerzo cortante paralela al eje y en el ala es secundaria y despreciable, centrándose principalmente en la componente paralela al lado largo del ala. El esfuerzo cortante en el alma tiene una distribución parabólica, cuyo tamaño se muestra en la figura.
El esfuerzo cortante máximo se produce en el eje neutro.
En caso de Acero en forma de Iel esfuerzo cortante máximo:
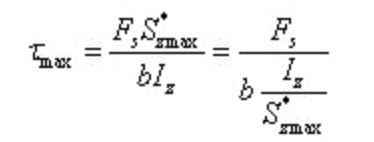
Donde, b es el espesor de la banda, e Iz/s*zmax puede obtenerse consultando la tabla de perfiles de acero.
Si se trata de una sección en forma de I compuesta por tres rectángulos largos y estrechos, los esfuerzos cortantes máximos y mínimos en el alma pueden obtenerse de la siguiente manera:
De las dos fórmulas anteriores se deduce que la anchura del alma es mucho menor que la anchura del ala, por lo que el esfuerzo cortante máximo en el alma no difiere mucho del esfuerzo cortante mínimo.
Por lo tanto, se puede considerar que el esfuerzo cortante en el alma está distribuido de forma aproximadamente uniforme.
El esfuerzo cortante resultante en el alma representa 95-97% del esfuerzo cortante total, y el esfuerzo cortante en la sección transversal es soportado en su mayor parte por el alma.
Dado que el alma soporta casi toda la fuerza de cizallamiento de la sección y que la tensión de cizallamiento en el alma se distribuye casi uniformemente, la tensión de cizallamiento máxima puede calcularse aproximadamente dividiendo la fuerza de cizallamiento por el área de la sección transversal del asta ventral:
Al mismo tiempo, toda la zona de Viga en I El ala está más alejada del eje neutro y la tensión normal en cada punto es relativamente grande, por lo que el ala soporta la mayor parte del momento flector de la sección.
El espesor de la sección anular de pared delgada es d, el radio medio del anillo es r, y el espesor es muy inferior al radio medio, por lo que cabe suponer que:
El esfuerzo cortante en la sección transversal es igual a lo largo del espesor de la pared;
La dirección del esfuerzo cortante es tangente a la línea central de la sección, y la dirección del flujo del esfuerzo cortante es a lo largo de la dirección del esfuerzo cortante.
El esfuerzo cortante máximo se localiza en el eje neutro:
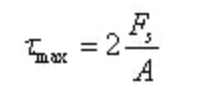
Donde, A es el área de la sección anular.
Condición de resistencia a la tensión normal de flexión:
En las secciones axisimétricas neutras, la tensión normal máxima de tracción y la tensión normal máxima de compresión son iguales.
Se suelen utilizar materiales plásticos y sus condiciones de resistencia:
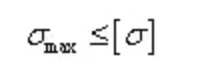
En cuanto a la sección con eje neutro asimétrico, la tensión normal máxima de tracción y la tensión normal máxima de compresión no son iguales.
Se suelen utilizar materiales frágiles y sus condiciones de resistencia:
La condición de resistencia del esfuerzo cortante de flexión es:
La tensión normal de flexión es el principal factor que controla la viga.
Por lo tanto, la condición de resistencia de la tensión normal de flexión suele ser la base principal para el diseño de vigas.
A partir de la condición de resistencia, para mejorar la capacidad portante de la viga, deben considerarse dos aspectos:
Por un lado, el esfuerzo de la viga debe disponerse razonablemente para reducir el momento flector máximo;
Por otro lado, se adopta una forma de sección razonable para mejorar el coeficiente de sección de flexión de la sección y aprovechar al máximo las propiedades del material.
Mejorar el estado tensional de la viga e intentar reducir el momento flector máximo en la viga.
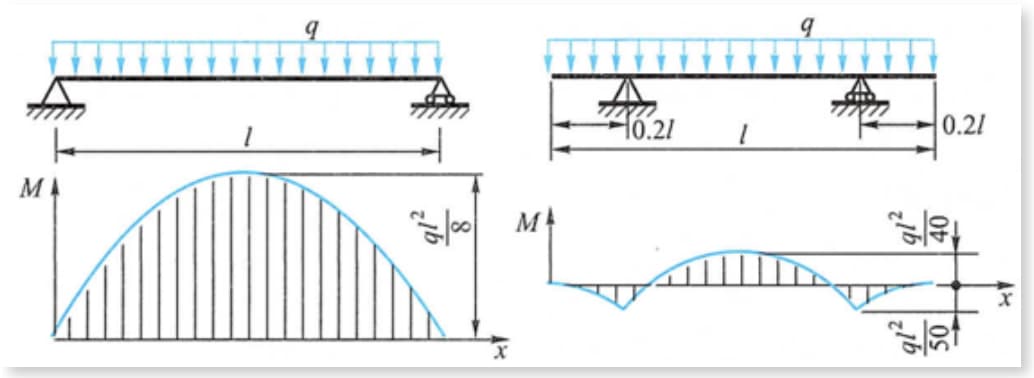
Como se muestra en la fig., el momento flector máximo en la viga bajo carga uniforme se reduce considerablemente cuando el apoyo se desplaza hacia el interior una cierta distancia desde las posiciones de ambos extremos de la viga.
Por ejemplo, la viga y el contenedor cilíndrico de la grúa de pórtico, cuyo punto de apoyo se desplaza ligeramente hacia el centro, pueden conseguir el efecto de reducir el momento de flexión máximo.
Cuanto mayor sea el coeficiente de sección a flexión, menor será la tensión y mayor la capacidad portante de la viga.
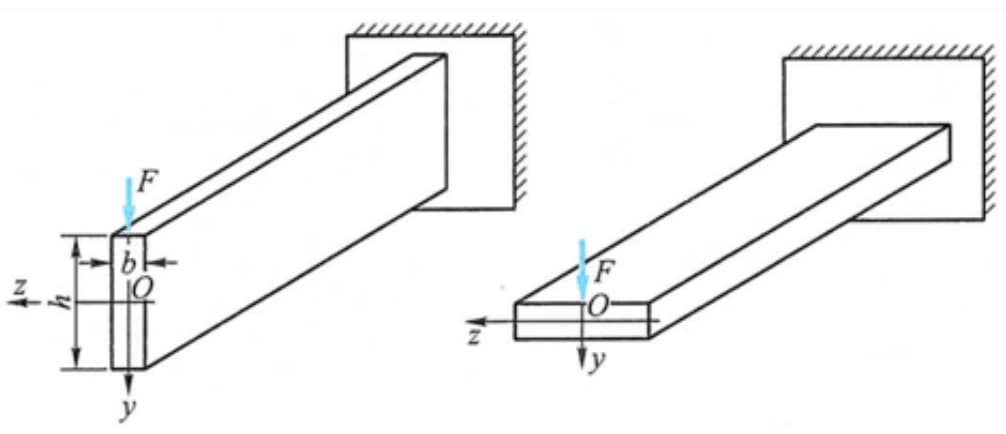
Por ejemplo, cuando la viga se carga en dirección vertical, el coeficiente de flexión de la sección es mayor cuando la sección se coloca verticalmente, por lo que es más razonable colocarla verticalmente que horizontalmente.
Al tiempo que mejoramos el coeficiente de sección de flexión de la sección, también esperamos utilizar menos materiales para lograr una mayor economía.
Por lo tanto, la relación entre el coeficiente de sección de flexión y el área de la sección se utiliza generalmente para medir la racionalidad del diseño de la sección.
Con la misma sección transversal, la sección rectangular (altura mayor que anchura) es más razonable que la circular, mientras que la sección en forma de I o de caja es más razonable que la rectangular.
Por lo tanto, para aprovechar al máximo los materiales, éstos deben colocarse lo más lejos posible del eje neutro.
Al debatir la forma razonable de la sección, el propiedades mecánicas del material también debe tenerse en cuenta.
Los materiales con la misma resistencia a la tracción y a la compresión (como el acero de bajo contenido en carbono) deben adoptar secciones axisimétricas neutras, como circulares, rectangulares, en forma de I, de caja, etc.
De este modo, la tensión máxima de tracción y la tensión máxima de compresión en los bordes superior e inferior de la sección pueden ser iguales.
Para materiales con resistencias a tracción y compresión desiguales (como el hierro fundido, el cemento, etc.), debe adoptarse la forma de sección con el eje neutro inclinado hacia el lado de tracción.
Las vigas mencionadas anteriormente tienen todas la misma sección, y el coeficiente de la sección de flexión es constante, pero en general, el momento flector de cada sección de la viga cambia con la posición de la sección.
El diseño de la sección de una viga recta igual debe realizarse en función del momento flector máximo, y su tensión máxima se aproxima a la tensión admisible.
El momento flector en otras secciones es pequeño, por lo que la tensión es pequeña, y el material no se aprovecha al máximo.
Para ahorrar materiales y reducir el peso propio, el tamaño de la sección puede modificarse de modo que el coeficiente de la sección de flexión cambie con el momento flector.
Se utiliza una sección mayor cuando el momento flector es mayor, mientras que se utiliza una sección menor cuando el momento flector es menor.
Este tipo de viga cuya sección cambia a lo largo del eje se denomina viga de sección variable.
Si la tensión normal máxima en cada sección transversal de una viga de sección variable es igual e igual a la tensión admisible, se denomina viga de igual resistencia.
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
AR 
DE 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO