¿Cómo soporta una viga de acero el peso de un puente o la presión de una grúa? Este artículo profundiza en los cálculos de resistencia a la flexión del acero de sección, explicando los conceptos de etapas elástica, elástico-plástica y plástica. Al comprender la resistencia y rigidez de las distintas secciones, los lectores aprenderán a garantizar la seguridad y estabilidad de las estructuras bajo diversas cargas. Sumérjase para comprender los principios fundamentales que hacen que nuestras construcciones se mantengan erguidas y resistentes.
1. Concepto:
Soporta cargas laterales como vigas de forjado, vigas de grúa, correas, puentes, etc.
2. Clasificación:
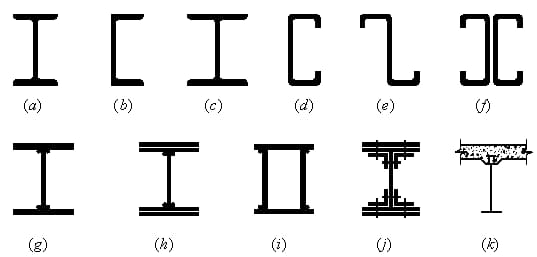
(1) Web sólida：
Perfil de acero en forma de H: Fácil de procesar, sencillo de fabricar y de bajo coste.
Sección compuesta: Cuando el acero en forma de H no puede cumplir los requisitos de resistencia y rigidez.
(2) Estructura reticular:
Cuando la envergadura supera los 40 m, es mejor utilizar una celosía.
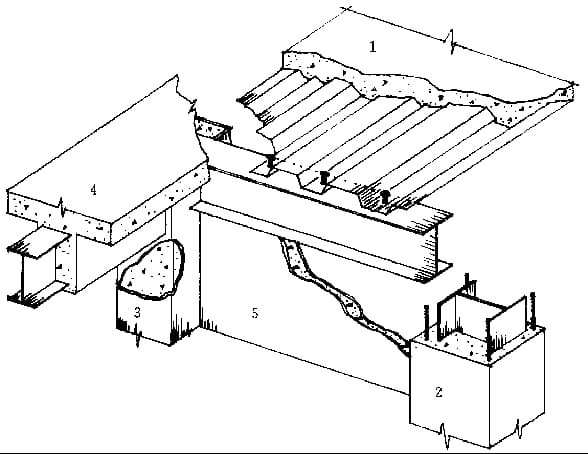
3. Rejilla de vigas:
Sistema plano compuesto por vigas principales y secundarias que se cruzan vertical y horizontalmente.
(1) Red de haces simplificada: Haz principal único.
(2) Parrilla de vigas ordinarias: Dividida en vigas principales y secundarias.
(3) Rejilla de vigas compuestas: Dividida en vigas principales, vigas secundarias horizontales y verticales.
4. Interacción entre vigas y placas:
(1) Co-working: Forjado compuesto.
(2) Obra no cooperativa: Losa general de hormigón armado.
El desarrollo de la tensión normal en la sección transversal puede dividirse en tres etapas:
(1) Fase elástica: Bajo carga dinámica.
(2) Fase elástico-plástica: Bajo carga estática o carga dinámica indirecta.
(3) Etapa de plástico:
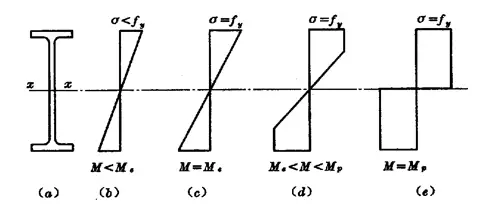
Capacidad de flexión durante la fase elástico-plástica de una sección transversal:
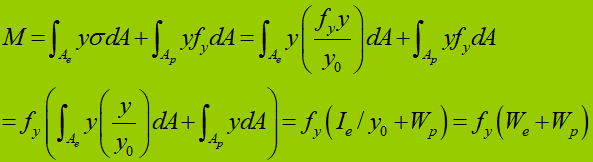
Para una sección rectangular:
(1) Etapa elástica:
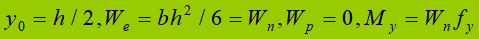
(2) Escenario de plástico:
(3) Fase elástico-plástica:
Factor de forma de la sección:
Desarrollo plástico de sección parcial (1/4 de sección, a = h/8) como estado límite:
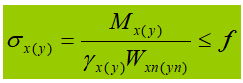
En la fórmula:
γ es el factor de seguridad parcial para el momento, que puede determinarse basándose en la tabla 5.1 de la sección 5 del código de diseño.
Hay dos casos en los que el factor de seguridad parcial para el momento debe tomarse como 1,0.
Método:
S:
La resistencia al cizallamiento puede calcularse utilizando la teoría del flujo de cizallamiento, suponiendo que se distribuye uniformemente a lo largo de la dirección del espesor de la pared delgada.
(1) Al calcular el esfuerzo cortante vertical en cualquier punto del alma, es necesario calcular el momento de inercia de área de la sección bruta por encima o por debajo de dicho punto con respecto al eje neutro x.
(2) Al calcular el esfuerzo cortante horizontal en cualquier punto del ala, es necesario calcular el momento de inercia de área de la sección bruta a la izquierda o a la derecha de dicho punto con respecto al eje neutro x.
Dónde tw es el espesor de la sección en el lugar donde se calcula el esfuerzo cortante.
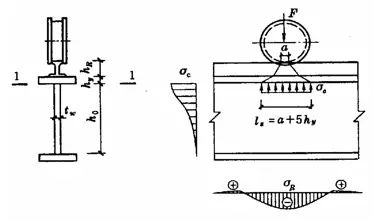
Cuando el ala de una viga está sometida a una gran carga central fija (incluidas las reacciones de los apoyos) y no se dispone de rigidizadores según la Figura 5-5 (a), o cuando está sometida a una carga concentrada móvil (como la presión de las ruedas de la grúa) según la Figura 5-5 (b), debe calcularse la resistencia a compresión local en el borde de la altura del alma. Suponiendo que la carga concentrada se propaga desde el punto de aplicación hasta un rango de altura de hy en una proporción de 1:2,5, y se extiende en una proporción de 1:1 dentro de un rango de altura de hRse distribuye uniformemente sobre la altura de la banda cálculo de bordes. La σ resultantec está muy próxima a la presión local teórica máxima. La resistencia local a la compresión puede calcularse mediante la siguiente fórmula:
En la fórmula,
Cuando el cálculo no es satisfactorio, el soporte o la carga concentrada fija puede reforzarse colocando rigidizadores transversales o modificando el tamaño de la sección. Sin embargo, cuando se soportan cargas concentradas móviles, sólo puede modificarse el tamaño de la sección.
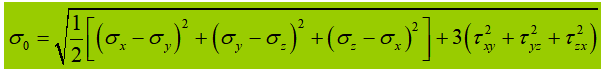
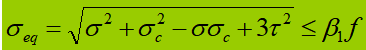
Cuando el vibrador abdominal está sometido a una tensión normal significativa, a una tensión de cizallamiento o a una tensión de compresión local en la altura calculada, es necesario calcular la tensión equivalente en ese lugar.
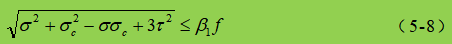
En la fórmula:
σ, τ, σc - tensión normal de flexión, tensión de cizalladura y tensión de compresión local en el mismo punto de la altura de cálculo de la placa abdominal, positiva para la tensión de tracción y negativa para la tensión de compresión;
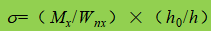
β1 - coeficiente para aumentar el valor de cálculo de la resistencia a la compresión en un punto local. Cuando σ y σc tienen el mismo signo o σc=0, β1=1,1; cuando σ y σc tienen signos opuestos, β1=1.2.
Fenómeno de inestabilidad global:
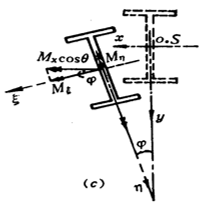
Análisis del mecanismo:
Después de que la viga se deforme por flexión, el ala superior se somete a compresión. Debido a la insuficiente rigidez lateral de la viga, ésta experimentará una deformación lateral por pandeo. La deformación por flexión en el plano causada por el momento también se produce junto con la deformación por torsión debida a la flexión desigual de la parte superior a la inferior de la sección de la viga.
Por lo tanto, la inestabilidad global de la viga adopta la forma de pandeo por flexión y torsión, o más exactamente, pandeo por flexión lateral y torsión.
(1) C1, C2, C3 - En función del tipo de carga
(2) Iy, Iw, It - Momento de inercia de la sección transversal
(3) L - Longitud no arriostrada en dirección lateral
(4) a - Localización del punto de acción en la dirección de la altura.
(5) 
| Condición de carga | Coeficiente | ||
| G | C2 | G | |
| Carga concentrada en la mitad del vano | 1.35 | 0.55 | 0.41 |
| Carga uniformemente distribuida en toda la envergadura | 1.13 | 0.46 | 0.53 |
| Pura flexión | 1.00 | 0.00 | 1.00 |
Los principales factores que afectan a la estabilidad general de las vigas de acero son:
(1) La longitud no arriostrada en la dirección lateral o la distancia L1 entre el punto de apoyo lateral del ala comprimida. Cuanto menor sea el valor de L1, mayor será la estabilidad global de la viga y mayor el momento flector crítico.
(2) El tamaño de la sección transversal, incluidos los distintos momentos de inercia. Cuanto mayor sea el momento de inercia, mayor será la estabilidad global de la viga. En particular, el aumento de la anchura del ala comprimida b1 también puede aumentar el valor de βy en la fórmula.
(3) Las limitaciones de la sección por los apoyos extremos de la viga. Si se pueden mejorar las restricciones a la rotación alrededor del eje y de la sección, la estabilidad global de la viga mejorará considerablemente.
(4) Tipo de carga: Flexión pura, carga uniformemente distribuida, carga concentrada en la mitad del vano.
(5) La localización del punto de acción de la carga a lo largo de la dirección de la altura de la sección transversal, un valor; negativo para el ala superior y positivo para el ala inferior.
Flexión en un solo plano:
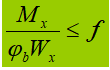
1. Sección soldada en forma de I, biaxialmente simétrica, pura carga de flexión.
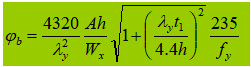
2. Sección soldada en forma de I, uniaxialmente simétrica (efectos de la sección asimétrica y diferentes cargas)
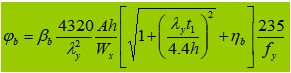
Si φb>0,6, el coeficiente de estabilidad se toma como:
3. Viga de acero laminado ordinario en forma de I simplemente apoyada.
4. Viga simplemente apoyada de canal de acero laminado en caliente.
5. Una viga en voladizo en forma de I de doble eje de simetría.
El ala comprimida de la viga se cubre con un entablado (hormigón armado o chapa de acero) y firmemente unidas para evitar el desplazamiento lateral de la brida comprimida.
Para vigas en H o en I simplemente apoyadas, la relación entre la longitud libre L1 y la anchura b del ala comprimida no supera el valor especificado en la tabla 5.4.
Tabla 5.4: Valor máximo de L1/b1 para el que no se requiere cálculo de estabilidad global para vigas en H o en I simplemente apoyadas.
| Calidad del acero | Una viga sin puntos de apoyo laterales en la mitad del vano. | Viga con un ala sometida a compresión en toda la luz y con puntos de apoyo laterales, independientemente de dónde se aplique la carga. | |
| La carga se aplica a la brida. | La carga se aplica a la brida inferior. | ||
| Q235 | 13.0 | 20.0 | 16.0 |
| Q345 | 10.5 | 16.5 | 13.0 |
| Q39 | 10.0 | 15.5 | 12.5 |
| Q420 | 9.5 | 15.0 | 12.0 |
1. Determinar si se requiere una verificación de estabilidad global.
2. Calcular los parámetros de la sección.
3.Obtener el coeficiente de momento flector crítico equivalente βb en función de las condiciones de carga.
4. Sustituye los valores en las fórmulas para obtener el coeficiente de estabilidad global ϕb, y verifica la estabilidad global.
Ejemplo: 5-2，5-3
Placa de brida: La carga es relativamente sencilla y la estabilidad local se garantiza limitando la relación anchura/espesor de la placa.
Placa web: La carga es compleja y, para cumplir los requisitos de resistencia, la altura de la sección suele ser grande. Si seguimos limitando la relación altura/espesor de la placa del alma, el valor de ésta será muy grande, lo que resulta antieconómico. Por lo tanto, se suelen utilizar rigidizadores para reducir el tamaño de la placa y mejorar la capacidad portante de la estabilidad local.
1. Refuerzos transversales
2. Refuerzos longitudinales
3. Refuerzos cortos
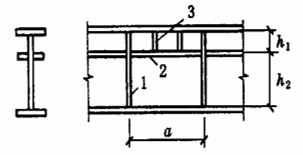
Principio de diseño: principio de igual resistencia.
Según el diseño elástico (con γ=1,0 para no considerar el desarrollo plástico), debido a la influencia de tensión residualla sección transversal real ha entrado en la fase elástico-plástica. La "Especificación" toma Et=0.7E.
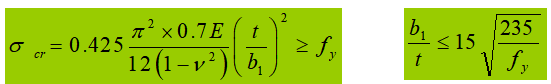
Si se considera el desarrollo plástico (γ > 1,0), el desarrollo plástico será mayor, y Et=0.5E.
| No. | El estado de la placa web. | Especificaciones de la disposición de los rigidizadores | |
| 1 | 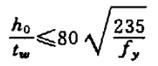 | στ=0 | Se pueden omitir los refuerzos. |
| 2 | στ≠0 | Se recomienda instalar refuerzos transversales que cumplan los requisitos estructurales y de cálculo. | |
| 3 |  | Se recomienda instalar refuerzos transversales que cumplan los requisitos estructurales y de cálculo. | |
| 4 |  La brida comprimida está restringida contra la torsión. | Los rigidizadores longitudinales deben añadirse en la zona de compresión de la sección donde el esfuerzo de flexión es elevado, cumpliendo los requisitos estructurales y de cálculo. | |
| 5 | 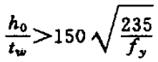 La brida comprimida puede girar libremente. | ||
| 6 | Cuando sea necesario a efectos de cálculo. | ||
| 7 | Cuando la tensión de compresión local es alta. | En caso necesario, deben disponerse rigidizadores cortos en la zona de compresión para cumplir los requisitos estructurales y de cálculo. | |
| 8 | En el soporte de la viga | Es aconsejable instalar refuerzos de soporte que cumplan los requisitos estructurales y de cálculo. | |
| 9 | Cuando el ala está sometida a una gran carga concentrada fija. | ||
| 10 | En cualquier caso |  | |
1. Pandeo de placas compuestas sometidas a esfuerzos
Sólo está configurada la placa de alma con rigidizadores transversales.
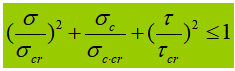
La placa de alma está configurada con rigidizadores transversales y longitudinales al mismo tiempo.
(1) Entre el ala comprimida y los rigidizadores longitudinales.
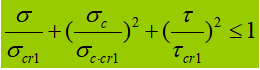
(2) Entre el ala de tracción y los rigidizadores longitudinales.
Los refuerzos transversales cortos se instalan entre el ala comprimida y los refuerzos longitudinales.
2. Requisitos de construcción de los rigidizadores para la placa de alma
(1) Rigidizadores transversales de acero configurados por pares a ambos lados de la placa del alma.
Anchura que sobresale hacia el exterior:
Grosor:
(2) Rigidizadores transversales de acero configurados en un lado de la placa del alma.
Anchura que sobresale hacia el exterior: debe ser superior a 1,2 veces el valor calculado según la fórmula anterior.
Espesor: no debe ser inferior a 1/15 de su anchura saliente hacia el exterior.
(3) En la placa de alma reforzada con rigidizadores transversales y longitudinales, los rigidizadores longitudinales deben desconectarse en sus intersecciones mientras que los rigidizadores transversales permanecen continuos.
El momento de inercia alrededor del eje z también debe satisfacer:
(4) Tratamiento del extremo de los rigidizadores transversales:
3. Refuerzos de apoyo
(1) Cálculo de la estabilidad:
La estabilidad de los rigidizadores de apoyo se calcula como un miembro de compresión sometido a cargas concentradas fijas o a reacciones de apoyo de vigas a lo largo de su eje. El área de la sección transversal A de este miembro de compresión incluye tanto el rigidizador como el área de la placa del alma dentro de 15tw a cada lado del rigidizador. La longitud de cálculo se toma aproximadamente como h0.
(2) Cálculo de la resistencia a la compresión:
El extremo de los rigidizadores de apoyo para viga debe calcularse en función de la carga concentrada fija o reacción de apoyo que soportan. Cuando el extremo de los rigidizadores se recorta plano y ajustado, el esfuerzo de compresión en la cara del extremo debe calcularse como sigue:
donde:
Pasos de diseño para los rigidizadores transversales de la placa de alma:
1. Determine si es necesario instalar barras transversales;
2. Instale los travesaños y determine la separación a, bs, ts;
3. Verificar el estado de tensión compuesto de la placa de alma;
4. Verificación del rigidizador de soporte: incluyendo la soldadura (conexión entre los travesaños y la placa de alma), verificación de la estabilidad a compresión axial (estabilización fuera del plano del eje z) y verificación de la resistencia.
Ejemplo 5-3: Basándose en las condiciones y resultados del Ejemplo 5-2, verifique si la sección de la viga principal mostrada en la Figura 5-9(b) cumple los requisitos. La viga principal es una viga simplemente apoyada en ambos extremos, de acero Q235 y soldada con electrodos de soldadura manual de la serie E43.
Solución:
1. Capacidad de carga de la viga principal:
El diagrama de cálculo simplificado de la viga principal se muestra en la figura 5-9(a). La presión ejercida sobre la viga principal por las vigas secundarias de ambos lados es de 2×73,69+2×2,33=152,04 kN, y la presión de las vigas secundarias del extremo de la viga es la mitad de la de la viga secundaria central.
La reacción en apoyo de la viga principal es R=2×152,04=304,08 kN.
El momento flector máximo de la viga es M=(304,08-76,02)x5-152,04×2,5=760,2 kN.m
2. Calcular las características de la sección:
A=131,2 cm², Ix=145449 cm⁴, Wx=3513,3 cm³. El peso propio de la viga principal es 131,2×10²x7850x10-⁶x1,2=123,6 kg/m=1,211 kN/m. El factor de 1,2 es para considerar el coeficiente aumentado del rigidizador de la viga principal. El valor de cálculo del momento flector después de considerar el peso de la viga principal es M=760,2+1,2×1,211×10²/8=760,2+18,2=778,4 kN-m.
Considerando el valor de cálculo de la fuerza de reacción sobre el apoyo después de tener en cuenta el peso propio de la viga principal es R=304,08+1,2×1,211×10/2=304,08+7,27=311,3kN.
3. Control de resistencia
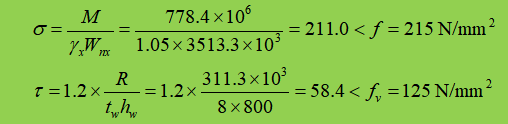
Se proporcionan rigidizadores de apoyo en la conexión de la viga secundaria, y no hay tensión de compresión local. Además, dado que el esfuerzo cortante es relativamente pequeño, no es necesario verificar otros esfuerzos convertidos de la sección.
4. En la viga secundaria hay una placa rígida que garantiza la estabilidad de la viga secundaria y puede servir de punto de apoyo lateral para la viga principal.
En este punto, dado que l1/b1=2500/240=10,4<16, la estabilidad global puede garantizarse sin cálculos.
5. Comprobación de la rigidez
El valor total normalizado de la carga transmitida por la viga secundaria es FT=(15.5+0.52)×7.5=120.2kN, therefore,
El valor total normalizado de la carga transmitida por la viga secundaria es FQ=2.5×4.2×7.5=78.75kN, therefore,
6. Estabilidad local
Brida: b/t=(120-4)/14=8,3<13, que cumple el requisito de estabilidad local, y γx puede tomarse como 1,05; Placa de alma: h0/tw=800/8=100, es necesario prever refuerzos transversales, se omiten los detalles.
Tras el pandeo de la placa delgada, se generan tensiones de tracción transversales en el centro de la placa, lo que restringe aún más la deformación por flexión longitudinal de la placa, permitiéndole seguir soportando una mayor presión.
1. Capacidad portante a cortante tras pandeo: Fórmula (5-94)
2. La capacidad portante a cortante incluye dos partes: Fuerza cortante de pandeo (resistencia al pandeo) + fuerza cortante en el campo de tensión (resistencia después del pandeo).
3. Fuerza de cizallamiento del campo de tensión:
(1) Método del campo de tensión (complejo);
(2) Especificación del código.
Teniendo en cuenta que la capacidad portante a flexión de la placa de alma disminuye ligeramente tras el pandeo.
Dos supuestos:
(1) Altura efectiva;
(2) Simetría entre la zona de tensión y la zona de compresión.
La fórmula para calcular la capacidad portante:
En la fórmula,
Esto indica que:
(1) Cuando M en la sección es inferior a Mf que puede soportar el ala, la chapa del alma puede soportar la fuerza cortante Vu;
(2) Cuando V en la sección es inferior a 0,5Vu, tomar M = Meu.
(1) Si los rigidizadores de apoyo por sí solos no pueden satisfacer la Ecuación (5.99), se deben añadir rigidizadores transversales pareados a ambos lados del alma para reducir la longitud de la región de pandeo.
(2) Las dimensiones de la sección transversal de los rigidizadores transversales deben cumplir los requisitos de construcción para los rigidizadores del alma según la Ecuación 5.85.
(3) De acuerdo con las especificaciones de la estructura de acero, el rigidizador transversal central debe tratarse como un miembro de compresión axial y su estabilidad fuera del plano del alma debe calcularse basándose en la fuerza axial utilizando la siguiente fórmula:
Cuando el rigidizador está sometido a una carga transversal concentrada F, Ns debe incrementarse en F.
Calcular el valor de cálculo del momento flector máximo Mmax para la viga en función de las condiciones reales.
Determinar el módulo de sección necesario en función de la resistencia a la flexión y la estabilidad general:
Determine la sección de acero basándose en las tablas de secciones.
Verificación de la sección:
(1) Verificación de la resistencia: flexión, cizalladura, compresión local y tensión equivalente.
(2) Verificación de la rigidez: verificar la relación entre la deformación y la luz de la viga.
(3) Verificación de la estabilidad global (la estabilidad local de la sección de acero no suele requerir verificación).
(4) Ajuste la sección en función de los resultados de la verificación y vuelva a realizar la verificación hasta que cumpla los requisitos de diseño.
1) Determinar el módulo de sección necesario en función de las condiciones de carga.
2) Determinar la altura de la viga:
Altura seleccionada: hmin ≤ h ≤ hmax.
3). Determinar el espesor del alma (suponiendo que todos los esfuerzos cortantes son soportados por el alma), entonces:
Alternativamente, el espesor de la banda puede determinarse utilizando fórmulas empíricas:
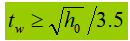
4). Determinar la anchura de la brida:
Una vez determinado el espesor del alma, el área del ala Af puede determinarse en función de los requisitos de resistencia a la flexión. Tomando como ejemplo una sección en forma de I:
Una vez Af se determina, se puede seleccionar b o t para determinar el otro valor.
5). Verificación de la sección:
6). Cálculo de las soldaduras entre el alma y el ala
La soldadura de conexión se utiliza principalmente para resistir cizalladura por flexióny el cizallamiento por unidad de longitud es:
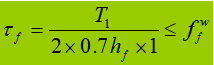
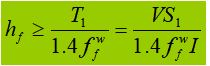
Cuando la viga está sometida a una carga concentrada fija sin rigidizadores de apoyo, la soldadura del ala superior soporta tanto el esfuerzo cortante T1 y la fuerza concentrada F. La fuerza por unidad de longitud generada por F es V1:
Propósito: Para ahorrar acero y hacer frente a los cambios del momento flector.
Métodos de cambio de sección:
Puntos a tener en cuenta:
1. Clasificación:
2. Métodos de empalme para perfiles de acero laminado:
3. Técnicas de empalme de vigas compuestas:
Consideraciones clave:
1. Conexiones primarias y secundarias de vigas de acero:
2. Tipos de soporte de vigas:
Consideraciones clave sobre el diseño:
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
AR 
DE 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO