¿Alguna vez ha tenido problemas para calcular la distancia entre ejes de los rodillos de una máquina? En esta entrada del blog, exploraremos un método sencillo para determinar esta medida crucial. Nuestro experto ingeniero mecánico le guiará a lo largo del proceso, proporcionándole valiosas ideas y ejemplos prácticos. Al final, tendrá una idea clara de cómo abordar este desafío común y mejorar sus habilidades de diseño de máquinas.
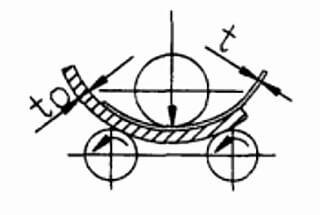
En la fabricación de calderas y recipientes a presión, la tecnología de conformado es uno de los principales procesos de fabricación.
En el proceso de conformado, el laminado de la sección del cilindro es el método de conformado más básico. El laminado requiere mucho trabajo. La mayor parte del proceso de conformado se lleva a cabo en una laminadora simétrica de tres rodillos. Sin embargo, debido a que el grosor y el diámetro de la sección del cilindro se determinan en función de las diferentes condiciones del proceso de producción, existe un número considerable de especificaciones y variedades.
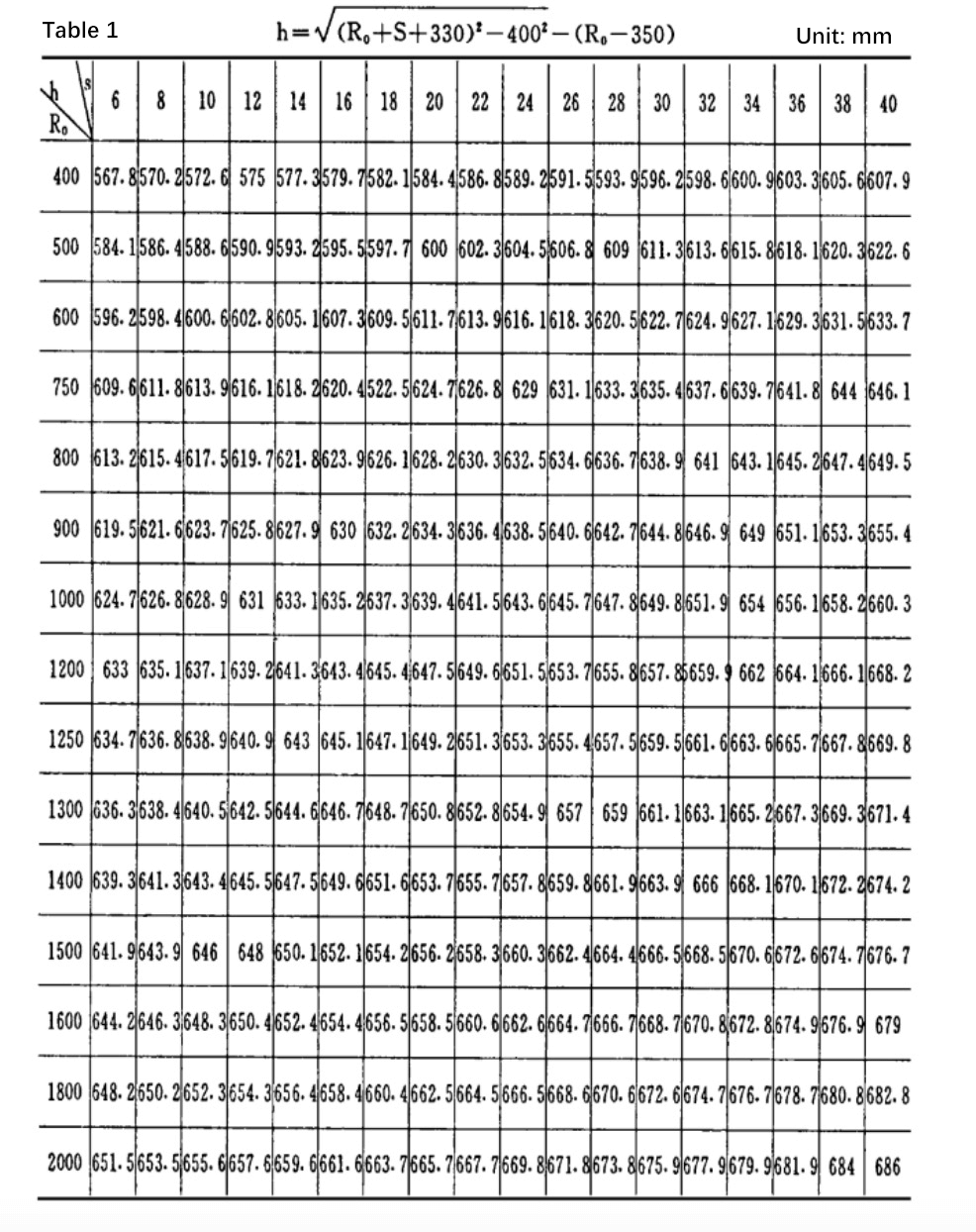
La precisión de la curvatura tras el conformado depende del parámetro "H", que es la distancia central entre los rodillos superior e inferior al final del laminado.
Este parámetro suele determinarse mediante la fórmula (1).
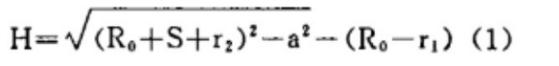
Puede parecer que esta fórmula no es complicada, pero para los fabricantes, la carga de trabajo acumulada es considerable debido a las distintas especificaciones y variedades de secciones de cilindros.
Para simplificar y facilitar la determinación del valor de "H" en diferentes condiciones, este artículo utilizará los dos algoritmos gráficos siguientes.
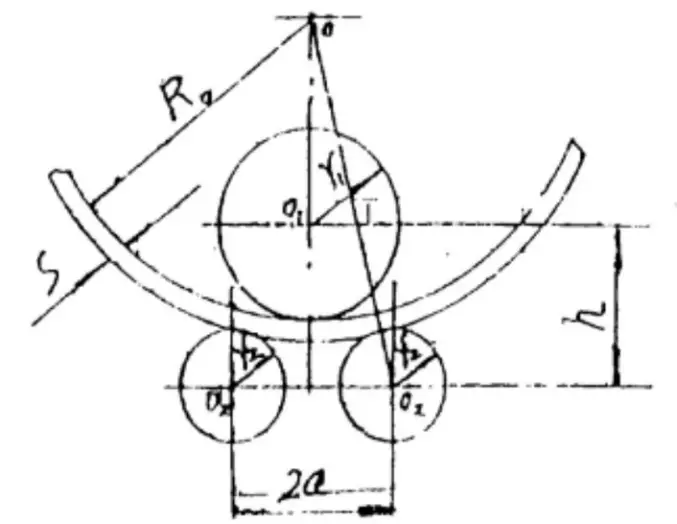
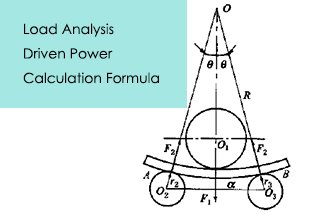
Fig. 1 Diagrama de posición final de tres rodillos simétricos máquina curvadora de chapas
Cuando un determinado tipo de laminadora de chapa los parámetros a, r1 y r2 en la fórmula anterior son constantes, sólo s y R0 son variables.
Por lo tanto, cuando un determinado tipo de máquina curvadora de chapas se utiliza para enrollar cualquier espesor y radio de curvatura, el correspondiente parámetro principal "h" puede obtenerse mediante el siguiente algoritmo gráfico.
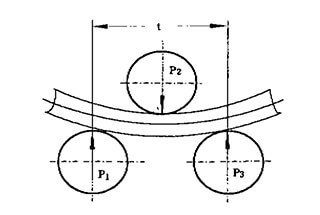
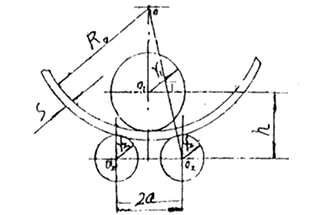
En primer lugar, se establece un sistema de coordenadas rectangulares con a como ordenada y h como abscisa.
A continuación, se realiza el siguiente dibujo en el sistema de coordenadas (mostrado en la Fig. 2)
Debe interceptar OP = a en el eje longitudinal, tomar el punto P como centro del círculo y tomar (R0 + S + r2) como radio para hacer un punto positivo a en el eje transversal de la intersección del arco.
Debe tomar el punto a como centro del círculo, tomar R0 como radio, e inverso como punto B en el eje transversal del arco.
Entonces se toma el punto B como centro del círculo y R1 se toma como radio de la intersección del arco, y se hace un punto C en la dirección positiva del eje transversal del arco.
Por lo tanto: OC = h.
Por ejemplo,
Las secciones de tambor con S = 20 mm y d = 2 000 mm se laminan en una máquina curvadora de chapas de tres rodillos simétricos de 70 × 4000.
Para calcular el valor de h.
Según los datos, R1 = 350mm, R2 = 330 mm, 2a = 800 mm.
Según el algoritmo gráfico (mostrado en la Fig. 2): h = 640mm, que se calcula mediante la fórmula:
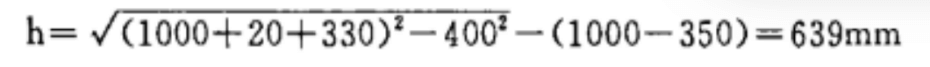
El error absoluto es de sólo 1 mm, lo que representa 0,015% del valor real, lo que es suficientemente preciso.
Si (R + S + r) se convierte en una regla móvil, resulta más cómodo.
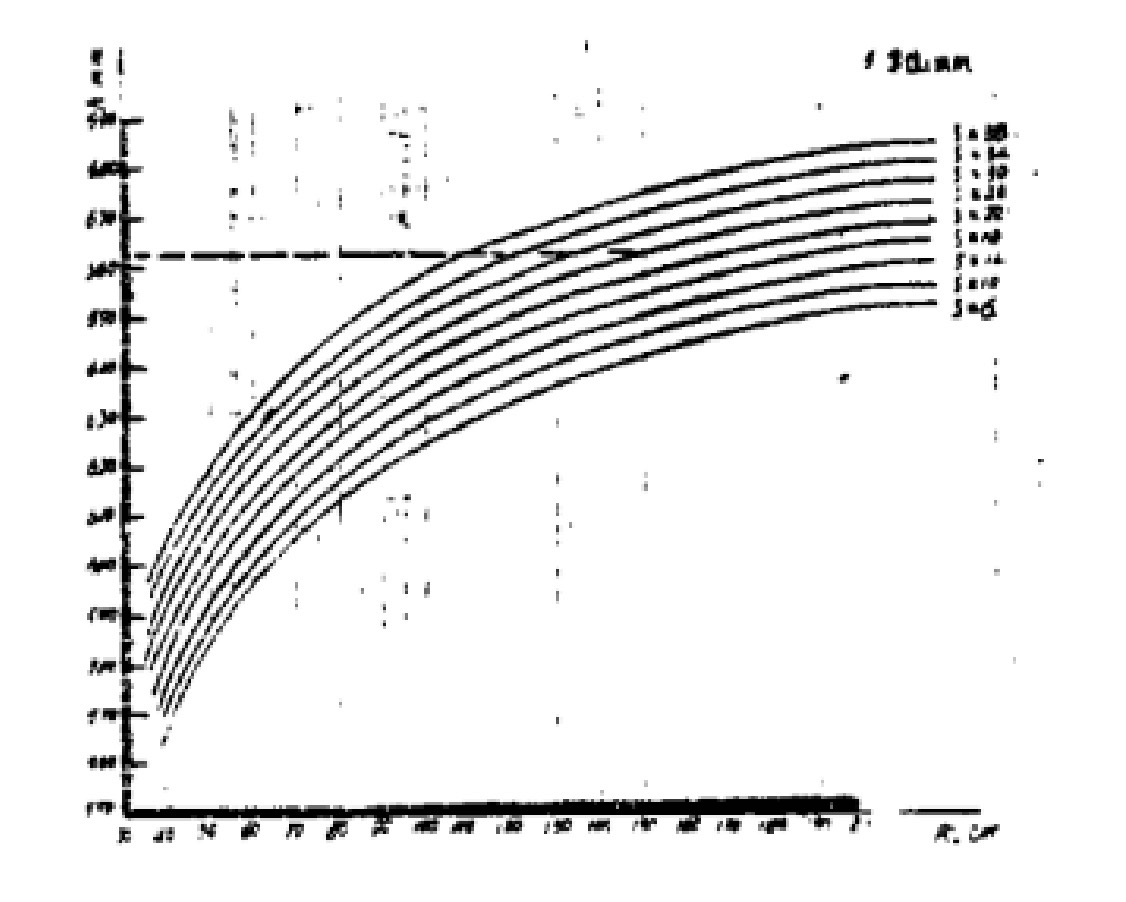
Fig. 2 Normograma para calcular "h"
Como ya se sabe, cuando un determinado tipo de flexión sus parámetros a, R1 y R2 son fijos.
Entonces, si la curva de relación de R0 y h bajo diferentes espesores de placa se dibuja en r0-h, el gráfico del punto común de R0 y h de chapa de acero de diferentes espesores en este tipo de maquinaria de laminación puede obtenerse.
Es muy conveniente obtener el valor del parámetro principal "h" de la sección del tambor en este tipo de máquina curvadora de chapa en todas las condiciones diferentes.
A continuación se muestra un diagrama de punto común de un tres simétrico de 70 × 4000 placa de rodillo dobladora.
Conocido: r1 = 350 mm, r2 = 330mm, a = 400mm
Así que..:
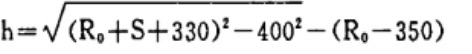
La tabla 1 es la tabla de datos de cálculo y dibujo con un intervalo s de 2 mm.
Según la experiencia práctica, el grosor del maquinaria de laminación es generalmente de 6 ≤ s ≤ 40 (mm).
Generalmente, el radio de la sección del tambor de laminación es de 400 ≤ R0 ≤ 200 (mm).
Por lo tanto, este intervalo se utiliza como intervalo de dibujo de cálculo.
De la tabla 1 se desprende que el valor de "n" equivale básicamente al espesor de chapa s cuando se utiliza un determinado tipo de máquina curvadora de chapas para enrollar una determinada cantidad de R0.
El error entre el valor real y el valor real es inferior a 0,05%.
Sin embargo, cuando se dobla la placa de cobre, se producen tanto deformaciones plásticas como elásticas.
Por lo tanto, habrá una cierta recuperación elástica después de la descarga.
Por lo tanto, en la producción real, el valor debería ser ligeramente inferior al real.
De esta forma, si utilizamos la ley del cambio equivalente de los dos, el dibujo se simplificará y el elástico springback después de la flexión real se puede compensar.
Al mismo tiempo, la línea del gráfico puede reducirse, y el valor "h" correspondiente a cualquier S puede determinarse bajo un determinado R0.
El primer algoritmo gráfico es universal, mientras que el segundo es para un determinado tipo de máquina curvadora de chapa, cuyo tipo de máquina curvadora de chapa corresponde a un (k-R0-S) gráfico de copuntos.
Los resultados de los dos algoritmos de grafos en la enseñanza son muy buenos e ilustran mucho a los alumnos.
En particular, este último método tiene cierta viabilidad.
Se sugiere que el fabricante de la máquina curvadora de chapa configure el diagrama principal común de (n-R0-S) en el maquinaria de laminación o en el manual, lo que aportará una gran comodidad a la producción real del fabricante.
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
DE 
FR 
IT 
NL 
PT 
RU 