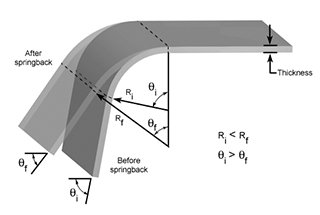
¿Alguna vez se ha preguntado por qué algunas piezas metálicas rebotan después de doblarse? En este artículo, exploraremos el fascinante mundo de las matrices de plegado y cómo predecir con precisión el springback. Aprenderá consejos prácticos y fórmulas para conseguir resultados precisos en sus proyectos metalúrgicos.
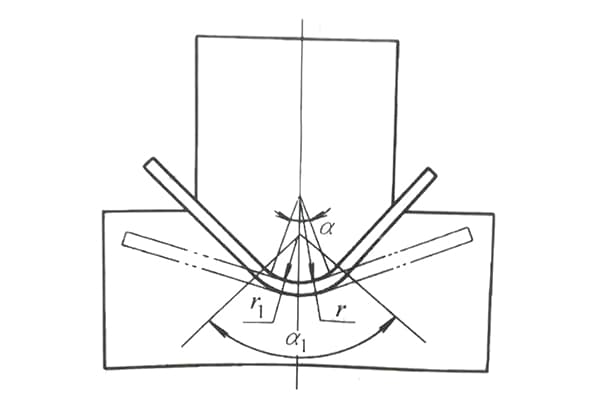
Al diseñar una matriz de doblado con un arco interno, la precisión y el comportamiento del material son factores críticos que a menudo se pasan por alto en los enfoques convencionales. Muchos diseñadores ignoran por completo el springback utilizando el mismo radio (R) que el producto acabado o aplican un factor de reducción rudimentario al valor R sin tener en cuenta las complejidades de las propiedades y geometrías de los materiales.
Por ejemplo, una práctica habitual para un producto con un valor R original de 1 mm implica reducir el radio del molde convexo en un factor de 0,8 para materiales más duros o de 0,9 para materiales más blandos. Este enfoque simplista, aunque a veces resulta eficaz para aplicaciones básicas, carece de los matices necesarios para especificaciones más exigentes.
Las limitaciones de este método se hacen especialmente evidentes cuando se trata de materiales finos y radios grandes. Consideremos un producto con un grosor de 0,5 mm y un radio interno de 200 mm. En estos casos, predecir con exactitud el springback se convierte en un reto debido a la compleja interacción entre las propiedades del material, la relación grosor-radio y el ángulo de flexión.
Para abordar estas limitaciones y mejorar la precisión en el diseño de matrices, es necesario un enfoque más sofisticado. En la siguiente sección se presenta una fórmula universal de springback que tiene en cuenta diversos parámetros geométricos y de material, lo que permite realizar cálculos más precisos basados en entradas numéricas. Este método proporciona una base sólida para el diseño de matrices en una amplia gama de aplicaciones y materiales.
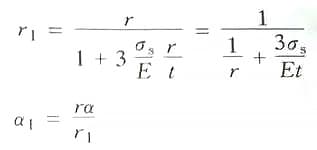
En la fórmula:
Suponiendo 3σs/E=A como coeficiente de simplificación, cuyos valores figuran en la Tabla 2-27. La fórmula de cálculo del radio de la esquina de la matriz convexa durante la flexión de barras de sección circular es la siguiente:

El valor de A se indica en la tabla siguiente.
| Ciencia de los materiales | Estado | A | Ciencia de los materiales | Estado | A |
| 1035(L4) 8A06(L6) | recocido | 0.0012 | QBe2 | suave | 0.0064 |
| Dureza en frío | 0.0041 | duro | 0.0265 | ||
| 2A11(LY11) | suave | 0.0064 | QA15 | duro | 0.0047 |
| duro | 0.0175 | 08, 10, Q215 | 0.0032 | ||
| 2A12(LY12) | suave | 0.007 | 20, Q235 | 0.005 | |
| duro | 0.026 | 30, 35, Q255 | 0.0068 | ||
| T1, T2, T3 | suave | 0.0019 | 50 | 0.015 | |
| duro | 0.0088 | T8 | recocido | 0.0076 | |
| H62 | suave | 0.0033 | dureza al frío | ||
| semiduro | 0.008 | ICr18N9Ti | recocido | 0.0044 | |
| duro | 0.015 | dureza al frío | 0.018 | ||
| H68 | suave | 0.0026 | 65Mn | recocido | 0.0076 |
| duro | 0.0148 | dureza al frío | 0.015 | ||
| QSn6,5-0,1 | duro | 0.015 | 60Si2MnA | recocido | 0.125 |
Si los materiales necesarios no están disponibles arriba, también puede consultar la tabla siguiente para encontrar el módulo de elasticidad y el límite elástico del material, y luego sustituirlos en la fórmula anterior para el cálculo.
| Nombre del material | Calidad del material | Estado del material | Fuerza máxima | Velocidad de elongación(%) | Límite elástico/MPa | Módulo elásticoE/MPa | |
| resistencia al cizallamiento/MPa | tracción/MPa | ||||||
| Acero estructural al carbono | 30 | Normalizado | 440-580 | 550-730 | 14 | 308 | 22000 |
| 55 | 550 | ≥670 | 14 | 390 | – | ||
| 60 | 550 | ≥700 | 13 | 410 | 208000 | ||
| 65 | 600 | ≥730 | 12 | 420 | – | ||
| 70 | 600 | ≥760 | 11 | 430 | 210000 | ||
| Acero estructural al carbono | T7~T12 T7A-T12A | Recocido | 600 | 750 | 10 | – | – |
| T8A | Endurecido en frío | 600-950 | 750-1200 | – | – | – | |
| Acero al carbono de alta calidad | 10Mn2 | Recocido | 320-460 | 400-580 | 22 | 230 | 211000 |
| 65M | 600 | 750 | 18 | 400 | 211000 | ||
| Acero estructural aleado | 25CrMnSiA 25CrMnSi | Recocido a baja temperatura | 400-560 | 500-700 | 18 | 950 | – |
| 30CrMnSiA 30CrMnSi | 440-600 | 550-750 | 16 | 1450850 | – | ||
| Acero para muelles de alta calidad | 60Si2Mn 60Si2MnA 65Si2WA | Recocido a baja temperatura | 720 | 900 | 10 | 1200 | 200000 |
| Endurecido en frío | 640-960 | 800-1200 | 10 | 14001600 | – | ||
| Acero inoxidable | 1Cr13 | Recocido | 320-380 | 400-170 | 21 | 420 | 210000 |
| 2Cr13 | 320-400 | 400~500 | 20 | 450 | 210000 | ||
| 3Cr13 | 400-480 | 500~600 | 18 | 480 | 210000 | ||
| 4Cr13 | 400-480 | 500-500 | 15 | 500 | 210000 | ||
| 1Cr18Ni9 2Cr18Ni9 | Tratamiento térmico | 460~520 | 580-610 | 35 | 200 | 200000 | |
| Endurecido en frío | 800-880 | 100-1100 | 38 | 220 | 200000 | ||
| 1Cr18Ni9Ti | Reblandecido con tratamiento térmico | 430~550 | 54-700 | 40 | 240 | 200000 | |
Lo mejor es establecer una base de datos de materiales de uso común y obtener de los proveedores los parámetros físicos que falten. Si los parámetros de módulo elástico y límite elástico son correctos, la flexión y el rebote de los terminales generales de los muelles, las piezas de aspecto y los perfiles son más precisos.