¿Alguna vez se ha preguntado cómo calcular con precisión la fuerza de flexión necesaria para la fabricación de chapas metálicas? En esta interesante entrada del blog, exploraremos los entresijos del cálculo de la fuerza de flexión, basándonos en la experiencia de ingenieros mecánicos experimentados. Descubra los factores clave que influyen en la fuerza de flexión y aprenda a aplicar fórmulas probadas para optimizar sus procesos de conformado de metales. Prepárese para elevar sus conocimientos sobre plegado de chapa metálica a nuevas cotas.
En la actualidad, las fórmulas para calcular la fuerza de flexión que se utilizan de forma generalizada se han adoptado de fuentes extranjeras sin ninguna información sobre su origen o ámbito de aplicación.
Este artículo presenta un análisis sistemático del proceso de derivación de la fórmula para calcular la fuerza de flexión, así como los parámetros necesarios.
Además, se introduce un nuevo enfoque para calcular la fuerza de flexión con el fin de ampliar su ámbito de aplicación.
Calcular la fuerza de plegado de las chapas metálicas es esencial para conseguir procesos de plegado precisos y eficaces. Comprender estos cálculos ayuda a seleccionar las herramientas adecuadas y a garantizar la calidad de los plegados. Este capítulo ofrece una visión general de los conceptos clave, herramientas y consejos prácticos para calcular la fuerza de plegado en trabajos de chapa metálica.
El cálculo de la fuerza de plegado es crucial en el trabajo de chapa metálica para garantizar que se aplica la cantidad correcta de fuerza durante el proceso de plegado. De este modo se evitan pérdidas de material y daños en las herramientas, y se garantiza la calidad de plegado deseada. Unos cálculos precisos ayudan a seleccionar la plegadora y el utillaje adecuados, lo que se traduce en una producción eficiente y un ahorro de costes.
La fuerza de flexión ( F ) necesaria para doblar una chapa puede calcularse mediante la fórmula:
donde:
El radio interno ( R ) de la curva suele aproximarse en función de la abertura de la matriz ( V ):
La abertura de la matriz ( V ) se selecciona en función del grosor de la chapa ( S ):
La longitud mínima de la pestaña garantiza que el material no se caiga durante el proceso de plegado y se calcula teniendo en cuenta la apertura de la matriz y el ángulo de plegado.
En los últimos años, la máquina plegadora se ha generalizado en diversos sectores y ha ampliado su capacidad de procesamiento.
A pesar de su popularidad, ha habido una falta de discusión sistemática sobre el cálculo de la fuerza de flexión.
En la actualidad, existen aproximadamente dos tipos de fórmulas de cálculo de la fuerza de flexión recomendadas por los manuales de producto de diferentes fabricantes de prensas plegadoras.
En la fórmula:
La fórmula recomendada por el fabricante para calcular la fuerza de flexión se basa en una fórmula mencionada anteriormente.
Ambas fórmulas se han extraído de diversos folletos de productos, pero no hay pruebas de su exactitud.
Calculadora relacionada: Calculadora de tonelaje de prensas plegadoras
La figura 1 es una representación esquemática del proceso de plegado de una hoja.
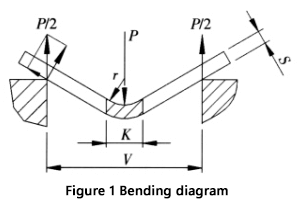
El cálculo de la fuerza de flexión y sus parámetros se explican a continuación:
La anchura recomendada de la abertura inferior de la matriz (V) para el plegado libre es de 8 a 10 veces el espesor de la chapa (S), con una relación anchura/espesor de V/S = 9.
Los fabricantes de plegadoras proporcionan los valores de la anchura de la matriz (V) y el radio interior (r) de la pieza plegada en su tabla de parámetros de fuerza de plegado. La relación radio-anchura suele ser r = (0,16 a 0,17) V, y en este caso se utiliza el valor de 0,16.
Durante el proceso de plegado, el material de la zona de deformación sufre una importante deformación plástica, lo que provoca que se doble alrededor de la línea central.
En algunos casos, pueden aparecer pequeñas grietas en la superficie exterior de la zona curva.
La tensión en la zona de deformación, excepto cerca de la capa central, es cercana a la resistencia a la tracción del material, con la parte superior de la capa neutra comprimida y la parte inferior en tensión.
La figura 2 ilustra la sección transversal y el diagrama de tensiones correspondiente en la zona de deformación.
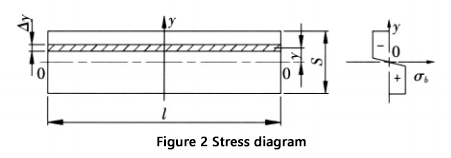
El momento flector en la sección de la zona de deformación es:
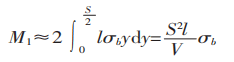
El momento flector producido por la fuerza de flexión en la zona de deformación se representa en la figura 1.
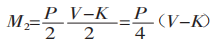
De M1 = M2, obtenemos:
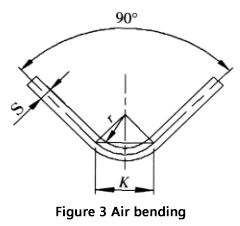
Al doblar una chapa con un molde universal en una máquina dobladora, como se muestra en la figura 3, la mayoría de las chapas se doblan a 90°. En este caso, K es:
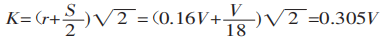
Sustituyendo K en la ecuación (1), obtenemos:
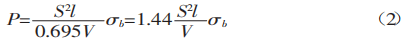
La resistencia a la tracción de los materiales ordinarios, σb, es de 450 N/mm². Este valor puede utilizarse en la fórmula (2) para calcular el resultado.
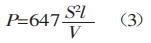
La fórmula para calcular la fuerza de flexión obtenida aquí coincide con la información facilitada en folletos extranjeros.
Las variables de la fórmula son:
Como se desprende del proceso de derivación, cuando se utilizan las fórmulas (2) o (3) para calcular la fuerza de flexión, es importante asegurarse de que se cumplen dos condiciones adicionales: la relación entre la anchura y el grosor (V/S) debe ser igual a 9, y la relación entre el radio y la anchura debe ser igual a 0,16.
Si no se cumplen estas condiciones, pueden producirse errores importantes.
El cálculo de la fuerza de flexión puede complicarse cuando no es posible cumplir los dos requisitos adicionales (relación anchura/espesor V/S = 9 y relación radio/anchura = 0,16) debido a limitaciones de diseño o proceso.
En tales situaciones, es aconsejable seguir estos pasos:
Estos pasos proporcionarán un resultado más preciso y fiable en comparación con el uso de la fórmula comúnmente utilizada. En la Figura 4 se muestra un ejemplo para ilustrar este proceso.
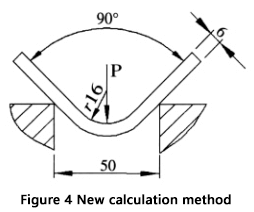
Dadas: Espesor de la chapa (S) = 6mm, Longitud de la chapa (l) = 4m, Radio de curvatura (r) = 16mm, Anchura de la abertura de la matriz inferior (V) = 50mm, y Resistencia a la tracción del material (σb) = 450N/mm².
Pregunta: ¿Cómo podemos calcular la fuerza de flexión necesaria para la flexión por aire?
Estos son los pasos:
En primer lugar, calcula la relación entre anchura y grosor y la relación entre radio y anchura:
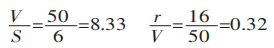
A continuación, calcula la anchura proyectada de la zona de deformación:
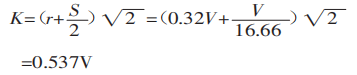
Por último, utilice la fórmula (1) para calcular la fuerza de flexión:
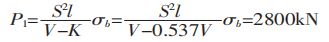
Si se utiliza la fórmula recomendada habitualmente para calcular la fuerza de flexión:
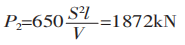
De P1/P2 = 1,5 se deduce que la diferencia entre P1 y P2 es 1,5 veces.
La razón de esta discrepancia se debe a que, en este ejemplo, el radio de curvatura es relativamente grande, lo que se traduce en una mayor superficie deformada y, por tanto, requiere una mayor fuerza de curvatura.
La relación entre radio y anchura en este ejemplo es de 0,32, lo que supera los criterios antes mencionados.
Utilizar la fórmula estándar para calcular la fuerza de flexión no es adecuado para este escenario. Las ventajas de utilizar el nuevo método de cálculo pueden observarse en este ejemplo.
Además, existe una calculadora en línea para calcular la fuerza de flexión con el nuevo método.
Tabla de resistencia a la tracción
| Material | Resistencia a la tracción | ||
|---|---|---|---|
| Americana | Europea | China | N/mm² |
| Aluminio 6061 | Alu50 | LD30 | 290 |
| Aluminio 5052 | Alu35 | LF2 | 303 |
| 1010 Acero dulce | DC01 | 10/10F | 366 |
| A 536 -80 G 60-40-18 | GGG-40 | QT400-18 | 400 |
| A 351 G CF 8 | G-X 6CrNi 18 9 | Q235 | 450 |
| A 572 G50 | S 355 MC | Q345 | 550 |
| Inoxidable 304 | Inox V2A | 0Cr18Ni9 | 586 |
| Acero inoxidable 316 | Inox V4A | 0Cr17Ni12Mo2 | 600 |
| 4140 Baja aleación | 42 CrMo 4 | 42CrMo | 1000 |
Las fórmulas para calcular los parámetros de acuñación son diferentes de las de curvado por aire.
1. Anchura de la uve del troquel:
V = chapa metálica espesor × 5
2. El radio interno viene determinado por la punta del punzón, que debe elegirse de acuerdo con la siguiente fórmula:
Radio = espesor de la chapa × 0.43.
3. Fuerza necesaria para acuñar：
F(kn/m)=Espesor2×1,65×Resistencia a la tracción (N/mm)2)×4,5/Anchura de la uve del troquel
4. La fórmula para calcular el borde interno mínimo sigue siendo la misma:
Canto interno mínimo = Die vee × 0.67
Algunas herramientas necesitan una fuerza particular para ceder la chapa y gestionar el springback con el fin de obtener el perfil requerido.
Como ejemplo consideraremos las herramientas joggle, que hacen dos dobleces a la vez con una distancia corta entre el doblez y el contrapliegue.
Como estas herramientas hacen dos curvas a la vez, springback tiene que ser cancelado completamente por acuñación.
La ecuación para calcular la fuerza necesaria es:
Por lo general, las herramientas de palanca constan de un soporte de inserción en el que se fijan con tornillos prisioneros las herramientas de palanca elegidas en función de la palanca y el ángulo requerido.
Es importante pedir asesoramiento técnico al fabricante antes de comprar, porque estos sistemas sólo pueden doblar chapas finas, de 2 mm como máximo, pero el grosor máximo dependerá del tipo de inserto y podría ser inferior a 2 mm.
A continuación encontrará respuestas a algunas preguntas frecuentes:
La resistencia a la tracción desempeña un papel crucial a la hora de determinar la fuerza de flexión necesaria para las chapas metálicas. La resistencia a la tracción es la tensión máxima que puede soportar un material estirado antes de romperse. Cuando la chapa se dobla, experimenta esfuerzos de tracción y compresión. La superficie exterior de la curva está sometida a un esfuerzo de tracción, mientras que la superficie interior sufre un esfuerzo de compresión.
La fuerza de flexión necesaria está directamente influenciada por la resistencia a la tracción del material, ya que una mayor resistencia a la tracción significa que el material puede soportar una mayor tensión sin fallar. Esto significa que los materiales con mayor resistencia a la tracción necesitan más fuerza para alcanzar el mismo grado de flexión que los materiales con menor resistencia a la tracción.
Para calcular la fuerza de flexión, se considera el esfuerzo de flexión, que está relacionado con la resistencia a la tracción. La fórmula del esfuerzo de flexión
implica el momento flector (M), la distancia del eje neutro a la fibra más externa (c) y el momento de inercia de la sección transversal (I). El momento flector depende de la fuerza aplicada y de la longitud del brazo de palanca. Garantizar que el esfuerzo de flexión no supere la resistencia a la tracción del material es vital para evitar el fallo durante la flexión.
En resumen, una mayor resistencia a la tracción requiere una mayor fuerza de flexión para doblar la chapa metálica sin provocar su rotura, lo que pone de relieve la importancia de tener en cuenta las propiedades del material en los cálculos de la fuerza de flexión.
A la hora de calcular la fuerza de flexión de las chapas metálicas, hay que tener en cuenta varios factores clave para garantizar unos resultados precisos y fiables. Los principales factores que influyen en el cálculo de la fuerza de flexión son:
Las propiedades de los materiales desempeñan un papel crucial, sobre todo la resistencia a la tracción y el límite elástico. La resistencia a la tracción es el esfuerzo máximo que puede soportar un material antes de fallar. Por ejemplo, el aluminio tiene una resistencia a la tracción de 200-300 N/mm², el acero dulce (Q235) oscila entre 370-500 N/mm² y el acero inoxidable ronda los 650-700 N/mm². El límite elástico determina la tensión a la que el material empieza a deformarse plásticamente; un límite elástico más alto requiere más fuerza de flexión.
El grosor del material influye significativamente en la fuerza de flexión, ya que los materiales más gruesos resisten más la deformación, lo que requiere una fuerza mayor. Las fórmulas de cálculo suelen incluir el grosor del material como variable clave.
El radio y el ángulo de curvatura también son importantes. El radio interior de la curva, o el radio de la curva, influye en la fuerza necesaria, ya que los radios más pequeños requieren más fuerza debido a una mayor concentración de tensiones. El ángulo de curvatura influye en la fuerza necesaria, y la mayoría de los cálculos se basan en una curvatura de 90 grados, pero requieren ajustes para ángulos diferentes.
La configuración del utillaje y de la matriz, concretamente la apertura en V de la matriz inferior, afecta a la fuerza de plegado. La anchura del canal inferior de la matriz en la plegadora está relacionada con el grosor del material, y el plegado de precisión puede requerir una abertura en V más estrecha para materiales más finos.
El factor K y la posición del eje neutro también influyen en el proceso de flexión. El factor K, aunque está más directamente relacionado con el cálculo de las tolerancias y deducciones por flexión, afecta al comportamiento general de la flexión y a la fuerza necesaria al determinar dónde el material no se comprime ni se estira.
Por último, el cálculo de la fuerza de flexión suele implicar una fórmula que incorpora la resistencia a la tracción del material, el grosor y la longitud de la curva. Por ejemplo, una fórmula simplificada para el acero bajo en carbono es:
donde ( t ) es el espesor en mm y ( l ) es la longitud en metros, con el resultado en toneladas.
Si tiene en cuenta estos factores, podrá calcular con precisión la fuerza de plegado necesaria para las operaciones de plegado de chapa metálica, asegurándose de que la plegadora está ajustada correctamente para lograr el plegado deseado sin provocar fallos en el material ni una deformación excesiva.
Para determinar los ajustes adecuados de una plegadora, hay que tener en cuenta varios factores clave que garantizan un plegado preciso y eficaz de la chapa. En primer lugar, identifique el tipo y el grosor del material, ya que influyen significativamente en la fuerza de plegado necesaria. Los distintos metales, como el acero inoxidable y el aluminio, tienen distintas resistencias y elasticidad, que afectan a la fuerza necesaria para el plegado.
A continuación, calcule el tonelaje necesario mediante la fórmula ( P=650S²L/V ), donde ( P ) es la fuerza de doblado, ( S ) es el grosor de la placa metálica y ( V ) es la abertura de la matriz inferior. Tenga en cuenta la longitud y el ángulo de plegado, ya que los ángulos más agudos requieren un tonelaje mayor. Asegúrese de que el material está bien sujeto y alineado para evitar desviaciones e imprecisiones.
Los distintos métodos de plegado, como el plegado por aire, el plegado inferior y el acuñado, requieren tonelajes diferentes, siendo el plegado por aire el de referencia y el acuñado el que requiere aproximadamente ocho veces el tonelaje del plegado por aire. Compruebe que el tonelaje no supera el límite de tonelaje central de la plegadora para evitar sobrecargas y posibles daños.
Seleccione el utillaje adecuado que se adapte al material y a los requisitos de plegado, asegurándose de que el utillaje esté correctamente alineado e instalado. Calibre la máquina inspeccionándola y limpiándola, ajustando el calibrador trasero y calibrando la posición y el ángulo del cilindro. Programe la prensa plegadora de acuerdo con el tonelaje calculado y los parámetros de plegado, y realice una prueba con material de desecho para afinar los ajustes y garantizar los resultados deseados.
Siguiendo estos pasos, podrá determinar con precisión los ajustes adecuados para su plegadora, lo que le permitirá realizar operaciones de plegado de chapa precisas y eficaces.
Las fórmulas y los pasos previstos para calcular la fuerza de flexión son adecuados no sólo para la flexión angular de una chapa, sino también para la flexión en forma de arco (que técnicamente debería denominarse flexión angular con un radio de flexión grande).
Es crucial tener en cuenta que la formación de una forma de arco requiere un diseño de molde único.
Al proyectar el área de deformación, el cálculo debe basarse en los parámetros establecidos durante el proceso, que no pueden determinarse mediante una fórmula única.
En una fábrica específica de torres de hierro, curvamos con éxito un cilindro con un grosor de pared de 12 mm, un diámetro de 800 mm y una longitud de 16 m utilizando una prensa de 28000 kN. máquina de frenado y un molde circular.
El método descrito en este artículo se utilizó para determinar la fuerza de flexión y produjo resultados satisfactorios al diseñar un molde para una forma de arco.
Más información:
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
AR 
DE 
FR 
ID 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR