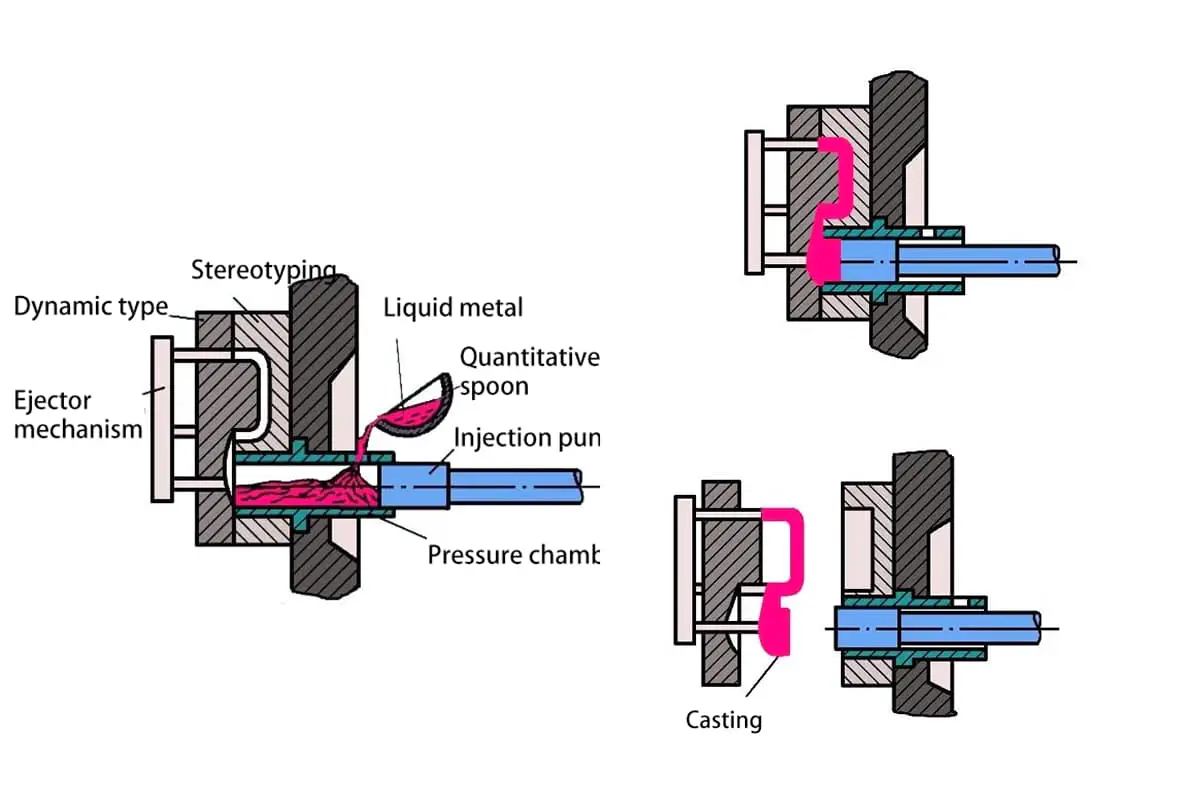
¿Qué hace que algunos componentes metálicos duren mientras otros fallan? La resistencia a la fatiga es clave, y en ella influyen factores como la concentración de tensiones, la calidad del material y las condiciones ambientales. Este artículo analiza estos elementos críticos y explica cómo influyen en la durabilidad y el rendimiento de las piezas mecánicas. Sumérjase para comprender la ciencia que hay detrás de la resistencia a la fatiga y aprenda ideas prácticas para mejorar la longevidad de sus componentes.
Normalmente, las curvas S-N obtenidas a partir de ensayos manuales se basan en los resultados de probetas estándar sin muescas. Sin embargo, las piezas reales utilizadas en aplicaciones del mundo real pueden tener formas, tamaños, condiciones de superficie, entornos de trabajo y características de carga diferentes, todo lo cual puede afectar significativamente a la resistencia a la fatiga de las piezas.
Los factores que afectan a la resistencia a la fatiga pueden agruparse en tres categorías: mecánica, metalurgia y medio ambiente. Estos factores son interdependientes, por lo que resulta difícil evaluar exhaustivamente su impacto en la resistencia a la fatiga. resistencia a la fatiga diseño y predicción de la vida a fatiga.
Los factores mecánicos están influidos principalmente por la concentración de tensiones y la tensión media. Los factores metalúrgicos están relacionados con la calidad del material, como su pureza y resistencia. Los factores medioambientales, por su parte, incluyen la presencia de sustancias corrosivas y las altas temperaturas.
En el caso de las piezas de vehículos ferroviarios, que en su mayoría funcionan en condiciones atmosféricas normales a temperaturas normales, la atención debe centrarse principalmente en los factores mecánicos y metalúrgicos, como la influencia de la forma y el tamaño de las muescas, el estado de la superficie y la tensión media.
La información específica sobre la influencia de estos factores en el límite de fatiga puede encontrarse en los manuales y materiales pertinentes mediante el uso de fórmulas empíricas.
El objetivo de este artículo es analizar las leyes y fenómenos importantes que deben comprenderse en el diseño de la resistencia a la fatiga y la predicción de la vida a fatiga, así como las precauciones que deben o deberían tenerse en cuenta.
Las piezas o componentes suelen tener muescas, como escalones, orificios para pernos, orificios para aceite, chaveteros, etc. La característica que define a estas muescas es que el área de la sección transversal de las piezas experimenta un cambio repentino en la muesca, lo que provoca un aumento significativo de la tensión en la raíz de la muesca. Este aumento de la tensión se denomina concentración de tensiones.
La concentración de tensiones en la muesca es el principal factor responsable de la reducción de la resistencia a la fatiga de los componentes. La concentración de tensiones hace que la tensión real en la raíz de la muesca sea mucho mayor que la tensión nominal, lo que conduce a la formación de grietas de fatiga y, finalmente, provoca el fallo o el daño de la pieza.
El grado de concentración de tensiones se describe mediante el factor de concentración de tensiones (también conocido como factor teórico de concentración de tensiones) Kt, que se expresa de la siguiente manera:
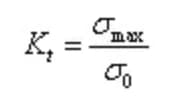
Aquí, σmax representa la tensión máxima, y σ0 representa la tensión media calculada dividiendo la carga por la sección transversal neta en la entalladura, también denominada tensión nominal.
Dentro de un cierto rango, cuanto menor sea el radio de curvatura ρ en la raíz de la muesca, mayor será la concentración de tensiones y mayor la reducción de la resistencia a la fatiga. Sin embargo, en el caso de materiales plásticos como el acero de bajo y medio carbono, a medida que el radio de curvatura en la raíz de la entalla se hace más pequeño y se aproxima a unos pocos milímetros, la reducción de la resistencia a la fatiga se hace menor o incluso deja de reducirse.
En este caso, el factor de concentración de tensiones ya no es un reflejo exacto del impacto de la entalla en la resistencia a la fatiga. Para reflejar con mayor exactitud la verdadera reducción de la resistencia a la fatiga, el factor de entalla por fatiga Kf (anteriormente conocido como factor de concentración efectiva de tensiones).
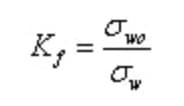
Aquí, σw0 y σw representan los límites de fatiga de las probetas lisas sin muescas y de las probetas con muescas, respectivamente.
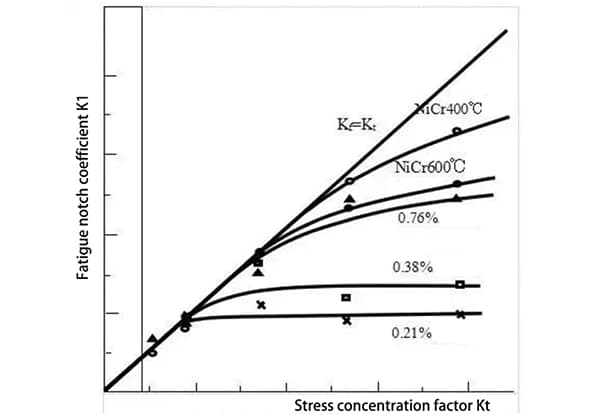
La siguiente figura ilustra la relación entre el factor de concentración de esfuerzos Kt y el factor de entalla por fatiga Kf para el acero.
Como se muestra en la figura, para el acero de bajo y medio carbono, cuando el factor de concentración de tensiones es inferior a 2 o 2,5, Kt y Kf suelen ser similares. Sin embargo, cuando se supera este valor, el aumento de Kf se ralentiza considerablemente.
Para los aceros con alto contenido en carbono y una elevada relación de resistencia, Kf aumenta linealmente con Kt a gran distancia.
Puede concluirse que la resistencia a la fatiga del acero de alta resistencia es muy sensible a la presencia de muescas, mientras que la resistencia a la fatiga del acero de resistencia baja y media es menos sensible a las muescas.
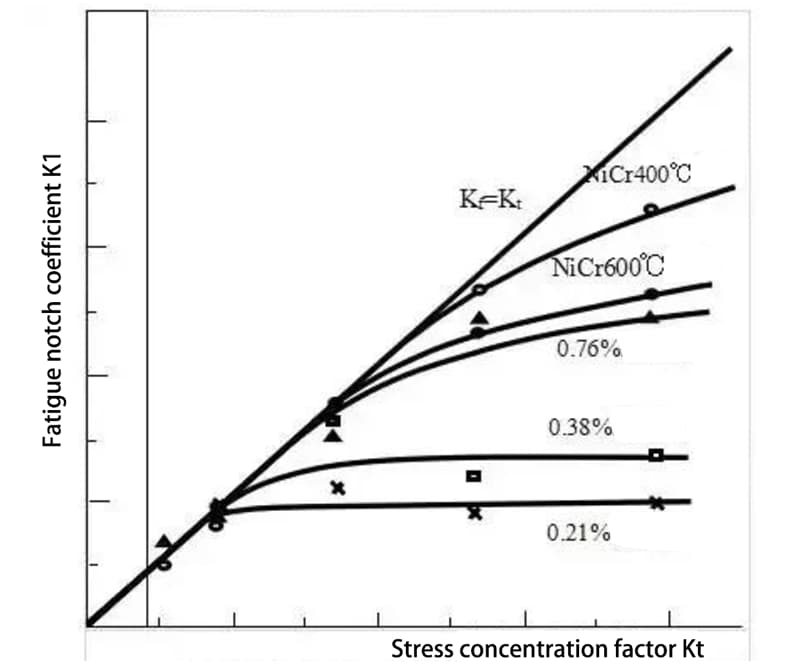
En general, Kf es inferior a Ktpero en el caso de muescas afiladas en acero con alto contenido en carbono, Kt puede ser mayor que Kf. Esto también puede ocurrir en las piezas atornilladas, donde Kt puede llegar a 4 y Kf puede ser de 8 a 10. Esto se debe a la distribución desigual de la carga entre los hilos, con varias cargas concentradas en un hilo.
Para los materiales lisos, los tratamientos térmicos superficiales como el temple superficial, la carburación y la nitruración pueden mejorar eficazmente su resistencia a la fatiga. Sin embargo, estos métodos pueden resultar ineficaces o incluso reducir la resistencia a la fatiga de los materiales entallados. Esto se debe a que la resistencia superficial se mejora mediante el tratamiento térmico, pero también aumenta la sensibilidad a las muescas.
La siguiente figura ilustra el cambio en la resistencia a la fatiga del acero de alta resistencia entallado y del acero de baja resistencia con buena plasticidad a medida que aumenta la concentración de tensiones. En el rango de menor concentración de tensiones KtLa resistencia a la fatiga del acero de alta resistencia es significativamente mayor que la del acero de baja resistencia. Sin embargo, a medida que aumenta el factor de concentración de tensiones, la resistencia a la fatiga del acero de alta resistencia disminuye más rápidamente que la del acero de baja resistencia, lo que hace que la resistencia a la fatiga del acero de alta resistencia sea casi igual a la del acero de baja resistencia.
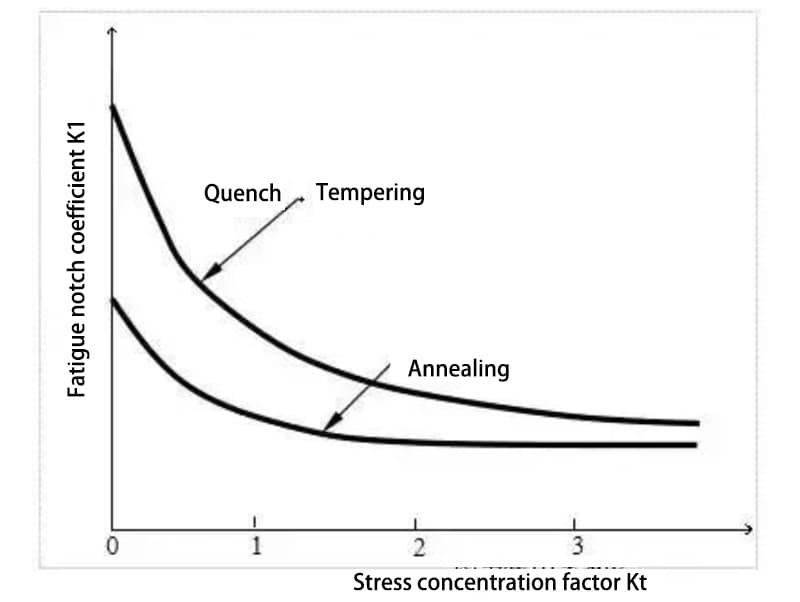
En el caso de los componentes soldados, la resistencia a la fatiga suele reducirse considerablemente debido a la combinación del zona afectada por el calor estar situado cerca de la muesca estructural y la presencia de defectos de soldadura y tensiones de tracción residuales. Esta reducción puede ser varias veces superior a la normal o incluso más de diez veces.
El coeficiente de entalla por fatiga también puede verse afectado por el tamaño de las piezas. Por regla general, para una misma entalla, el coeficiente de entalla por fatiga aumenta al aumentar el tamaño.
Para mejorar la vida a fatiga de los materiales o componentes con muescas, lo más eficaz es realizar un diseño estructural y una selección de procesos que reduzcan o mejoren la concentración de tensiones.
Sin embargo, una superficie rugosa y un gran tamaño pueden reducir la resistencia a la fatiga de los componentes.
El diámetro de la probeta utilizada para los ensayos de fatiga suele oscilar entre 5 y 10 mm, que es mucho menor que el tamaño real de las piezas.
Para los componentes sometidos a cargas de flexión y torsión, la resistencia a la fatiga disminuye a medida que aumenta el tamaño. Sin embargo, para las cargas axiales de tracción y compresión, el tamaño tiene un efecto mínimo.
La influencia del tamaño en el límite de fatiga se representa mediante el coeficiente de influencia del tamaño (ε).
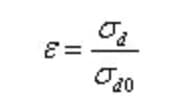
Aquí, σd y σd0 representan los límites de fatiga de probetas lisas de cualquier tamaño y del tamaño estándar, respectivamente.
El efecto del tamaño en acero de alta resistencia es mayor que el del acero de baja resistencia, y el efecto del tamaño es más pronunciado en las piezas con superficies rugosas.
El efecto del tamaño se debe principalmente al impacto del estado de la estructura del material y el gradiente de tensión en la resistencia a la fatiga de los componentes más grandes.
A medida que aumenta el tamaño del material, resulta más difícil controlar el proceso de fabricación, y la estructura del material se vuelve menos uniforme y compacta, con más defectos metalúrgicos y una mayor superficie que aumenta la probabilidad de estos defectos.
El resultado es un mayor riesgo de fatiga y grietas en la superficie de las probetas de gran tamaño. La concentración local de tensiones provocada por defectos metalúrgicos conduce a la formación de grietas de fatiga.
En cuanto a la influencia del gradiente de tensión, cuando se somete a flexión, torsión y otras cargas, cuanto mayor es el tamaño del componente, menor es el gradiente de tensión de trabajo, mayor es la tensión media por unidad de superficie y más fácil es que se formen grietas por fatiga.
Las condiciones de la superficie afectan a varios factores, como rugosidad superficialestado de tensión superficial, grado de deformación plástica superficial, defectos superficiales y otros.
En el proceso de ensayo, se utiliza la muestra estándar con superficie pulida; sin embargo, las piezas reales suelen tener superficies mecanizadas, forjadas o fundidas.
El mecanizado puede provocar el endurecimiento por deformación del plástico en la superficie de la pieza.
El corte suele dejar tensiones residuales de compresión en la superficie, lo que mejora la resistencia a la fatiga, pero sólo hasta cierto punto.
El rectificado, por el contrario, puede provocar tensiones residuales de tracción, perjudiciales para la resistencia a la fatiga.
Además, la rugosidad a microescala de las superficies mecanizadas puede provocar la concentración de tensiones y disminuir la resistencia a la fatiga.
El efecto combinado de estos factores da como resultado una menor resistencia a la fatiga en comparación con la muestra estándar.
Las superficies forjadas o fundidas suelen presentar una mayor rugosidad y capas superficiales de endurecimiento por deformación, así como tensiones residuales de compresión, lo que provoca una disminución significativa de la resistencia a la fatiga.
En conclusión, cuanto más rugoso es el método de tratamiento de la superficie, mayor es su impacto en la reducción de la resistencia a la fatiga.
El efecto de las condiciones de procesado superficial sobre la resistencia a la fatiga se representa mediante el coeficiente de procesado superficial (β).
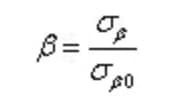
Aquí, σβ representa el límite de fatiga de una muestra lisa estándar en un determinado estado de la superficie, σβ0 representa el límite de fatiga de una muestra lisa estándar pulida, y "en el extranjero" se refiere a la muestra lisa estándar con superficie pulida.
Desde una perspectiva metalúrgica, el mecanizado en bruto tiene un impacto significativo en la resistencia a la fatiga de los materiales de alta resistencia, por lo que es posible que el acero de alta resistencia no mejore la resistencia a la fatiga en estados de mecanizado en bruto. Esto se debe principalmente a la alta sensibilidad de los materiales de alta resistencia a las superficies rugosas y al mínimo efecto de endurecimiento por deformación del mecanizado en la superficie del acero de alta resistencia.
Se ha investigado poco sobre el impacto de los defectos superficiales, como la descarburizaciónLa resistencia a la fatiga no se ve afectada por los defectos superficiales, las marcas de golpes en la superficie y los arañazos. Sin embargo, los defectos superficiales causados por razones accidentales pueden tener un impacto significativo en la resistencia a la fatiga. Por lo tanto, debe prestarse suficiente atención a estas cuestiones en el diseño y, especialmente, en el proceso de fabricación.
Para los materiales lisos, el tratamiento térmico superficial y otros métodos de modificación de la superficie pueden mejorar la resistencia a la fatiga. Sin embargo, para materiales con muescas, como las piezas reales, estos métodos tienen poco efecto e incluso pueden tener un efecto adverso. En consecuencia, el granallado granallado y el laminado se utilizan a menudo para generar endurecimiento por deformación y tensión de compresión residual en la superficie, mejorando así la resistencia a la fatiga de los componentes.
Sin embargo, estos dos métodos no suelen mejorar significativamente la resistencia a la fatiga de las piezas con agujeros. Las últimas investigaciones demuestran que el uso de un simple troquel metálico achaflanar una pequeña parte del borde del orificio puede mejorar significativamente la resistencia a la fatiga e incluso eliminar el impacto de la muesca, reduciendo el límite de fatiga.
En el pasado, se creía comúnmente que la razón principal de la mejora de la resistencia a la fatiga de los métodos de transformación plástica superficial se debía a que la tensión residual de compresión generada en la superficie compensaba parte de la tensión de trabajo.
Sin embargo, la tensión concentrada de compresión producida por la tensión residual de compresión en la muesca compensa el efecto adverso de la muesca. La deformación plástica refuerza las zonas débiles cercanas a la entalladura, haciendo que la estructura sea más uniforme y mejorando la resistencia general, lo que a su vez mejora el nivel de tensión que produce las grietas de fatiga.
Además, la tensión residual de compresión hace que las grietas de fatiga dejen de crecer y se conviertan en grietas de permanencia.
Como ya se ha dicho, la principal causa de fallo por fatiga es la tensión dinámica, pero el componente de tensión estática, o tensión media, también tiene cierto impacto en el límite de fatiga. En un rango específico de tensión estática, un aumento de la tensión estática de compresión aumentará el límite de fatiga, mientras que un aumento de la tensión estática de tracción lo reducirá.
Está ampliamente aceptado que tensión residual tiene un efecto sobre el límite de fatiga similar al de la tensión media. Para un material determinado, se puede trazar un diagrama de límite de fatiga basado en sus resultados de límite de fatiga bajo tensiones medias variables o relaciones de tensiones (R).
El diagrama siguiente presenta una magnitud adimensional, la relación entre la tensión media (σm) o tensión residualhasta el límite de resistencia (σb), en el eje x, y la relación entre la amplitud de la tensión (σa) hasta el límite de fatiga cíclica simétrica (σ-1), en el eje y.

La figura muestra que la mayoría de los puntos de datos de las pruebas se sitúan entre líneas rectas y curvas. La línea recta se denomina línea de Goodman, mientras que la curva se conoce como parábola de Gerber. La línea de Soderberg se obtiene sustituyendo el límite de resistencia (σb) con el límite elástico (σs). Del mismo modo, la línea de Morrow se obtiene sustituyendo σb por la tensión de fractura real (σf).
Línea Goodman:
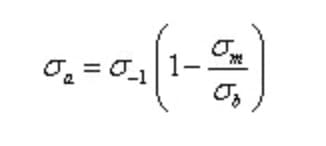
Línea Gerber:

Línea Soderberg:

Línea Morrow:

La línea de Goodman es un enfoque conservador y sencillo para los metales dúctiles, por lo que es un método muy utilizado en el diseño de fatiga. Otro método de uso frecuente es el diagrama de Goodman ideal mejorado.
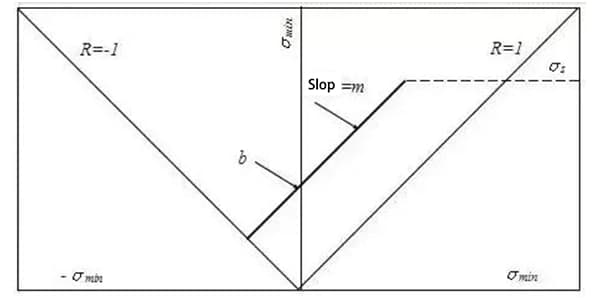
La siguiente figura ilustra el Diagrama de Goodman Ideal Mejorado de una viga de acero a tope en forma de I sometida a una carga de fatiga por flexión. El eje x representa la tensión mínima (σmin), el eje y representa la tensión máxima (σmax), y la ecuación lineal es la siguiente:

Donde, m es la pendiente de la línea de Goodman, b es la intercepción de la línea en el eje y, y es el límite de fatiga del ciclo de pulsación cuando la tensión mínima es igual a cero.
Cuando el límite de fatiga se expresa mediante la tensión máxima, es decir, σ w= σ Maxconsiderando la relación de tensiones R= σ max/ σ Min.
La línea Morrow incluye:

El límite de fatiga a una determinada relación de esfuerzos (R) puede calcularse mediante la fórmula anterior. Sin embargo, la estructura real de un vehículo es mucho más compleja que las condiciones de ensayo en las que se obtuvo la curva S-N, como el tipo de soldadura y las concentraciones de tensión.
La norma americana AAR proporciona valiosas directrices para la resistencia a la fatiga de diversas estructuras de soldadura y, por lo tanto, los valores de "b" y "m" en los cálculos reales se toman de la norma AAR.
Los resultados de las pruebas indican que el impacto de los componentes de la carga estática sobre el coeficiente de concentración de tensiones, el coeficiente de dimensión y el coeficiente de superficie es menor y puede despreciarse.