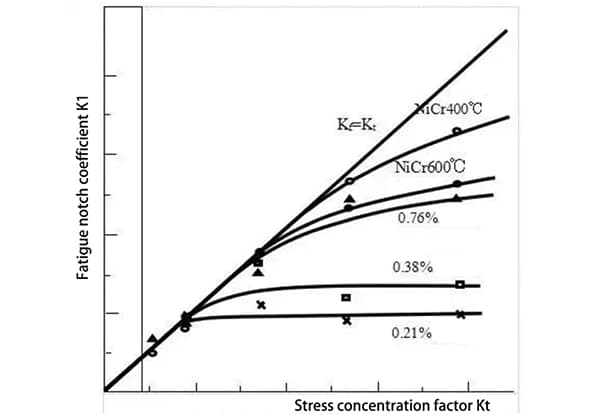
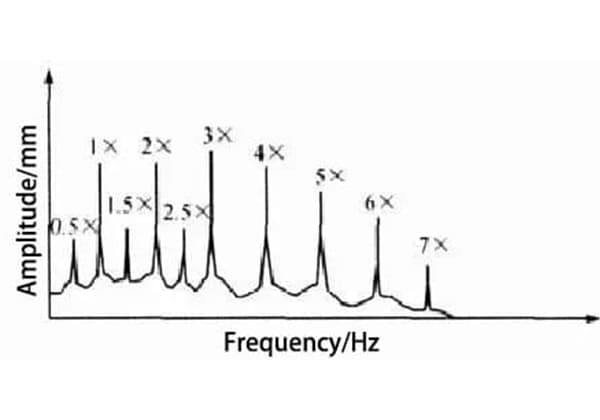
¿Cómo pueden predecir los ingenieros cuándo fallará un material sometido a esfuerzos repetidos? Este artículo presenta la curva S-N, una herramienta clave en el análisis de fatiga. Aprenderá cómo se tratan la tensión media, la conversión de la tensión multiaxial y la tensión irregular para predecir la vida a fatiga del material. Comprender estos conceptos puede ayudar a diseñar componentes más duraderos y fiables. Siga leyendo para explorar las complejidades del análisis de fatiga y garantizar la longevidad de sus proyectos de ingeniería.
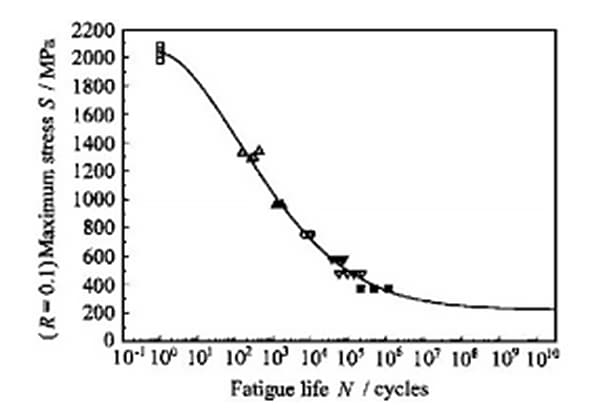
Las propiedades de fatiga de los materiales suelen expresarse mediante ciclos de tensión uniaxial, conocidos como curvas S-N. Es importante señalar que en este contexto no se está considerando la teoría de la fatiga basada en la mecánica de la fractura.
La variación de la tensión a lo largo del tiempo suele seguir un patrón regular, como una onda sinusoidal, una onda cuadrada o un impulso. Sin embargo, a menudo no se tiene en cuenta la influencia de la tensión media en el comportamiento a la fatiga (es decir, el impacto de r=Smin/Smax ≠ -1).
En la realidad, el estado de tensión suele ser multiaxial, con una variación de tensión irregular y r≠-1. La correspondencia entre la tensión real y el comportamiento a fatiga medido en el laboratorio, que implica una variación regular de la tensión, una tensión uniaxial y r=1, constituye la base del análisis de fatiga.
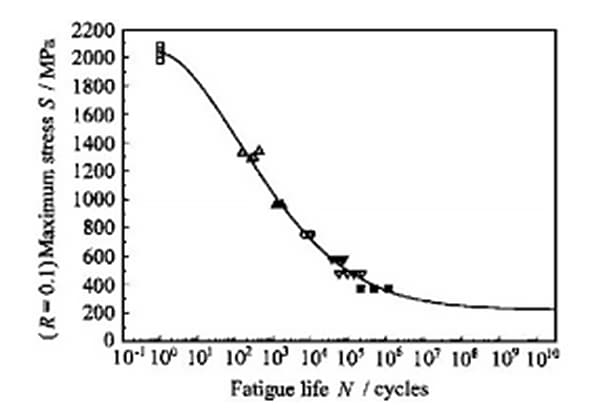
Cuando se dispone de curvas S-N para diferentes valores de r, se suele emplear el método de interpolación para determinar la curva S-N para valores desconocidos de r.
En los casos en los que sólo se disponga de una curva S-N con r=-1, se puede utilizar la siguiente fórmula para calcular la tensión equivalente. Esta fórmula convierte la tensión uniaxial de r≠-1 en la tensión uniaxial cuando r=-1, que se conoce como tensión equivalente:
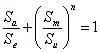
Donde, Sa es la amplitud de media tensión, Se es la tensión equivalente deseada, Sm es la tensión media, y diferentes valores de Su y n constituyen teorías diferentes:
Las siguientes opciones de tensión están disponibles para determinar el tipo de tensión utilizada para la transformación: Tensión equivalente de Von Mises, tensión de cizalladura máxima, tensión principal máxima o un componente de tensión específico (como Sx, Syz, etc.).
A veces, también se emplea la tensión de Mises con signo, permaneciendo invariable su magnitud. El signo corresponde al signo de la tensión principal máxima. Una ventaja de este método es que permite considerar los efectos de tensión o compresión, que se reflejan en la tensión media o r.
Similar a la teoría de la fuerzaLa conversión de la tensión equivalente de Von Mises y la tensión máxima de cizalladura son adecuadas para materiales con una gran ductilidad, mientras que la conversión de la tensión principal máxima es apropiada para materiales quebradizos.
La curva de tiempo de tensión uniaxial equivalente de alta y baja irregular se analiza para extraer una serie de ciclos de tensión simples (Sa, Sm) y sus tiempos correspondientes.
El recuento y las estadísticas pueden realizarse mediante varios métodos, como el método dependiente de la trayectoria y el método independiente de la trayectoria.
Para completar el proceso de recuento se aplica el método de correlación de trayectorias, que es el método de recuento del flujo de lluvia más utilizado. Su algoritmo y principio se explican en "Downing, S., Society, D. (1982) Simplified rain flow counting algorithms. Int J Fatigue, 4, 31 - 40".
Tras el tratamiento del flujo de lluvia, la curva temporal de tensiones irregulares se transforma en una serie de ciclos simples (Sa, Smy nidonde ni es el número de ciclos).
Este método permite calcular y analizar la teoría de acumulación de daños (criterio de Miner): Suma (ni/Ni), donde Ni es la vida correspondiente al ciclo de tensión (considerando Sa, Sm(véase más arriba).
Esta técnica se utiliza habitualmente para medir el factor de seguridad tras un determinado número de ciclos o la vida útil correspondiente a un ciclo de tensión complejo específico.
En la actualidad, los programas informáticos comerciales de análisis de la fatiga se basan principalmente en el proceso mencionado.
Sin embargo, hay que señalar que el análisis de la fatiga es un análisis empírico, y actualmente no existe una teoría madura y completa.
Existen diversas perspectivas sobre la conversión de la tensión multiaxial en tensión uniaxial.
La tensión de Von Mises, por ejemplo, es una magnitud de dimensión de tensión basada en la idea de la energía específica de cambio de forma.
Utilizar los conceptos de positivo y negativo o tensión y compresión es un método impreciso, y no se recomienda.
La selección del tipo de tensión a adoptar depende de la posible tendencia de las grietas en los materiales o estructuras para determinar qué tipo de tensión es el principal factor de control. fallo por fatiga.
La práctica de la ingeniería ha demostrado que el acero con buena plasticidad se daña a menudo debido a la carga dinámica repetida de la tensión principal en casos de fallo por fatiga.
Suplemento sobre el tratamiento del efecto del estrés medio:
"Si existen curvas S-N bajo diferentes valores de R, generalmente se utiliza el método de interpolación para determinar la curva S-N bajo valores desconocidos de R".
Éste es sólo un método, que resulta útil cuando hay varias tensiones que comprobar. Sin embargo, este método puede ser engorroso cuando se comprueba una sola vida de tensión.
Otro método consiste en determinar la semiamplitud de tensión equivalente en la condición de R = -1 y, a continuación, aplicar directamente la curva S-N.
Cuando existe una tensión media, la curva S-N no puede utilizarse directamente. En su lugar, utilice la CURVA DE GOODMAN o la CURVA DE GOODMAN modificada.
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
AR 
DE 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO