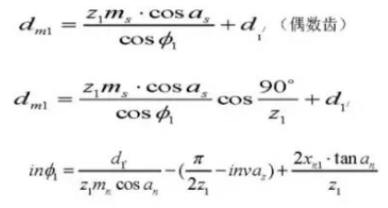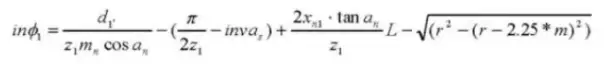¿Alguna vez se ha preguntado por el fascinante mundo de los engranajes? En esta entrada del blog, exploraremos la historia, los tipos y la terminología de estos componentes mecánicos esenciales. Acompáñenos mientras nos adentramos en los entresijos de los engranajes, guiados por la experiencia de un avezado ingeniero mecánico. Descubra cómo han evolucionado los engranajes a lo largo de los siglos y conozca su papel crucial en la maquinaria moderna.
Un engranaje es un componente mecánico dentado de precisión diseñado para engranar con otros engranajes o componentes dentados. Es un elemento fundamental en los sistemas de transmisión de potencia, ya que convierte la velocidad de rotación y el par entre ejes. Los engranajes se caracterizan por su forma circular con dientes espaciados uniformemente a lo largo de la periferia, que suelen seguir un perfil evolvente para un engrane óptimo.
La aplicación de los engranajes en la transmisión mecánica y en todo el campo más amplio de la ingeniería mecánica es excepcionalmente diversa y crucial. Forman parte integral de una amplia gama de maquinaria y dispositivos, desde simples herramientas manuales hasta complejos equipos industriales y vehículos de alto rendimiento. Los engranajes permiten un control preciso de la velocidad, la dirección y la fuerza en sistemas mecánicos, lo que los hace indispensables en trenes de potencia, reductores, diferenciales y otros innumerables conjuntos mecánicos.
La versatilidad de los engranajes se debe a su capacidad para fabricarse en diversos tamaños, materiales y configuraciones, como engranajes rectos, helicoidales, cónicos y helicoidales, cada uno de ellos adaptado a aplicaciones y requisitos de rendimiento específicos. A medida que avanza la tecnología, el diseño y la fabricación de engranajes siguen evolucionando, incorporando nuevos materiales, técnicas de producción y métodos de optimización para mejorar la eficacia, la durabilidad y la reducción del ruido en los sistemas mecánicos.
Ya en el año 350 a.C., el célebre filósofo griego Aristóteles escribió sobre los engranajes.
Alrededor del año 250 a.C., el matemático Arquímedes también describió en su literatura el uso de la turbina y el tornillo sin fin en un polipasto.
En el reloj de agua de Ktesibios, en Irak, aún se conservan engranajes de siglos anteriores a Cristo.

La historia de los engranajes en China se remonta a la Antigüedad y tiene una larga y extensa trayectoria. Según los registros históricos, los engranajes ya se utilizaban en la antigua China entre los años 400 y 200 a. C.
Los engranajes de bronce excavados en la provincia de Shanxi son los más antiguos descubiertos hasta ahora en el mundo. Los carros de guiado que reflejaban los logros de la ciencia y la tecnología antiguas eran artefactos mecánicos que giraban en torno a mecanismos de engranaje.
Durante el Renacimiento italiano, en la segunda mitad del siglo XV, el famoso genio polifacético Leonardo da Vinci no sólo dejó una huella indeleble en los aspectos culturales y artísticos, sino que también realizó importantes aportaciones a la historia de la tecnología de los engranajes.
Después de más de 500 años, los engranajes actuales conservan los bocetos de los prototipos de entonces.
(1) Engranaje recto
(2) Cremallera
(3) Engranaje helicoidal con ejes cruzados

(4) Engranaje cónico
(5) Engranaje cónico hipoide de alta relación de transmisión
(6) Engranaje helicoidal
No fue hasta finales del siglo XVII cuando se empezó a estudiar la forma de los dientes de la rueda, que podía transmitir el movimiento con precisión. Tras la Revolución Industrial del siglo XVIII en Europa, la aplicación de la transmisión por engranajes se generalizó.
Primero se desarrolló el engranaje cicloidal, seguido del engranaje evolvente. A principios del siglo XX, la rueda evolvente dominaba su aplicación. Más tarde se desarrollaron engranajes como el helicoidal, el de arco, el cónico y el oblicuo.
Hoy en día, la moderna tecnología de engranajes ha realizado grandes avances. Los módulos de engranaje oscilan entre 0,004 y 100 milímetros, y el diámetro del engranaje puede variar entre 1 milímetro y 150 metros. En transmisión de energía puede alcanzar los 100.000 kilovatios, y la velocidad de rotación puede llegar a las 100.000 revoluciones por minuto. La velocidad circunferencial máxima puede alcanzar los 300 metros por segundo.
A escala internacional, los dispositivos de engranajes de transmisión de potencia evolucionan hacia la miniaturización, la alta velocidad y la normalización. Algunas tendencias en el diseño de engranajes incluyen la aplicación de engranajes especiales, el desarrollo de dispositivos de engranajes planetarios y la investigación y el desarrollo de sistemas de engranajes de baja vibración y ruido.
Existen varios tipos de engranajes, y el método más común de clasificación se basa en el eje del engranaje.
En general, los engranajes se clasifican en tres tipos: de eje paralelo, de eje de intersección y de eje oblicuo.
Engranajes de ejes paralelos: incluidos engranajes rectos, engranajes helicoidales, engranajes internos, cremalleras y cremalleras helicoidales.
Iengranajes de eje transversal: incluidos engranajes cónicos rectos, engranajes cónicos en espiral, engranajes cónicos de grado cero, etc.
Engranajes de eje oblicuo: incluidos engranajes helicoidales con ejes cruzados, engranajes helicoidales, engranajes cónicos hipoides, etc.
| Tipo de transmisión | Tipo de engranaje | Eficacia de transmisión (%) | Representación gráfica en 3D |
Eje paralelo | Engranajes rectos | 98.0-99.5 |  |
| Engranajes helicoidales |  | ||
| Cremalleras,Cremalleras helicoidales |  | ||
| Engranajes Intemal | 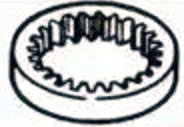 | ||
Eje de intersección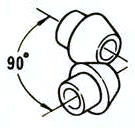 | Engranajes de inglete | 98.0-99.0 |  |
| Engranajes cónicos rectos |  | ||
| Engranajes cónicos en espiral |  | ||
Eje oblicuo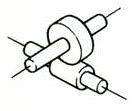 | Engranajes de tornillo | 70.0-95.0 |  |
| Gusanos | 30.0-90.0 |  | |
| Ruedas helicoidales | 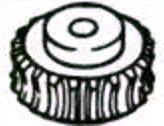 |
El rendimiento indicado en la tabla anterior es el rendimiento de transmisión, que no incluye las pérdidas por rodamientos y lubricación por agitación. El engrane de los pares de engranajes de ejes paralelos y de ejes transversales es básicamente de rodadura, y el deslizamiento relativo es muy pequeño, por lo que la eficiencia es alta.
El engrane de pares de engranajes de eje escalonado, como los engranajes helicoidales y los engranajes helicoidales, tiene un impacto significativo de fricción porque consiguen la transmisión de potencia mediante deslizamiento relativo, lo que provoca una reducción de la eficacia de la transmisión en comparación con otros engranajes.
La eficiencia de los engranajes se refiere a la eficiencia de transmisión de los engranajes en su estado normal de montaje.
Si hay una instalación incorrecta, especialmente cuando la distancia de montaje del engranaje cónico es incorrecta y causa un error en la intersección del mismo engranaje cónico, su eficiencia disminuirá significativamente.
1. Engranajes rectos
Engranajes cilíndricos cuyas líneas de dientes y líneas axiales son paralelas. Se utilizan mucho en la transmisión de potencia porque son fáciles de procesar.
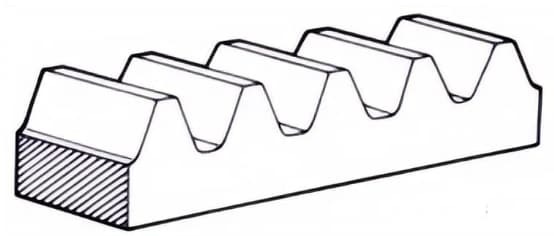
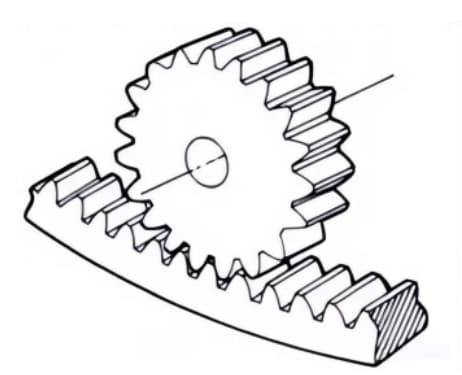
2. Estante
Engranaje de dientes rectos que engrana con engranajes rectos. Puede considerarse un caso especial en el que el diámetro de paso del engranaje recto es infinitamente grande.
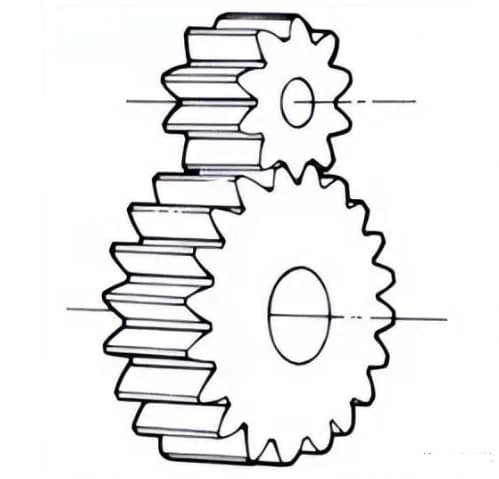
3. Engranajes internos
Engranajes con dientes mecanizados en el interior de un anillo que engranan con engranajes rectos. Se utilizan principalmente en aplicaciones como mecanismos de transmisión por engranajes planetarios y acoplamientos de engranajes.
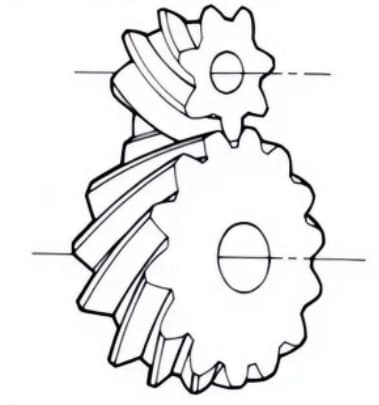
4. Engranajes helicoidales
Engranajes cilíndricos con líneas de dientes en forma de hélice. Se utilizan mucho por su gran resistencia y suavidad de funcionamiento, en comparación con los engranajes rectos. Generan empuje axial durante la transmisión.
5. Cremallera helicoidal
Engranaje de cremallera que engrana con engranajes helicoidales. Equivale al caso en el que el diámetro de paso del engranaje helicoidal se hace infinitamente grande.
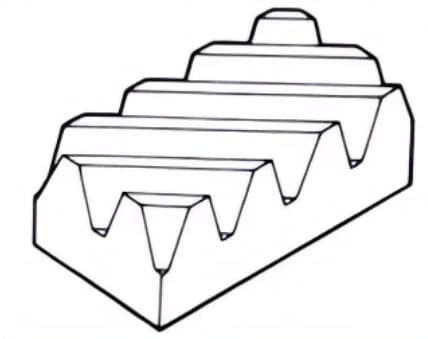
6. Engranajes en espiga
Engranajes formados por dos ruedas helicoidales con ángulos de hélice opuestos. Tienen la ventaja de no generar empuje axial.
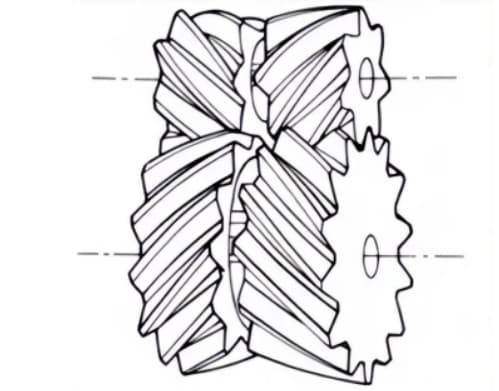
1. Engranajes cónicos rectos
Ruedas cónicas con líneas de dientes paralelas a la generatriz del cono. Son relativamente fáciles de fabricar en comparación con otros tipos de ruedas cónicas.
Por lo tanto, se utilizan ampliamente en aplicaciones de engranajes cónicos para la transmisión de potencia.
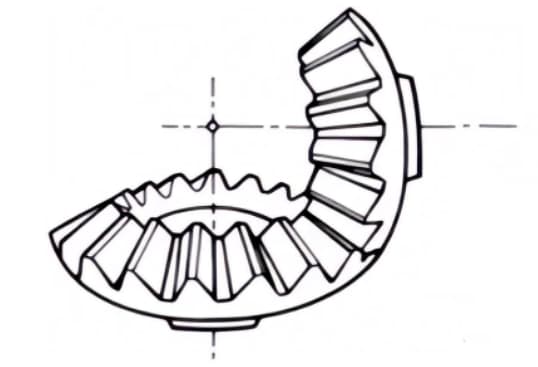
2. Engranajes cónicos en espiral
Engranajes cónicos con líneas de dientes curvadas y un ángulo de hélice. Aunque son más difíciles de fabricar que los engranajes cónicos rectos, se utilizan mucho como engranajes de alta resistencia y bajo nivel de ruido.
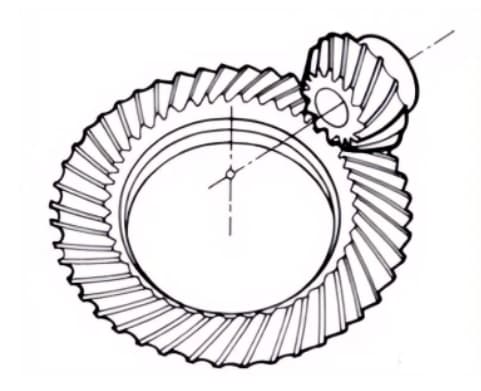
3. Engranajes cónicos cero
Ruedas cónicas curvas con un ángulo de hélice de cero grados. Presentan las características de las ruedas cónicas rectas y helicoidales, con la superficie del diente sometida a la misma situación de fuerza que las ruedas cónicas rectas.
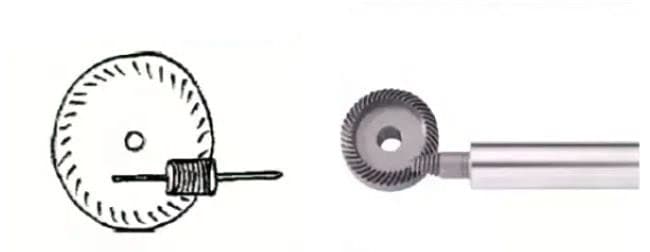
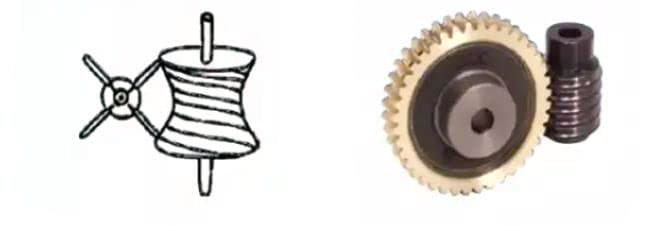
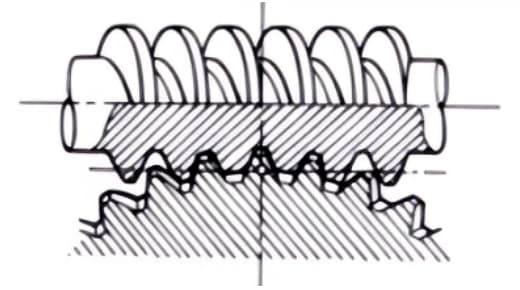
1. Par de tornillo sin fin
El término "par de tornillo sin fin" se refiere a la combinación de un tornillo sin fin y una rueda helicoidal que engrana con él. La mayor característica del par de ruedas helicoidales es que se puede obtener una gran relación de transmisión con un solo par, y funcionan de forma silenciosa. Sin embargo, su bajo rendimiento es una desventaja.
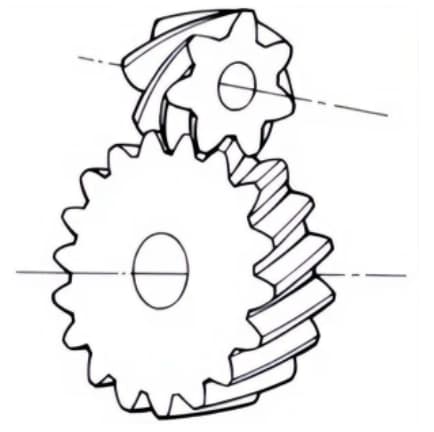
2. Par de engranajes cilíndricos y de tornillo sin fin
Término utilizado cuando se utilizan pares de engranajes helicoidales cilíndricos para la transmisión entre ejes escalonados. Pueden utilizarse en el caso de pares de engranajes helicoidales o entre pares de engranajes helicoidales y rectos. Aunque funcionan con suavidad, sólo son adecuados para su uso con cargas ligeras.
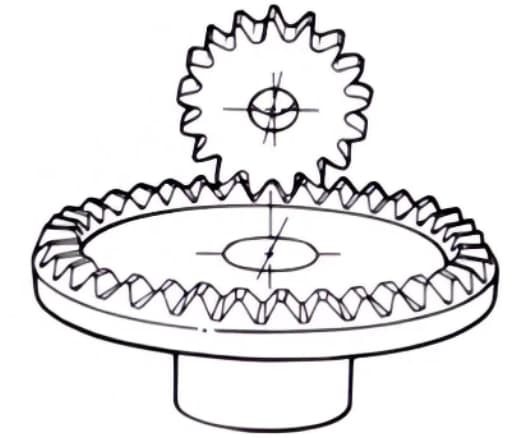
1. Engranajes frontales
Engranajes en forma de disco que pueden engranar con engranajes rectos o engranajes helicoidales. Se utilizan para la transmisión entre ejes ortogonales y ejes escalonados.
2. Par de engranajes de tornillo sinfín de reloj de arena
El término "par de ruedas helicoidales de reloj de arena" hace referencia a la combinación de un tornillo sin fin de reloj de arena y una rueda helicoidal que engrana con él. Aunque son más difíciles de fabricar que los pares de ruedas helicoidales cilíndricas, pueden transmitir cargas pesadas.
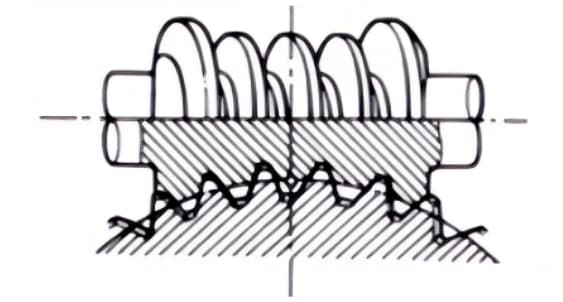
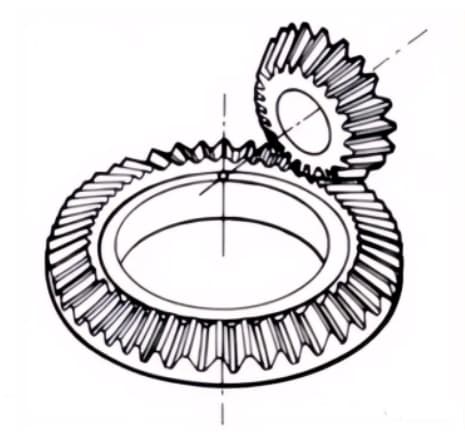
3. Engranajes hipoides
Engranajes cónicos utilizados para la transmisión entre ejes escalonados. Los engranajes mayor y menor se mecanizan excéntricamente, de forma similar al caso de los engranajes cónicos en espiral. El principio de engrane es muy complejo.
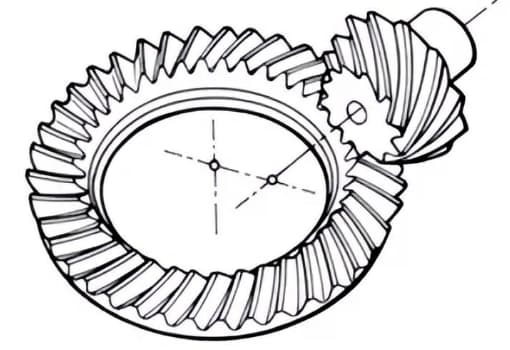
Los engranajes tienen una terminología y unos métodos de presentación distintivos. Con el fin de mejorar la comprensión de los engranajes, he aquí algunos términos básicos de uso común.
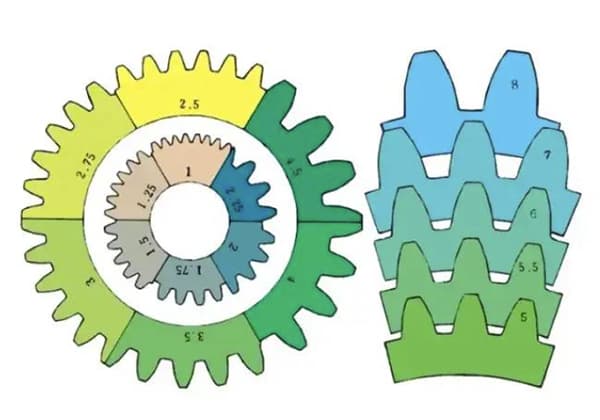
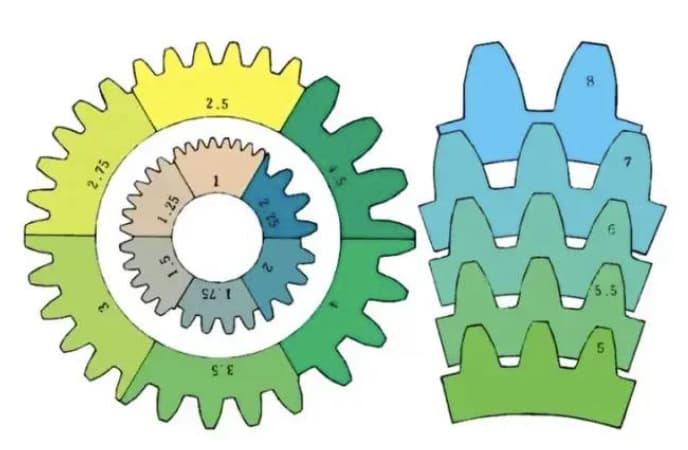
m1, m3, m8... se conocen como módulo 1, módulo 3, módulo 8 respectivamente. El módulo se utiliza universalmente en todo el mundo para indicar el tamaño del engranaje, utilizando el símbolo m (módulo) y números (milímetros) para representar el tamaño de los dientes.
Cuanto mayor sea el número, mayor será la marcha.
En los países que utilizan unidades imperiales, como Estados Unidos, el tamaño de los dientes se indica mediante el símbolo DP (paso diametral) y números (el número de dientes de una rueda dentada con un diámetro de paso de 1 pulgada).
Por ejemplo: DP24, DP8, etc. También existe una comparación y un método especial para indicar el tamaño de los dientes mediante el símbolo CP (paso circular) y números (milímetros), como CP5, CP10.
El paso (p) se obtiene multiplicando el módulo por pi. El paso es la longitud entre dientes adyacentes.
La fórmula es: p= pi x m
Comparación del tamaño de los dientes de distintos módulos:
El ángulo de presión es un parámetro que determina la forma de los dientes del engranaje. Se refiere a la inclinación de la superficie de los dientes del engranaje y suele fijarse en 20 grados (α).
Antes eran habituales las marchas con un ángulo de presión de 14,5 grados.
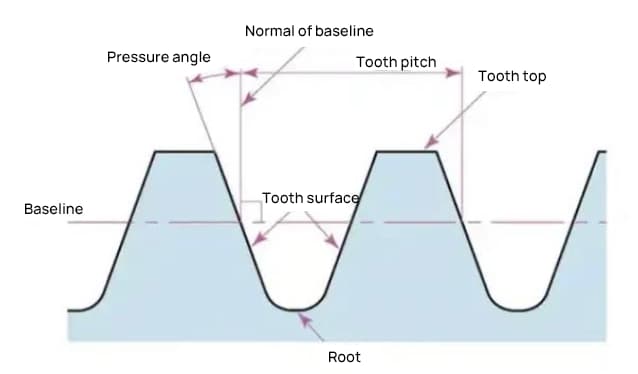
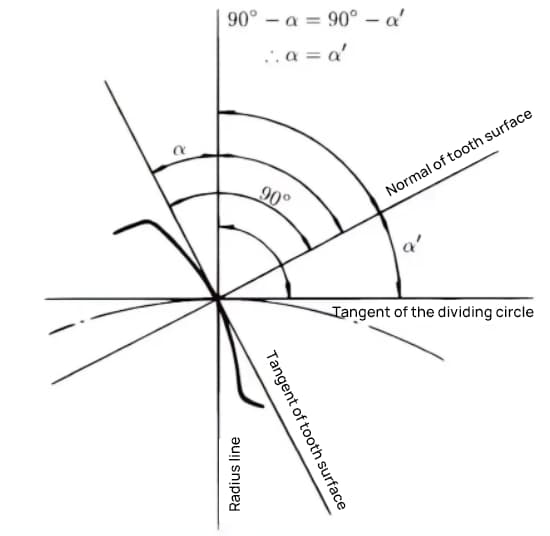
El ángulo de presión es el ángulo formado entre el radio y la tangente del perfil del diente en un punto determinado de la superficie del diente (generalmente el nodo). Como se muestra en la imagen, α es el ángulo de presión. α' también es un ángulo de presión, ya que α' = α.
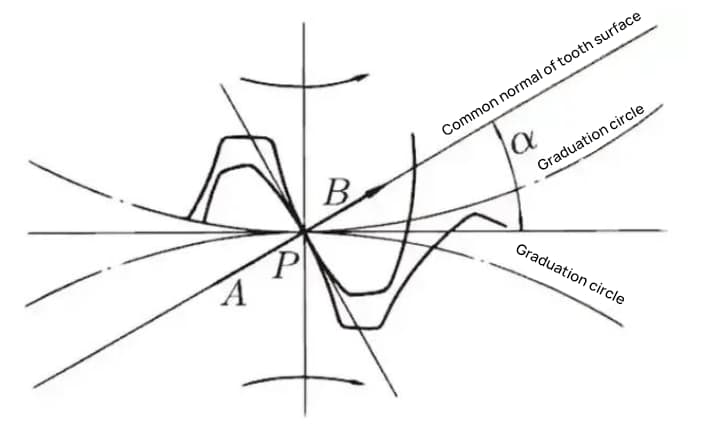
Cuando el estado de engrane del Engranaje A y el Engranaje B se ve desde el nodo, el Engranaje A empuja al Engranaje B desde el nodo. En este momento, la fuerza motriz actúa sobre la normal común del Engranaje A y el Engranaje B. En otras palabras, la normal común es la dirección de la fuerza y la dirección del cojinete de presión, siendo α el ángulo de presión.
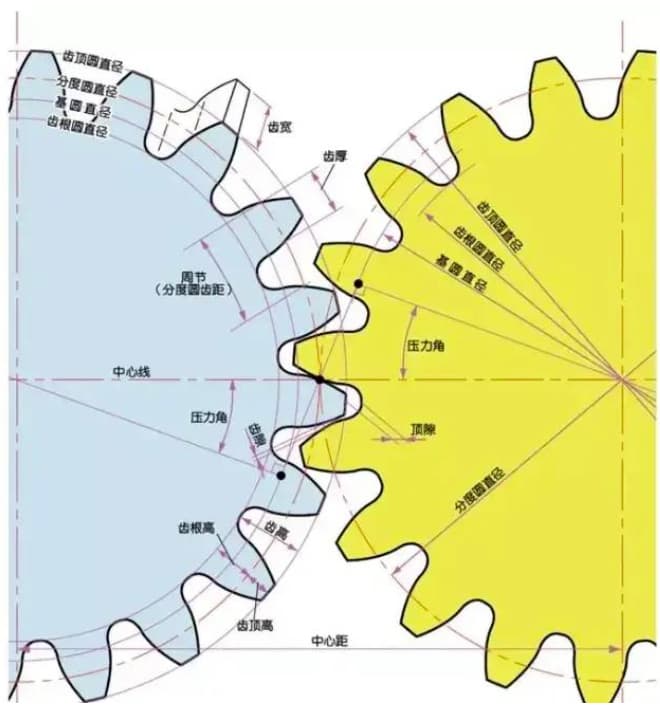
El módulo (m), el ángulo de presión (α) y el número de dientes (z) son los tres parámetros básicos de un engranaje. Sobre esta base, se calcula el tamaño de cada pieza del engranaje.
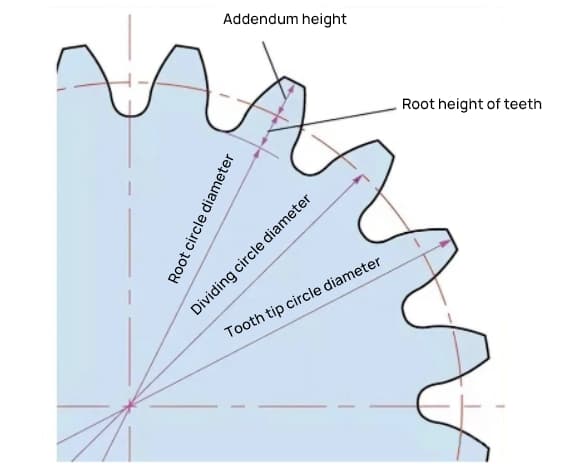
La altura de un diente de rueda dentada viene determinada por el módulo (m).
La altura del diente completo es h=2,25 m (= altura del addendum + altura del dedendum).
La altura de adición (ha) es la altura desde la punta del diente del engranaje hasta el círculo primitivo. ha=1m.
La altura del dedendum (hf) es la altura desde la raíz del diente del engranaje hasta el círculo primitivo. hf=1,25m.
La referencia para el espesor del diente del engranaje (s) es la mitad del paso. s=πm/2.
El parámetro que determina el tamaño de un engranaje es su diámetro de círculo primitivo (d). A partir del círculo primitivo, pueden determinarse el paso, el grosor, la altura, la altura de adición y la altura de deducción del engranaje.
El diámetro del círculo primitivo es d=zm.
El diámetro del círculo de adición es da=d+2m.
El diámetro del círculo dedendum es df=d-2,5m.
El círculo de paso no puede verse directamente en el engranaje real porque es un círculo supuesto que se utiliza para determinar el tamaño del engranaje.
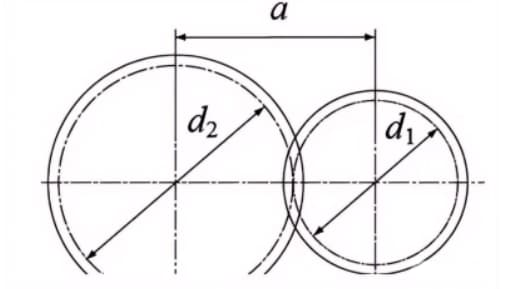
Cuando los círculos de paso de un par de engranajes engranan tangencialmente, el distancia entre centros es la mitad de la suma de los diámetros del círculo primitivo.
Distancia central a=(d1+d2)/2
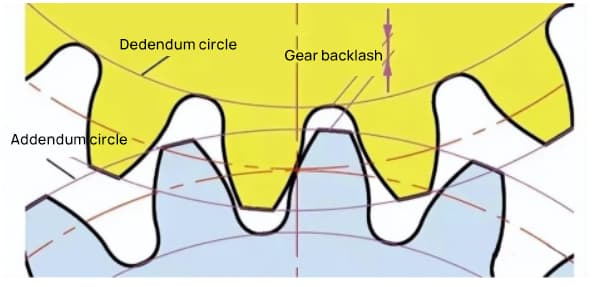
El juego es un factor importante para obtener un engrane suave de los engranajes durante el acoplamiento. Es el espacio entre las superficies de los dientes cuando un par de engranajes están engranados.
También existe un juego en la dirección de la altura del diente del engranaje. Este juego se denomina juego axial o juego (c). El juego (c) es la diferencia entre el diámetro del círculo de la raíz de un engranaje y el diámetro del círculo de la punta de su engranaje de contacto.
Distancia libre c=1,25m-1m=0,25m
Un engranaje cuyos dientes se retuercen en espiral después de un engranaje recto se denomina engranaje helicoidal. La mayoría de los cálculos geométricos de una rueda dentada recta son aplicables a una rueda dentada helicoidal. Existen dos tipos de ruedas helicoidales en función de sus superficies de referencia:
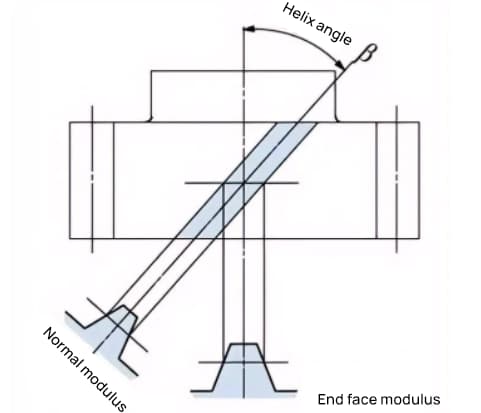
En los engranajes helicoidales, como las ruedas dentadas helicoidales y los engranajes cicloidales, cuyos dientes tienen forma helicoidal, la dirección de la hélice y el engrane son fijos.
La dirección de la hélice se refiere a cuando el eje del engranaje apunta hacia arriba y hacia abajo, la dirección de los dientes es hacia arriba a la derecha como "mano derecha", y hacia arriba a la izquierda como "mano izquierda" cuando se mira desde el frente. A continuación se muestra el engrane de varios tipos de engranajes.

Si los dientes con igual separación sólo se dividen en la periferia exterior de la rueda de fricción, se les colocan salientes y, a continuación, se engranan y giran entre sí, pueden surgir los siguientes problemas:
Cuando la transmisión debe ser silenciosa y suave, se utilizan curvas evolventes.
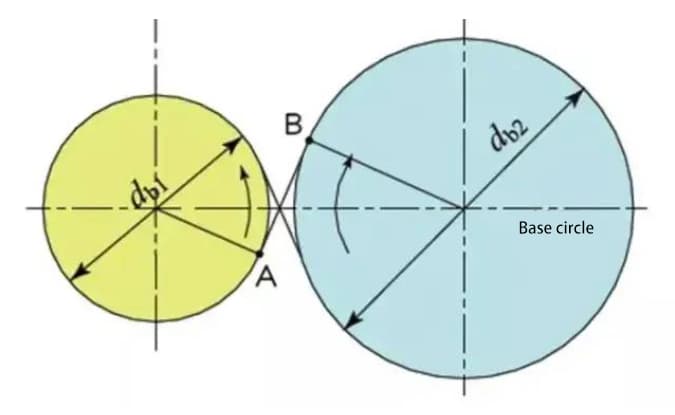
Una curva involuta es una curva que se obtiene enrollando un alambre con un lápiz en la periferia exterior de un cilindro y soltando gradualmente el alambre en estado de tensión.
La curva dibujada por el lápiz es la curva involuta, y la periferia exterior del cilindro se denomina círculo base.
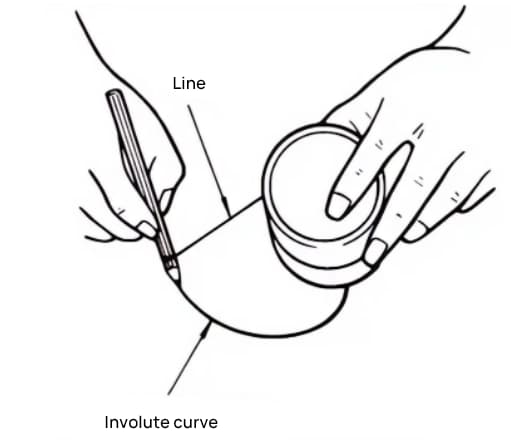
Divide el cilindro en 8 partes iguales y ata 8 lápices a ellas para dibujar 8 curvas involutivas. A continuación, enrolla los alambres en sentido contrario y dibuja 8 curvas más utilizando el mismo método. Se trata de un engranaje de 8 dientes con curvas evolventes como perfil de sus dientes.
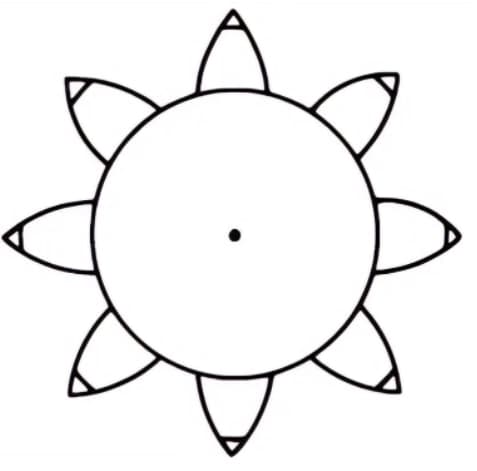
Las ventajas de los engranajes evolventes incluyen su capacidad para transmitir una relación de velocidad constante, un funcionamiento suave debido a su patrón de contacto gradualmente cambiante y una baja sensibilidad a las variaciones de la distancia entre ejes.
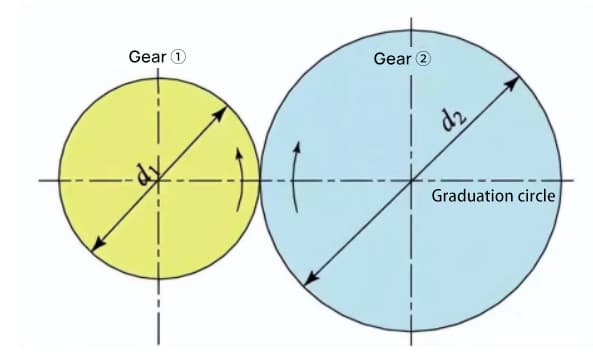
El círculo base es el círculo fundamental que forma el perfil del diente evolvente. El círculo de paso es el círculo de referencia que determina el tamaño de la rueda dentada. El círculo base y el círculo de paso son dimensiones geométricas importantes de los engranajes.
El perfil del diente en evolvente es una curva formada en el exterior del círculo base, y el ángulo de presión en el círculo base es cero.
Cuando se engranan dos ruedas evolventes estándar, sus círculos de paso son tangentes entre sí a la distancia entre ejes estándar. El aspecto del engrane de los dos engranajes se parece a la transmisión de dos ruedas de fricción con diámetros d1 y d2, respectivamente.
Sin embargo, el engrane de los engranajes evolventes depende más del círculo de base que del círculo primitivo.
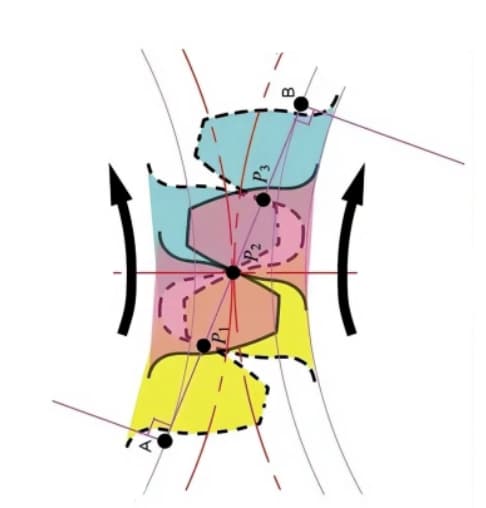
Los puntos de contacto entre los dientes de engrane de dos engranajes se mueven a lo largo de la línea de acción en la secuencia de P1, P2 y P3.
Preste atención al diente amarillo de la rueda motriz. Después de que este diente comience a engranar, el engranaje se encuentra en un estado de engrane de dos dientes (P1, P3) durante un período de tiempo. El engrane continúa y, cuando el punto de contacto se desplaza al punto P2 del círculo primitivo, sólo queda un diente engranado.
El engrane continúa, y cuando el punto de contacto se desplaza al punto P3, el siguiente diente del engranaje comienza a engranar en el punto P1, formando de nuevo un estado de engrane de dos dientes. De este modo, el engrane de dos dientes y el engrane de un solo diente de los engranajes interactúan y transmiten repetidamente el movimiento de rotación.
La línea tangente común entre los círculos de base, A-B, se denomina línea de acción. Los puntos de contacto de los pares de engranajes están todos en esta línea de acción.
Con un diagrama ilustrativo, es como una correa que discurre por las periferias exteriores de dos círculos de base y transmite energía mediante el movimiento de rotación.
El perfil del diente de los engranajes que solemos utilizar suele ser un evolvente estándar, pero también hay situaciones en las que es necesario desplazar los dientes del engranaje, como ajustar la distancia entre ejes o evitar el destalonado del engranaje más pequeño.
La curva involuta del perfil del diente varía en función del número de dientes. Cuantos más dientes haya, más tenderá la curva del perfil a una línea recta.
A medida que aumenta el número de dientes, la forma de la raíz del diente se hace más gruesa y aumenta la resistencia de la rueda dentada.
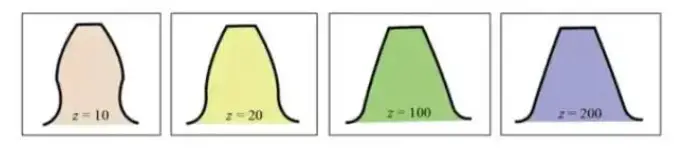
Del gráfico anterior se desprende que, para una rueda dentada con 10 dientes, se elimina parte del perfil del diente evolvente en la raíz del diente, lo que provoca una socavación.
Sin embargo, adoptando un desplazamiento positivo para la rueda dentada con z=10, aumentando el diámetro del círculo de adición e incrementando el grosor del dentado de los dientes de la rueda dentada, se puede conseguir la misma resistencia de engranaje que la de una rueda dentada con 200 dientes.
El siguiente diagrama muestra el esquema de un engranaje de 10 dientes con desplazamiento positivo. Durante el tallado de engranajes, la cantidad de movimiento de la herramienta a lo largo de la dirección radial se denomina cantidad de desplazamiento radial (denominada cantidad de desplazamiento) xm(mm).
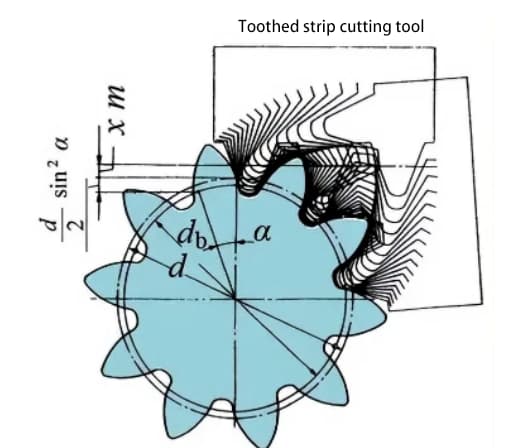
Mediante el desplazamiento positivo del perfil del diente, aumenta el espesor del diente de la rueda dentada y también aumenta el diámetro exterior (diámetro del círculo de adición).
Adoptando el desplazamiento positivo, se puede evitar la socavación de los engranajes. El desplazamiento de los engranajes también puede lograr otros fines, como cambiar la distancia entre ejes. El desplazamiento positivo puede aumentar la distancia central, mientras que el desplazamiento negativo puede reducirla.
Independientemente de si se trata de un engranaje con desplazamiento positivo o negativo, existen limitaciones en cuanto a la cantidad de desplazamiento.
El desplazamiento puede ser positivo o negativo. Aunque la altura del diente es la misma, el grosor del diente es diferente. Una rueda dentada con un espesor de diente engrosado es una rueda dentada de desplazamiento positivo, mientras que una rueda dentada con un espesor de diente reducido es una rueda dentada de desplazamiento negativo.
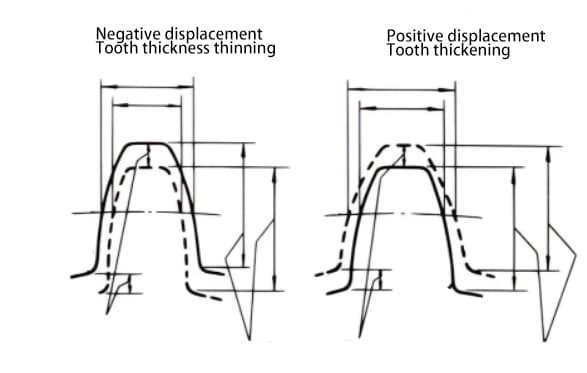
Cuando no es posible modificar la distancia central entre dos ruedas dentadas, se puede aplicar un desplazamiento positivo a la rueda dentada más pequeña (para evitar la socavación) y un desplazamiento negativo a la rueda dentada más grande, con el fin de conseguir la misma distancia central. En este caso, el valor absoluto de la cantidad de desplazamiento es igual.
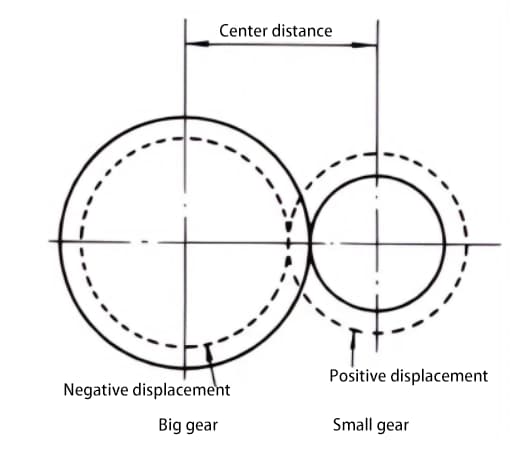
Los engranajes estándar engranan cuando sus círculos de paso son tangentes entre sí. El engrane de los engranajes desplazados, como se muestra en la figura, es tangente entre sí en el círculo de engrane.
El ángulo de presión en el círculo de engrane se denomina ángulo de engrane. El ángulo de engrane es diferente del ángulo de presión en el círculo primitivo (ángulo de presión del círculo primitivo), y es un factor importante en el diseño de engranajes desplazados.
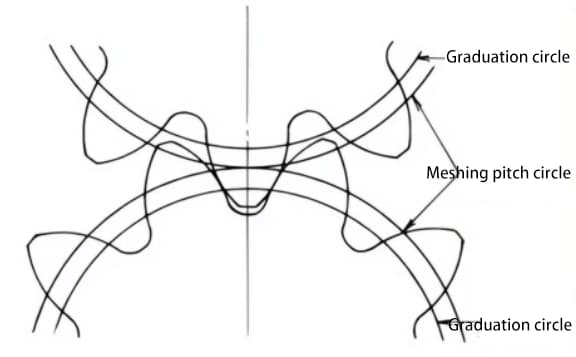
El desplazamiento del engranaje puede evitar la socavación causada por un número reducido de dientes durante el mecanizado. La distancia entre ejes deseada puede obtenerse mediante el desplazamiento.
En un par de engranajes con una gran diferencia en el número de dientes, se puede aplicar un desplazamiento positivo al engranaje más pequeño, que se desgasta con facilidad, para aumentar el grosor del diente, mientras que se puede aplicar un desplazamiento negativo al engranaje más grande para reducir el grosor del diente, con el fin de que la esperanza de vida de los dos engranajes sea más comparable.
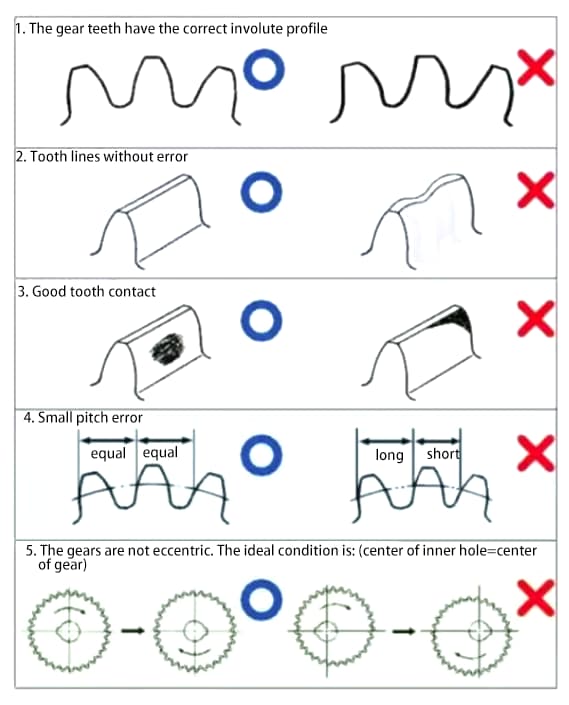
Los engranajes son componentes mecánicos que transmiten potencia y rotación. Los principales requisitos para el funcionamiento de los engranajes son:
Para cumplir los requisitos anteriores, mejorar la precisión de los engranajes se convertirá en una tarea necesaria.
La precisión de los engranajes puede dividirse a grandes rasgos en tres categorías:
a) Precisión del perfil del diente evolvente - precisión del perfil del diente
b) Precisión de la línea del flanco del diente en la superficie del diente - precisión de la línea del diente
c) Precisión de la posición de los dientes/ranuras.
El error del perfil del diente se refiere al error entre el perfil del diente real de la rueda dentada y el perfil del diente teórico.
Hay muchos factores que afectan al error del perfil del diente, como la herramienta y las vibraciones de la máquina herramienta durante el proceso de corte.
El error del perfil del diente afecta al rendimiento del engrane y al ruido. Por lo tanto, es necesario controlar el error del perfil del diente dentro del rango permitido.
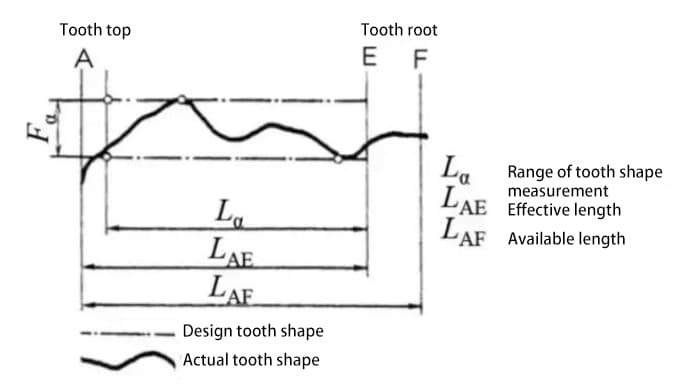
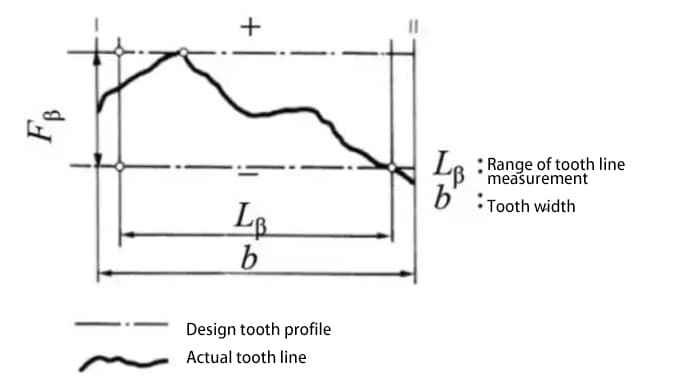
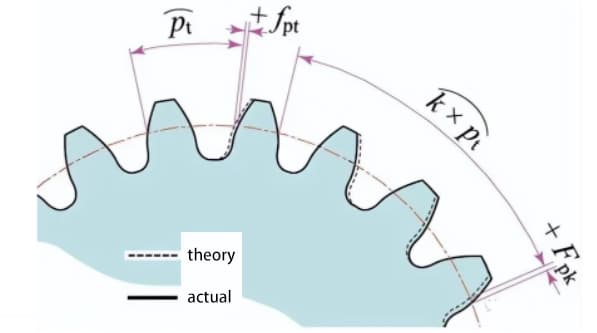
Mida el valor de paso en la circunferencia de medición centrada en el eje del engranaje.
La desviación del paso de diente único (fpt) es la diferencia entre el paso real y el paso teórico.
La desviación total acumulada del paso (Fp) se utiliza para evaluar la desviación de todo el paso del engranaje. El valor de amplitud total de la curva de desviación acumulativa del paso representa la desviación total del paso.
Coloque una sonda (esférica o cilíndrica) sucesivamente en la ranura de los dientes y mida la diferencia entre las distancias radiales máxima y mínima de la sonda al eje del engranaje. La excentricidad del eje del engranaje es uno de los factores que contribuyen a la excentricidad radial.
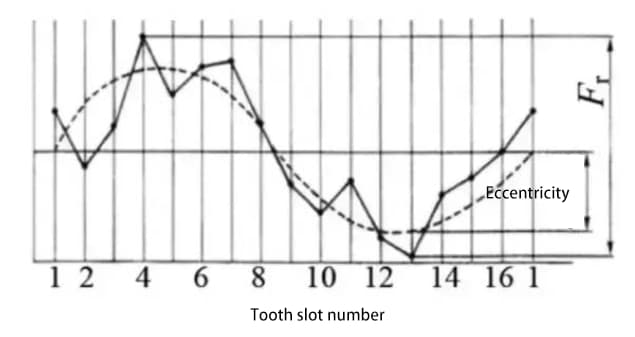
Hasta ahora, los métodos que hemos descrito para evaluar la precisión de las ruedas dentadas, como la forma del diente, el paso y la precisión del flanco del diente, son todos métodos para evaluar la precisión de una rueda dentada individual.
En cambio, existe otro método que evalúa la precisión de los engranajes realizando una prueba de engrane de dos dientes en el engranaje en combinación con un engranaje de medición. Las dos superficies de la rueda dentada probada se engranan con la rueda dentada de medición y giran durante un ciclo completo. Se registra la variación de la distancia entre ejes.
La figura siguiente muestra los resultados de la prueba para una rueda dentada con 30 dientes. Hay un total de 30 líneas de onda para la desviación compuesta radial de un solo diente.
El valor de la desviación compuesta radial es aproximadamente la suma de la desviación de excentricidad radial y la desviación compuesta radial de un solo diente.
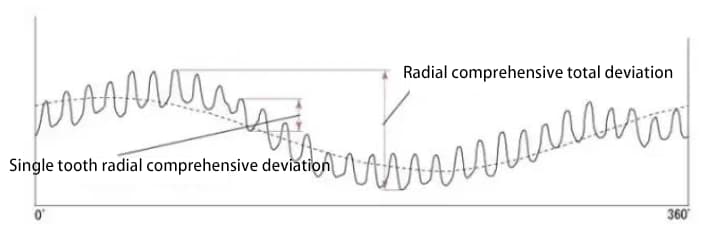
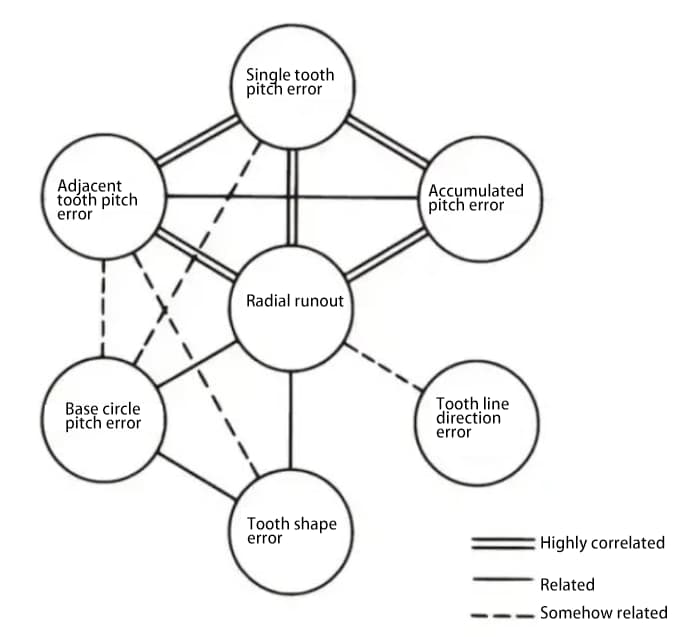
Las distintas partes de la precisión del engranaje están relacionadas entre sí. En general, la excentricidad radial está fuertemente correlacionada con otros errores, y también existe una fuerte correlación entre varios errores de paso.
Ángulo de espiral en una sección cilíndrica normal:
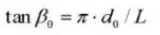
Ángulo de espiral en un cilindro de base:
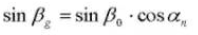
Ángulo de centrado del grosor del diente:
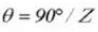
Diámetro del pasador:
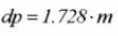
Factor de corrección de la distancia entre ejes:
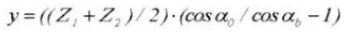
Cálculo de engranajes rectos estándar (piñón ①, rueda dentada ②)
1. Número de dientes del engranaje estándar
2. Engranaje de perfil evolvente estándar Engranaje de dientes rectos
3. Módulo m
4. Ángulo de presión
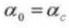
5. Número de dientes
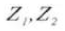
6. Profundidad efectiva del diente
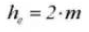
7. Profundidad total del diente
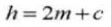
8. Holgura del piñón
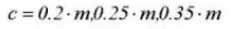
9. Diámetro del círculo de paso de referencia
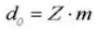
10. Diámetro exterior
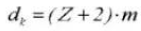
11. Diámetro de la raíz
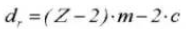
12. Diámetro del círculo base
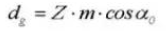
13. Paso circular
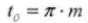
14. Paso diametral normal
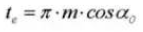
15. Espesor del diente circular
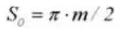
16. Espesor del diente cordal
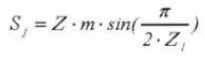
17. Altura del diente de la varilla de nivel de aceite
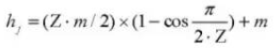
18. Número de dientes transversales
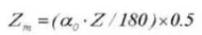
19. Grosor del diente transversal
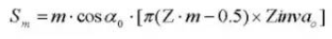
20. Diámetro del pasador
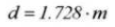
21. Dimensión cilíndrica de medición
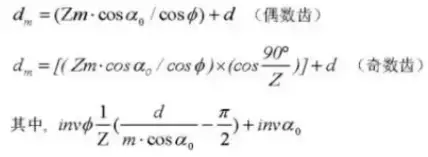
Fórmula para el cálculo de engranajes rectos desplazados (piñón ①, engranaje ②):
1. Perfil del diente del engranaje Transversal
2. Relación de contacto del perfil del diente de la herramienta
3. Módulo m
4. Ángulo de presión
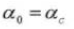
5. Número de dientes Z
6. Profundidad efectiva del diente
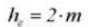
7. Profundidad total del diente
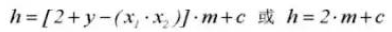
8. Juego del engranaje C
9. Relación de contacto transversal X
10. Distancia al centro
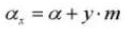
11. Diámetro del círculo de paso de referencia
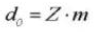
12. Ángulo de presión de funcionamiento
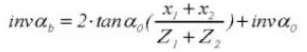
13. Diámetro del círculo primitivo
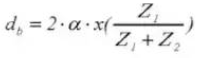
14. Diámetro exterior
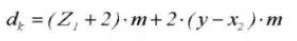
15. Adición Diámetro
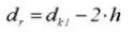
16. Diámetro de paso
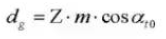
17. Paso circular
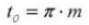
18. Paso diametral normal
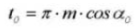
19. Espesor del diente circular
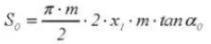
20. Grosor del diente cordal
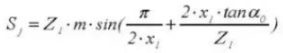
21. Altura de los dientes del calibrador Vernier de engranajes
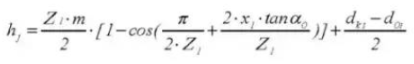
22. Número de dientes transversales
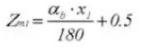
23. Grosor del diente transversal
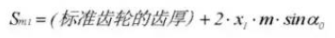
24. Diámetro de la punta
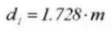
25. Dimensión de medición transversal

Fórmula de cálculo de los engranajes cilíndricos normalizados (sistema normal) (piñón ①, rueda dentada ②)
1. Perfil estándar del diente del engranaje
2. Sección de referencia del sistema normal del perfil del diente
3. Engranaje cilíndrico con perfil de diente de herramienta
4. Módulo
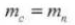
5. Ángulo de presión
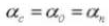
6. Número de dientes
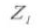
7. Dirección de la hélice
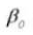
8. Profundidad efectiva del diente
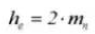
9. Profundidad total del diente
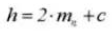
10. Ángulo de presión frontal
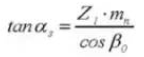
11. Distancia al centro
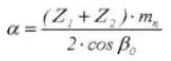
12. Diámetro del círculo de paso de referencia
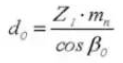
13. Diámetro exterior
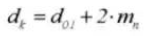
14. Diámetro de la raíz
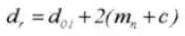
15. Diámetro de paso
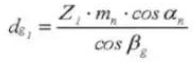
16. Ángulo de la hélice en el círculo base
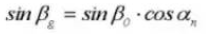
17. Pitch
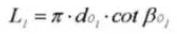
18. Paso circular (sistema normal)
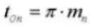
19. Paso diametral normal (sistema normal)
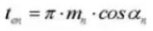
20. Espesor del diente circular (sistema normal)
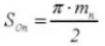
21. Número equivalente de dientes en un engranaje recto estándar
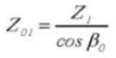
22. Espesor del diente cordal
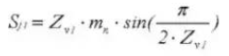
23. Profundidad de los dientes del calibrador Vernier de engranajes
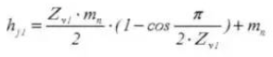
24. Número de dientes transversales
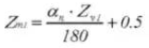
25. Espesor del diente transversal
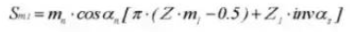
26. Diámetro de la punta
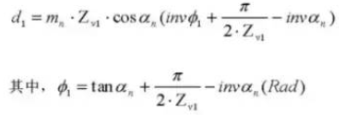
27. Dimensión cilíndrica de medición

28. Juego del engranaje f
Fórmula para el cálculo de engranajes cilíndricos desplazados (sistema normal) (piñón ①, engranaje ②):
1. Perfil del diente del engranaje desplazado
2. Sección de referencia del sistema normal del perfil del diente
3. Engranaje cilíndrico con perfil de diente de herramienta
4. Módulo (sistema normal)
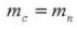
5. Ángulo de presión (sistema normal)
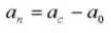
6. Número de dientes
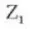
7. Dirección de la hélice
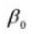
8. Profundidad efectiva del diente
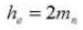
9. Profundidad total del diente
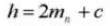
10. Relación de contacto transversal
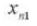
11. Distancia al centro
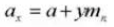
12. Módulo normal
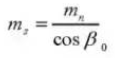
13. Ángulo de presión frontal (sistema normal)
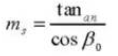
14. Número equivalente de dientes en un engranaje recto estándar
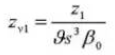
15. Ángulo de presión normal del sistema
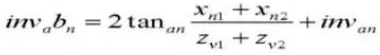
16. Diámetro del círculo de paso de referencia
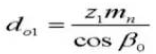
17. Diámetro exterior
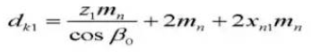
18. Diámetro de paso de los dientes en contacto
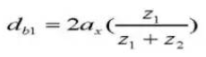
19. Diámetro de paso
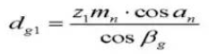
20. Ángulo de hélice en el cilindro base
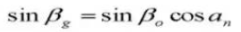
21. Espesor del diente circular
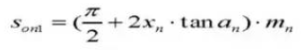
22. Espesor del diente cordal
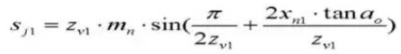
23. 23. Altura de los dientes del calibrador Vernier de engranajes.
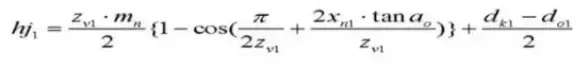
24. Número de dientes transversales
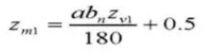
25. Espesor del diente transversal

26. Diámetro del pasador.
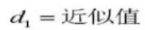
27. Dimensión cilíndrica de medición