¿Alguna vez se ha preguntado cómo garantizan los diseñadores de chapa metálica la precisión de sus diseños? En esta entrada del blog, nos adentraremos en el fascinante mundo del diseño de chapa metálica y exploraremos dos conceptos esenciales: la tolerancia de plegado y la deducción de plegado. También presentaremos el factor K y su papel en los cálculos. Acompáñenos para desentrañar estos temas y conocer las valiosas opiniones de los expertos del sector.
En el campo del diseño de chapas metálicas, términos como tolerancia de plegado, deducción de plegado y factor K son conceptos cruciales que influyen significativamente en la precisión y la eficacia de los procesos de fabricación. Estos parámetros desempeñan un papel fundamental a la hora de determinar las dimensiones finales de las piezas de chapa doblada y garantizar una fabricación precisa. Profundicemos en estos conceptos y exploremos sus métodos de cálculo.
Los ingenieros y fabricantes que se dedican a la fabricación de chapas metálicas utilizan sofisticados algoritmos para calcular con precisión las dimensiones planas de las piezas, lo que garantiza geometrías finales precisas tras las operaciones de plegado y conformado.
El "método del pellizco" tradicional sigue siendo un enfoque empírico muy utilizado, que incorpora factores como las propiedades del material, el radio de curvatura, el ángulo de curvatura, las configuraciones de las herramientas y las velocidades de conformado. Este método, aunque eficaz, depende en gran medida de la experiencia del operario y puede estar sujeto a incoherencias.
Con la llegada de herramientas computacionales avanzadas, el diseño asistido por ordenador (CAD) y el análisis de elementos finitos (FEA) han revolucionado la precisión y eficacia del diseño de chapas metálicas. Estas tecnologías permiten simular con precisión el comportamiento de los materiales durante los procesos de conformado, teniendo en cuenta fenómenos complejos como el springback, las tensiones residuales y el endurecimiento por deformación.
Los sistemas CAD modernos emplean algoritmos avanzados de compensación de curvatura que integran modelos teóricos con datos empíricos. Estos algoritmos suelen utilizar uno de los dos enfoques principales:
Las principales plataformas CAD, como SolidWorks, Autodesk Inventor y Siemens NX, ofrecen sólidos módulos de diseño de chapa metálica con tablas de plegado y bibliotecas de materiales personalizables. Estos sistemas permiten integrar datos de plegado específicos del taller, lo que garantiza la alineación entre los diseños digitales y los procesos de fabricación reales.
Además, se están aplicando tecnologías emergentes como el aprendizaje automático y la inteligencia artificial para optimizar los cálculos de plegado, aprovechando vastos conjuntos de datos históricos de producción para refinar las predicciones y adaptarse a combinaciones únicas de materiales y herramientas.
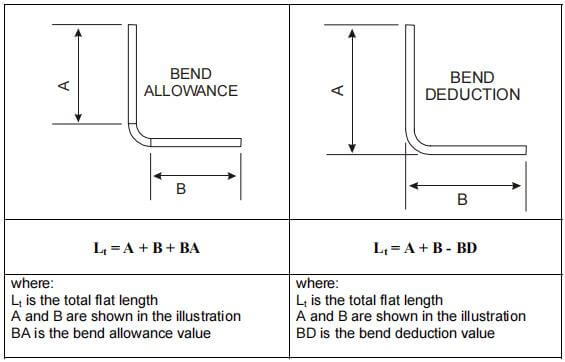
Para que los lectores comprendan mejor los conceptos básicos del diseño de chapa cálculo, se resumirán y explicarán los siguientes puntos:
Para comprender mejor margen de flexiónEn la figura 1 se ilustra la curvatura de una pieza de chapa metálica. La figura 2 muestra la pieza en su estado desplegado.
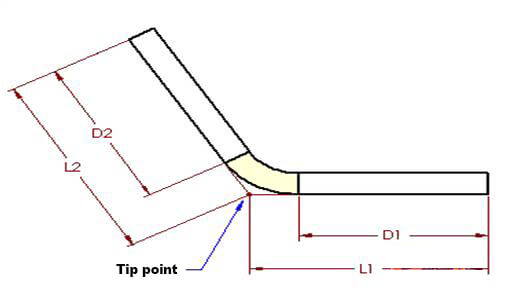
Figura 1
Figura 2
El algoritmo de sobremedida de plegado describe la longitud desplegada (LT) de una pieza de chapa metálica como la suma de las longitudes de cada segmento después de aplanar la pieza, más la longitud del área de plegado aplanada.
En margen de flexión (BA) representa la longitud de la zona de flexión aplanada. Así pues, la longitud total de la pieza puede expresarse mediante la ecuación (1):
LT = D1 + D2 + BA (1)
La zona de flexión (representada en amarillo claro en la ilustración) es la zona que teóricamente sufre una deformación durante el proceso de flexión.
Para determinar la geometría de la pieza desplegada, siga estos pasos:
La tarea de determinar la longitud de la zona de flexión aplanada, representada por BA en la figura, es un poco más difícil.
El valor de BA varía en función de factores como el tipo de material y su grosor, radio de curvatura y el ángulo, así como el proceso de plegado, el tipo de máquina y la velocidad de ésta.
El valor de BA puede obtenerse de diversas fuentes, incluidos los proveedores de materiales de chapa metálica, datos experimentales, experiencia y manuales de ingeniería.
En SolidWorks, se pueden introducir directamente los valores BA o utilizar el factor K (que se tratará más adelante) para calcular los valores.
En mesa de doblado es la forma más precisa de especificar diferentes tolerancias de flexión para diferentes situaciones con diferentes espesores, radios y ángulos.
Crear la mesa de plegado inicial puede llevar algún tiempo, pero una vez formada, se pueden reutilizar partes de ella en el futuro.
Se puede introducir la misma información o información diferente para cada pliegue de la pieza.
1) Normas para la flexión común
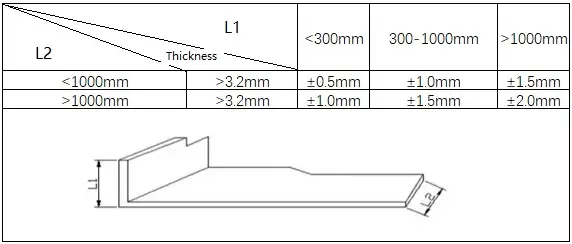
2) Normas para la flexión en Z
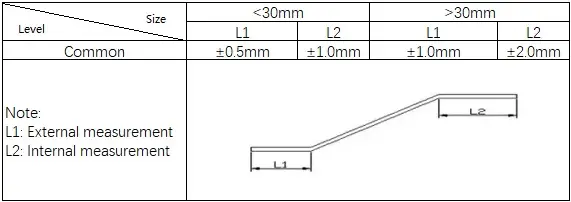
3) Normas para la flexión en V
4) Normas para Doblado en U
Lectura relacionada: Calculadora de fuerza de flexión en V y en U
La deducción por flexión es un término utilizado para describir la cantidad de retroceso en el proceso de plegado de chapa. Este es otro algoritmo sencillo para describir el proceso.
Las figuras 1 y 2 también se aplican a este concepto. Según el método de la deducción por flexión, la longitud aplanada (LT) de la pieza es igual a la suma de las longitudes de las dos secciones planas que se extienden hasta el "punto de punta" (la hipotética intersección de las dos secciones planas), menos la deducción por flexión (BD).
Así, la longitud total de la pieza puede expresarse como se indica en la ecuación (2):
LT = L1 + L2 - BD (2)
El valor de BD puede determinarse u obtenerse de diversas fuentes, como la hoja material metálico proveedores, datos experimentales, experiencia, manuales de ingeniería con ecuaciones o tablas, etc.
Figura 3
Es importante que los usuarios familiarizados con el método de deducción por flexión comprendan la relación con el método de subsidio por flexión, que se adopta habitualmente en SolidWorks.
La relación entre ambos valores puede deducirse fácilmente utilizando las dos geometrías de flexión y despliegue de piezas.
Comparando las ecuaciones (1) y (2), tenemos:
LT = D1 + D2 + BA (1) LT = L1 + L2 - BD (2)
Y por lo tanto,
D1 + D2 + BA = L1 + L2 - BD (3)
En la figura 3, el ángulo A representa el ángulo de flexión, que describe el ángulo barrido por la pieza durante el plegado, y también el ángulo del arco formado por la zona de plegado, que se muestra en dos mitades.
Utilizando las dimensiones y los principios de los triángulos rectángulos, podemos obtener las siguientes ecuaciones:
D1 = L1 - (R + T)TAN(A/2) (4) D2 = L2 - (R + T)TAN(A/2) (5)
Sustituyendo las ecuaciones (4) y (5) en la ecuación (3), podemos obtener la relación entre BA y BD:
BA = 2(R + T)TAN(A/2) - BD (6)
Y cuando el ángulo de flexión es de 90 grados, esta ecuación se simplifica a:
BA = 2(R + T) - BD (7)
Estas ecuaciones (6) y (7) proporcionan un método conveniente para convertir de un algoritmo a otro, utilizando únicamente como parámetros el espesor del material, el ángulo/radio de flexión, etc.
Para los usuarios de SolidWorks, estas ecuaciones proporcionan un método directo para convertir la Deducción de pliegue en Tolerancia de pliegue.
El valor de la tolerancia de plegado puede utilizarse para toda la pieza o para cada plegado individual, o puede incluirse en una tabla de datos de plegado.
El factor K es un valor independiente que explica la flexión y el despliegue de la chapa metálica en diversos escenarios geométricos.
También es un valor autónomo que se utiliza para calcular la tolerancia de flexión (BA) en diversas condiciones, como diferentes espesores de material, ángulos de flexión y radios.
Las figuras 4 y 5 sirven para aclarar la definición detallada del factor K.
Figura 4
Gráfico 5
Podemos confirmar que existe un eje neutro en el espesor de la pieza de chapa. La chapa material metálico en este eje neutro en la región de flexión no se estira ni se comprime, lo que significa que es la única zona que no se deforma durante la flexión.
Las figuras 4 y 5 muestran el límite entre las regiones rosa y azul.
Durante el plegado, la región rosa se comprime y la azul se extiende. Si la capa de chapa neutra permanece sin deformar, la longitud de su arco en la región de flexión sigue siendo la misma tanto si la pieza se dobla como si se aplana.
Como resultado, la sobremedida de flexión (BA) debe ser igual a la longitud del arco de la capa neutra en la región de flexión de la pieza de chapa, que se muestra en verde en la figura 4.
La posición de la capa neutra de la chapa depende de las propiedades de un material concreto, como la ductilidad.
Se supone que la distancia entre la capa de chapa neutra y la superficie es "t", o la profundidad desde la superficie de la pieza de chapa hacia el interior del material en la dirección del espesor.
Como resultado, el radio del arco de la capa neutra puede expresarse como (R + t). Utilizando esta expresión y el ángulo de flexión, se puede calcular la longitud del arco de la capa neutra (BA).
BA = Pi(R+T)A/180
Para simplificar la definición de la capa neutra de la chapa y hacerla aplicable a todos los materiales, se introdujo el concepto de factor K.
La definición del factor K es: es la relación entre el espesor de la capa neutra de la chapa y el espesor total del material de la pieza de chapa. En otras palabras, el factor K se define como:
K = t/T
Por lo tanto, el valor de K estará siempre comprendido entre 0 y 1. Si el factor K es 0,25, indica que la capa neutra está situada a 25% del espesor total del material de la chapa.
Asimismo, si es 0,5, significa que la capa neutra se encuentra a 50% de todo el espesor, y así sucesivamente.
Combinando las ecuaciones anteriores, se obtiene la siguiente ecuación (8):
BA = Pi(R+K*T)A/180 (8)
Por lo tanto, el valor de K estará siempre entre 0 y 1.
Si el factor K es 0,25, significa que la capa neutra está situada a 25% del espesor del material de la chapa de la pieza.
Del mismo modo, si es 0,5, significa que la capa neutra se encuentra a 50% de todo el espesor, y así sucesivamente.
El origen del factor K se remonta a fuentes tradicionales como proveedores de materiales de chapa, datos de ensayos, experiencia, manuales, etc.
Sin embargo, en algunos casos, el valor proporcionado puede no expresarse como un factor K claro, pero aun así es posible encontrar la relación entre ellos.
Por ejemplo, si un manual o literatura describe el eje neutro como "posicionado a 0,445x espesor del material desde la superficie de la chapa", puede interpretarse como un factor K de 0,445, lo que significa k = 0,445.
Si se sustituye este valor de K en la ecuación (8), se obtiene la siguiente fórmula.
BA = A (0,01745R + 0,00778T)
Si se modifica la ecuación (8) por otro método, se calcula la constante de la ecuación (8) y se mantienen todas las variables, se obtiene lo siguiente:
BA = A (0,01745 R + 0,01745 K*T)
Comparando las dos ecuaciones, es fácil determinar que 0,01745 * k = 0,00778, por lo que se puede calcular que k es 0,445.
Se ha descubierto que el sistema SolidWorks también proporciona un algoritmo de tolerancia a la flexión para materiales específicos cuando el ángulo de flexión es de 90 grados. La fórmula de cálculo para cada material es la siguiente:
De hecho, simplificando la ecuación (7) y fijando el ángulo de flexión en 90 grados, se puede calcular la constante y transformar la ecuación como sigue:
BA = (1,57 * K * T) + (1,57 *R)
Por lo tanto, comparando la fórmula de cálculo anterior, el valor de K para materiales de latón blando o cobre blando puede obtenerse como 1,57xk = 0,55, o K = 0,35.
Utilizando el mismo método, es fácil calcular los valores del factor K para los diversos tipos de materiales enumerados anteriormente.
Como se ha comentado anteriormente, existen varias fuentes de las que se puede obtener el valor del factor K, como proveedores de materiales, datos de ensayos, experiencia y manuales.
Para establecer un modelo de chapa metálica preciso utilizando el método del factor K, es crucial encontrar la fuente adecuada de factor K que cumpla sus requisitos de ingeniería. Esto garantizará que los resultados de la pieza física sean tan precisos como se desea.
En algunas situaciones, puede que no sea posible obtener resultados precisos utilizando un único valor de factor K, especialmente cuando es necesario acomodar una amplia gama de escenarios de flexión.
En tales casos, es aconsejable utilizar el valor de la tolerancia de flexión (BA) directamente para una sola curva de toda la pieza, o utilizar una tabla de curvatura para describir los diferentes valores de BA, deducción por flexión (BD) o factor K correspondientes a diferentes valores de A, R y T en todo el rango.
Además, se pueden utilizar ecuaciones para generar datos como la tabla de pliegues de muestra proporcionada por SolidWorks. Si es necesario, las celdas de la tabla de pliegues también pueden modificarse basándose en datos experimentales o empíricos.
El directorio de instalación de SolidWorks incluye tablas de sobremedida de pliegue, tablas de deducción de pliegue y tablas de factor K, que pueden editarse y personalizarse según sea necesario.
Este artículo ofrece una visión general de los métodos de cálculo más comunes y sus principios subyacentes utilizados en el diseño y la fabricación de piezas de chapa metálica.
Abarca el cálculo de los subsidios por flexión, las deducciones por flexión y los factores K, y explica las diferencias entre estos métodos y sus interrelaciones.
Sirve de referencia útil para ingenieros y profesionales técnicos del sector.
Nota:
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
AR 
DE 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO