¿Alguna vez se ha preguntado por qué un puente puede empezar a temblar violentamente de repente o por qué una copa de vino se rompe cuando un cantante da una nota alta? Este blog explora los fascinantes conceptos de frecuencia natural y frecuencia de resonancia, revelando cómo afectan a todo, desde las maravillas de la ingeniería hasta los objetos cotidianos. Descubra los secretos de estas vibraciones y aprenda cómo dan forma a nuestro mundo.
En el análisis cotidiano, a menudo confundimos frecuencia natural y frecuencia de resonancia, y pensamos que son lo mismo.
De hecho, esto no es riguroso.
La frecuencia natural es el comportamiento de las características naturales estructurales, mientras que la frecuencia de resonancia es el comportamiento de la respuesta estructural bajo fuerzas externas.
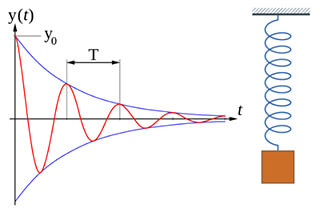
Un sistema de un solo grado de libertad es un sistema en el que la posición puede determinarse completamente mediante una sola coordenada generalizada en un momento dado. En términos más sencillos, la fuerza que actúa sobre un cuerpo lo hace en una sola dirección. El movimiento de la muñeca de la figura siguiente puede representarse como un sistema muelle-masa.
En la siguiente figura se muestra un modelo simplificado del sistema masa-muelle.
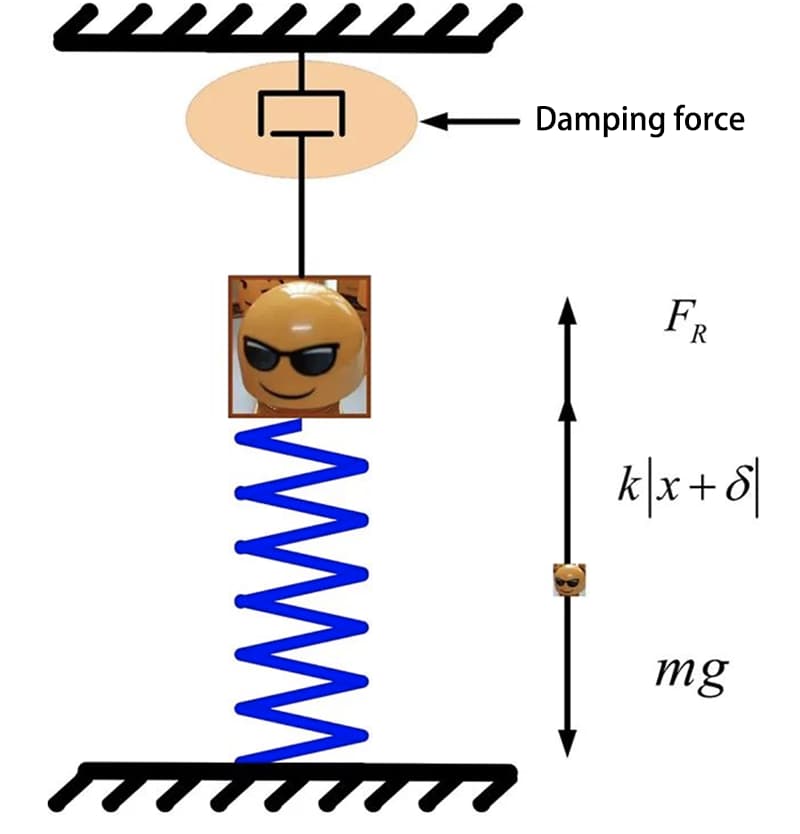
La posición de equilibrio estático del bloque de recogida se considera el origen de coordenadas, y se considera positiva cuando se mueve verticalmente hacia abajo a lo largo de la dirección de deformación del muelle. La distancia entre el bloque y la posición de equilibrio puede representarse como x, y la ecuación diferencial de movimiento para el bloque puede expresarse como:
Donde, m es la masa del bloque, k es la rigidez del muelle, c es el coeficiente de viscosidad, 2n=c/m es el coeficiente de atenuación del amortiguamiento, y cuando el coeficiente de amortiguamiento es cero, corresponde al sistema de vibración no amortiguado.
Frecuencia natural Pn:
La frecuencia natural sólo depende de la masa y la rigidez, y no se ve afectada por factores como la amortiguación. Conexiones estructurales, propiedades del materialEl diseño, la forma y otros factores pueden influir en la frecuencia natural, pero estas influencias se reflejan en la rigidez y la masa y no son los factores determinantes en última instancia.
La vibración libre es la vibración del sistema sin excitación externa, y la pista de movimiento está relacionada con el estado inicial y las características naturales.
La vibración forzada se refiere a la vibración generada por el sistema bajo excitación externa.
La excitación externa es generalmente una función periódica o aperiódica del tiempo, entre las cuales la excitación armónica simple es la más sencilla.
Sea la fuerza excitadora armónica simple:
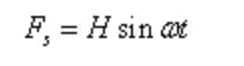
Donde, H es la amplitud de la fuerza excitante, ω es la frecuencia angular de la fuerza excitante.
Cuando el bloque se desvía de la posición de equilibrio una distancia x, la ecuación diferencial del movimiento del bloque es
Donde, h=H/m, la ecuación anterior es la ecuación diferencial de vibración forzada de un solo grado de libertad con amortiguamiento viscoso, que es una ecuación diferencial ordinaria lineal no homogénea de coeficiente constante de segundo orden.
La ecuación anterior es totalmente coherente con la expresión de respuesta de tensión de carga capacitiva que hemos aprendido en teoría de circuitos, que es una ecuación diferencial ordinaria lineal no homogénea de coeficiente constante de segundo orden.
La amortiguación del circuito depende de la resistencia, ya que ésta sólo consume y no almacena energía.
Bajo excitación armónica simple, la solución total de la ecuación diferencial de movimiento de un sistema amortiguado se establece como:
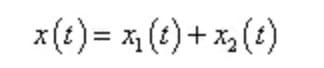
Donde, x1 (t) es una solución homogénea, que es vibración libre atenuada;
Debido a la existencia de amortiguación, la parte de vibración amortiguada desaparecerá al cabo de cierto tiempo.
Su solución es la misma que la de la vibración libre, por lo que no se repetirá aquí.
Aquí nos interesa la solución especial x2 (t) generada por la vibración forzada, que puede expresarse como:
Entre ellas,
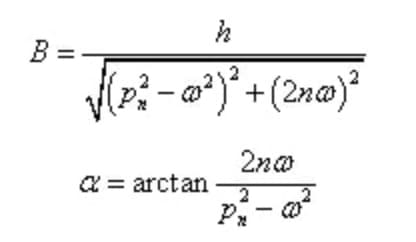
La amplitud y el desfase de la vibración forzada en estado estacionario son independientes de las condiciones iniciales, sólo dependen de las características del sistema y de la excitación.
Ajuste la relación de frecuencia, la relación de amortiguación y el coeficiente de amplificación de amplitud como:
La fórmula anterior puede reescribirse como:
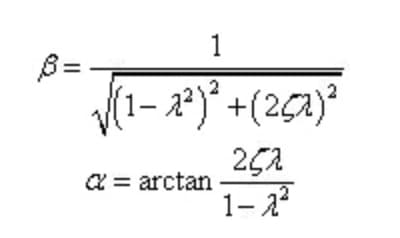
En base a esto, podemos conocer la respuesta del sistema bajo la vibración forzada.
Para una mejor comprensión, se puede ilustrar la relación entre diferentes coeficientes de amortiguación, coeficientes de frecuencia y coeficientes de amplificación de la amplitud. La frecuencia se divide en tres regiones: baja frecuencia, media frecuencia y alta frecuencia. Como se ve en la figura, tanto en la zona de baja frecuencia como en la de alta frecuencia, la amortiguación tiene un impacto mínimo en el coeficiente de amplificación de la amplitud. Así, el sistema amortiguado puede simplificarse como un sistema no amortiguado para facilitar el cálculo.
La frecuencia natural es una característica inherente a las propiedades estructurales de un sistema, determinada únicamente por su masa y rigidez, independientemente de factores externos como la amortiguación. En un sistema de n grados de libertad, existen n frecuencias naturales distintas, mientras que los sistemas continuos poseen un número infinito de frecuencias naturales.
La resonancia se produce cuando una frecuencia de excitación externa se aproxima o coincide con la frecuencia natural de un sistema, provocando que la estructura vibre con una amplitud significativamente mayor. Este fenómeno está representado por el círculo azul de la figura adjunta. La frecuencia de resonancia, aunque suele aproximarse a la frecuencia natural en sistemas poco amortiguados, puede desviarse de ella en estructuras muy amortiguadas, siendo normalmente inferior a la frecuencia natural.
En el diseño del sistema, es crucial evitar no sólo la frecuencia de pico de resonancia específica, sino también la banda de resonancia circundante, correspondiente a la región de frecuencia intermedia de la figura. Esta precaución es necesaria porque la respuesta del sistema se amplifica considerablemente dentro de esta banda. Los ingenieros deben asegurarse de que ni el funcionamiento normal del sistema ni las excitaciones externas de los equipos cercanos entren en este rango crítico.
La resonancia puede tener profundas implicaciones, tanto beneficiosas como perjudiciales. Los efectos negativos pueden incluir el colapso de vigas elevadoras, resonancia en tierra en helicópteros, daños en maquinaria y fallos estructurales inducidos por infrasonidos. A la inversa, la resonancia se utiliza deliberadamente en instrumentos musicales para producir tonos y armónicos deseados.
Para mitigar los riesgos asociados a la resonancia, los diseñadores emplean diversas estrategias:
Comprender y gestionar la resonancia es esencial en campos que van desde la ingeniería civil y aeroespacial hasta la fabricación de precisión y el diseño de instrumentos musicales. Las herramientas analíticas avanzadas, como el análisis de elementos finitos y el análisis modal experimental, desempeñan un papel crucial en la predicción y caracterización del comportamiento resonante en sistemas complejos.
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
AR 
DE 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO