¿Ha pensado alguna vez en las fuerzas que intervienen al doblar una tubería? En este artículo exploraremos el fascinante mundo de la mecánica del curvado de tubos. Nuestro experto ingeniero mecánico desglosará los conceptos clave y los cálculos implicados, proporcionando información valiosa tanto para profesionales como para aficionados. Prepárese para descubrir la ciencia que hay detrás de la creación de curvas suaves y precisas en las tuberías.
El proceso de curvado de tubos ha evolucionado significativamente con el auge de diversas industrias como la automovilística, la motociclista, la ciclista y la petroquímica. Este proceso es esencial para crear curvas precisas y duraderas en los tubos utilizados en estos sectores.
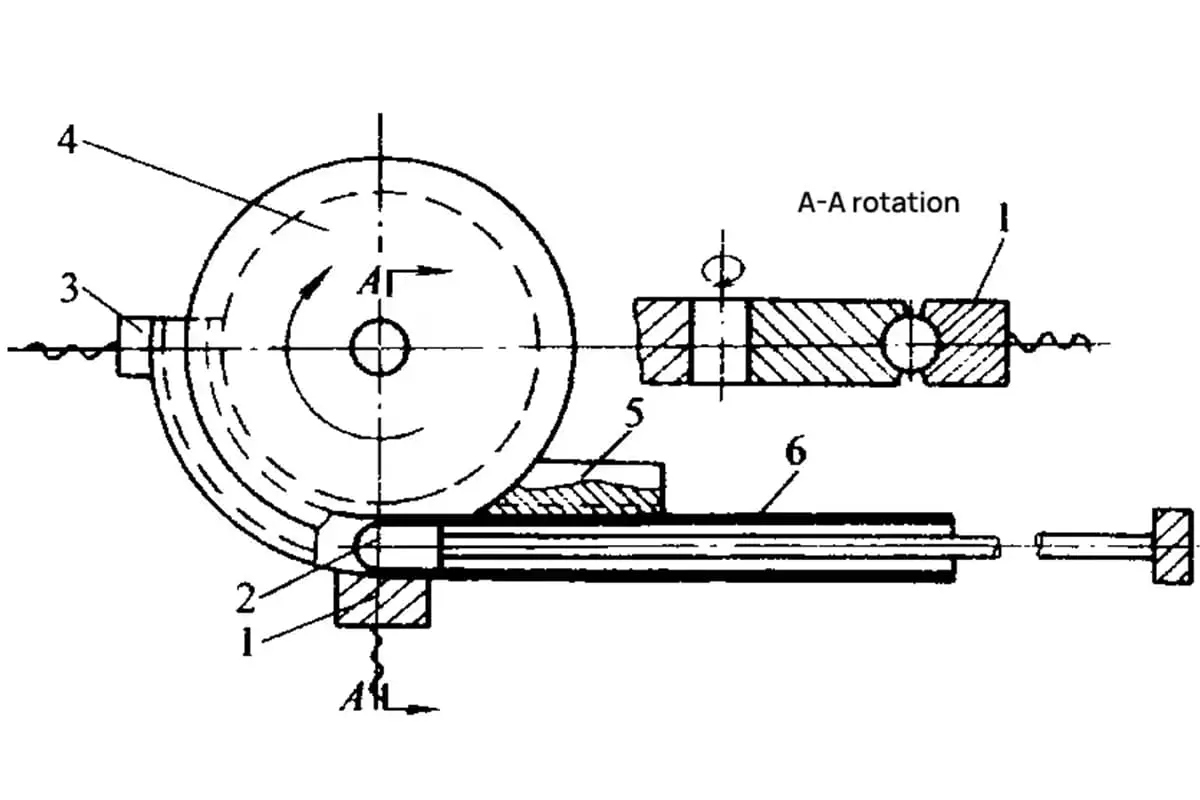
Las Figuras 6-19, 6-20, 6-21 y 6-22 representan respectivamente los diagramas esquemáticos de los moldes para los dispositivos de enrollado, empuje, prensado y enrollado. Estos diagramas ilustran la configuración específica y los componentes utilizados en cada método de doblado, proporcionando una referencia visual para la comprensión del proceso.
Al clasificar los métodos de curvado de tubos en función de la técnica de curvado, la temperatura y el uso de rellenos o mandriles, podemos comprender mejor las aplicaciones adecuadas y las ventajas de cada método. Este conocimiento es crucial para seleccionar el proceso de curvado adecuado a las necesidades industriales específicas, garantizando la eficiencia y la precisión en la fabricación.

1- Bloque de presión
2- Varilla de núcleo
3- Bloque de sujeción
4- Molde de plegado
5- Bloque antiarrugas
6- Tubería En blanco

Columna de 1 pulsación
Manguito de 2 guías
3 tubos ciegos
Molde de plegado 4

1-muere
2 tubos ciegos
Puñetazo 3-Swinging

1 eje
2,4,6 Rodillos
Eje 3-Activo
5-Tubo de acero
Cuando se dobla el material de la tubería, el material del lado exterior de la zona de deformación se estira y alarga por la tensión tangencial, mientras que el material del lado interior se comprime y acorta por la compresión tangencial.
Como la tensión tangencial σθ y la deformación εθ se distribuyen de forma continua a lo largo de la sección transversal del material de la tubería, pueden imaginarse como similares a la flexión del material de la placa.
La zona de estiramiento en el lado exterior pasa a la zona de compresión en el lado interior, con una capa neutra en la unión.
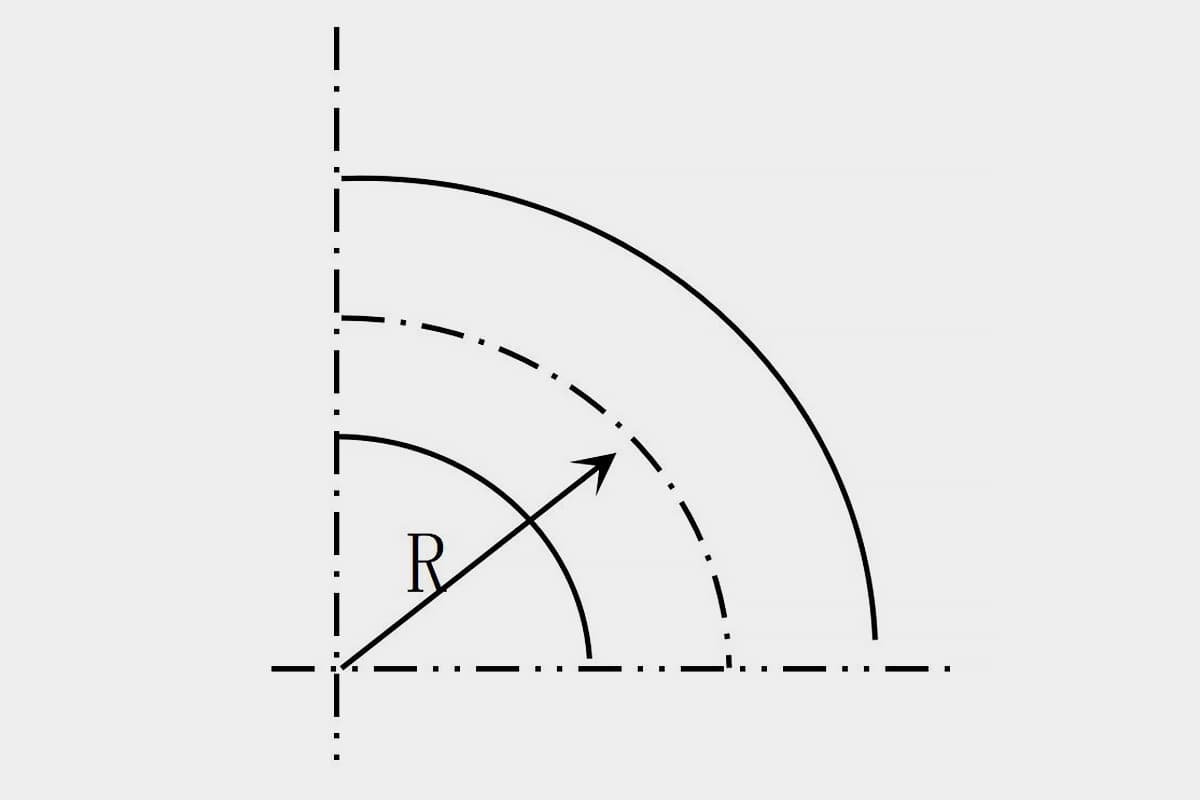
Para simplificar el análisis y el cálculo, se suele considerar que la capa neutra coincide con la capa central de la sección transversal de la tubería, y su posición en la sección transversal puede representarse por el radio de curvatura (Figura 6-23).
El grado de deformación por flexión del material de la tubería depende de la relativa radio de curvatura R/D y espesor relativo t/D (R es el radio de curvatura de la capa central de la sección transversal del tubo, D es el diámetro exterior del tubo, t es el espesor de la pared del tubo).
Cuanto menores sean los valores de R/D y t/D, mayor será el grado de deformación por flexión (es decir, R/D y t/D son demasiado pequeños), la pared exterior de la capa neutra de flexión se volverá excesivamente delgada, e incluso provocará la rotura; la pared más interna del tubo se engrosará, e incluso se volverá inestable y arrugada.
Al mismo tiempo, con el aumento del grado de deformación, la distorsión de la sección transversal (aplanamiento) se hace más grave.
Por lo tanto, para garantizar la calidad de conformado del material del tubo, el grado de deformación debe controlarse dentro del rango admisible.
El grado de deformación admisible en el curvado de tubos se denomina límite de curvado. El límite de deformación por flexión del material de la tubería no sólo depende de las propiedades mecánicas del material y del método de flexión, sino que también tiene en cuenta los requisitos de uso de los accesorios de tubería.
Para las piezas curvadas de uso general, la tensión máxima de alargamiento εmax producida en la posición más alejada de la capa neutra en el lado exterior de la zona de deformación por flexión del material de la tubería no debe superar el valor límite permitido por la plasticidad del material como condición para definir el límite de conformación.
Es decir, el radio de curvatura límite rmin que se puede doblar en el lado interior de la pieza bajo la condición de que la capa de la superficie exterior en el lado exterior de la zona de deformación de doblado de la pieza de tubería no se agriete, se utiliza como límite de formación del doblado de la pieza de tubería.
rmin está relacionada con las propiedades mecánicas del material, el tamaño estructural de los accesorios de tubería, el método de procesamiento del curvado y otros factores.

a Condiciones de fuerza
b Condiciones de tensión-deformación
El mínimo radio de curvatura para diferentes procesos de plegado se pueden encontrar en la Tabla 6-2.
Tabla 6-2 Radio mínimo de curvatura durante el curvado de tubos (Unidad: mm)
| Métodos de plegado | Radio mínimo de curvatura |
| Prensas plegadoras | (3~5)D |
| Doblado de envolturas | (2~2.5)D |
| Curvado de rodillos | 6D |
| Flexión por empuje | (2.5~3)D |
Nota: D representa el diámetro exterior del tubo.
Para el radio de curvatura mínimo de acero y tubos de aluminio, consulte la Tabla 6-3.
Tabla 6-3 Radio de curvatura mínimo de los tubos de acero y aluminio (Unidad: mm)
| Diámetro exterior del tubo | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| Radio mínimo de curvatura | 8 | 12 | 16 | 20 | 28 | 32 | 40 | 45 | 50 | 56 |
| Diámetro exterior del tubo | 24 | 28 | 30 | 32 | 35 | 38 | 40 | 44 | 48 | 50 |
| Radio mínimo de curvatura | 68 | 84 | 90 | 96 | 105 | 114 | 120 | 132 | 144 | 150 |
Durante el curvado de tubos, la distorsión de la forma de la sección transversal es inevitable.
El material de la cara exterior de la capa neutra sufre una tensión tangencial de tracción que adelgaza la pared de la tubería; el material de la cara interior de la capa neutra sufre una tensión tangencial de compresión que engrosa la pared de la tubería.
El material de los lados exterior e interior de la zona de deformación por flexión sufre la mayor tensión tangencial, por lo que allí se producen los mayores cambios en el espesor de la pared del tubo (Fig. 6-24).
En la flexión con rellenos o varillas de núcleo, la sección transversal puede mantener básicamente una forma circular, pero el grosor de la pared cambia. En la flexión sin soporte flexión libreTanto en el borde interior como en el exterior, la sección transversal circular del tubo se convierte en elíptica (Fig. 6-24a, b).
Además, a medida que aumenta el grado de deformación por flexión (es decir, disminuye el radio de flexión), el borde interior se vuelve inestable y se arruga. En el caso de los tubos cuadrados en flexión apoyada (Fig 6-24c, d), la sección transversal cambia a una forma trapezoidal.

La elipticidad se utiliza a menudo en producción para medir los cambios en la sección circular de un tubo.
Elipticidad= Dmax-Dmin/D ×100% (6-21)
En este fórmulaDmáx es el diámetro exterior máximo medido en cualquier dirección de la misma sección transversal del tubo después de la flexión, y Dmín es el diámetro exterior mínimo medido en cualquier dirección de la misma sección transversal del tubo después de la flexión.
La figura 6-25 es un gráfico de elipticidad, que representa el cambio de elipticidad correspondiente a la curvatura adimensional R0/R (R0 es el radio exterior de la tubería, R es el radio de curvatura de la capa central de la sección de flexión) en una coordenada logarítmica, representada como una familia de rectas con la relación t/R0 como variable parámetro.
Como puede verse en la figura, cuanto mayor es el grado de flexión, mayor es la elipticidad de la sección transversal.
Por lo tanto, la elipticidad se utiliza a menudo en la producción como un índice importante para inspeccionar la calidad de los tubos curvados. En función de las diferentes prestaciones de uso de los materiales de los tubos curvados, también varían los requisitos de su elipticidad.
Por ejemplo, para los componentes de tuberías curvadas utilizados en proyectos de tuberías industriales, la tubería de alta presión no supera los 5%; las tuberías de media y baja presión son de 8%; las tuberías de aluminio son de 9%; y las tuberías de aleación de cobre y aleación de aluminio son de 8%.

La distorsión de la forma de la sección puede reducir el área transversal, aumentando la resistencia al flujo de fluidos, y también puede afectar al rendimiento funcional de la tubería en la estructura.
Por lo tanto, en el proceso de curvado del tubo deben tomarse medidas para controlar la distorsión dentro del rango requerido.
Los métodos eficaces para evitar la distorsión de la forma transversal son:
1) Apoyar la sección transversal con un mandril en la zona de deformación por flexión para evitar la distorsión de la sección transversal.
Para los distintos procesos de curvado, deben utilizarse diferentes tipos de mandriles. Los mandriles rígidos se utilizan a menudo en plegado y bobinado, y la cabeza del mandril tiene forma semiesférica u otra forma de superficie curva.
La Figura 6-26 y la Figura 6-27 permiten determinar si se necesita un mandril durante el plegado y qué tipo de mandril utilizar.

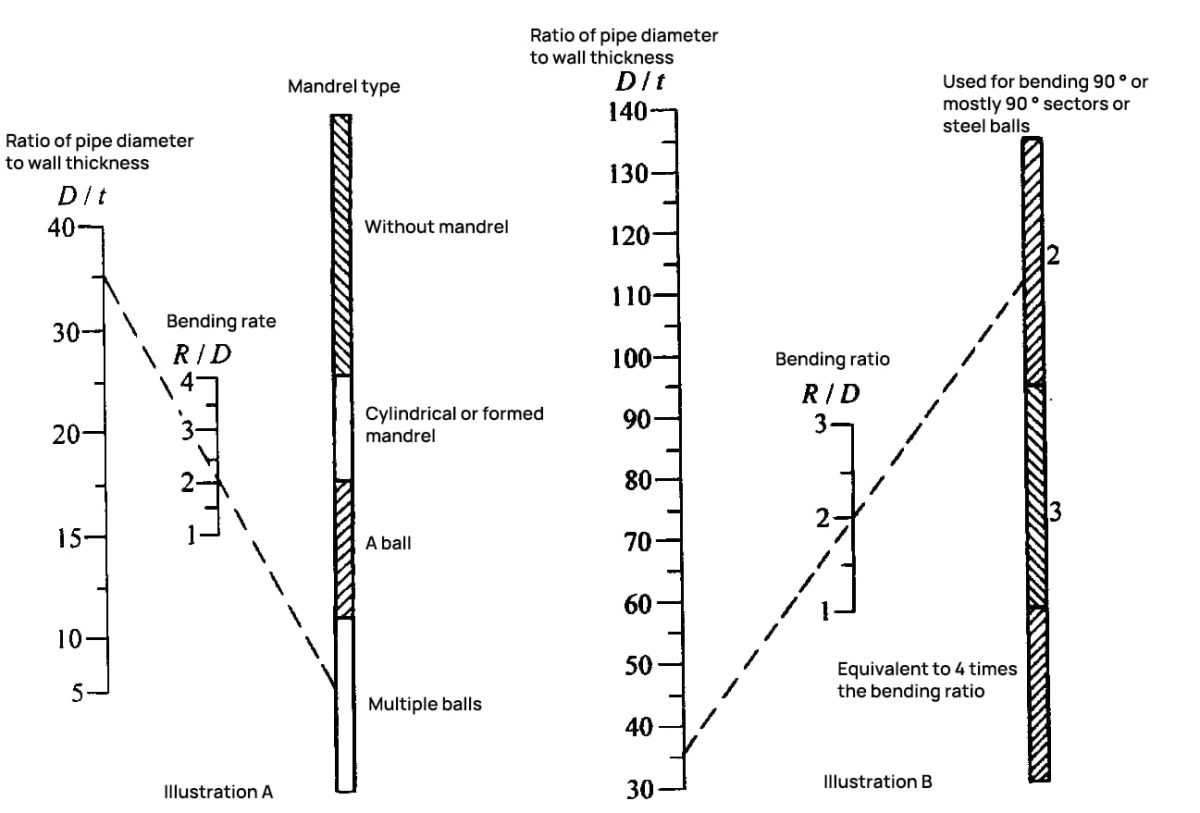
2) Rellenar el tubo doblado con medios granulares, medios fluidos, medios elásticos o aleaciones de bajo punto de fusión también puede sustituir a la varilla central para evitar la distorsión de la forma de la sección. Este método es relativamente fácil de aplicar y se utiliza ampliamente, sobre todo para la producción a pequeña y mediana escala.
3) En la superficie del molde en contacto con el material del tubo, un ranura se hace coincidir con la forma de la sección del material del tubo, reduciendo la presión sobre la superficie de contacto y dificultando la distorsión de la sección. Se trata de una medida bastante eficaz para evitar la distorsión de la forma de la sección.
4) El método de utilizar el método de contra deformación para controlar el cambio en la sección del tubo (Figura 6-28) se utiliza a menudo en el proceso de doblado sin núcleo en el curvatubos. La característica de este método es su estructura sencilla, por lo que su uso está muy extendido.
El uso de la contra deformación para el curvado sin núcleo significa que el tubo en bruto recibe una cierta cantidad de deformación inversa por adelantado. A continuación, tras el curvado, la deformación en diferentes direcciones se anula mutuamente, manteniendo básicamente la sección circular del tubo en bruto para cumplir los requisitos de elipticidad, garantizando así la calidad del tubo curvado.

1-Molde de plegado
2-Bloque de sujeción
3 Rodillos
Rueda de 4 guías
5 tubos ciegos
La forma de la sección transversal de la ranura antideformación se muestra en la Figura 6-29, el tamaño de la ranura antideformación está relacionado con el radio de curvatura relativo (el radio de curvatura de la capa central, el diámetro exterior de la tubería). Véase la tabla 6-4.
Tabla 6-4 Dimensiones de la ranura antideformación
| Radio de curvatura relativo R/D | R1 | R2 | R3 | H |
| 1.5~2 | 0.5D | 0.95D | 0.37D | 0.56D |
| >2~3.5 | 0.5D | 1.0D | 0.4D | 0.545D |
| ≥3.5 | 0.5D | - | 0.5D | 0.5D |

1-Molde de plegado
2-Rodillo antideformación
La variación del grosor del tubo depende principalmente del radio de curvatura relativo R/D y del grosor relativo t/D. En producción, el grosor mínimo de pared tmin en el exterior de flexión y el espesor máximo de pared tmax en el interior puede estimarse normalmente mediante la siguiente fórmula:

En la fórmula,
El adelgazamiento del material del tubo reduce la resistencia mecánica y la facilidad de uso de los racores. Por lo tanto, en la producción, la tasa de adelgazamiento de la pared se utiliza a menudo como un índice técnico para medir el cambio en el espesor de la pared con el fin de cumplir con la usabilidad de los accesorios.
Velocidad de adelgazamiento de la pared del tubo = t-tmin/t×100%
En la fórmula:
El rendimiento de los materiales de las tuberías varía, y existen diferentes requisitos para el índice de reducción del espesor de pared.
Por ejemplo, para los accesorios de tubería utilizados en la ingeniería de tuberías industriales, la tubería de alta presión no supera 10%; la tubería de media y baja presión no supera 15%, y no es inferior al espesor de pared calculado de diseño.
Entre las medidas para reducir el adelgazamiento del espesor de las tuberías se incluyen:
1) Reducir el valor numérico de la tensión de tracción generada en el exterior de la capa neutra. Por ejemplo, utilizando el método de calentamiento local por resistencia para reducir la resistencia a la deformación de la material metálico dentro de la capa neutra, haciendo que la deformación se concentre más en la parte comprimida, logrando el propósito de reducir el nivel de tensión de la parte tensada.
2) Cambiar el estado de tensión de la zona de deformación y aumentar el componente de tensión de compresión. Por ejemplo, cambiar de flexión a empuje puede superar fundamentalmente el defecto de adelgazamiento excesivo de la pared de la tubería.
El cálculo del par de flexión del material del tubo es la base para determinar los parámetros energéticos de la dobladora de tubos.
De acuerdo con el análisis de la teoría de la mecánica plástica, la expresión teórica del momento flector cuando el material de la tubería se dobla uniformemente se deduce como sigue:
Par de flexión del material de la tubería:
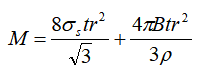
En la fórmula:
El momento de flexión real del material del tubo no sólo depende de las propiedades del material del tubo, la forma y el tamaño de la sección transversal, el radio de flexión y otros parámetros, sino que también está muy relacionado con el método de flexión y la estructura del molde utilizado.
Por lo tanto, actualmente es imposible representar todos estos factores con una fórmula de cálculo, y sólo pueden hacerse estimaciones en la producción.
El par de flexión del material del tubo puede estimarse con la siguiente fórmula:

En la ecuación,
El coeficiente µ no es el coeficiente de fricción; su valor depende del estado de la superficie del tubo, del método de curvado, especialmente si se utiliza un mandril, del tipo y la forma del mandril, e incluso de diversos factores relacionados con la posición del mandril.
En general, cuando se utiliza un mandril rígido sin lubricación, se puede tomar un valor de 5 a 8; cuando se utiliza un mandril rígido articulado, se puede tomar un valor de µ=3.
La forma transversal de la ranura antideformación se muestra en la Figura 6-29.
Las dimensiones de la ranura antideformación están relacionadas con el radio de curvatura relativo (el radio de curvatura de la capa central, el diámetro exterior del tubo).
Véase el cuadro 6-4.
Tabla 6-4 Dimensiones de la ranura antideformación
| Radio de curvatura relativo R/D | R1 | R2 | R3 | H |
| 1.5~2 | 0.5D | 0.95D | 0.37D | 0.56D |
| >2~3.5 | 0.5D | 1.0D | 0.4D | 0.545D |
| ≥3.5 | 0.5D | - | 0.5D | 0.5D |

1-Molde de plegado
2-Rodillo antideformación
La variación del espesor del tubo depende principalmente del radio de curvatura relativo R/D y del espesor relativo t/D.
En producción, el grosor mínimo de pared tmin en el lado exterior de la curva y el espesor máximo de la pared tmax en el lado interior puede estimarse generalmente mediante la siguiente fórmula:

En la fórmula:
El adelgazamiento del material del tubo reduce la resistencia mecánica y el rendimiento de los accesorios de tubería. Por lo tanto, la tasa de adelgazamiento se utiliza a menudo en la producción como un indicador técnico para medir el cambio en el espesor de la pared, con el fin de cumplir con los requisitos de rendimiento de los accesorios de tubería.
Velocidad de adelgazamiento de la pared del tubo = (t-tmin)/t×100%
En la fórmula:
Los diferentes rendimientos del material del tubo requieren diferentes índices de adelgazamiento. Por ejemplo, para los accesorios de tubería utilizados en la ingeniería de tuberías industriales, el tubo de alta presión no debe superar los 10%; los tubos de media y baja presión no deben superar los 15% y no deben ser inferiores al espesor de pared de cálculo de diseño.
Entre las medidas para reducir el adelgazamiento del grosor del tubo se incluyen:
1) Reducir el valor numérico de la tensión de tracción generada en el lado exterior de la capa neutra, como adoptar el método de calentamiento local por resistencia, reduciendo la resistencia a la deformación del material metálico en el lado interior de la capa neutra, haciendo que la deformación se concentre más en la parte comprimida, logrando así el propósito de reducir el nivel de tensión de la parte de tracción.
2) Cambiar el estado de tensión de la zona de deformación y aumentar el componente de tensión de compresión. Por ejemplo, cambiar de flexión a empuje puede superar fundamentalmente el defecto de adelgazamiento excesivo de la pared del tubo.
El cálculo del momento flector del tubo es la base para determinar los parámetros de potencia de la curvadora de tubos. De acuerdo con el análisis de la teoría de la mecánica plástica, la expresión teórica del momento de flexión uniforme del tubo se deriva como sigue:
Par de flexión del tubo:

En la fórmula:
El momento de flexión real del material del tubo no sólo depende del rendimiento del material del tubo, la forma y el tamaño de la sección transversal, el radio de flexión y otros parámetros, sino que también tiene mucho que ver con el método de flexión y la estructura del molde utilizado.
Por lo tanto, actualmente es imposible expresar todos los factores en una fórmula de cálculo, y sólo pueden hacerse estimaciones en la producción.
El momento flector del material del tubo puede estimarse con la siguiente fórmula:

En la fórmula:
El coeficiente no es el coeficiente de fricción µ, su valor depende del estado de la superficie del tubo, del método de curvado, y especialmente si se utiliza un mandril, del tipo y la forma del mandril, e incluso de diversos factores relacionados con la posición del mandril.
En general, cuando se utiliza un mandril rígido sin lubricación, puede tomarse como =5 a 8; si se utiliza un mandril rígido articulado, puede tomarse como µ=3.
La conformación por laminación de tubos es un proceso de conformación especial desarrollado a partir de la conformación tradicional. estampación procesos de rebordeado y cuello. Se trata de un proceso de deformación en el que el borde de la boca del tubo se dobla localmente aplicando presión axial a la pieza tubular a través del molde.
El uso de esta tecnología para fabricar piezas tiene una serie de ventajas, como una tecnología sencilla, menos procesos, bajo coste y buena calidad. Incluso puede producir piezas difíciles de conseguir con otros métodos de estampación.
Este proceso se ha utilizado ampliamente en diversos campos industriales, como el automovilístico y el aeroespacial.
Existen dos formas básicas de conformado de tubos giratorios, a saber, rodillo exterior y rodillo interior (Figura 6-30).

a, b rollo hacia fuera;
c, d balanceo hacia dentro
1-Tubo en blanco
2-Anillo guía de caudal
Molde de 3 conos
Molde de 4 bordes redondeados
Rollo hacia afuera: El tubo en bruto se voltea de dentro a fuera bajo presión axial, aumentando su circunferencia tras el conformado.
Rollo hacia adentro: El tubo en bruto se enrolla de fuera a dentro, reduciendo su circunferencia tras el conformado.
El proceso de laminación no sólo puede formar eficazmente varios tipos de piezas tubulares de doble pared o multicapa, sino también procesar copas de fondo convexo, tubos escalonados, tubos de formas especiales, así como tubos semidobles, cilindros anulares de doble pared, tuercas huecas de doble pared, intercambiadores de calor, silenciadores de automóviles, tubos de guía de ondas en la industria electrónica, etc.
En la actualidad, estas piezas se procesan generalmente mediante estampación en varias fases y métodos de soldaduraque son difíciles, costosas y de escasa calidad estética.
El uso del proceso de laminado garantiza la fiabilidad de la pieza, su ligereza y el ahorro de materias primas.

Actualmente, según los datos, muchos materiales metálicos pueden formarse en el molde con distintos métodos de laminación, como aleación de aluminio, cobre y aleaciones de cobre, acero de bajo contenido en carbono, acero inoxidable austenítico, etc. Las piezas brutas de tubo de todas las especificaciones de sonido pueden laminarse con éxito en tubos de doble capa.
El perfilado, comparado con otros procesos de conformadotiene un proceso de deformación más complejo, que incluye el abocardado, el rizado, el laminado y su conversión mutua.
Existen varios moldes para realizar este proceso de conformado, entre los cuales los más sencillos y utilizados son los moldes cónicos y los moldes de filete.
1. Molde de laminación de tubos cónicos
La estructura del molde de laminación de tubos cónicos se muestra en la Figura 6-32. Este estructura del molde es simple, y se pueden formar diferentes especificaciones de tubos en un solo juego de moldes, lo que es difícil de conseguir en otros moldes de formación de tubos.
Además, como proceso de preformado para el perfilado de tubos de precisión, se utiliza ampliamente el moldeado cónico.

a Estructura del molde abatible
b Parámetros del proceso de volteo de tubos cónicos
1 - Cabezal de prensa
2 - Tubo Billet
3 - Molde cónico
Durante el proceso de torneado de tubos, un extremo del tubo en bruto se coloca en una matriz cónica, mientras que el otro extremo se somete a la presión axial de la corredera de la prensa para lograr el torneado del tubo en bruto.
Al diseñar este tipo de troquelel ángulo de semicono α de la matriz es el parámetro más crítico.
El tamaño de α no sólo determina la viabilidad del torneado de tubos, sino que también afecta a las dimensiones geométricas del torneado de tubos, es decir, al coeficiente de torneado de tubos K(K=D/D1, donde D y D1 son el diámetro exterior de la pieza bruta de tubo y el diámetro exterior del torneado de tubo, respectivamente).
Obviamente, existe un ángulo semicónico crítico α0, y el giro sólo puede realizarse normalmente cuando el ángulo semicónico α≥ α0.
µ, H, Golubnov derivado basado en el principio de la tensión principal:

Teniendo en cuenta la influencia del refuerzo del material y la rigidez del extremo abocinado, la fórmula anterior puede modificarse como sigue:

En la fórmula:

Para un tubo de aluminio 3A21 de 42 mm, calculado mediante la fórmula anterior, el ángulo es de 55° - 60°.
Las pruebas empíricas demuestran que cuando el ángulo es α≥60° (α≈68°), el volteo del tubo puede realizarse sin problemas. En este momento, la presión axial es la más pequeña.
Cuando el ángulo es de 55° - 60°, el extremo del tubo en blanco se riza pero no entra en la fase de volteo. Cuando el ángulo es α<55°, el extremo del tubo sólo se ensancha en la matriz cónica y no se curva.
Durante el volteo de la matriz cónica, el extremo del tubo se desliza con facilidad, lo que provoca que la parte volteada del tubo quede fuera del eje con respecto a la pieza bruta del tubo original y que se produzca una flexión axial durante el volteo.
Es difícil conseguir una pieza de tubo volteado de doble capa que cumpla los requisitos de calidad del montaje. De ahí que sea necesario un redondo Se desarrolló un troquel de volteo de esquinas basado en el troquel cónico.
2. Troquel abatible de esquinas redondeadas
La matriz de volteo de esquina redonda utiliza la parte de trabajo de la matriz, que es un círculo de radio, para forzar el extremo del tubo comprimido axialmente a deformarse a lo largo de su arco para lograr el volteo del tubo.
La figura 6-33 muestra un diagrama esquemático de un tubo en bruto con un espesor de t y un diámetro medio de D, laminado en una matriz de esquina redonda con un radio de r, bajo carga axial, el extremo del tubo se curva hacia arriba a lo largo del arco de la matriz para obtener una pieza de tubo laminado con un diámetro de D1.
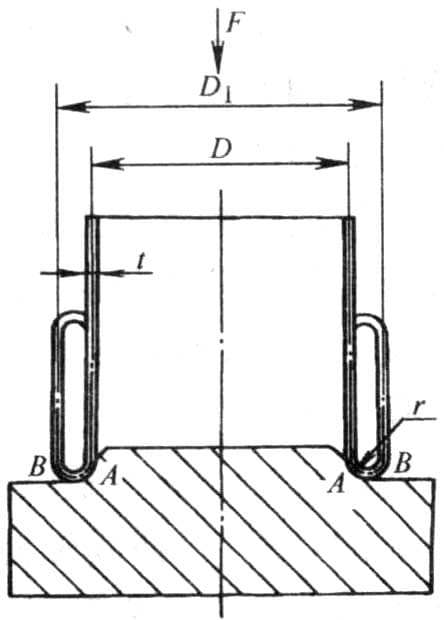
El parámetro más importante en el diseño de una matriz de rebordeado de esquina redonda es el radio r de la esquina de la matriz. No solo determina las dimensiones geométricas de la pieza rebordeada, sino que también influye en la magnitud de la fuerza de rebordeado.
Para el 3A21 recocido tubo de aluminio de tipo Φ41×1, tanto el análisis teórico como los resultados experimentales muestran que el radio crítico del fileteado de la matriz (radio mínimo del fileteado) para la inestabilidad de la inversión del tubo es de unos 2 mm; el radio óptimo del fileteado es de aproximadamente 3 mm; el radio máximo del fileteado es de unos 4 mm.
Esto indica que la estabilidad y la calidad de la inversión del tubo bajo carga axial dependen del radio r del filete de la matriz. Si r es inferior a un determinado valor crítico, el extremo del tubo no se curva a lo largo del arco de la matriz; cuando r es demasiado grande, el extremo del tubo se fractura y no puede invertirse con éxito. Sólo cuando r se encuentra dentro de un rango adecuado puede realizarse la inversión del tubo.
De forma similar al curvado hacia fuera del material del tubo, el curvado hacia dentro del tubo también puede llevarse a cabo en el molde cónico y en el molde de filete (Figura 6-34).
En comparación con otros procesos de conformado, es propenso a la inestabilidad. Debido a que durante el curvado hacia el interior, el diámetro del tubo disminuye después de la deformación, la pared del tubo se espesa, la fuerza de inversión del tubo aumenta, lo que trae dificultades a la formación de curvado.
Según los cálculos teóricos y la práctica, cuando el ángulo semicónico crítico β del molde cónico de inversión del tubo es ≥120°, el proceso de rizado puede desarrollarse sin problemas. En la producción, el valor suele tomarse como β≥120°~125°, rp≈4mm.
El proceso de curvado del tubo sólo puede producirse cuando la carga necesaria para el curvado es inferior al límite de inestabilidad axial. Dado que la carga de formación del curvado depende en gran medida de los parámetros geométricos del molde, en términos del molde de filete, depende del radio de filete r.
Por lo tanto, se puede determinar una región factible para la formación de rizos (Figura 6-35).

un troquel cónico
b Dado redondeado

De la Figura 6-35, se puede ver que el área de laminación interna es bastante pequeña, y la carga de laminación es numéricamente mayor que la de laminación externa, llegando casi a 50%.
Los datos existentes muestran que, tanto a nivel nacional como internacional, se han estudiado teórica y prácticamente los parámetros óptimos del proceso de laminado exterior, y se ha descubierto la relación entre el esfuerzo de compresión axial mínimo necesario para el laminado completo y el diámetro interior, el diámetro exterior y el grosor de la pared del material tubular.
Durante el laminado exterior de materiales tubulares, el cambio del grosor de la pared no es significativo.
Sin embargo, durante la laminación interna, el esfuerzo de compresión circunferencial hace que el espesor de la pared en el filete del molde aumente continuamente hasta alcanzar un valor constante, que puede ser 1,5 veces el espesor original. Por lo tanto, para completar su laminación interna, se requiere una carga axial mayor.
En los dos tipos de laminado antes mencionados (laminado tradicional), existen algunas deficiencias:
1. El comienzo de la segunda capa de la pared del tubo no es paralelo a la pared original del tubo, sino que gira siempre hacia la cavidad interior del tubo de doble pared;
2. Existe una cierta distancia entre la pared del tubo nuevo y la pared del tubo original, que depende del diámetro relativo (D/t) del material del tubo original;
3. En el laminado interior, la segunda capa de la pared del tubo es considerablemente más gruesa, lo que a su vez provoca un aumento de la presión axial durante el laminado.
Los problemas que surgen en los procesos mencionados se deben al mecanismo de conformado, que limita la forma geométrica de los tubos obtenidos, especialmente la escasa estabilidad y la elevada dificultad del proceso de laminación interna, que es necesario mejorar.
Por lo tanto, ha surgido el método de conformado por laminación con esfuerzo de tracción para la laminación interna de materiales tubulares.
La característica del método de conformación por laminación con esfuerzo de tracción es que detiene la laminación en la primera etapa de laminación interna del material tubular, y da al borde laminado una curvatura inversa, dirigiéndolo hacia el exterior de la cavidad.
Entonces, por la acción del molde convexo, la fuerza de tracción que actúa sobre el borde de curvatura inversa en la pared interior hace que la pieza bruta de tubo sufra un enrollamiento interno, en lugar de enrollarse por la presión axial que actúa sobre la pared exterior, reduciendo así su presión axial.
Este proceso puede lograr una mayor altura de la pared interior, un grosor de pared constante y una mayor precisión del producto.
El método de perfilado por tensión de tracción ha ampliado el rango de aplicación del proceso de perfilado interno, como la producción de juntas de tuberías, asientos de rodamientos y otros (Figura 6-36).

El método de perfilado por tracción puede dividirse en tres pasos, como se muestra en la figura 6-37.
En el primer paso (Figura 6-37a), el laminado interior tradicional termina cuando el borde del tubo sale de una cuarta parte de la matriz de fileteado.
En este momento, la distancia entre el borde del tubo y la pared interior de la matriz formará el soporte radial del producto final y debe ser igual a la anchura requerida.
En el segundo paso (Figura 6-37b), la matriz convexa de fondo plano desciende, forzando el rebordeado del borde del tubo (similar a la rebordeado de agujeros de la placa). La separación entre la matriz convexa y la matriz del rodillo interior viene determinada por el grosor de la pared del tubo (el grosor de la pared del rodillo interior del tubo aumenta ligeramente).
En el tercer paso (Figura 6-37c, d), la matriz convexa de formación se eleva, haciendo que el borde del tubo ruede hacia dentro, generando así la segunda capa de pared del tubo bajo el empuje de la matriz convexa de formación.
Como puede observarse en la figura, la matriz convexa de conformación actúa sobre el borde del tubo con esfuerzos de tracción y no de compresión que actúan sobre todo el tubo.
No hay deslizamiento relativo entre la matriz y el material deformado, y se mantiene una distancia entre las cargas de conformación, con lo que se reduce la tensión axial de compresión en la zona de transmisión del tubo, evitando así la inestabilidad.
Por lo tanto, el laminado por tracción tiene mayor libertad a la hora de elegir el radio de laminación, mientras que el radio de la matriz es un parámetro de proceso importante en los procesos de mecanizado tradicionales (Figura 6-35).

Condiciones para la correcta ejecución de este proceso:
FPerforación≥FRodando (6-22)
La fuerza de punzonado incluye tres componentes (símbolo de la figura 6-37d): la carga que provoca la deformación plástica del material en el radio rP; la carga necesaria para superar la fricción en la esquina ra entre el punzón y el borde del tubo; la carga necesaria para doblar y desdoblar el material del borde desde la posición radial a la axial.
En la expresión analítica, σ1 se utiliza para representar la tensión de deformación interna de la pared.
Entonces,

La conformación por laminación incluye dos aspectos: la carga necesaria para la laminación del material en diferentes posiciones de radio de curvatura y la carga necesaria para la flexión y el rebote desde el principio hasta el final de la zona de deformación.
En el análisis, σ0 se utiliza para representar la tensión de deformación de la pared exterior, y σm representa la tensión media de deformación plástica en la zona de deformación.

Conclusión:
El método de conformación del tubo mediante laminado sometido a tracción se ha demostrado mediante experimentos.
Aunque se requieren dos etapas de preparación antes del inicio de la laminación y se precisa un recocido de recristalización cuando es necesario, presenta las siguientes ventajas en comparación con el proceso de laminación tradicional:
1) El borde laminado gira hacia el centro de la cavidad, lo que facilita la coordinación con otras piezas, como la bola rodamiento asientos.
2) La carga de rodadura se reduce considerablemente.
3) El límite de conformado se mejora considerablemente, y los productos con un radio de laminación menor puede obtenerse.
4) No hay fricción ni necesidad de lubricación.
5) El espesor de la pared interior es aproximadamente igual al de la pared exterior, y sólo el borde sometido a carga es ligeramente más grueso (figura 6-38).
Las condiciones experimentales de la pieza mostrada en la Figura 6-38 son las siguientes:
El tubo es de acero de bajo contenido en carbono, Dfuera = 90 mm, t0= 2,4 mm, H =150 mm.
El diámetro de la matriz cóncava (figura 6-37d) es Dd = 97 mm.
El diámetro de la matriz convexa (Figura 6-37d) es Dp =72mm.
6) Debido a la ausencia de fricción y a la doble coacción de las matrices convexa y cóncava sobre la pared de la pieza, ésta presenta una gran precisión dimensional (figura 6-37d).
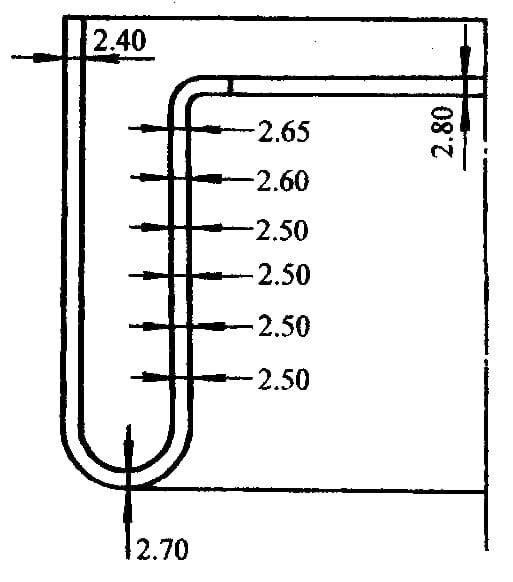
Figura 6-37 Proceso de perfilado por tracción (Proceso de perfilado interior mejorado)
Condiciones para el éxito de la aplicación de este proceso:
FPerforación≥FRodando (6-22)
En fuerza de perforación incluye tres elementos (símbolo de la figura 6-37d): la carga que provoca la deformación plástica del material en el radio rp; la carga necesaria para superar la fuerza de fricción entre la esquina del punzón en ra y el borde del tubo; la carga necesaria para la flexión y la flexión inversa del material del borde desde la posición radial a la axial.
En la expresión analítica, σ1 representa la tensión de deformación de la pared interior.

El perfilado incluye dos aspectos: la carga necesaria para que el material ruede hasta diferentes posiciones de radio (curvatura) y la carga necesaria para el doblado y el doblado inverso desde el principio hasta el final de la zona de deformación.
En el análisis, σ0 se utiliza para representar la tensión de deformación de la pared exterior, y σm se utiliza para representar la tensión media de deformación plástica en la zona de deformación.

Conclusión:
El método de conformación de materiales de tuberías mediante laminado por tracción ha sido probado mediante experimentos. Aunque son necesarias dos etapas de preparación antes de iniciar la laminación y el recocido de recristalización cuando es necesario, presenta las siguientes ventajas sobre los procesos de laminación tradicionales:
1) El borde laminado gira hacia el centro de la cavidad, lo que facilita la cooperación con otras piezas, como los asientos de los rodamientos de bolas.
2) La carga de rodadura se reduce considerablemente.
3) El límite de conformado mejora considerablemente, y los productos con radios de laminación más pequeños puede obtenerse.
4) No hay fricción ni necesidad de lubricación.
5) El espesor de la pared interior es aproximadamente igual al de la pared exterior, y sólo los bordes sometidos a carga son ligeramente más gruesos (figura 6-38).
Las condiciones experimentales de las piezas mostradas en la Figura 6-38 son las siguientes:
El material de la tubería es acero con bajo contenido en carbono, Dfuera = 90 mm, t0 = 2,4 mm, y el radio H es de 150 mm.
El diámetro de la matriz Dd (Figura 6-37d) es de 97 mm.
El diámetro del punzón (Figura 6-37d) es Dp =72mm.
6) Debido a la ausencia de fricción y a la doble coacción del punzón y la matriz sobre la pared de la pieza, ésta presenta una mayor precisión dimensional (Figura 6-37d).