¿Alguna vez se ha preguntado por qué algunos materiales se doblan con facilidad y otros permanecen rígidos? Este blog se sumerge en el fascinante mundo del módulo elástico y la rigidez, desentrañando sus funciones cruciales en ingeniería. Al final, entenderás cómo influyen estas propiedades en la resistencia y flexibilidad de los materiales cotidianos.
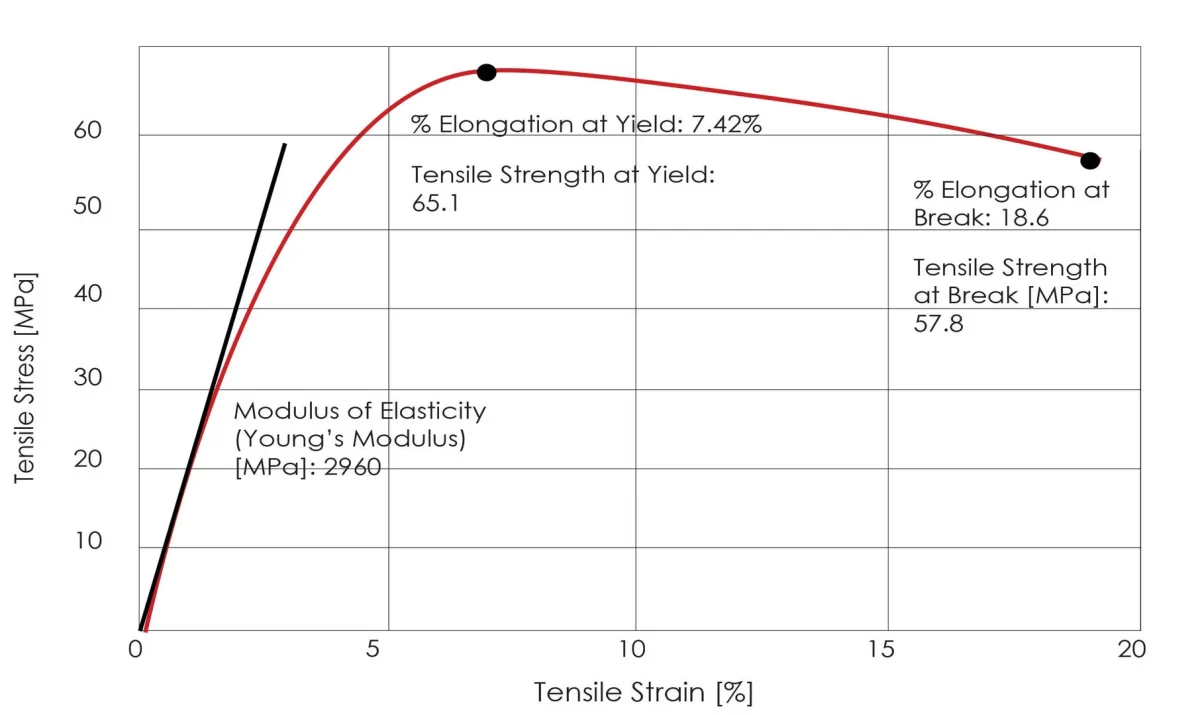
Módulo de elasticidad: Relación entre la tensión normal y la deformación normal correspondiente en la fase de deformación elástica de un material.
En la fase de deformación elástica, la tensión y la deformación de un material son proporcionales, de acuerdo con la Ley de Hooke, y el coeficiente de proporcionalidad se denomina módulo elástico.
El término "módulo de elasticidad" es una descripción general de la elasticidad de un material. Abarca varios módulos específicos, como el módulo de Young, el módulo de cizallamiento y el módulo de masa, entre otros.
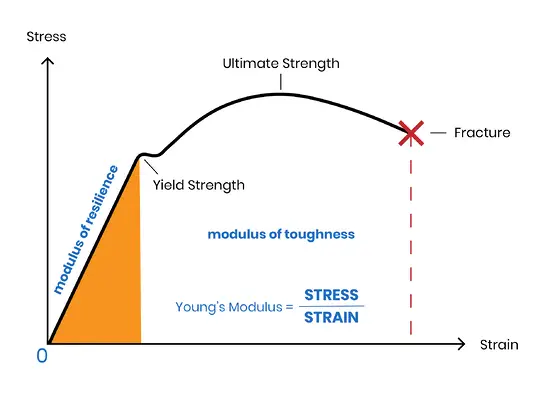
Por lo tanto, "módulo elástico" y "módulo aparente" son términos inclusivos.
Cuando se aplica una fuerza externa (denominada "tensión") a un elastómero, éste cambia su forma (denominada "deformación"). El módulo elástico se define como la relación entre la tensión y la deformación.
Por ejemplo:
Tensión lineal:
Cuando se aplica una fuerza de tracción F a una varilla delgada, la tensión lineal se calcula como la fuerza de tracción dividida por el área de la sección transversal S de la varilla.
La deformación lineal se calcula como el alargamiento de la varilla (dL) dividido por su longitud original (L).
La tensión lineal dividida por la deformación lineal es igual al módulo de Young, E = (F / S) / (dL / L).
Tensión de cizallamiento:
Cuando se aplica una fuerza lateral (normalmente una fuerza de fricción) f a un elastómero, éste cambia de forma cuadrada a forma de diamante.
Este ángulo de deformación se conoce como "deformación por cizalladura", y la fuerza correspondiente dividida por el área de tensión se denomina "tensión por cizalladura".
El esfuerzo cortante dividido por la deformación cortante es igual al módulo cortante, G = (f / S) / a.
Tensión de volumen:
Cuando se aplica una presión global P al elastómero, se conoce como "tensión de volumen".
La reducción del volumen del elastómero (-dV) dividida por su volumen original (V) se denomina "deformación volumétrica".
La tensión volumétrica dividida por la deformación volumétrica es igual al módulo aparente, K = P / (-dV / V).
En general, cuando no hay confusión, el módulo elástico de los materiales metálicos se refiere al módulo de Young, también conocido como módulo elástico positivo.
Unidad: E (módulo de elasticidad) se mide en GPa.
El módulo elástico es un parámetro crucial del rendimiento de los materiales de ingeniería.
Desde una perspectiva macro, mide la capacidad de un objeto para resistir la deformación elástica, mientras que desde un punto de vista micro, refleja la fuerza de unión entre átomos, iones o moléculas.
Los factores que afectan a la resistencia de la unión también pueden influir en el módulo elástico de un material, como el modo de unión, la estructura cristalina, la composición química, la microestructura y la temperatura, entre otros.
El módulo de Young de materiales metálicos puede fluctuar en más de 5% debido a las diferentes composiciones de aleación, estados de tratamiento térmico y deformaciones plásticas en frío.
Sin embargo, en términos generales, el módulo elástico de materiales metálicos es un índice de propiedades mecánicas insensible a la estructura.
La aleación, el tratamiento térmico (estructura de la fibra) y la deformación plástica en frío tienen un efecto limitado sobre el módulo elástico, y los factores externos como la temperatura y la velocidad de carga tienen un impacto insignificante sobre él.
Por lo tanto, en las aplicaciones generales de ingeniería, el módulo elástico se considera una constante.
Unidad: GPa (gigapascales) para el módulo elástico.
El módulo elástico es una medida de la resistencia de un material a la deformación elástica.
Cuanto mayor sea su valor, mayor será la tensión necesaria para producir una determinada deformación elástica, lo que significa que el material es más rígido y experimenta menos deformación elástica bajo una tensión dada.
El módulo elástico, representado por E, es una medida de la cantidad de tensión necesaria para que un material sufra una deformación elástica unitaria bajo una fuerza externa.
Representa la capacidad del material para resistir la deformación elástica y puede compararse con la rigidez de un resorte.
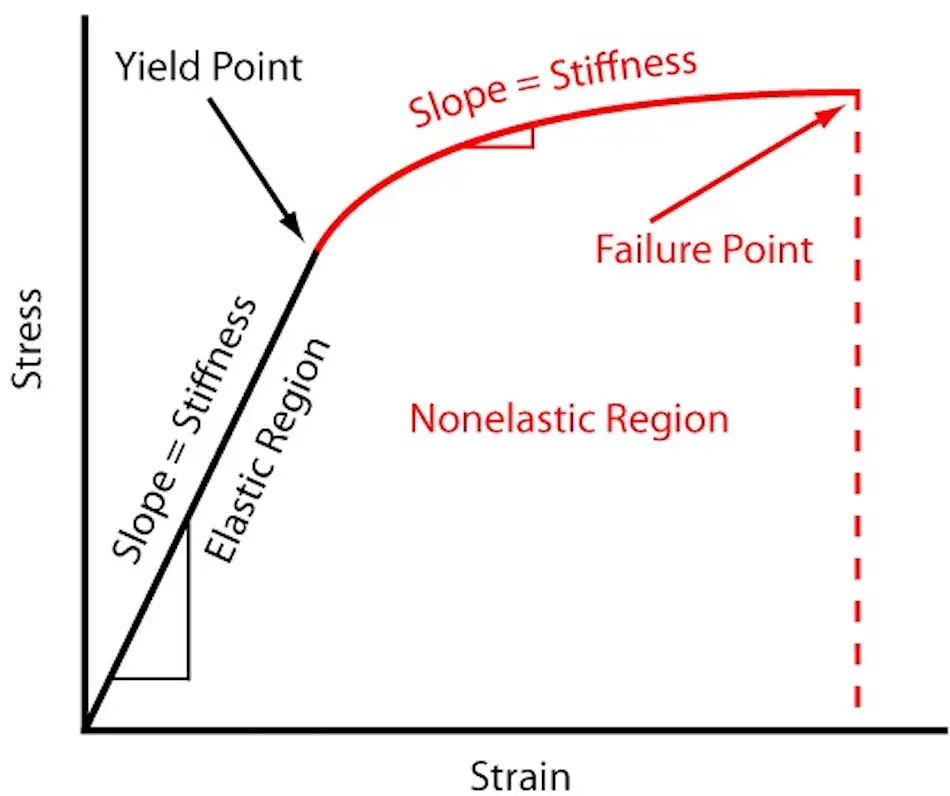
La "rigidez" se refiere a la capacidad de una estructura o componente para resistir la deformación elástica. Viene determinada por la fuerza o el momento necesarios para producir una unidad de deformación.
En términos de rigidez rotacional, se representa por "k" y se puede calcular como "k = M / θ", donde "M" es el par aplicado y "θ" es el ángulo de rotación.
Otras rigideces son:
El método de cálculo de la rigidez puede dividirse en dos enfoques: la teoría del pequeño desplazamiento y la teoría del gran desplazamiento.
La teoría de grandes desplazamientos tiene en cuenta la deformación de la estructura tras el esfuerzo y forma la ecuación de equilibrio en consecuencia, proporcionando resultados precisos pero con un proceso de cálculo más complejo.
Por el contrario, la teoría de los pequeños desplazamientos supone que la estructura no se deforma significativamente, por lo que la fuerza interna puede obtenerse a partir de la carga externa y utilizarse después para calcular la deformación.
Este enfoque se utiliza ampliamente en la mayoría de las aplicaciones de diseño mecánico, ya que es mucho más sencillo de resolver.
Por ejemplo, en el cálculo de la deformación por flexión de una viga, se suele emplear la teoría del pequeño desplazamiento porque la deformación real es muy pequeña.
Esta teoría implica ignorar la primera derivada de la deflexión en la fórmula de curvatura y utilizar la segunda derivada de la deflexión para aproximar la curvatura del eje de la viga, lo que ayuda a simplificar el proceso de solución al linealizar la ecuación diferencial.
Cuando actúan varias cargas simultáneamente, la deformación por flexión causada por cada carga puede calcularse por separado y luego combinarse.
La resistencia a la deformación bajo una carga estática se conoce como rigidez estática, mientras que la resistencia a la deformación bajo una carga dinámica se denomina rigidez dinámica, es decir, la cantidad de fuerza dinámica necesaria para una amplitud unitaria.
Cuando la fuerza interferente cambia lentamente (es decir, la frecuencia de la fuerza interferente es mucho menor que el frecuencia natural de la estructura), la rigidez dinámica es esencialmente igual a la rigidez estática.
Sin embargo, si la fuerza interferente cambia rápidamente (es decir, la frecuencia de la fuerza interferente es mucho mayor que la frecuencia natural de la estructura), la deformación estructural será relativamente pequeña y, por tanto, la rigidez dinámica será relativamente grande.
Si la frecuencia de la fuerza interferente se aproxima a la frecuencia natural de la estructura, se produce la resonancia, y la rigidez dinámica estará en su mínimo, lo que hará que la estructura sea la más fácil de deformar, con su deformación dinámica capaz de alcanzar varias veces o incluso más de diez veces la de la deformación de la carga estática.
Una deformación excesiva de los componentes puede afectar a su funcionamiento.
Por ejemplo, la deformación excesiva de un eje de engranaje puede afectar al engranaje, y la deformación excesiva de una máquina herramienta puede reducir la precisión del mecanizado.
Los factores que afectan a la rigidez son el módulo elástico de los materiales y la forma estructural. Cambiar la forma estructural puede tener un impacto significativo en la rigidez.
El cálculo de la rigidez es la base de la teoría de las vibraciones y el análisis de la estabilidad estructural. Cuando la masa permanece constante, una rigidez elevada se traduce en una frecuencia natural alta.
La distribución de tensiones en una estructura estáticamente indeterminada está relacionada con la relación de rigidez de cada parte.
En mecánica de fractura el factor de intensidad de la tensión de un elemento agrietado puede determinarse en función de su flexibilidad.
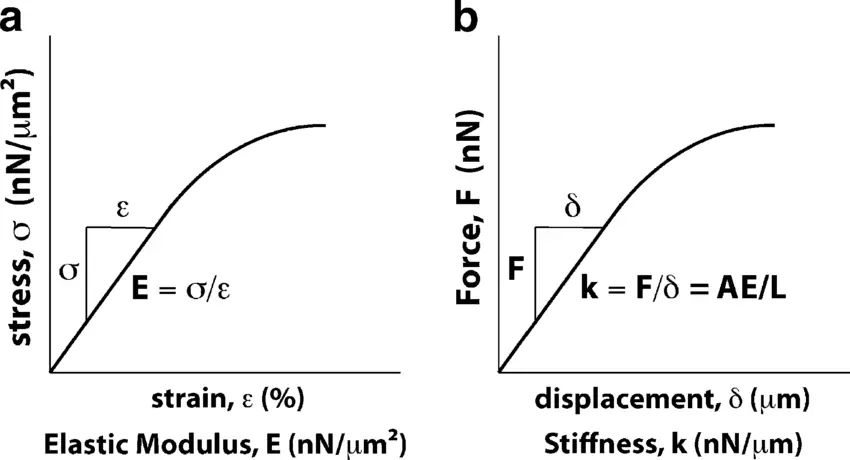
La rigidez y el módulo elástico son conceptos fundamentales en la ciencia de los materiales, cada uno de los cuales describe aspectos diferentes de la resistencia de un material a la deformación. Aunque están relacionados, desempeñan funciones distintas en el análisis y la aplicación de materiales.
El módulo elástico, también conocido como módulo de Young, es una medida específica de la capacidad inherente de un material para resistir la deformación bajo tensión. Cuantifica la relación entre la tensión (fuerza por unidad de superficie) y la deformación (deformación proporcional) en la región elástica lineal de la curva tensión-deformación del material. El módulo elástico es una propiedad del material e independiente de su forma o tamaño. Se expresa en unidades de presión, como los pascales (Pa).
La rigidez, por su parte, es un término más amplio que se refiere a la resistencia de una estructura a la deformación elástica bajo una carga aplicada. No es sólo una propiedad de los materiales, sino que también depende de la geometría y las condiciones de contorno de la estructura. La rigidez suele expresarse como la fuerza necesaria para lograr un desplazamiento unitario (por ejemplo, newtons por metro, N/m).
La rigidez de un elemento estructural puede obtenerse a partir del módulo elástico del material y de la geometría del elemento. Por ejemplo, la rigidez a flexión (EI) de una viga es el producto del módulo elástico (E) y el momento de inercia (I) de la sección transversal de la viga. Del mismo modo, la rigidez torsional (GI) es el producto del módulo de cizalladura (G) y el momento polar de inercia (I).
La rigidez es crucial en el diseño de ingeniería, sobre todo para componentes que deben mantener su forma bajo carga, como husillos, raíles guía y husillos de rosca. También es esencial para las estructuras que requieren un estricto control de la deformación, como las alas de los aviones y los ensamblajes de alta precisión.
La resistencia es la capacidad de un material para resistir la deformación permanente y la fractura bajo fuerzas externas. Abarca varios tipos de resistencia, como el límite elástico, la resistencia a la tracción, la resistencia a la compresión y la resistencia a la flexión. Estas propiedades son fundamentales para determinar la capacidad de carga y la durabilidad de las piezas mecánicas.
Comprender la diferencia entre rigidez y módulo elástico es esencial para diseñar y analizar componentes y estructuras mecánicas. Mientras que el módulo elástico proporciona una medida de la resistencia intrínseca de un material a la deformación, la rigidez tiene en cuenta tanto las propiedades del material como los factores geométricos para describir la resistencia global de una estructura a la deformación. Ambos conceptos son esenciales para garantizar el rendimiento y la fiabilidad de los diseños de ingeniería.
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
DE 
FR 
IT 
NL 
PT 
RU 