Medición de la Rectitud: Cómo calcular como un profesional

1. Introducción

En la práctica de la ingeniería, existen dos métodos comúnmente utilizados para evaluar el error de rectitud de los carriles guía: el método de conexión de dos puntos extremos y el método de la condición mínima.

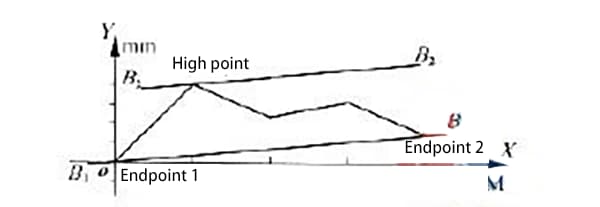
El método de conexión de dos puntos extremos conecta la curva de error de extremo a extremo, luego traza dos líneas paralelas a la línea de extremo a extremo en los puntos más alto y más bajo de la curva, y mide los valores a lo largo del eje vertical entre las dos líneas paralelas.

Tras el procesamiento de los datos, el valor es el error de rectitud del carril guía.

El método de la condición mínima conecta los puntos "alto, alto" (o "bajo, bajo") de la curva de error y traza una línea paralela que pasa por el punto bajo (alto).

El valor medido entre las dos líneas paralelas a lo largo del eje vertical es el error de rectitud del carril guía tras el procesamiento de los datos.

El método de la condición mínima es una evaluación de arbitraje.

El método de conexión de dos puntos finales no es una evaluación de arbitraje, pero se utiliza comúnmente en producción debido a su simplicidad y comodidad en la evaluación, aunque a veces puede producir grandes errores.

Este artículo analiza el valor límite del error generado entre estos dos métodos de evaluación.

2. La curva de error está en el mismo lado que ambos extremos de la línea

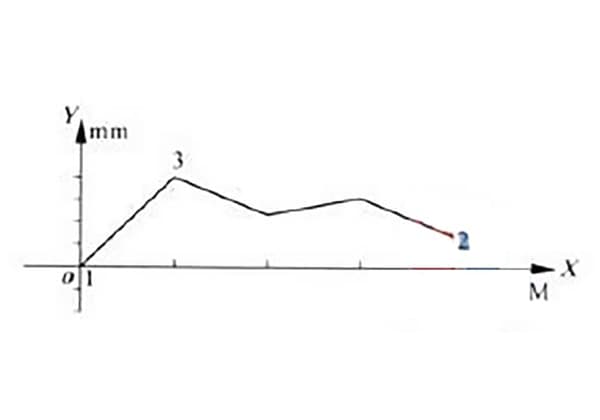
Midiendo el error de rectitud de un cierto modelo de guía de riel de deslizamiento hidráulico, la curva de error de rectitud se obtuvo como se muestra en la Figura 1.

Como puede verse en la figura, la curva de error está en el mismo lado que ambos extremos de la línea.

A continuación, se evaluará el valor del error de rectitud del carril guía utilizando el método de la condición mínima y el método de conexión de dos extremos.

(1) Evaluación del error de rectitud mediante el método de la condición mínima

Según el método de la condición mínima, los puntos más bajos 1 y 2 de la curva de la figura 1 (con el punto más bajo 1 coincidiendo con el origen) están conectados por la línea a1a1, tal como se muestra en la figura 2.

Se traza la recta paralela a2a2 por el punto más alto 3 respecto a la recta a1a1.

El valor medido a lo largo del eje y en la región delimitada por las dos líneas paralelas a1a1 y a2a2, una vez procesados los datos, representa el error de rectitud del carril guía δ obtenido a partir del método de la condición mínima.

(2) Evaluación del error de rectitud mediante el método de conexión de dos extremos

Según el método de conexión de dos extremos, los extremos de la curva de la figura 1 son también los puntos extremos 1 y 2 de la curva, como se muestra en la figura 3.

Los puntos extremos 1 y 2 se unen mediante la recta b1b1, y a continuación se traza una recta paralela b2b2 que pasa por el punto más alto.

El valor medido a lo largo del eje y en la región delimitada por las dos líneas paralelas b1b1 y b2b2, una vez procesados los datos, representa el error de rectitud del carril guía δ obtenido a partir del método de conexión de dos extremos.

(3) Determinación del límite de error generado por los dos métodos de evaluación

Dado que ambos métodos de evaluación se utilizan para determinar el error de rectitud del mismo carril guía, el "punto bajo 1", el "punto bajo 2" y el "punto alto 3" de la figura 2 se corresponden respectivamente con el "punto final 1", el "punto final 2" y el "punto alto 3" de la figura 3. Esto hace que la línea a1a1 coincida con la línea b1b1, y que la línea a2a2 coincida con la línea b2b2.

Por lo tanto, el valor del error generado por los dos métodos de evaluación es cero.

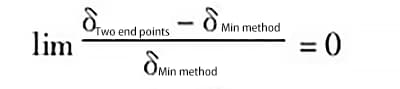
Según el análisis anterior, cuando la curva de error está en el mismo lado que ambos extremos de la línea, el límite de error generado por los dos métodos de evaluación es cero, lo que significa que los resultados de evaluación obtenidos por los dos métodos son los mismos.

3. La curva de error está a ambos lados de la línea que une los extremos

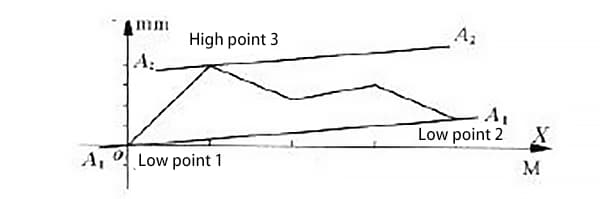
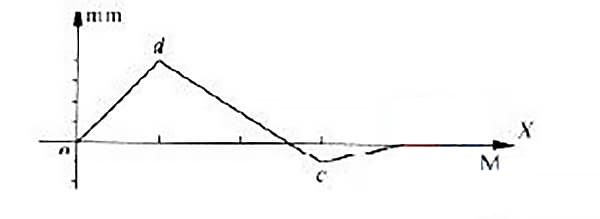
En la curva de error de rectitud medida de un carril guía, algunas curvas de error se encuentran a ambos lados de la línea que une los extremos, como se muestra en la figura 4.

La curva de error de este carril guía tiene una línea que une sus extremos coincidiendo con el eje x. El error de rectitud del carril guía se evaluará utilizando el método de la condición mínima y el método de conexión de dos extremos.

Como puede verse en la figura 4, los puntos o y c son los dos puntos bajos y los dos puntos extremos de la curva, mientras que el punto d es el punto más alto.

Según el método de la condición mínima, los puntos o y c están conectados por la recta a1a1, como se muestra en la figura 5. La recta a2a2 se traza paralela a la recta a1a1 pasando por el punto más alto d.

El valor medido a lo largo del eje y en la región delimitada por las dos líneas paralelas a1a1 y a2a2, una vez procesados los datos, representa el error de rectitud del carril guía δ obtenido a partir del método de la condición mínima.

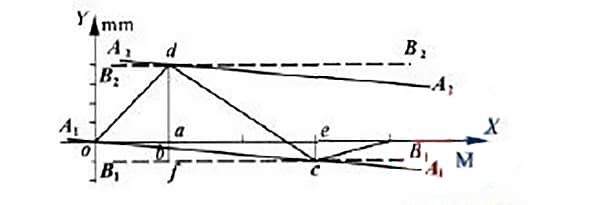
Según el método de conexión de dos puntos, traza dos rectas paralelas al eje x que pasen respectivamente por los puntos C y D.

Estas líneas están representadas por las líneas punteadas b1b1 y b2b2 en la figura 5. En la región delimitada por estas dos líneas paralelas, el valor medido a lo largo del eje y, tras el tratamiento de los datos, representa el valor del error de rectitud del carril de guía entre los dos puntos extremos.

Para determinar el método de la desviación mínima y el valor de la desviación en los dos puntos extremos, trace una línea paralela al eje y que pase por el punto D, intersecte el eje en el punto A, intersecte la línea a1a1 en el punto H e intersecte la línea b1b1 en el punto F.

Análogamente, traza una recta paralela al eje y que pase por el punto C y corte al eje en el punto E.

(1) Determinación del error de rectitud mediante el método de la condición mínima

Según el método de la condición mínima, el valor del error de rectitud δ del carril guía se obtiene a partir del valor medido a lo largo del eje y tras el procesamiento de los datos, lo que representa el método de la desviación mínima.

Como se muestra en la figura 5:

Y como BD = BA + AD,

∆OAB y ∆OEC son dos triángulos semejantes, por lo tanto,

Reordenando la ecuación (3), obtenemos:

Sustituyendo la ecuación (4) en la ecuación (2) y reordenando, obtenemos:

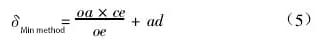
(2) Determinación del error de rectitud mediante el método de conexión de dos puntos

Según el método de conexión de dos puntos, el valor medido a lo largo del eje y tras el procesamiento de los datos representa el valor de error de rectitud δ del carril guía entre los dos puntos extremos.

Como se muestra en la figura 5:

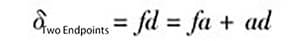
Y como fa = ce,

(3) Cálculo de los valores de error generados por dos métodos de evaluación

Ecuación (6) menos ecuación (5), es decir,

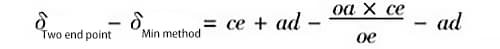
Reordenando, obtenemos:

(4) Cálculo del error máximo generado por dos métodos de evaluación

En la figura 5, sea ad = δ1, ce = δ2, oa = p; sea l la longitud del carril guía que se mide, entonces oe = l - p, y:

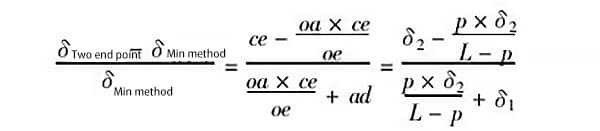
Por ejemplo, cuando p = 0,5m (es decir, el paso es de 0,5m), δ1 = 1,0δ, δ2 = 0,25δ, y la longitud del carril guía medido es l - 2m, entonces la relación del error generado por los dos métodos de evaluación es:

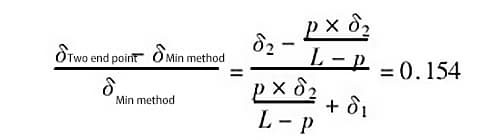
La relación del error generado por los dos métodos de evaluación es de 0,154, lo que significa que el error generado por el método de conexión de dos puntos es 15,4% mayor que el generado por el método de condición mínima.

En la ecuación anterior, cuando es decir, los puntos más alto y más bajo de la curva de error están infinitamente alejados, entoncesasí que tenemos:

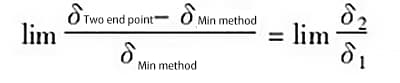
Por ejemplo, cuando δ1 = 1,0δ y δ2 = 0,25δ y la distancia entre los puntos más alto y más bajo de la curva de error es infinitamente distante (es decir, L=0,25), entonces la relación del error generado por los dos métodos de evaluación es lo que significa que el error generado por el método de conexión de dos puntos es 25% mayor que el generado por el método de condición mínima.

Cuando δ1 = δ2, es decir, la distancia entre los puntos más alto y más bajo de la curva de error es igual, como se muestra en la figura 6, los valores máximos de error generados por los dos métodos de evaluación son:

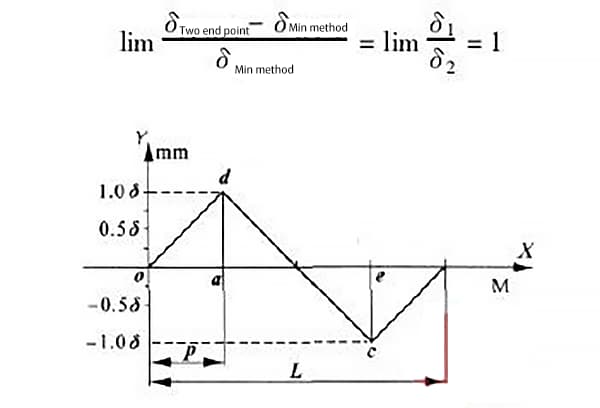
De ello se desprende que cuando los puntos más alto y más bajo del carril guía son iguales y están infinitamente alejados, el error máximo generado por los dos métodos de evaluación es el mayor y puede alcanzar 100%.

En el cuadro 1 figura la relación de los errores generados por los dos métodos de evaluación para diferentes longitudes del carril guía medido, cuando los puntos de la curva de error se distribuyen a ambos lados de la línea de conexión de dos puntos.

La distancia entre los puntos más alto y más bajo de la curva de error es igual cuando el paso de medición p = 0,5.

Cuadro 1 Coeficiente de error de dos métodos de evaluación

Ratio de error	Distancia L (M) entre los puntos más alto y más bajo del carril guía
1	10	15	20	25	30	40	∞
	33.30%	90%	93.30%	95%	96%	96.70%	97.50%

4. Conclusión

Si los puntos de la curva de error de rectitud están en el mismo lado de la línea de conexión de dos puntos, entonces los errores generados por los dos métodos de evaluación son cero, es decir, los resultados obtenidos con los dos métodos de evaluación son los mismos.

Si los puntos de la curva de error de rectitud están a ambos lados de la línea de conexión de dos puntos, y los puntos más alto y más bajo de la curva de error son iguales y están infinitamente alejados, entonces el error máximo generado por los dos métodos de evaluación es el mayor, y el error generado por el método de conexión de dos puntos puede ser 100% mayor que el generado por el método de condición mínima.

Por lo tanto, al evaluar el error de rectitud de los raíles guía de grandes máquinas herramienta en la producción práctica, es muy importante elegir el método de evaluación adecuado. Cuando los puntos de la curva de error se encuentran a ambos lados de la línea de conexión de dos puntos, el método de condición mínima se debe utilizar como la primera opción para la evaluación.