Imagínate que estás en un puente y ves pasar un camión pesado. ¿Te has preguntado alguna vez por qué el puente no se derrumba bajo su peso? Este artículo se sumerge en los conceptos de deformación y tensión, explicando cómo se deforman los materiales bajo una fuerza y cómo calculan los ingenieros estas deformaciones para garantizar la seguridad. Aprenderás las relaciones fundamentales entre estas fuerzas, cómo se miden y sus implicaciones prácticas en las estructuras cotidianas. Tanto si eres un ingeniero en ciernes como un simple curioso, esta guía arrojará luz sobre las fuerzas invisibles que mantienen intacto nuestro mundo.
En primer lugar, la mayor parte de la industria de control de seguridad consiste en medir la deformación de la estructura sometida a prueba. Una deformación excesiva puede provocar accidentes.
Por ejemplo, las grietas en las estructuras, el hundimiento y el desplazamiento entre la estructura y una referencia fija, son grandes deformaciones que pueden observarse a simple vista y que pueden medirse en milímetros utilizando medidores como los medidores de grietas, los niveles estáticos y los medidores de desplazamiento.
Pero, ¿cómo representar la pequeña deformación causada por la compresión en el interior de la estructura sometida a ensayo o la flexión en el exterior del objeto en forma de viga?
La respuesta es la tensión.
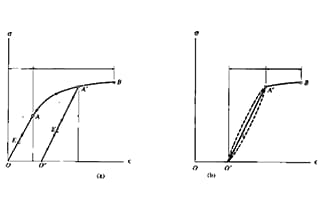
Supongamos que la longitud de una estructura con longitud L sufre una deformación bajo tensión y su longitud cambia a L', entonces su cambio de longitud ΔL = L' - L, y la deformación ε es la relación entre el cambio de longitud ΔL y la longitud original L, la fórmula es la siguiente:
Entonces, ¿cuál es la unidad de tensión?
Como se desprende de la fórmula, la deformación es una relación y es adimensional, es decir, no tiene unidad.
¿Qué es la microtensión?
Debido a que ΔL es muy pequeño, por lo general en el rango de micras, el valor calculado de la deformación es muy pequeño, con muchos decimales, lo que hace que sea inconveniente para mostrar y ver, por lo que se introduce la notación científica 10-6, llamada microstrain με, que se puede entender como la unidad de microstrain es 10-6, y nuestro rango de medición de la galga extensométrica es ±1500 microstrains, positivo indica estiramiento, y negativo indica compresión.
La deformación es una pequeña deformación en el interior de la estructura sometida a ensayo, ¿por qué se deforma? Porque está sometida a una fuerza externa.
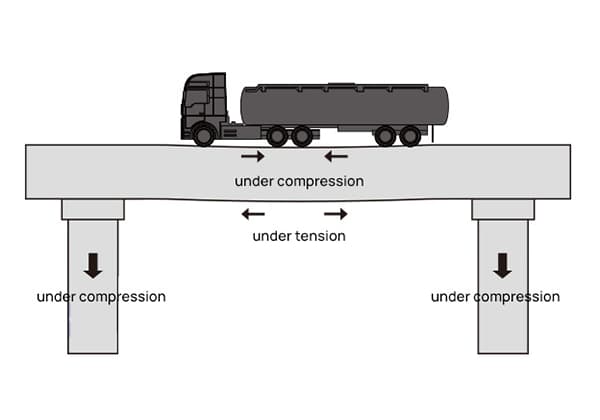
Tomando como ejemplo el muelle de un puente, si un camión a plena carga circula por el puente, el muelle soportará una presión adicional y producirá compresión y deformación por compresión, mientras que el muelle producirá una fuerza interna para contrarrestar la fuerza externa y superar la deformación.
Esta fuerza interna es la tensión. La tensión se define como la fuerza por unidad de superficie, que en realidad es presión, con unidades de MPa.
Entonces, ¿cuál es la relación entre la variable deformación y el cambio de tensión soportado? Consulte la fórmula de cálculo:
En la fórmula, σ representa la tensión, E es el módulo elástico del material ensayado, también conocido como módulo de Young, que es una magnitud física que describe la elasticidad del material.
Puede considerarse como la capacidad del material para resistir la deformación (rigidez) y, desde una perspectiva micro, es la fuerza de enlace entre átomos y moléculas.
Dos materiales con la misma deformación (el mismo valor de deformación), el material con una mayor resistencia a la deformación (un módulo elástico mayor) soportará una tensión mayor.
Por ejemplo, el tofu y el bloque de hierro del mismo tamaño, si su altura se comprime 1 mm, el primero sólo necesita ser presionado suavemente con la mano, mientras que el segundo debe ser ayudado por una herramienta.
El módulo elástico de los materiales de ingeniería comunes se puede encontrar en tablas, como el módulo elástico del hormigón C30 es 30000MPa (1N/mm2 = 1MPa), y el módulo elástico del acero al carbono es de 206GPa.
El módulo elástico Ec del hormigón a compresión y a tracción debe adoptarse de acuerdo con la tabla 4.1.5.
El módulo de deformación por cizallamiento Gc del hormigón puede adoptarse a 40% del valor del módulo elástico correspondiente.
La relación de Poisson Vc del hormigón puede adoptarse en 0,2.
Tabla4.15 Módulo elástico del hormigón (×104N/mm2).
| Grado de resistencia del hormigón | C15 | C20 | C25 | C30 | C35 | C40 | C45 | C50 | C55 | C60 | C65 | C70 | C75 | C80 |
| Ec | 2.20 | 2.55 | 2.80 | 3.00 | 3.15 | 3.25 | 3.35 | 3.45 | 3.55 | 3.60 | 3.65 | 3.70 | 3.75 | 3.80 |
Nota:
1. Cuando se dispone de datos de ensayo fiables, el módulo elástico puede determinarse a partir de los datos reales medidos;
2. Cuando se añade una gran cantidad de aditivos minerales al hormigón, el módulo elástico puede determinarse en función de los datos reales medidos según la edad especificada.
Tabla 1.1-13 Módulo elástico y coeficiente de Poisson de materiales de uso común
| Artículo | Módulo elástico E/GPa | Módulo de cizallamiento G/GPa | Relación de Poisson μ | Artículo | Módulo elástico E/GPa | Módulo de cizallamiento G/GPa | Teflón |
| Fundición gris | 118~126 | 44.3 | 0.3 | Zinc laminado | 82 | 31.4 | 0.27 |
| Fundición nodular | 173 | 0.3 | Plomo | 16 | 6.8 | 0.42 | |
| Acero al carbono, acero al cromo-níquel | 206 | 79.4 | 0.3 | Vidrio | 55 | 1.96 | 0.25 |
| Acero aleado | Vidrio orgánico | 2.35-29.42 | |||||
| Acero fundido | 202 | 0.3 | Goma | 0.0078 | 0.47 | ||
| Cobre puro laminado | 108 | 39.2 | 0.31-0.34 | Baquelita | 1.96-2.94 | 0.69-2.06 | 0.35-0.38 |
| Cobre puro estirado en frío | 127 | 48.0 | Plástico fenólico sándwich | 3.92-8.83 | |||
| Bronce al estaño fosforado laminado | 113 | 41.2 | 0.32-0.35 | Celuloide | 1.71-1.89 | 0.69-0.98 | 0.4 |
| Latón estirado en frío | 89-97 | 34.3-36.3 | 0.32-0.42 | Nylon 1010 | 1.07 | ||
| Bronce al manganeso laminado | 108 | 39.2 | 0.35 | Cloruro de polivinilo no plastificado | 3.14-3.92 | 0.35-0.38 | |
| Aluminio laminado | 68 | 25.5-26.5 | 0.32-0.36 | teflón | 1.14-1.42 | ||
| Alambre de aluminio trefilado | 69 | Polietileno de baja presión | 0.54-0.75 | ||||
| Aluminio fundido bronce | 103 | 41.1 | 0.3 | Polietileno de alta presión | 0.147-0.245 | ||
| Bronce al estaño fundido | 103 | 0.3 | hormigón | 13.73~39.2 | |||
| Aleación de duraluminio | 70 | 26.5 | 0.3 | 4.9-15.69 | 0.1-0.18 |
Al fin y al cabo, cuando las tensiones internas no pueden medirse directamente, la tensión puede calcularse midiendo la deformación y multiplicándola después por el módulo de ela del material.
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
AR 
DE 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO