Comprender la resistencia y la rigidez en Mecánica de Materiales

Prefacio

Para garantizar el rendimiento y la fiabilidad óptimos de un sistema o estructura mecánica, cada componente debe cumplir su función prevista con eficacia y eficiencia. El objetivo principal del diseño de seguridad de componentes de ingeniería es garantizar que todos los elementos posean la resistencia, rigidez y estabilidad adecuadas, asegurando así la integridad global y la longevidad del sistema.

La estabilidad es un concepto fundamental en ingeniería, que hace referencia a la capacidad de un componente para mantener o recuperar su estado de equilibrio original cuando se ve sometido a fuerzas externas. Este principio es crítico en diversos escenarios, como:

1. Deflexión lateral repentina de una columna esbelta sometida a compresión axial (pandeo de Euler).
2. Colapso de una columna de un edificio debido a un fallo de carga (inestabilidad estructural).
3. El pandeo de elementos de pared delgada sometidos a esfuerzos de compresión o cizalladura (pandeo local o global).

Estos ejemplos ilustran la importancia de la estabilidad para evitar fallos catastróficos y garantizar el funcionamiento seguro de sistemas y estructuras mecánicas.

En este debate, me centraré en dilucidar mi comprensión global de dos principios de ingeniería igualmente cruciales: la rigidez y la resistencia. Estos conceptos, junto con la estabilidad, forman la tríada de consideraciones fundamentales en el diseño de la seguridad de los componentes, y cada uno de ellos desempeña un papel vital en la determinación del rendimiento general, la durabilidad y la seguridad de los sistemas de ingeniería.

Fuerza

¿Qué es la fuerza?

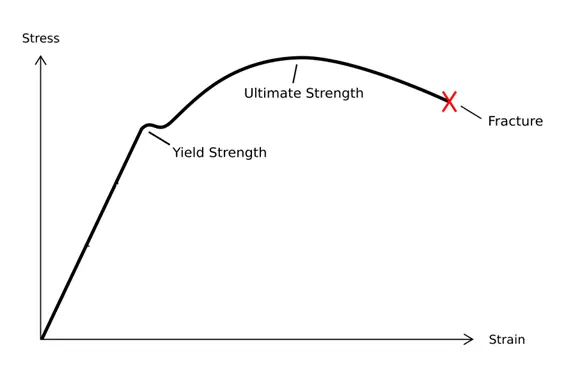
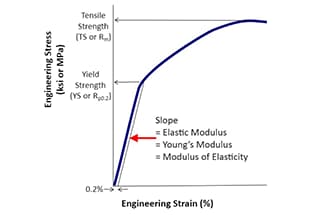
Definición: La resistencia es la capacidad de los materiales, componentes o estructuras para soportar cargas o fuerzas aplicadas sin fallar, sufrir deformaciones excesivas o daños. Es una propiedad fundamental en la ciencia y la ingeniería de materiales que determina la capacidad de un material para resistir esfuerzos mecánicos.

La fuerza abarca varios aspectos, entre ellos:

1. Resistencia a la tracción: Es la tensión máxima que puede soportar un material sometido a fuerzas de estiramiento antes de fallar.
2. Resistencia a la compresión: Es la tensión máxima que puede soportar un material sometido a fuerzas de compresión antes de fallar.
3. Límite elástico: Tensión a la que un material comienza a deformarse plásticamente.
4. Resistencia al cizallamiento: Capacidad de resistir fuerzas que provocan el deslizamiento interno de un material a lo largo de un plano paralelo a la dirección de la fuerza.

Por ejemplo, en la fabricación de metales, comprender la resistencia de los materiales es crucial para diseñar componentes que puedan soportar cargas operativas. Una viga de acero de un edificio debe tener la resistencia suficiente para soportar el peso de la estructura y cargas adicionales sin doblarse ni romperse.

En la resistencia influyen varios factores, entre ellos:

• Composición del material y microestructura
• Tratamiento térmico y métodos de transformación
• Condiciones ambientales (temperatura, corrosión)
• Ritmo y duración de la carga

La unidad de medida de la resistencia suele expresarse en megapascales (MPa) o libras por pulgada cuadrada (psi) en unidades imperiales. Por ejemplo, el acero dulce tiene una resistencia a la tracción de aproximadamente 400-550 MPa, mientras que los aceros aleados de alta resistencia pueden superar los 1000 MPa.

En fabricación e ingeniería, los cálculos y ensayos de resistencia son esenciales para:

• Selección de materiales adecuados para aplicaciones específicas
• Diseño de componentes con un rendimiento y unos factores de seguridad óptimos
• Predicción de la vida útil y los modos de fallo de los productos
• Garantizar el cumplimiento de las normas y reglamentos del sector

A menudo se emplean técnicas avanzadas como el análisis de elementos finitos (FEA) y los ensayos destructivos para evaluar y validar la resistencia de materiales y componentes en aplicaciones complejas de ingeniería.

Tipos de fallo en función de la resistencia

Fractura frágil: Modo de fallo repentino y catastrófico caracterizado por una rápida propagación de la grieta con una deformación plástica mínima. Este tipo de fallo se produce sin previo aviso y suele dar lugar a una superficie de fractura limpia y plana.

Por ejemplo:

1. Fractura abrupta de una probeta de fundición a lo largo de su sección transversal durante un ensayo de tracción uniaxial, que presenta un aspecto cristalino en la superficie de fractura.
2. Fallo repentino de una muestra de hierro fundido con sección transversal circular a lo largo de un plano oblicuo durante un ensayo de torsión, demostrando un patrón de fractura helicoidal.

Rendimiento del plástico: Modo de fallo en el que el material experimenta una deformación plástica significativa, lo que provoca un cambio de forma permanente y la pérdida de la integridad estructural. Este tipo de fallo suele ser más gradual y observable que la fractura frágil.

Por ejemplo:

1. Durante el ensayo de tracción, una probeta de acero con bajo contenido en carbono presenta un cuello y un alargamiento considerables antes del fallo final, con una superficie de fractura en forma de cono y copa característica.
2. En torsión, una muestra de acero bajo en carbono experimenta una deformación angular y un alabeo significativos antes de fallar, a menudo acompañados de distorsiones visibles de la superficie.

Es importante tener en cuenta que el modo de fallo de un material depende de varios factores, como las propiedades del material, las condiciones de carga, la temperatura y los factores ambientales. Algunos materiales pueden mostrar una transición de comportamiento dúctil a frágil en determinadas condiciones, como bajas temperaturas o altas velocidades de deformación.

Teoría de la fuerza

1. Teoría de la tensión máxima de tracción:

Cuando la tensión máxima de tracción σ1 en un punto del elemento alcanza la tensión última σb en condiciones de tensión unidireccional, el material sufrirá una fractura frágil. Así pues, los criterios para el fallo por rotura frágil de componentes con puntos críticos en condiciones de tensión complejas son: σ1 = σb.

En consecuencia, las condiciones de resistencia establecidas por el primer teoría de la fuerza son: σ1 ≤ σb.

2. Teoría de la deformación máxima por tracción:

Cuando la tensión máxima de tracción ε1 alcanza el valor límite εu en condiciones de tensión unidireccional, el material fallará debido a la fractura frágil. Esto puede expresarse como ε1 = εu.

A partir de la Ley de Hooke generalizada, podemos calcular ε1 como: ε1 = [σ1 - u(σ2 + σ3)] / E, por lo que σ1 - u(σ2 + σ3) = σb.

Las condiciones de resistencia establecidas por la segunda teoría de la resistencia son: σ1 - u(σ2 + σ3) ≤ σb.

3. Teoría del esfuerzo cortante máximo:

Cuando el esfuerzo cortante máximo τMax alcanza el esfuerzo cortante último τ0 bajo condiciones de esfuerzo unidireccional, el material fallará debido a la fluencia. Esto puede expresarse como τMax = τ0.

La fórmula del esfuerzo cortante en una sección inclinada durante la tracción axial es τ0 = σs/2 (siendo σs el esfuerzo normal en la sección transversal). La fórmula para τMax es (σ1 - σ3)/2. Por lo tanto, la condición de daño puede reescribirse como σ1 - σ3 = σs.

La condición de resistencia establecida por la tercera teoría de la resistencia es: σ1 - σ3 ≤ σs.

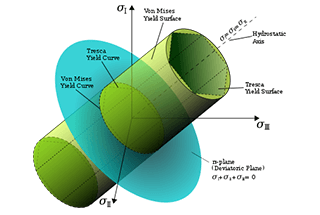
4. Teoría de la energía específica del cambio de forma:

Cuando la relación de cambio de forma en un punto del elemento alcanza el valor límite en condiciones de tensión unidireccional, el material fallará debido a la fluencia.

La condición de resistencia establecida por la cuarta teoría de la resistencia es:

√(σ1^2 + σ2^2 + σ3^2 - σ1σ2 - σ2σ3 - σ3σ1) < σs.

2. Rigidez

Qué es la rigidez

Definición: La rigidez se refiere a la capacidad de un material, componente o estructura para resistir la deformación elástica o el desplazamiento cuando se somete a una fuerza externa. Cuantifica el grado en que un sistema puede mantener su forma y dimensiones dentro de los límites permitidos bajo las cargas aplicadas.

La rigidez es un parámetro fundamental en ingeniería que caracteriza la relación entre fuerza y deformación en un material o estructura. Se define como la relación entre la fuerza aplicada y el desplazamiento resultante, indicando la cantidad de fuerza necesaria para producir una unidad de deformación. En términos matemáticos, la rigidez (k) se expresa como:

k = F / δ

Dónde:

• F = fuerza aplicada
• δ = desplazamiento resultante

La unidad de rigidez suele ser la fuerza por unidad de longitud, como N/m (newtons por metro) en el sistema SI o lbf/in (libras-fuerza por pulgada) en el sistema imperial.

En términos prácticos, la rigidez puede conceptualizarse utilizando la analogía de un muelle. La constante del muelle, que representa la rigidez de un muelle, se define como la relación entre la fuerza de tracción o compresión aplicada y la elongación o compresión resultante. Esta relación se describe mediante la Ley de Hooke para sistemas elásticos lineales.

Comprender y controlar la rigidez es crucial en diversas aplicaciones de ingeniería, entre ellas:

1. Diseño estructural: Garantizar que los edificios y puentes puedan soportar cargas sin deformaciones excesivas.
2. Componentes mecánicos: Diseño de piezas que mantienen la precisión bajo cargas de funcionamiento
3. Control de vibraciones: Gestión de la respuesta dinámica de los sistemas a las cargas cíclicas
4. Selección de materiales: Elección de materiales adecuados para aplicaciones específicas en función de sus propiedades de rigidez.

Los ingenieros deben equilibrar los requisitos de rigidez con otras consideraciones de diseño como la resistencia, el peso, el coste y la fabricabilidad para crear soluciones óptimas para aplicaciones específicas.

Tipo de rigidez:

Cuando la carga aplicada es constante, se denomina rigidez estática.

Cuando la carga se alterna, se denomina rigidez dinámica.

La rigidez estática engloba la rigidez estructural y la rigidez de contacto.

La rigidez estructural se refiere a la rigidez del propio elemento e incluye la rigidez a la flexión y la rigidez a la torsión.

1. Rigidez a la flexión: calculada según la fórmula siguiente:

K=P/δ

Dónde

• P - carga estática (n);
• δ-- Deformación elástica en la dirección de la carga（ μm)。

2. La rigidez a la torsión se calcula según la fórmula siguiente:

K_m=ML/θ

Donde M - par aplicado (n - m);

L - distancia desde la posición de acción del par hasta el extremo fijo (m);

θ-- Ángulo de torsión (°)

3. Relación entre resistencia y rigidez

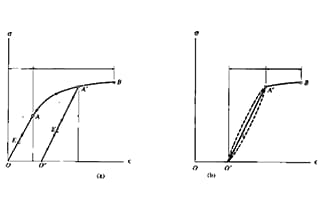
De la explicación anterior de la resistencia y la rigidez se desprende que la resistencia se centra en el fallo bajo una fuerza externa y se clasifica en límite elástico plástico y fallo por fractura frágil, que está relacionado con la curva tensión-deformación durante el ensayo de tracción. En cambio, la rigidez se refiere a la relación entre la deformación y la fuerza.

Como se muestra en la fig.

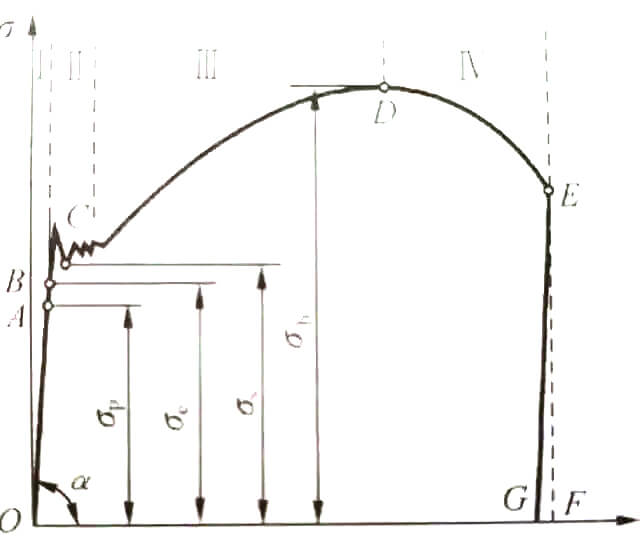
La curva de la figura puede dividirse en cuatro etapas:

1. Etapa de deformación elástica;

2. Fase de rendimiento;

3. Etapa de refuerzo;

4. Etapa de necking local.

La rigidez se define como la resistencia a la deformación elástica, que se produce en la fase inicial, y se rige por la ley de Hooke en condiciones elásticas.

Cálculo de la rigidez a la flexión y la rigidez a la torsión bajo cargas estáticas es similar a la ley de Hooke, lo que sugiere que la rigidez sólo se mide durante la fase de deformación elástica.

En la etapa siguiente, cuando se produce la deformación plástica durante el ensayo de tracción, la deformación residual no desaparece. En la curva tensión-deformación, aunque la tensión permanece casi invariable, la deformación aumenta considerablemente. En este punto, la tensión alcanza el límite elástico y el material entra en la fase de límite elástico plástico. A medida que la tensión sigue aumentando, la deformación también aumenta hasta alcanzar el límite de resistencia.

Por lo tanto, la medición de la resistencia se produce después de que el material sufra una deformación elástica y antes de que alcance el límite de resistencia.

Envuélvalo

En conclusión, tanto la rigidez como la resistencia se evalúan durante la fase de fallo de las piezas, midiéndose la rigidez por la tensión y la resistencia por la deformación.

En cuanto a su orden en el proceso de deformación, la rigidez se produce en la fase anterior, mientras que la resistencia se produce en la fase posterior.

Por lo tanto, al evaluar las condiciones de fallo de las piezas, siempre que se cumplan los requisitos de rigidez, la pieza debería poder soportar una tensión suficiente durante la fase de deformación elástica, que a su vez debería cumplir los requisitos de resistencia.

Esta relación se refleja en diversos diseños, como el eje de los equipos mecánicos. Normalmente, el tamaño del eje se determina en función de las condiciones de resistencia y, a continuación, se verifica su rigidez en función de las condiciones de rigidez.

Por lo tanto, los requisitos de rigidez de los ejes de maquinaria de precisión son muy elevados, y el diseño del tamaño de su sección transversal suele estar controlado por las condiciones de rigidez.