¿Alguna vez se ha preguntado cómo calcular con precisión el peso de una malla metálica? En esta entrada del blog, exploraremos varios métodos y factores a tener en cuenta a la hora de determinar el peso de una malla metálica. Nuestro experto residente en ingeniería mecánica le guiará a través del proceso, proporcionándole ideas y ejemplos prácticos. Al final de este artículo, sabrá cómo calcular el peso de una malla metálica en función de sus necesidades específicas.
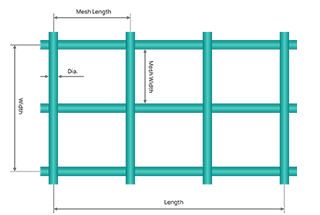
El cálculo del peso de las mallas metálicas es crucial en diversas aplicaciones, desde la construcción hasta la fabricación industrial. Saber calcular con precisión el peso de una malla metálica garantiza que los proyectos se lleven a cabo de forma eficaz, segura y ajustada al presupuesto. El peso de la malla metálica puede verse influido por varios factores, como el tipo de material, el diámetro del alambre, el número de mallas y las dimensiones totales.

Diámetro del alambre: El grosor del alambre utilizado en la malla es un factor primordial. Se mide en milímetros (mm) o pulgadas. Los alambres más gruesos producirán una malla más pesada. Por ejemplo, un alambre de 2 mm de diámetro producirá una malla más pesada que un alambre de 1 mm de diámetro, suponiendo que todos los demás factores sean constantes. Esto se debe a que el volumen del alambre aumenta con el cuadrado del diámetro, lo que repercute significativamente en el peso.
Número de malla: Se refiere al número de aberturas por pulgada lineal de la malla. Un mayor número de mallas significa más alambres y, en consecuencia, más peso por unidad de superficie. Por ejemplo, una malla con 10 aberturas por pulgada (malla 10) será más ligera que una malla con 20 aberturas por pulgada (malla 20) si el diámetro del alambre sigue siendo el mismo. Esto se debe a la mayor densidad de alambres en el número de mallas más alto.
Apertura de malla: El tamaño de las aberturas entre los alambres, medido de centro a centro para la malla y de dentro a dentro para las aberturas, también afecta al peso. Las aberturas más pequeñas dan como resultado una malla más densa y pesada. Por ejemplo, una malla con una abertura de 1 mm será más pesada que una con una abertura de 5 mm, suponiendo que el diámetro de los alambres y el número de mallas sean los mismos.
Tipo de material: Los distintos materiales tienen densidades diferentes, lo que afecta directamente al peso. Los materiales más comunes son el acero inoxidable, el acero dulce, el aluminio, el latón y el cobre. Por ejemplo, el acero inoxidable tiene una densidad aproximada de 7,93 g/cm³, mientras que el aluminio tiene una densidad de unos 2,70 g/cm³. Esto significa que, para un mismo volumen, el acero inoxidable será mucho más pesado que el aluminio.
Dimensiones: La anchura y la longitud del rollo o panel de malla metálica también influyen en el peso total. Normalmente se miden en metros o pies. Por ejemplo, un panel de malla metálica de 10 metros por 1 metro pesará más que un panel de 5 metros por 1 metro si todos los demás factores son idénticos.
Introduzca la anchura, la longitud, la anchura de malla, la longitud de malla y el diámetro de la malla metálica en la calculadora que aparece a continuación y obtendrá el resultado del peso de la malla metálica en kg y lbs.
Calcular el peso de una malla metálica es esencial. Garantiza una planificación precisa en diversos proyectos industriales y de construcción. El cálculo del peso depende del diámetro del alambre, el número de mallas, la densidad del material y las dimensiones.
El método de cálculo del peso de las mallas metálicas puede determinarse de varias maneras, en función del material, la estructura de la malla y los parámetros específicos necesarios para el cálculo. Podemos resumir varios métodos de cálculo y factores a tener en cuenta.
En primer lugar, un método básico de cálculo del peso consiste en estimar dividiendo por 2 el producto del diámetro del alambre, el número de mallas, la longitud de la malla y la anchura de la malla. Este método es aplicable a los cálculos generales del peso de las mallas metálicas, en los que la unidad del diámetro del alambre es el milímetro (mm) y las unidades de la longitud y la anchura de la malla son el metro (m).
Además, para determinados tipos de malla metálica, como la galvanizada, pueden emplearse métodos de cálculo más detallados. Por ejemplo, el peso de la malla de alambre galvanizado puede calcularse midiendo la longitud del alambre por metro cuadrado (en metros) y el peso del alambre por metro (en kilogramos). Este método proporciona una forma sencilla de estimar el peso de la malla metálica.
Otro método consiste en calcular el peso mediante el área de la sección transversal y la longitud del alambre, así como la densidad del material. Esto se puede conseguir mediante la fórmula "Peso(kg) = Área de la sección transversal(mm2) × Longitud(m) × Densidad(g/cm3) × 1/1000″. Este método es adecuado para situaciones en las que se requiere un cálculo preciso del peso de la malla metálica, especialmente cuando se considera la densidad de diferentes materiales.
La siguiente fórmula simplificada puede utilizarse para calcular el peso de la malla de alambre de acero.
Peso (kg) = longitud total de las materias primas * diámetro del hilo² * coeficiente (0,00617)
Malla metálica de acero inoxidable
El acero inoxidable se utiliza habitualmente por su resistencia a la corrosión y su solidez. Para malla de alambre de acero inoxidable:
Malla metálica de acero dulce
El acero dulce es conocido por su durabilidad y asequibilidad. El cálculo de las mallas de acero dulce es similar al del acero inoxidable, pero utiliza un factor de densidad diferente:
Malla metálica de aluminio
El aluminio es apreciado por su ligereza y su resistencia a la corrosión. Para malla de alambre de aluminio:
Malla metálica de latón y cobre
El latón y el cobre se utilizan por su excelente conductividad eléctrica y su atractivo estético. Para estos materiales:
Para el latón:
Para el cobre:
Para ilustrarlo, calculemos el peso de una malla metálica de acero inoxidable con las siguientes especificaciones:
Utilizando la fórmula general:
Para acero inoxidable:
Para el peso total:
Comprendiendo estos factores y aplicando las fórmulas adecuadas, es posible calcular con precisión el peso de las mallas metálicas, lo que garantiza una planificación y ejecución precisas en diversos proyectos.
En la tabla siguiente se indica el peso teórico de las mallas de acero en kg/m². Si su tamaño de acero no figura en la tabla siguiente, puede utilizar nuestro calculadora del peso del acero calcular en línea.
(1) Refuerzo longitudinal peso de la barra gráfico
| Grado | Barra de refuerzo longitudinal | Peso teórico | ||
| Dia. | Distancia | Superficie por metro lineal | ||
| (mm) | (mm) | (mm²/m) | (kg/m²) | |
| A18 | 18 | 200 | 1273 | 14.43 |
| A16 | 16 | 200 | 1006 | 12.34 |
| A14 | 14 | 200 | 770 | 10.49 |
| A12 | 12 | 200 | 566 | 8.88 |
| A11 | 11 | 200 | 475 | 7.46 |
| A10 | 10 | 200 | 393 | 6.16 |
| A9 | 9 | 200 | 318 | 4.99 |
| A8 | 8 | 200 | 252 | 3.95 |
| A7 | 7 | 200 | 193 | 3.02 |
| A6 | 6 | 200 | 142 | 2.22 |
| A5 | 5 | 200 | 98 | 1.54 |
| B18 | 18 | 100 | 2545 | 24.42 |
| B16 | 16 | 100 | 2011 | 18.89 |
| B14 | 14 | 100 | 1539 | 15.19 |
| B12 | 12 | 100 | 1131 | 10.9 |
| B11 | 11 | 100 | 950 | 9.43 |
| B10 | 10 | 100 | 785 | 8.14 |
| B9 | 9 | 100 | 635 | 6.97 |
| B8 | 8 | 100 | 503 | 5.93 |
| B7 | 7 | 100 | 385 | 4.53 |
| B6 | 6 | 100 | 283 | 3.73 |
| B5 | 5 | 100 | 196 | 3.05 |
| C18 | 18 | 150 | 1697 | 17.77 |
| C16 | 16 | 150 | 1341 | 14.98 |
| C14 | 14 | 150 | 1027 | 12.51 |
| C12 | 12 | 150 | 754 | 10.36 |
| C11 | 11 | 150 | 634 | 8.7 |
| C10 | 10 | 150 | 523 | 7.19 |
| C9 | 9 | 150 | 423 | 5.82 |
| C8 | 8 | 150 | 335 | 4.61 |
| C7 | 7 | 150 | 257 | 3.53 |
| C6 | 6 | 150 | 189 | 2.6 |
| C5 | 5 | 150 | 131 | 1.8 |
| D18 | 18 | 100 | 1545 | 28.86 |
| D16 | 16 | 100 | 2011 | 24.68 |
| D14 | 14 | 100 | 1539 | 20.98 |
| D12 | 12 | 100 | 1131 | 17.75 |
| D11 | 11 | 100 | 950 | 14.92 |
| D10 | 10 | 100 | 785 | 12.33 |
| D9 | 9 | 100 | 635 | 9.98 |
| D8 | 8 | 100 | 503 | 7.9 |
| D7 | 7 | 100 | 385 | 6.04 |
| D6 | 6 | 100 | 283 | 4.44 |
| D5 | 5 | 100 | 196 | 3.08 |
| E18 | 18 | 150 | 1697 | 19.25 |
| E16 | 16 | 150 | 1341 | 16.46 |
| E14 | 14 | 150 | 1027 | 13.99 |
| E12 | 12 | 150 | 754 | 11.84 |
| E11 | 11 | 150 | 634 | 9.95 |
| E10 | 10 | 150 | 523 | 8.22 |
| E9 | 9 | 150 | 423 | 6.66 |
| E8 | 8 | 150 | 335 | 5.26 |
| E7 | 7 | 150 | 257 | 4.03 |
| E6 | 6 | 150 | 189 | 2.96 |
| E5 | 5 | 150 | 131 | 2.05 |
| F18 | 18 | 100 | 2545 | 25.9 |
| F16 | 16 | 100 | 2011 | 21.7 |
| F14 | 14 | 100 | 1539 | 18 |
| F12 | 12 | 100 | 1131 | 14.8 |
| F11 | 11 | 100 | 950 | 12.43 |
| F10 | 10 | 100 | 785 | 10.28 |
| F9 | 9 | 100 | 635 | 8.32 |
| F8 | 8 | 100 | 503 | 6.58 |
| F7 | 7 | 100 | 385 | 5.03 |
| F6 | 6 | 100 | 283 | 3.7 |
| F5 | 5 | 100 | 196 | 2.57 |
(2) Tabla de pesos de la armadura transversal
| Grado | Barra de refuerzo transversal | Peso teórico | ||
| Dia. | Distancia | Superficie por metro lineal | ||
| (mm) | (mm) | (mm²/m) | (kg/m²) | |
| A18 | 12 | 200 | 566 | 14.43 |
| A16 | 12 | 200 | 566 | 12.34 |
| A14 | 12 | 200 | 566 | 10.49 |
| A12 | 12 | 200 | 566 | 8.88 |
| A11 | 11 | 200 | 475 | 7.46 |
| A10 | 10 | 200 | 393 | 6.16 |
| A9 | 9 | 200 | 318 | 4.99 |
| A8 | 8 | 200 | 252 | 3.95 |
| A7 | 7 | 200 | 193 | 3.02 |
| A6 | 6 | 200 | 142 | 2.22 |
| A5 | 5 | 200 | 98 | 1.54 |
| B18 | 12 | 200 | 566 | 24.42 |
| B16 | 10 | 200 | 393 | 18.89 |
| B14 | 10 | 200 | 393 | 15.19 |
| B12 | 8 | 200 | 252 | 10.9 |
| B11 | 8 | 200 | 252 | 9.43 |
| B10 | 8 | 200 | 252 | 8.14 |
| B9 | 8 | 200 | 252 | 6.97 |
| B8 | 8 | 200 | 252 | 5.93 |
| B7 | 7 | 200 | 193 | 4.53 |
| B6 | 7 | 200 | 193 | 3.73 |
| B5 | 7 | 200 | 193 | 3.05 |
| C18 | 12 | 200 | 566 | 17.77 |
| C16 | 12 | 200 | 566 | 14.98 |
| C14 | 12 | 200 | 566 | 12.51 |
| C12 | 12 | 200 | 566 | 10.36 |
| C11 | 11 | 200 | 475 | 8.7 |
| C10 | 10 | 200 | 393 | 7.19 |
| C9 | 9 | 200 | 318 | 5.82 |
| C8 | 8 | 200 | 252 | 4.61 |
| C7 | 7 | 200 | 193 | 3.53 |
| C6 | 6 | 200 | 142 | 2.6 |
| C5 | 5 | 200 | 98 | 1.8 |
| D18 | 12 | 100 | 1131 | 28.86 |
| D16 | 12 | 100 | 1131 | 24.68 |
| D14 | 12 | 100 | 1131 | 20.98 |
| D12 | 12 | 100 | 1131 | 17.75 |
| D11 | 11 | 100 | 950 | 14.92 |
| D10 | 10 | 100 | 785 | 12.33 |
| D9 | 9 | 100 | 635 | 9.98 |
| D8 | 8 | 100 | 503 | 7.9 |
| D7 | 7 | 100 | 385 | 6.04 |
| D6 | 6 | 100 | 283 | 4.44 |
| D5 | 5 | 100 | 196 | 3.08 |
| E18 | 12 | 150 | 754 | 19.25 |
| E16 | 12 | 150 | 754 | 16.46 |
| E14 | 12 | 150 | 754 | 13.99 |
| E12 | 12 | 150 | 754 | 11.84 |
| E11 | 11 | 150 | 634 | 9.95 |
| E10 | 10 | 150 | 523 | 8.22 |
| E9 | 9 | 150 | 423 | 6.66 |
| E8 | 8 | 150 | 335 | 5.26 |
| E7 | 7 | 150 | 257 | 4.03 |
| E6 | 6 | 150 | 189 | 2.96 |
| E5 | 5 | 150 | 131 | 2.05 |
| F18 | 12 | 150 | 754 | 25.9 |
| F16 | 12 | 150 | 754 | 21.7 |
| F14 | 12 | 150 | 754 | 18 |
| F12 | 12 | 150 | 754 | 14.8 |
| F11 | 11 | 150 | 634 | 12.43 |
| F10 | 10 | 150 | 523 | 10.28 |
| F9 | 9 | 150 | 423 | 8.32 |
| F8 | 8 | 150 | 335 | 6.58 |
| F7 | 7 | 150 | 257 | 5.03 |
| F6 | 6 | 150 | 189 | 3.7 |
| F5 | 5 | 150 | 131 | 2.57 |
El cálculo preciso del peso de las mallas metálicas es esencial para diversas aplicaciones, desde la construcción hasta la fabricación. Comprender los factores que influyen en estos cálculos garantiza la precisión y la fiabilidad, cruciales para una planificación y una estimación de costes eficaces.
El diámetro del alambre, medido en milímetros (mm), influye significativamente en el peso de la malla metálica. El peso aumenta con el cuadrado del diámetro del alambre. Por ejemplo, si un alambre de 2 mm de diámetro pesa 1 kg por metro, un alambre de 4 mm de diámetro pesará 4 kg por metro, suponiendo que los demás factores permanezcan constantes. Esta relación exponencial subraya la importancia de medir con precisión el diámetro del alambre.
El número de mallas se refiere al número de aberturas por pulgada en la malla metálica. Un mayor número de mallas significa más alambres en un área determinada, lo que aumenta el peso total. Por ejemplo, una malla de 20 alambres (20 aberturas por pulgada) pesará más que una malla de 10 alambres (10 aberturas por pulgada) con el mismo diámetro de alambre. El número de mallas influye directamente en la densidad y el peso de la malla.
Las dimensiones del rollo de malla metálica, incluidas la longitud y la anchura, influyen significativamente en el peso total. Estas dimensiones suelen medirse en metros o pies. Por ejemplo, un rollo de malla metálica de 10 metros de longitud y 1 metro de anchura pesará más que un rollo de 5 metros por 1 metro, suponiendo que el diámetro del alambre y el número de mallas sean los mismos. Medir con precisión las dimensiones del rollo es esencial para calcular el peso total.
Las tolerancias de fabricación pueden introducir variaciones en el diámetro del alambre, el número de mallas y las dimensiones de los rollos. Estas variaciones pueden afectar a los cálculos de peso, dando lugar a discrepancias entre los pesos calculados y los reales. Tenga en cuenta las posibles variaciones y tolerancias de fabricación para garantizar la precisión.
Los distintos materiales tienen densidades diferentes, lo que afecta directamente al peso de la malla metálica. Los materiales más comunes son el acero inoxidable, el acero dulce, el aluminio, el latón y el cobre, cada uno con su densidad específica. Por ejemplo, el acero inoxidable tiene una densidad aproximada de 7,93 g/cm³, mientras que el aluminio tiene una densidad de unos 2,70 g/cm³. Ajuste la fórmula del peso general para incorporar la densidad específica del material y realizar cálculos precisos.
Las mallas metálicas pueden recubrirse con materiales como cinc (galvanizado), PVC u otros revestimientos protectores para aumentar su durabilidad y resistencia a la corrosión. Estos revestimientos aumentan el peso total de la malla metálica. Por ejemplo, la malla galvanizada pesará más que la no recubierta debido a la capa adicional de zinc. Tenga en cuenta el peso de los revestimientos al realizar los cálculos.
Los tratamientos térmicos, como el recocido o el endurecimiento, pueden alterar las propiedades físicas de la malla metálica, lo que puede afectar a su peso. Aunque el impacto en el peso puede ser mínimo, sigue siendo importante tener en cuenta cualquier cambio en las propiedades del material derivado de los tratamientos térmicos.
Las variaciones de temperatura pueden provocar la dilatación o contracción térmica de la malla metálica, afectando a sus dimensiones y peso. Por ejemplo, las temperaturas elevadas pueden provocar la dilatación de la malla metálica, lo que conlleva un ligero aumento del peso por unidad de superficie. Tenga en cuenta las condiciones de temperatura de funcionamiento al calcular el peso para aplicaciones específicas.
La humedad puede afectar al peso de determinados materiales de malla metálica, en particular los propensos a la corrosión o la oxidación. Por ejemplo, las mallas metálicas de acero dulce sin recubrimiento pueden absorber la humedad del ambiente, aumentando su peso con el tiempo. Tener en cuenta la humedad ambiental es crucial para las aplicaciones en las que la malla metálica está expuesta a distintos niveles de humedad.
Comprender y tener en cuenta estos factores garantiza un cálculo preciso del peso de la malla metálica, lo que contribuye a una planificación precisa, una estimación de costes y una ejecución eficaz del proyecto.
A continuación encontrará respuestas a algunas preguntas frecuentes:
Para calcular el peso de una malla de acero inoxidable, hay que tener en cuenta el diámetro del alambre, el número de mallas (número de mallas por pulgada) y las dimensiones del panel de malla. A continuación se indican los pasos y fórmulas para los distintos tipos de malla:
Para la malla soldada de acero inoxidable de agujero cuadrado, la fórmula es:
Como alternativa, puede utilizar:
Por ejemplo, si tiene una malla de acero inoxidable con un diámetro de alambre de 0,12 mm, un número de mallas de 80 por pulgada y unas dimensiones de 1 metro por 30 metros:
Para la malla soldada de acero inoxidable con orificio rectangular, la fórmula es:
Una fórmula general aplicable a cualquier forma es:
Por ejemplo, para una malla soldada galvanizada con un diámetro de alambre de 0,9 mm, un tamaño de malla de 1/2 pulgada x 1/2 pulgada y unas dimensiones de 3 pies por 100 pies:
Puntos clave que hay que recordar:
Utilizando estas fórmulas y asegurándose de que todas las medidas están en las unidades correctas, puede calcular con precisión el peso de la malla de acero inoxidable para sus requisitos específicos.
La precisión de los cálculos del peso de las mallas metálicas depende de varios factores clave. En primer lugar, el diámetro del alambre es crucial, ya que cualquier imprecisión en su medición puede afectar significativamente al peso total. Es esencial medirlo con precisión utilizando herramientas como un calibre o un micrómetro. En segundo lugar, el número de mallas, que indica el número de agujeros por pulgada, y el tamaño de la abertura, o el espacio entre los alambres, son parámetros críticos. Estos factores determinan la densidad y el área abierta de la malla, lo que afecta a su peso. Es necesario medir con precisión estos parámetros para realizar cálculos exactos.
Además, la longitud y la anchura de la malla deben medirse con precisión, ya que influyen directamente en el cálculo del peso. La densidad del material también desempeña un papel importante; los distintos materiales, como el acero inoxidable o el cobre, tienen densidades diferentes que deben tenerse en cuenta en el cálculo. Utilizar la fórmula correcta para calcular el peso es vital, ya que se requieren fórmulas diferentes para las mallas metálicas de tejido liso o de sarga y las mallas metálicas de tejido holandés.
La precisión en la medición de todos los parámetros -diámetro del alambre, número de mallas, longitud y anchura- es crucial para evitar errores que puedan dar lugar a imprecisiones. Por último, los factores ambientales y de manipulación, como la deformación o los daños debidos a un almacenamiento o una manipulación inadecuados, pueden afectar indirectamente al cálculo del peso al alterar las dimensiones de la malla. Teniendo en cuenta estos factores y utilizando medidas exactas y fórmulas adecuadas, el peso de la malla metálica puede calcularse con gran precisión.
El diámetro del alambre influye significativamente en el peso de la malla metálica a través de varios factores clave. En primer lugar, el peso de la malla metálica es directamente proporcional al cuadrado del diámetro del alambre. Esto significa que a medida que aumenta el diámetro del alambre, el peso de la malla aumenta exponencialmente. La relación puede representarse mediante la fórmula Peso = (diámetro del alambre)² x malla x longitud x anchura. Esta fórmula pone de manifiesto que el peso es una función del diámetro del alambre al cuadrado, lo que indica un aumento sustancial del peso incluso con pequeños aumentos del diámetro.
Un diámetro de alambre más grueso da como resultado una malla más resistente y duradera, pero también reduce el tamaño de las aberturas entre los alambres. Este mayor volumen de material contribuye a un mayor peso total. La medición precisa del diámetro del alambre, normalmente con un micrómetro o un calibre, es crucial, ya que afecta directamente al cálculo del peso.
El tamaño de la apertura, que es la distancia entre dos alambres adyacentes, se determina restando el diámetro del alambre del paso (la distancia entre los centros de dos alambres adyacentes). Aunque el tamaño de la apertura en sí no calcula el peso, está influido por el diámetro del alambre, que a su vez afecta al peso.
En la práctica, los alambres más gruesos requieren más material, lo que se traduce en un aumento del peso total de la malla. Esto es especialmente importante en aplicaciones en las que el peso es un factor crítico, como las industrias aeroespacial o de la construcción. Además, las tolerancias estándar de los diámetros de los alambres pueden provocar variaciones en el peso final de la malla. Por ejemplo, los márgenes de tolerancia específicos para las mallas de acero inoxidable pueden afectar al peso final.
En conclusión, el diámetro del alambre es un parámetro crucial que influye directamente en el peso de la malla metálica. A medida que aumenta el diámetro del alambre, también aumenta el peso de la malla debido al mayor volumen de material utilizado, lo que aumenta la resistencia y durabilidad de la malla.
Sí, se puede calcular el peso de la malla metálica para distintos materiales utilizando una fórmula general, pero hay que hacer ajustes específicos para cada material para garantizar la precisión. La fórmula general para calcular el peso de las mallas metálicas suele incluir parámetros como el diámetro del alambre, el número de mallas (número de mallas por pulgada), la anchura y la longitud de la malla.
La fórmula básica es:
Esta fórmula suele aplicarse a materiales como el acero inoxidable, el hierro y el acero. Sin embargo, para otros metales como el aluminio, el latón, el cobre, el acero dulce, el níquel y el bronce fosforoso, es necesario ajustar el peso calculado multiplicándolo por factores específicos para cada material. Por ejemplo, el peso del aluminio se ajusta multiplicándolo por 0,364, y el del latón por 1,094.
Además, el tipo de malla puede afectar al cálculo. En el caso de una malla de agujeros cuadrados, el cálculo es sencillo si se utiliza la fórmula anterior. Para las mallas de agujeros rectangulares, hay que tener en cuenta el número de mallas de urdimbre y trama y el diámetro de los alambres.
A modo de ejemplo, si se calcula que el peso de una malla de acero inoxidable es de 17,28 kg, en el caso del aluminio sería:
17,28 kg x 0,364=6,29 kg
En resumen, aunque la fórmula básica para calcular el peso de la malla metálica es similar en los distintos materiales, hay que tener en cuenta las densidades específicas de los materiales y los factores de ajuste necesarios. Además, el tipo de malla (agujeros cuadrados o rectangulares) puede influir en el cálculo. Por lo tanto, los ajustes específicos del material y las consideraciones sobre el tipo de malla son esenciales para calcular el peso con precisión.
La influencia del material de una malla metálica en su peso se manifiesta principalmente en la densidad de los distintos materiales. Los materiales de los cables y las mallas metálicas pueden dividirse en alambre de acero, acero al cromo-níquel, acero aleado, acero inoxidable, etc. Estos materiales tienen densidades diferentes, lo que influye en su peso.
Por ejemplo, una malla metálica hecha de alambre de acero, que exhibe una excelente resistencia y durabilidad, es adecuada para soportar tensiones y presiones considerables, y se aplica ampliamente en la industria de la construcción.
Además, los materiales de las mallas protectoras suelen incluir alambre de acero, aleación de aluminio, acero inoxidable, etc. La diferencia de densidad de estos materiales también daría lugar a pesos diferentes. Así pues, puede concluirse que el impacto del material de una malla metálica en su peso se debe principalmente a las diferencias de densidad de los distintos materiales.
La selección del método de cálculo adecuado depende del tipo de malla metálica, como la malla galvanizada, la malla de acero inoxidable, etc. Podemos resumir los siguientes puntos:
Las fórmulas de cálculo del peso de los distintos tipos de mallas metálicas pueden variar. Esto indica que en los cálculos deben tenerse en cuenta las propiedades específicas de las mallas metálicas de distintos materiales.
El cálculo de las piezas de malla metálica puede realizarse mediante un software que calcula automáticamente la longitud en función del material y, a continuación, la multiplica por la anchura especificada en el proyecto. Este método es aplicable a mallas metálicas de diversos materiales, incluidas, entre otras, las mallas metálicas galvanizadas y las mallas metálicas de acero inoxidable.
En términos de soldadura de construcción, el método de cálculo de las especificaciones de las piezas de malla metálica se refleja en la producción de múltiples modelos, tamaños y tipos de estilo. Esto significa que al seleccionar el método de cálculo, es necesario tener en cuenta las especificaciones específicas y los requisitos de aplicación de la malla de alambre.
Para elegir el método de cálculo adecuado, primero hay que conocer el tipo y las características de la malla metálica. En el caso de las mallas metálicas galvanizadas y las mallas metálicas de acero inoxidable, etc., se puede utilizar para el cálculo el método del software que calcula automáticamente la longitud y la multiplica por la anchura. Esto garantiza la precisión y aplicabilidad de los resultados del cálculo.
En aplicaciones reales, la elección del método más adecuado para calcular el peso de una malla metálica requiere considerar primero el tipo específico de malla y su uso. Podemos ver que los distintos tipos de malla tienen fórmulas de cálculo diferentes. Por ejemplo, las fórmulas de cálculo del peso de la malla de cobre y de la malla de acero inoxidable son las siguientes:
Fórmula de cálculo del peso de la malla de cobre Diámetro del alambre × Diámetro del alambre × Número de mallas × Longitud × Anchura ÷ 2 × 1,07 = kg.
Fórmula de cálculo del peso de la malla de acero inoxidable Diámetro del alambre × Diámetro del alambre × Número de mallas × Longitud × Anchura ÷ 2 × 1,07 = kg.
Esto demuestra que los métodos de cálculo para la malla de cobre y la malla de acero inoxidable son similares, siendo la principal diferencia la diferencia de densidad (1,07) causada por los distintos materiales.
Para la malla de chapa de acero y aluminio, su fórmula de cálculo del peso es:
Peso de la malla (kg): Longitud de malla ÷ 1/2 rectángulo de sección corta × Espesor del vástago × Anchura del vástago × Anchura de malla × 7,85.
Esta fórmula incluye varios parámetros, como la longitud de la malla, el rectángulo de sección corta (anchura del orificio), el grosor del vástago, la anchura del vástago y la anchura de la malla, y es adecuada para calcular con precisión superficies mayores o estructuras complejas de mallas metálicas.
Por lo tanto, a la hora de elegir el método de cálculo del peso más adecuado, debe decidirse en función del tipo específico de malla metálica y de su uso. Si se trata de malla de cobre o malla de acero inoxidable, puede utilizarse la fórmula de cálculo general mencionada anteriormente. Para tipos especiales de malla, como la malla de chapa de acero y aluminio, debe utilizarse una fórmula de cálculo diseñada específicamente para ese tipo de malla. Además, las consideraciones de cálculo de costes, como coste:= peso de la malla × precio de la chapa + coste de mano de obra + coste de circulación, también son uno de los factores a tener en cuenta a la hora de elegir un método de cálculo.