Imagine saber exactamente cuánta tensión pueden soportar sus componentes metálicos sin necesidad de cortarlos. La medición de tensiones residuales con rayos X ofrece esta información utilizando métodos de ensayo no destructivos. Este artículo explora cómo las técnicas de difracción de rayos X miden con precisión las tensiones internas, mejorando la fiabilidad y longevidad del producto. Descubra cómo distintos métodos, como las técnicas sin²ψ y cosα, proporcionan datos precisos sobre las tensiones, garantizando que su metalistería cumple los estándares más exigentes. Sumérjase en estas avanzadas técnicas de medición para comprender sus principios, aplicaciones y ventajas para la ingeniería industrial.
La tensión residual es un tipo de tensión interna denominada así en ingeniería. La distribución de la tensión residual en una pieza suele ser desigual, lo que puede afectar significativamente a su resistencia estática, resistencia a la fatiga, estabilidad de forma y resistencia a la corrosión. Por ello, la medición de la tensión residual es crucial.
Existen dos métodos principales para medir tensión residualensayos destructivos y ensayos no destructivos. El método de ensayo destructivo consiste en retirar una parte de la pieza y calcular el tensión residual en función de la deformación y el desplazamiento correspondientes. Entre los métodos de ensayo destructivos más comunes se incluyen los siguientes perforación y el método de núcleo anular.
El método de ensayo no destructivo consiste en establecer una relación entre la tensión residual y una magnitud física que pueda provocar un cambio en el material (como la separación de los planos de cristal, la velocidad de propagación de las ondas ultrasónicas o la permeabilidad magnética) para calcular la tensión residual. Los métodos de ensayo no destructivos incluyen la difracción de rayos X, la difracción de neutrones y los métodos magnéticos y ultrasónicos.
La difracción de rayos X es el método más utilizado para la medición de la tensión residual, debido a la madurez de sus principios y a sus métodos bien establecidos, así como a la disponibilidad de equipos de ensayo cada vez más sofisticados, que incluyen instrumentos de laboratorio, instrumentos portátiles para la medición sobre el terreno y dispositivos especializados para circunstancias especiales.
El método de difracción de rayos X para medir la tensión residual fue propuesto por primera vez por el académico ruso Akchenov en 1929 y equiparaba la deformación macroscópica con la deformación de red. En 1961, el investigador alemán Macherauch desarrolló aún más el método sin2ψ basado en la idea de Akchenov, convirtiendo la medición de la tensión residual por difracción de rayos X en una tecnología fiable y ampliamente utilizada.
En los últimos 60 años, la difracción de rayos X se ha convertido en varios métodos de medición diferentes, con sin2El método ψ y el método cosα son los dos principales métodos utilizados actualmente.
Para dominar la tecnología de difracción de rayos X para medir la tensión residual, es importante comprender sus distintos métodos.
(1) Los métodos de medición de la tensión residual por difracción de rayos X pueden clasificarse en dos enfoques principales: el sin2ψ y el método cosα.
(2) El pecado2El método ψ puede clasificarse, además, en función del método de cálculo de la tensión residual, en el método 2θ, el método del valor d y el método de la deformación.
(3) Basándose en la relación geométrica entre ψ y 2θ, el sin2El método ψ puede dividirse en dos tipos: el método de co-inclinación y el método de balanceo.
(4) El método de medición también puede diferenciarse en función del modo de exploración del tubo de rayos X y del tubo contador, en el método de ψ0 fijo y el método de ψ fijo.
(5) Dentro del método del rollo, existen tres subcategorías: el método del rollo estándar, el método del rollo modificado y el método de fijación del rollo ψ.
(6) Para determinar el esfuerzo cortante τφ se utiliza el método de medición ψ positivo y negativo.
(7) La difracción de rayos X se utiliza normalmente para medir la tensión en una dirección específica en un punto concreto, pero también existen métodos para medir la tensión principal en un punto.
(8) El método de oscilación puede dividirse en varias subcategorías: el método de oscilación ψ0, el método de oscilación ψ, el método de oscilación de anillo de Debye, el método de oscilación de ángulo φ y el método de traslación alterna X/Y.
(9) En cuanto a la geometría de difracción, existen tres enfoques: el método de enfoque, el método de cuasi-enfoque y el método de haces paralelos.
La tensión viene determinada por la deformación. En el caso de los materiales policristalinos, la tensión residual se estima mediante el resultado estadístico de la deformación de la red en la región correspondiente.
Así, la tensión residual puede determinarse midiendo la deformación de la red mediante la técnica de difracción de rayos X.
La tensión residual del material refleja la macrodeformación.
La macrodeformación equivale a la deformación de la red.
La deformación de la red representa el cambio relativo en la separación de los planos cristalinos, que puede calcularse utilizando un dispositivo de difracción basado en la ley de Bragg.
Aquí se resume el método de difracción de rayos X para medir la tensión residual.
Cuando se expone un policristal a un haz de rayos X con una longitud de onda específica (λ), la intensidad máxima de los rayos X reflejados (es decir, el pico de difracción) se observará en un ángulo de difracción específico (2θ), como se ilustra en la figura 1. Este fenómeno se conoce como difracción de rayos X.
La relación entre la longitud de onda de los rayos X (λ), la separación del plano cristalino (d) y el ángulo de Bragg (θ) se describe mediante la siguiente ecuación (1).

En el análisis por difracción de rayos X de la tensión residual, se selecciona el material objetivo adecuado para el tubo de rayos X con el fin de determinar la longitud de onda (λ) adecuada. A continuación, se mide el ángulo de difracción (2θ) con un dispositivo de difracción. Basándose en la medición, se puede calcular la distancia entre planos de cristal (d) del plano de cristal correspondiente.

Fig. 1 Geometría de difracción de rayos X
Según la ley de reflexión de la óptica, la normal del plano cristalino que interviene en la difracción debe situarse en la bisectriz entre los rayos entrantes y reflejados, como se ilustra en la figura 2.
El ángulo entre la normal del plano del cristal de difracción y la normal de la superficie de la muestra se conoce como ángulo acimutal de la normal del plano del cristal de difracción, que suele representarse por ψ.

Fig. 2 Diagrama esquemático de la difracción de rayos X Plano de cristal Acimut ψ
La ley de Bragg permite determinar la separación (dψ) de planos cristalinos en una orientación determinada (ψ).
Si se conoce la separación (d0) de los planos cristalinos en el estado libre de tensiones, se puede calcular la deformación de la red (εψ) en la orientación designada.
S1, S2 y S3 son los ejes de la superficie de la probeta y S1 está definido por el investigador.
La figura 3 ilustra el sistema de coordenadas utilizado para medir la tensión residual mediante difracción de rayos X.

Fig. 3 Sistema de coordenadas para la medición de tensiones por difracción de rayos X
Según la ley de Hooke generalizada, las deformaciones de estos planos cristalinos están influidas por el tensor de tensiones en el punto O y están estrechamente relacionadas con el seno y el coseno de φ y ψ, el módulo de Young del material y la relación de Poisson.
Por lo tanto, es posible determinar la tensión tridimensional en el punto O, incluyendo la tensión (σφ).
La expresión de la deformación en la dirección OP puede deducirse de la teoría de la elasticidad.
Para la mayoría de los materiales y componentes, la profundidad de penetración de los rayos X es sólo de unas pocas micras a decenas de micras, por lo que comúnmente se asume que σ33=0.
Por lo tanto, la deformación en la dirección OP se representa mediante la ecuación (2).


El pecado2La fórmula del método ψ se deriva a partir de la ley de bragg y la teoría elástica.
Los objetos considerados en la teoría de la elasticidad se suponen medios homogéneos, continuos e isótropos.
Sin embargo, esta suposición sólo es válida para los policristalinos materiales metálicos si el tamaño del grano es fino y no hay textura presente.
La Fig. 4 muestra la curva de relación funcional de εn y el pecado2ψ para materiales isótropos, materiales con gradiente de tensión o gradiente de composición, materiales con tensión de cizallamiento y materiales anisótropos con textura.

Como se muestra en la Fig. 4c), si el esfuerzo cortante τ13≠ 0, τ23≠0 y sin2ψ curva tienen ± ψ bifurcación, σφ y τφ puede obtenerse utilizando los datos de deformación medidos ε﹢ψ y ε-ψ en una serie de ángulos ± ψ, como se muestra en la Fórmula (4) y la Fórmula (5).

Es importante señalar que el pecado2ψ mostrada en la Figura 4c) es poco probable que tenga una bifurcación ±ψ.
Esto se debe a que los rayos X utilizados para la difracción tienen una profundidad de penetración limitada en el material analizado, normalmente sólo de unas pocas micras a decenas de micras.
Por consiguiente, las componentes de tensión perpendiculares a la superficie del material pueden considerarse nulas.
Sólo cuando el plano de tensiones principales se desvía de la superficie de la probeta bajo la condición de un mecanizado especial (como un rectificado potente y de gran cantidad de corte) puede τ13≠0 y τ23≠0 ocurrir.
La bifurcación ±ψ no es frecuente, y la curva de ajuste carece a menudo del atributo de elipse. Esto se debe en gran medida al error sistemático del mecanismo ±ψ del goniómetro. Por lo tanto, no es necesario insistir demasiado en la importancia del ajuste de la elipse.
En conclusión, el proceso práctico y aplicable para determinar la tensión residual mediante difracción de rayos X consiste en seleccionar unos pocos ángulos ψ (o varios pares de ángulos ±ψ) y medir el ángulo de difracción correspondiente (2θφψ), seguido de un cálculo.
Los estudiosos han desarrollado diversos métodos para organizar la relación geométrica espacial entre el plano ψ y el plano 2θ, determinar la curva de difracción y realizar cálculos.
El ángulo de difracción 2θφψ se mide mediante el dispositivo de difracción de rayos X, y el espaciado del plano cristalino correspondiente se calcula como dφψ según la ley de Bragg, entonces la deformación de la red εφψ puede expresarse mediante el espaciado del plano cristalino, como se muestra en la Fórmula (6).

La deformación real se sustituye directamente en las ecuaciones (3), (4) y (5) para calcular la tensión, que es la expresión del método de la deformación real.
Se adopta el método de la deformación verdadera, y los valores exactos de d0 y θ0 no son necesarios.
En la mayoría de los casos, el método de la deformación real presenta ventajas significativas.
También se pueden utilizar ecuaciones aproximadas para calcular la deformación, como se muestra en las ecuaciones (7) y (8).

La fórmula de cálculo del método 2θ se muestra en la ecuación (9).

Donde, K es la constante de tensión, y su fórmula de cálculo se muestra en la ecuación (10).

Donde: ν es la relación de Poisson del material.
Para algunos materiales, θ0 varía mucho con la composición química, y los resultados tendrán grandes desviaciones si se utiliza la constante de tensión.
El método de deformación verdadera se ha incluido en la norma de la Unión Europea EN 15305-2008 Ensayos no destructivos - Método de ensayo para el análisis de tensiones residuales por difracción de rayos X y GB/T 7704-2017 Ensayos no destructivos Método de medición de tensiones por rayos X.
El medidor de tensión doméstico XL-640 lista el método de deformación verdadera como método de cálculo de tensión por defecto, y se puede seleccionar el método 2θ para el cálculo.
El método coplanar es un método de medición en el que el plano 2θ coincide con el plano ψ (plano de dirección de la tensión), como se muestra en la Fig. 5.

Fig. 5 Diagrama geométrico del mismo método de inclinación
Con el mismo método de inclinación, el ángulo de incidencia de rayos X ψ0 es dominante, mientras que el ángulo ψ se puede calcular, como se muestra en la Ecuación (11) y la Ecuación (12).

En la prueba de tensión de la pieza de trabajo real, cuando el punto de prueba se encuentra en una ranura poco profunda similar, el espacio de prueba del goniómetro es limitado, por lo que el mismo método de inclinación es más adecuado.
El método del rodillo es un método de medición en el que el plano 2θ y el plano ψ (plano de dirección de la tensión) son perpendiculares entre sí, como se muestra en la Fig. 6.

Fig. 6 Diagrama geométrico del método Roll
La característica clave del método Roll (método χ) es su pequeño factor de absorción del pico de difracción, que contribuye a mejorar la precisión de la medición.
Los rangos de 2θ y ψ pueden ampliarse completamente según sea necesario. Para determinados materiales, pueden utilizarse rayos difractivos con posiciones de pico bajas (como picos por debajo de 145°) para la medición de tensiones.
Sin embargo, el plano 2θ y el plano ψ de este método son perpendiculares entre sí, por lo que requieren un espacio tridimensional, lo que dificulta su aplicación a la medición de espacios estrechos.
El producto de un instrumento de tensión de una empresa extranjera emplea un método Roll modificado con detectores dobles, como se muestra en la figura 7. Su disposición geométrica se representa en la figura.

Fig. 7 Diagrama geométrico del método del rodillo modificado
Ya en enero de 1977, Li Jiabao, del Instituto de Metales de la Academia China de Ciencias, propuso este método de ensayo y esta fórmula de cálculo, como se muestra en las ecuaciones (13) y (14).
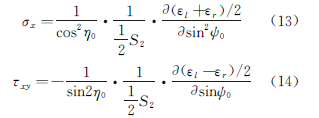
El método del rodillo puede dividirse en dos categorías: el método ψ0 fijo y el método ψ fijo.
El método ψ fijo se considera superior al método ψ0 fijo debido a sus principios más precisos y a sus resultados eficaces en la práctica.
Mediante la combinación de estos dos métodos, el método ψ rollo fijo, el factor de absorción puede ser igual a 1.
Esto significa que el pico de difracción no se inclinará en la parte inferior trasera, la forma del pico seguirá siendo simétrica, y la forma y la intensidad del pico permanecerán sin cambios, incluso si el ángulo ψ cambia, siempre y cuando no haya textura.
Esta característica mejora enormemente la precisión de la medición, lo que convierte al método ψ fijo de rodillo en una técnica de medición ideal.
El método de oscilación consiste en utilizar cada ángulo establecido ψ (o ángulo ψ0) como punto central, y hacer que el tubo de rayos X y el detector oscilen a izquierda y derecha en un ángulo específico (±Δψ o ±Δψ0).
Este método aumenta el número de granos que participan en la difracción, lo que lo convierte en un método eficaz para medir la tensión en materiales de grano grueso.
También pueden utilizarse otros métodos de swing, como el método de swing de ángulo φ y el método de swing de traslación X/Y, e incluso pueden combinarse diferentes métodos de swing para realizar pruebas.
En 2012, PULSTEC, una empresa con sede en Japón, presentó un instrumento de estrés que utiliza por primera vez la tecnología de detectores bidimensionales.
Este instrumento funciona utilizando un único modo incidente y un detector bidimensional para recopilar información de difracción de rayos X, lo que le permite recopilar rápidamente datos del anillo de Debye en el punto de prueba.
Dado que el ángulo ψ formado por la normal de la cara del cristal y la normal de la superficie de la muestra no se encuentra en el mismo plano para cada punto del anillo de Debye, el sin2ψ no puede utilizarse para calcular la tensión. En su lugar, se emplea el método del ángulo α, o cosα (como se muestra en la figura 8).
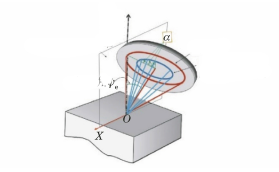
Fig. 8 Diagrama geométrico del método cosα
Este método de ensayo es ideal para medir la tensión superficial en grandes estructuras de acero.
Sin embargo, tiene limitaciones cuando se ensayan materiales de grano grueso o materiales con textura.
El método cosα se basa en los principios de la elasticidad, como demuestran las ecuaciones (15) y (16).

La figura 9 muestra el rango máximo de ángulo ψ que puede adquirirse utilizando un "detector completo de dos posiciones" (con un ángulo de incidencia de 45°).
El ángulo α se encuentra en el plano del anillo de Debye, que es el ángulo central de cada punto del anillo de Debye.

Fig. 9 Localización de los puntos de datos del método sin2ψ en curva s
Ambos métodos para medir la tensión residual mediante difracción de rayos X se basan en el mismo principio mecánico.
El tensor de deformación puede transformarse en el ángulo espacial, y el ángulo α utilizado en el método cosα puede convertirse completamente en el ángulo ψ.
En esencia, el método cosα es esencialmente una aproximación del método sin2Método ψ.
Normalmente, se considera que las chapas de acero laminadas en caliente no tienen textura. Sin embargo, algunas partes chapa de acero pueden presentar textura debido a diversos factores.
A pesar de ello, muchos usuarios siguen optando por utilizar la difracción de rayos X para medir la tensión residual en estos casos.
Por ejemplo, si se selecciona una chapa de acero laminada en caliente con textura, las condiciones de ensayo y los resultados pueden verse en las Tablas 1 y 2. El informe del ensayo para la medición de la tensión residual en el punto Z (0) por cada instrumento se muestra en las figuras 10-13.
Tabla 1 Parámetros de ensayo para medir la tensión residual en caliente Acero laminado Placa con diferentes instrumentos de tensión
| Tipo de equipo | μ-X360S | PROTO LXRD | X-RAYBOT | XL-640 |
| método de ensayo | cosα | sin2ψ | sin2ψ | sin2ψ |
| Tensión/kV | 20 | 30 | 20 | 25 |
| Corriente/mA | 1 | 25 | 1 | 6 |
| Punto iluminado/mm | 1 | 1 | 1 | 1 |
| ψ Gama/(°) | – | -35~35 | -40~40 | 0~45 |
| Método de cálculo de la deformación | – | Método del valor D | Método de deformación | Método de deformación |
| Método de determinación de picos | – | PersonVII | Punto medio | Método de correlación cruzada |
| Tensión residual/MPa | 78 | 213.6 | 144 | 113 |
Tabla 2 Tensión residual de la chapa de acero laminada en caliente medida con diferentes instrumentos de tensión
| Punto de prueba | μ-X360S | PROTO LXRD | X-RAYBOT | XL-640 |
| Z(5) | 29,47 | 122 | 107 | 77 |
| Z(4) | 37,52 | 135 | 112 | 70 |
| Z(3) | 74,70 | 104 | 95 | 67 |
| Z(2) | 38,28 | 153 | 99 | 134 |
| Z(1) | 37,64 | 166 | 122 | 101 |
| Z(0) | 64,78 | 144 | 213 | 113 |
| Z(-1) | 72,71 | 138 | 97 | 139 |
| Z(-2) | 62,52 | 134 | 83 | 145 |
| Z(-3) | 75,70 | 120 | 93 | 153 |
| Z(-4) | 63,56 | 114 | 80 | 148 |
| Z(-5) | 79,27 | 94 | 93 | 152 |

Fig. 10 Anillo de Debye en el punto Z (0) medido con el medidor de tensiones tipo μ-X360S.

Fig. 11 2θ-sin2Curva ψ de Z (0) medida con el medidor de tensiones PROTO LXRD.

Fig. 12 2θ-sin2ψ Curva del punto de medición Z (0) con el medidor de tensión X-RAYBOT

Fig. 13 ε-sin2ψ-curva de Z (0) medida con el tensiómetro XL-640
La tensión residual medida por el método c es menor que la medida por el método s.
Para el punto de prueba Z (0) se utiliza el tensiómetro. De acuerdo con el principio de igual espaciamiento de sin2ψ, se seleccionan 8 ψ ángulos dentro del rango de 0 °~45 °.
Los resultados se muestran en las figuras 14-15. Se puede observar que el sin2La curva ψ del material presenta un tipo de "choque" debido a la textura.
La ordenada del pecado2ψ curva de la Fig. 13 es la deformación ε. Después de cambiar la ordenada a 2θ, realizar el ajuste lineal. Los resultados se muestran en la Fig. 14.
La pendiente M de la línea de ajuste es de -0,355, y la tensión residual σ es de 113MPa.

Fig. 14 Resultados del ajuste de 2θ-sin2Curva ψ medida por el tensiómetro XL-640 en el punto Z (0)
El rango ψ seleccionado por el medidor de tensión μ-X360S es equivalente a los dos primeros valores 2θ de apantallamiento y, a continuación, se realiza el ajuste rectilíneo. Los resultados se muestran en la Fig. 15.

Fig. 15 Resultados del ajuste de 2θ-sin2Curva ψ de Z (0) medida por el instrumento de tensión tipo μ-X360S.
Utilizar el medidor de tensión PROTO LXRD para probar el rango ψ seleccionado, blindar los tres últimos valores 2θ en la Fig. 14, y luego realizar el ajuste lineal. Los resultados se muestran en la Fig.16.

Fig. 16 Resultados del ajuste de 2θ-sin2Curva ψ medida por el medidor de tensiones PROTO LXRD en el punto Z (0)
En la figura 12 se observa que el máximo sin2El valor ψ del punto Z (0) es 0,4 utilizando el medidor de tensión X-RAYBOT.
De acuerdo con el rango ψ seleccionado, apantallar los dos últimos valores 2θ de la Fig. 14 y, a continuación, realizar el ajuste lineal. Los resultados se muestran en la Fig. 17.

Fig. 17 Resultados del ajuste de 2θ-sin2ψ Curva de Z (0) medida por el medidor de tensiones X-RAYBOT
Debido a la textura del material, su sin2La curva ψ es oscilatoria.
El intervalo de ángulos ψ seleccionado es diferente, lo que da lugar a diferencias en la pendiente y los valores de tensión residual obtenidos a partir de la línea de ajuste.
En el caso de materiales de textura desconocida y grano grueso, no es aconsejable elegir un rango de ψ estrecho y un número reducido de estaciones de ψ para la medición de la tensión residual, ya que esto puede dar lugar a errores de medición significativos.
El ajuste lineal puede no ser apropiado para materiales con textura sin2ψ curvas oscilantes.
Durante el proceso de medición, a menudo se utiliza el ajuste lineal para mitigar las fluctuaciones causadas por las vibraciones y los errores de medición.
Puede que no sea factible alcanzar un ángulo ψ de 45°, ya que podría verse influido por la profundidad de penetración. Es más probable que un ángulo mayor produzca resultados más precisos, siempre que pueda ignorarse la profundidad de penetración.
En el caso de materiales con grano grueso o textura, el intervalo de ángulos ψ debe ampliarse todo lo posible para eliminar los efectos de la no linealidad ε-sin2ψ. Esto puede lograrse midiendo ambos ángulos ±ψ.
La precisión de las rectas ajustadas puede mejorarse utilizando el método de los mínimos cuadrados para ajustar la regresión y aumentando tanto el intervalo ψ como el número de estaciones ψ. De este modo se obtendrán valores de prueba más fiables.
La precisión de la medición también puede mejorarse aumentando el área de exposición a los rayos X o aumentando el número de granos de difracción que participan mediante el método de oscilación.
(1) El pecado2El método de ψ puede utilizarse para determinar la tensión residual con mayor precisión aumentando el rango de ψ y seleccionando más estaciones de ψ. Sin embargo, este método tiene limitaciones, ya que implica una sola exposición, lo que puede dar lugar a grandes errores de medición si el rango de ψ no es suficiente.
(2) En los métodos de medición que utilizan el sin2ψ principio, el método del balanceo es superior al método de la inclinación. Se recomienda utilizar el método del balanceo siempre que las condiciones de espacio en el punto de medición lo permitan. Para medir la tensión residual en las ranuras de determinados componentes, se suele utilizar el método de co-inclinación.
(3) El método de la deformación verdadera es el preferido para calcular la tensión residual.
(4) El método sin2ψ se considera un método estándar para este fin. Para obtener los resultados más precisos, el ángulo ψ debe fijarse utilizando el método sin2Método de bisección del valor ψ y deben medirse tantos ángulos ψ como sea posible.