¿Y si pudiera perfeccionar los intrincados doblados en forma de Z en metal con precisión y facilidad? Este artículo profundiza en los matices estructurales del plegado en forma de Z y la matriz de conformado, destacando técnicas y cálculos esenciales. Descubrirá cómo optimizar los procesos de plegado, comprender la distribución de tensiones y utilizar matrices compuestas para diversos materiales de chapa. Tanto si es ingeniero como maquinista, obtendrá información que agilizará la producción y mejorará la precisión en sus proyectos metalúrgicos. Sumérjase para dominar las complejidades del plegado en forma de Z y mejorar su flujo de trabajo.
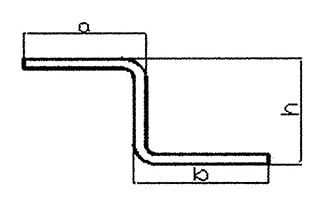
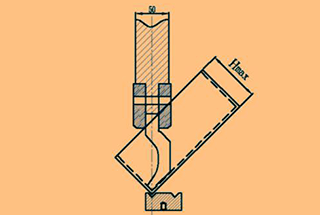
La pieza curvada en forma de Z que se muestra en la figura 1 es una pieza que suele encontrarse en la producción. El tamaño de h está limitado por la matriz inferior, y el tamaño mínimo que puede doblar la matriz inferior existente se muestra en la Tabla 1.
Cuadro 1 Tamaño mínimo de flexión
| Espesor de la placa | 1 | 1.5 | 2 | 2.5 | 3 |
| Tamaño mínimo | 7 | 9.5 | 14 | 16 | 18 |
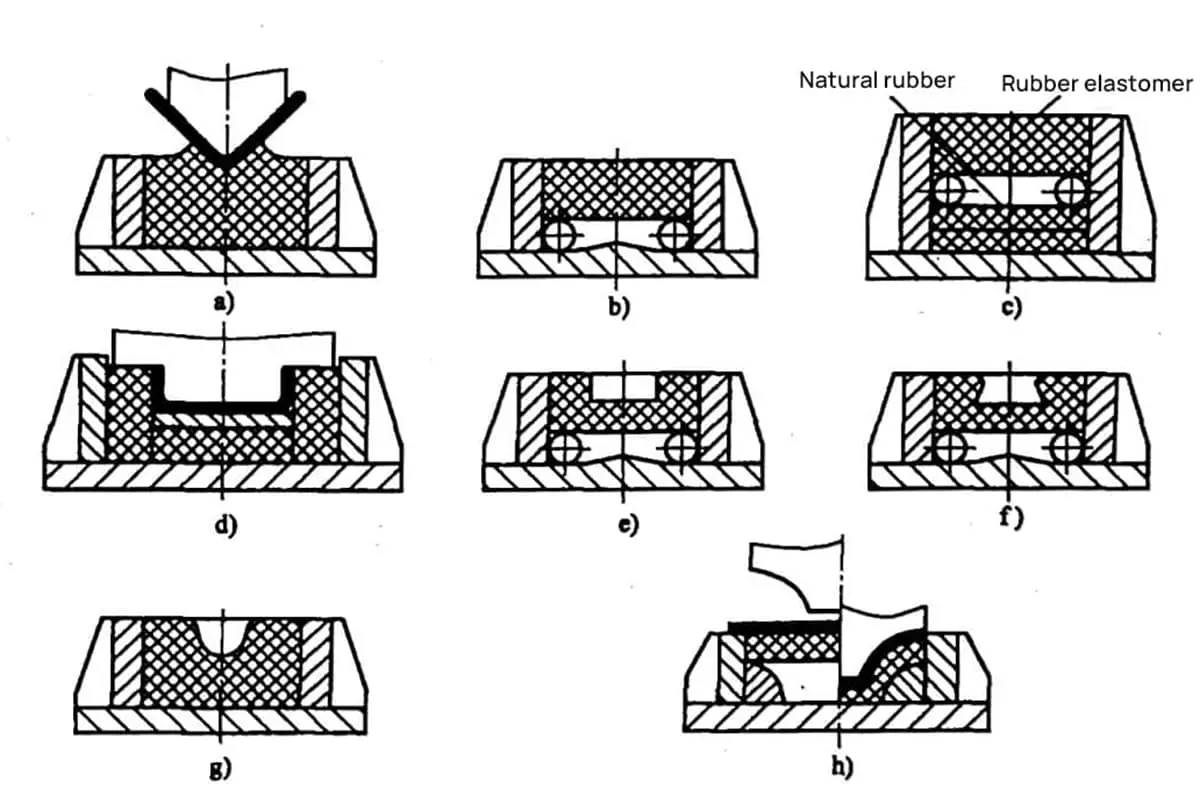
En la producción práctica, si hay numerosos troqueles de doblado en forma de Z que son más pequeños que el tamaño mencionado, se requeriría el diseño de un troquel de doblado compuesto para lograr el moldeo primario. Este troquel compuesto puede utilizarse para plegar troqueles de plegado en forma de Z de varios tamaños en diferentes materiales de lámina.
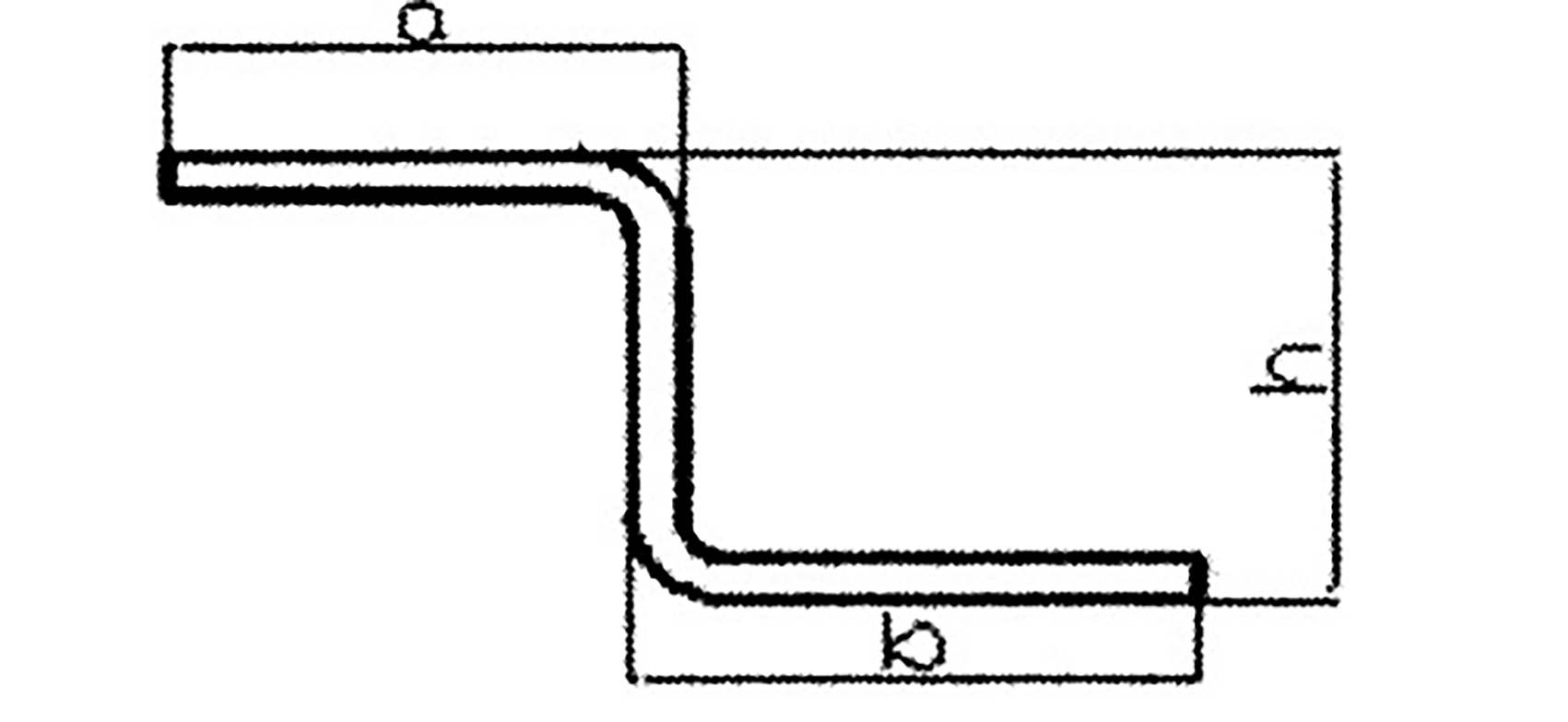
Fig. 1 En forma de Z matriz dobladora
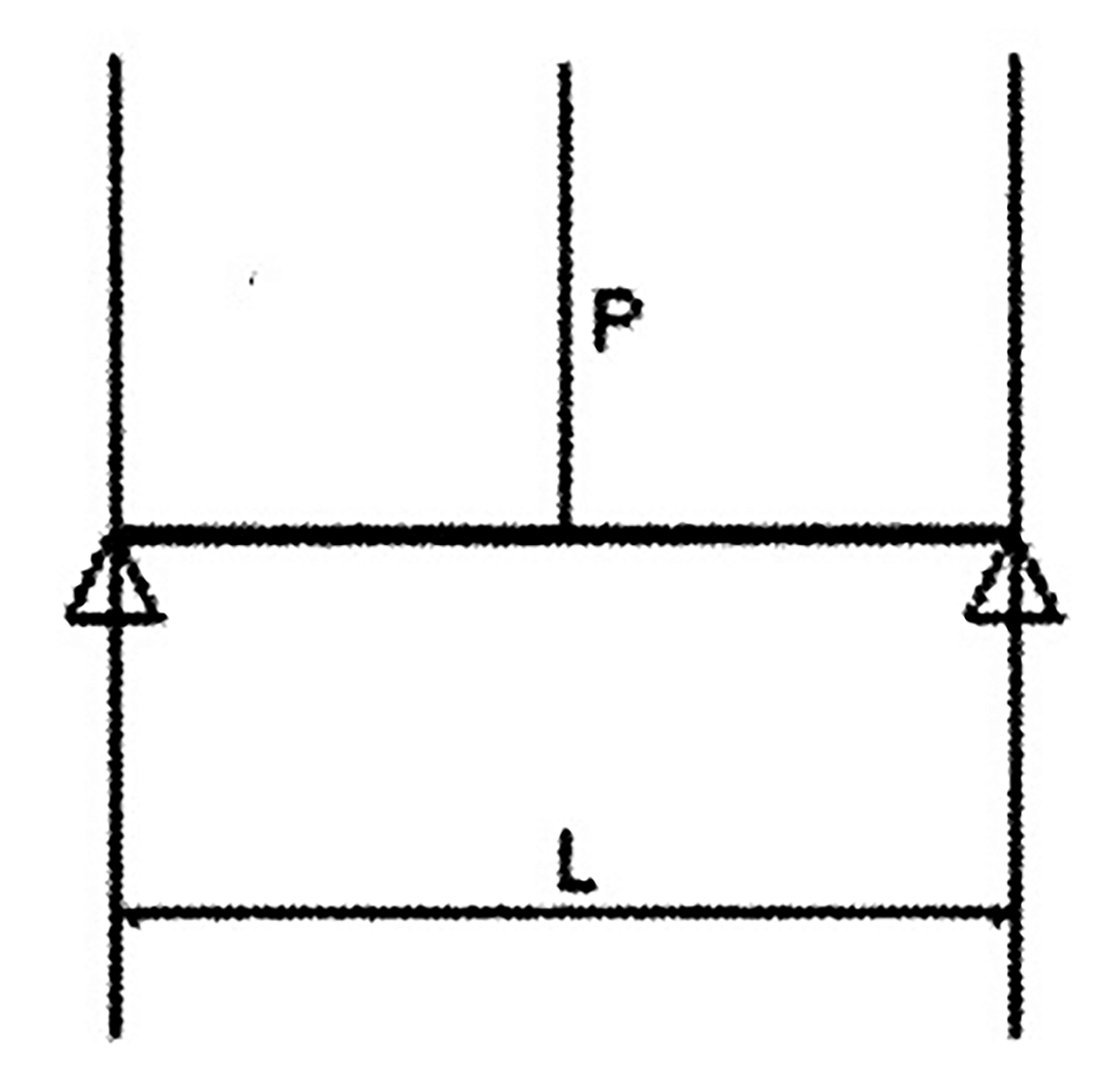
Fig. 2 Diagrama de fuerzas de acción
Como se muestra en la figura 2, cuando un chapa metálica está sometido a flexión, experimenta momento flector, fuerza cortante y presión local. Sin embargo, el principal efecto de la deformación por flexión es el momento flector.
La aplicación de una fuerza externa provoca la correspondiente deformación de la chapa, lo que también desencadena la aparición de una fuerza interna que resiste la deformación. La fuerza interna se equilibra con la fuerza externa y se mide como tensión, que es la fuerza interna por unidad de superficie del objeto. Cuanto mayor sea la fuerza externa, mayor será la tensión y la deformación.
Cuando la tensión exterior del material es inferior a su límite elástico, la chapa se encuentra en estado de deformación elástica. Según la ley de Hooke, la relación lineal entre la tensión y la deformación en la sección se debe al cambio lineal de la distancia entre la deformación y la capa central (alargamiento de la capa exterior y acortamiento de la capa interior).
Si se elimina la fuerza externa, la chapa recupera su forma original. Sin embargo, si la fuerza externa sigue aumentando, el grado de deformación de la pieza de flexión seguirá escalando hasta que la tensión causada por la fuerza externa iguale el límite de elasticidad del material, lo que provocará la deformación plástica del material exterior.
A medida que aumenta la fuerza externa, la deformación plástica progresa desde la superficie hacia el centro. Una vez eliminada la fuerza externa, la deformación elástica desaparece inmediatamente, pero la deformación plástica permanece y da lugar a una deformación permanente por flexión.
Si la tensión provocada por la fuerza externa supera el límite de resistencia del material, la chapa sufre una fractura por deformación plástica. Compresión interna durante plegado de chapa también produce deformación plástica, pero este tipo de deformación plástica aumenta la tensión en la superficie sin causar daños, por lo que a menudo se ignora.
Ahora observamos detenidamente la deformación plástica por flexión.
Bajo la acción del momento flector, existen tres líneas iguales en la sección de la placa: ab= a1b1 = a2b2.
Tras la flexión, la capa interior se acorta y la exterior se alarga, es decir, ab < a1b1 < a2b2.
Por lo tanto, durante la flexión, el material interior se somete a compresión y se acorta, mientras que el material exterior se estira y se alarga.
Entre la tensión y la compresión hay una capa de material que no experimenta ni estiramiento ni compresión y que se denomina capa neutra. Esta capa no cambia de longitud y no se alarga ni se acorta.
El proceso de cálculo de la pieza de flexión implica dividirla en varios elementos geométricos básicos, incluidos segmentos de línea recta y segmentos de arco. La longitud de cada elemento se calcula individualmente, y la longitud total de todos los elementos es la longitud desplegada de la pieza de flexión.
La pieza de flexión en forma de Z de la figura 1 puede dividirse en cinco unidades, como muestra la figura 2. Las unidades 1, 3 y 5 son segmentos de línea recta, mientras que las unidades 2 y 4 son segmentos de arco. Las unidades 1, 3 y 5 son segmentos de línea recta, mientras que las unidades 2 y 4 son segmentos de arco.
Como se ha comentado anteriormente, la capa de fibra con longitud constante en el centro antes y después de la flexión se denomina capa neutra. Cuando se calcula la longitud de expansión del segmento de arco, en realidad se está calculando la longitud de la capa neutra del segmento de arco.
La posición, x, de la capa neutra desde el lado interior del arco (como se muestra en la figura 3) suele estar determinada por la relación r/t.
x = kt
Dónde:
Dónde:
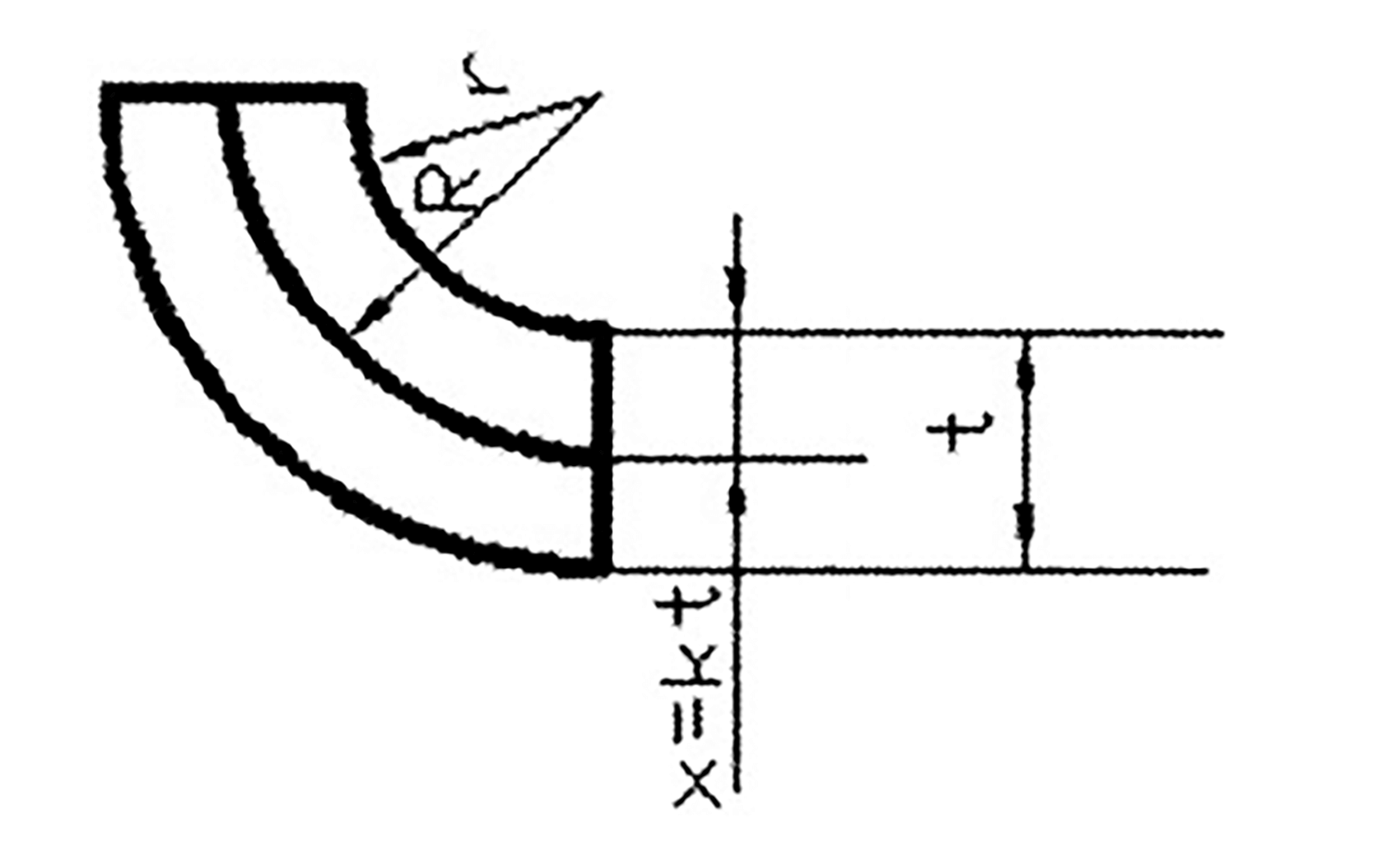
Fig. 3
El valor de k varía en función de la relación entre el radio interior y el espesor de la chapa, como se muestra en la tabla 2:
Cuadro 2
| r/t | 0.25 | 0.5 | 1 | 2 | 3 | 4 |
| k | 0.26 | 0.33 | 0.35 | 0.375 | 0.4 | 0.415 |
En la producción práctica, lo más habitual es doblar chapas de acero para darles una forma de 90 grados.
El cálculo de la longitud de arco para una flexión de 90 grados con diferentes valores de r y t puede obtenerse mediante tablas de referencia en aplicaciones prácticas.
Este artículo se centra en la flexión en ángulo recto de 90 grados, pero no es eficiente calcular los segmentos de línea recta y arco por separado para piezas con 90 grados plegado de chapa. En su lugar, se marcan como se muestra en la Figura 1.
Al calcular el material desplegable, podemos utilizar directamente las dimensiones marcadas para simplificar el proceso de cálculo.
Según la figura 1, se calcula la longitud desarrollada del material:
L = a＋b＋h - 2x
Dónde:
Cuadro 3 Coeficiente de flexión común x
| Espesor de la placa t | Interior radio de curvatura r | |||
|---|---|---|---|---|
| 1.0 | 1.5 | 2.0 | 2.5 | |
| 0.5 | 1.0 | 1.2 | 1.4 | 1.6 |
| 1 | 1.9 | 2.1 | 2.3 | 2.5 |
| 1.5 | 2.5 | 2.7 | 2.9 | 3.1 |
| 2.0 | 3.4 | 3.6 | 3.8 | 4.0 |
| 2.5 | 4.0 | 4.2 | 4.4 | 4.6 |
| 3 | 4.9 | 5.1 | 5.3 | 5.4 |
Este troquel de ajuste simple es distinto del troquel convencional.
Está diseñada para ser sencilla, rápida, fácil de procesar y sencilla de conformar. Aunque puede no ser tan preciso como el troquel convencional, se sigue utilizando para procesar productos con rapidez y precisión.
El diagrama de conformado de la matriz compuesta se muestra en la Tabla 3.
Principio de procesamiento: El grosor de la junta se ajusta para conseguir la anchura deseada de la ranura en V en la parte superior e troquel inferiory realizar un único procesamiento de pliegue en Z bajo presión.
Estructura de la matriz: La matriz de doblado en forma de Z consta de una matriz superior, una inferior, una junta y un prisma angular de acero.
Espesor de la junta: El espaciador está hecho de 0.5 mm de grosor de acero y se apila para alcanzar el grosor requerido.
Prisma de acero: Una pieza de acero rectangular dentro de la matriz, sus cuatro ángulos están achaflanados en lados de 0,5 mm, 1,0 mm, 2,0 mm y 4,0 mm, como se muestra en la Tabla 3.
El troquel simple especial se utiliza para conseguir la anchura deseada de la ranura en V de los troqueles superior e inferior ajustando el tamaño del acero del prisma angular y el grosor de la junta, y realizando a continuación el proceso de plegado en Z en una sola prensa.
Este método se elige debido a la posibilidad de aumentar la ranura en V y reducir las arrugas, por lo que diferentes espesores de placa requieren diferentes puntas, como se muestra en la Tabla 4.
Cuadro 4
| Espesor de la placa | t<0.8 | 0.8<t<1.0 | 1.0<t<1.2 | 1.2<t1.5 | t＞1.5 |
| Clavija | 0.5 | 1.0 | 1.0 o 2.0 | 2.0 | 4.0 |
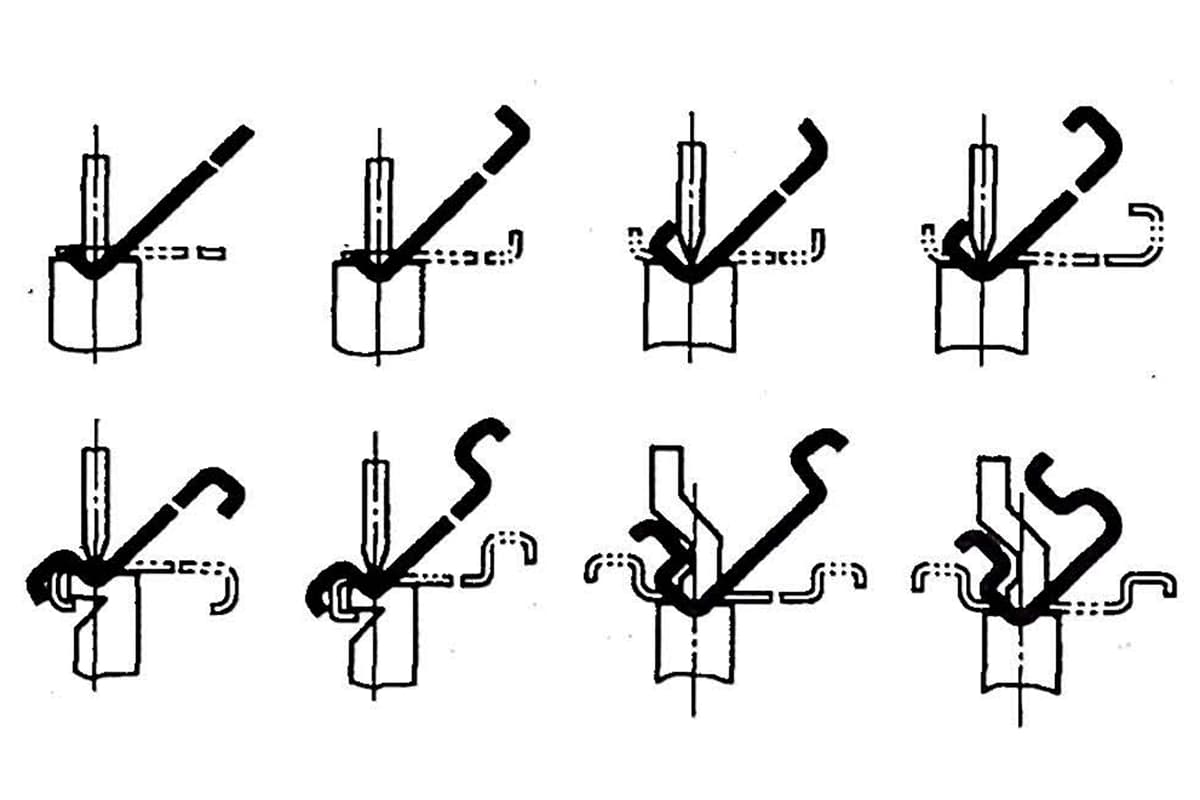
Método de depuración de la matriz de doblado en forma de Z:
1) Los dos pliegues del pliegue en Z de la regla son de 90°. La distancia entre las dos puntas de la herramienta es 1.414/2×h;
2) Si el pliegue de la pieza es demasiado profundo, es necesario elegir un ángulo grande.
b: almohadilla de hierro; c: aumentar el ángulo R;
3) Si se alcanza la altura, pero el ángulo es superior a 90°, entonces a: excentricidad del troquel.
b: Aumentar el grosor de la cuña;
4) Si los dos lados del pliegue en Z no son paralelos, puede conseguirse aumentando o disminuyendo el grosor de la cuña.
Si el pliegue superior es superior a 90°, es necesario aumentar el grosor de la cuña inferior de la matriz; y si el pliegue inferior es superior a 90°, es necesario aumentar el grosor de la cuña superior de la matriz.
Método de cálculo de la dilatación en Z:
Cuando h > tamaño normal de flexión, debe desplegarse en dos pliegues.
L=a + b + h - 2x
Dónde:
Cuando h < el tamaño normal de flexión, se expande mediante conformado en un paso.
L = a + B + h - 1,5x
Dónde:
Una de las fórmulas empíricas en la práctica consiste en restar 1,5x a la dimensión total de una moldura.
Como fundador de MachineMFG, he dedicado más de una década de mi carrera a la industria metalúrgica. Mi amplia experiencia me ha permitido convertirme en un experto en los campos de la fabricación de chapa metálica, mecanizado, ingeniería mecánica y máquinas herramienta para metales. Estoy constantemente pensando, leyendo y escribiendo sobre estos temas, esforzándome constantemente por mantenerme a la vanguardia de mi campo. Deje que mis conocimientos y experiencia sean un activo para su empresa.
ES 
EN 
AR 
DE 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO