6 Factors Affecting the Bending Radius of Sheet Metal

Looking to bend sheet metal? Understanding the factors that impact the bending radius is crucial to achieving the perfect bend.

From the thickness of the metal to the material it’s made of, the radius of the top punch, the bottom die, the bending force applied, and the working temperature, there are numerous variables to consider.

In this article from MachineMfg, we break down the key factors that affect the bending radius of sheet metal.

You’ll learn how to choose the optimum bending radius, what factors can impact it, and how to adjust your bending allowance table for different materials.

Plus, we’ll cover the importance of the top punch radius, bending force, and bottom die width in determining the bending radius.

Whether you’re a seasoned metalworker or just starting out, this guide will help you achieve the perfect bend every time.

So, grab your sheet metal and get ready to dive into the world of bending radius!

Optimum Bending radius

There should have a bending radius for sheet metal bending, it should not be too large or too small, and should be chosen appropriately.

If the bending radius is too small, it will cause cracking at the bend position;

If the bending radius is too large, it is easy to rebound.

However, you can use V grooving machine to groove first, and then bend. In this way, you will get a smaller bending radius.

The optimum bending radius of different thicknesses of various materials (bend inner RADIUS) see table below:

The data in the table above is the preferred data for reference only. In fact, the rounded corners of press brake are usually 0.3, and a small number of the rounded corners of the press brake punch is 0.5.

For ordinary low carbon steel plate, anti-rust aluminum plate, yellow copper, purple copper etc, the inner radius 0.2 is no problem, but for some high carbon steel, hard aluminum, super-hard aluminum, the use of 0.2 radius will lead to bending fracture or the outer radius crack.

Factors that may affect the bending radius

What are the factors that may affect the bending radius of the sheet metal?

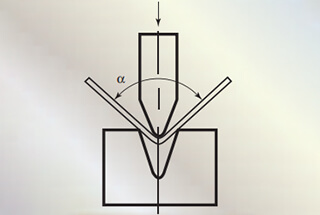
There are several factors that can impact the bending radius of sheet metal, including the thickness of the metal, the material it is made of, the radius of the top punch, the bottom die, the bending force applied, and the working temperature.

I hope this article, based on my personal experience, will be helpful to readers.

Bending Angle

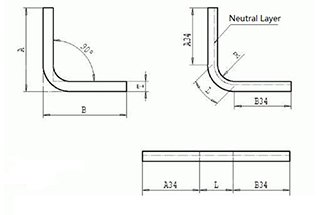
The bending angle of the sheet metal is the key factor affecting the bending allowance.

For example, if bending the sheet metal with large radius, more bending allowance will be deducted; if bending acute angle, less bending allowance shall be deducted.

Sheet Metal Thickness

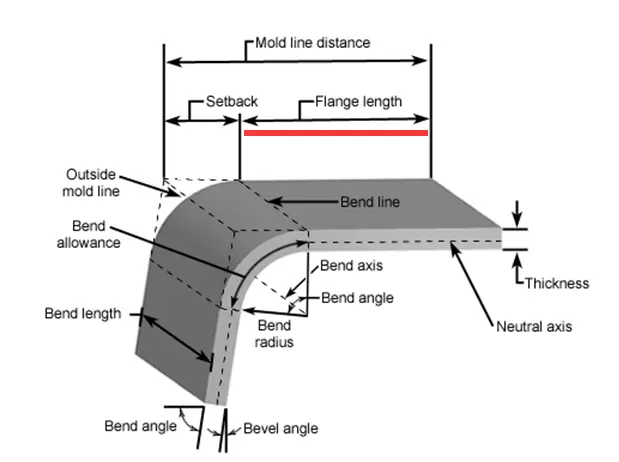
In practical applications, it has been observed that the bend radius increases as the material thickness increases.

We are aware that a thicker plate requires more bending force and a larger vee opening in the lower die.

What then affects the bend angle r?

Sheet Metal Material

The bending allowance for sheets of the same thickness can vary slightly, demonstrating that material properties play a role in determining the bending radius.

The material’s resistance to bending can directly influence the bending radius.

Although the material has an impact on the bending radius, it has limited effect on our actual usage.

We can create a custom bending allowance table for different materials.

Punch Tip Radius

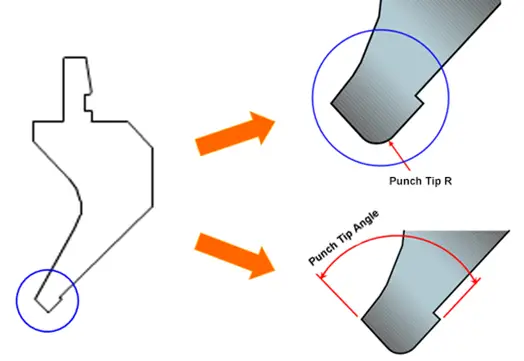
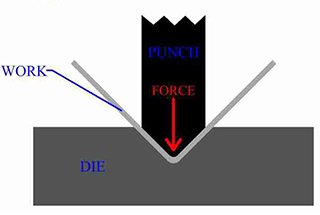
The standard bending mold radius must not exceed r1, and the minimum radius of the punch must be no less than 1.

If there are no specific requirements for the bending radius, it will have limited impact on the bending process.

However, for sheet metal bending that requires a specific bending radius that is either less than 1 or significantly larger than 1, it is not solely determined by the radius of the top punch.

Therefore, the radius of the top punch directly affects the final bending radius.

It is important to bear in mind that where the radius of the punch tip is greater than the radius generated by the vee die used in the bending, it will affect the internal radius of the profile.

For example:

• 1 mm mild steel to be bent
• Die chosen V = 8 mm, which, as shown below, produces a 1mm internal bending radius.

The internal bending radius will be:

• r= 1 mm, where the punch tip radius is less than Imm
• or r = punch tip radius where the punch tip radius is greater than 1mm.

A typical example of this principle is represented by radius tool holders that can be used to obtain large-radius bends in small dies. In this case, the required internal radius is produced by the shape of the punch tip.

Where instead you wish to retinthe internal bend radius produced by the
die, the ideal punch tip rdius can be calculaled with the following equation:

Ideal punch tip radius = (R produced by the die) x (2/3)

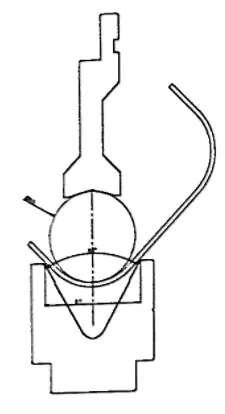
Using this ratio the punch surface is proportional to the required force to bend the sheet metal prevening the punch tip from penetrating the sheet metal. This avoids aesthetic problems or cracks in the material on the inside of the bend.

In addition, with a tip radius that is too small and with acute angles it is possible for the metal sheet to be almost cut through and for the profile to close onto the punch thus producing an angle different from the one intended.

It is not always easy to comply with the above-mentioned equation due to a lack of different bending tip radi in many workshops.

However, press brake operators should use the tip radius closest to the ideal. Especially for thick sheet metal, which requires high force to be bent, operators must use appropriate punch tip radi to avoid sheet metal deformations, dimensional problems or problems involving appearance or cracking.

Bending Force

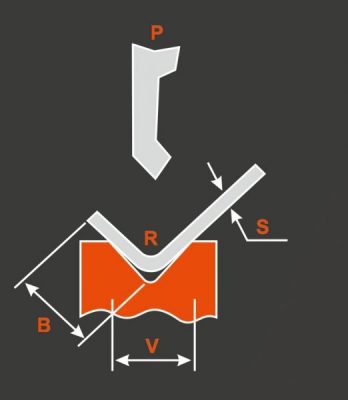
The thicker the sheet metal, the more resistance it has to bending deformation.

Therefore, the bending force must be adjusted accordingly.

The bending force cannot be constantly increased and must be set to an appropriate level.

The bending force is directly proportional to the thickness of the sheet metal and inversely proportional to the width of the lower die slot.

When bending, the thickness of the sheet metal is fixed and the width of the lower die slot is selected based on the thickness of the metal.

As a result, the bending force becomes a constant, determined by other factors.

The bending radius cannot be accurately determined without considering the bending force.

Bottom Die

The width of the lower die slot has a direct correlation with the thickness of the sheet metal.

In real-world applications, the bend radius increases as the thickness of the metal increases.

For the same thickness of sheet metal, the bending radius can also vary depending on the width of the vee opening.

Therefore, it is clear that the width of the lower die slot plays a crucial role in determining the bending radius.

Operating Temperature

Generally, the working environment temperature is room temperature, which can be ignored.

Conclusion

The bending force contributes to changes in the bending radius, but it is determined by the thickness of the sheet metal and the width of the lower die slot.

All factors play a role in determining the bending radius, and they can only be limited based on specific requirements.

For example, if there are no specific requirements for the bend radius, limiting all factors and using a standardized bending factor table is appropriate.

If a much larger bend radius than 1 is desired, the radius of the upper die can be modified and a customized bending factor can be used.

However, it is not advisable to alter the width of the lower die slot, as it will have an impact on both the bending radius and the bending allowance.

Modifying the width of the lower die slot can be used to change the bending allowance and bending radius.