What makes a material bend without breaking? The elastic modulus is key, influencing how materials respond under stress. This article explores five critical factors affecting the elastic modulus: alloy elements, heat treatment, strain hardening, cold plastic deformation, and temperature. Readers will gain insights into how these variables impact material properties, essential for engineering applications.
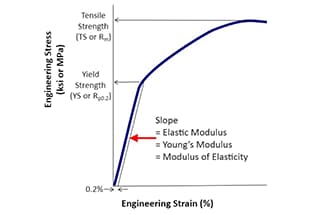
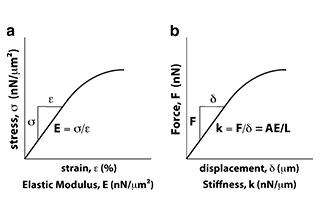
The elastic modulus of steel is primarily determined by the intrinsic properties of the metal atoms and the crystal lattice structure. This fundamental relationship arises from the interatomic forces, which are largely dependent on the electronic structure of the metal atoms and their spatial arrangement within the lattice.
While alloying elements can induce changes in the lattice parameters of steel, their impact on the elastic modulus is generally minimal for most conventional steel alloys. This limited effect is due to the relatively small alterations in interatomic spacing and bonding that occur with typical alloying additions. Consequently, the elastic modulus values of alloy steels and carbon steels tend to be quite similar.
Quantitatively, the variation in elastic modulus between alloy steels and carbon steels is typically less than 12%. This relatively small difference underscores the dominance of iron’s inherent properties in determining the elastic behavior of steel, even when alloyed with significant quantities of other elements.
It’s worth noting that while the elastic modulus remains relatively constant, alloying elements can significantly influence other mechanical properties such as yield strength, tensile strength, and ductility through various strengthening mechanisms (e.g., solid solution strengthening, precipitation hardening, or grain refinement).
Heat treatment generally exerts minimal influence on the elastic modulus of metals. This is evidenced by several key observations:
However, the relationship between heat treatment and elastic properties becomes more complex when considering specific alloys and mechanical properties:
It’s important to note that while this behavior is observed in 60Si2MnA, the universality of this relationship across different alloys and heat treatment processes requires further investigation. Engineers and materials scientists should consider these potential variations when designing components or structures that rely on precise elastic and shear properties, especially for high-performance applications such as springs or precision instruments.
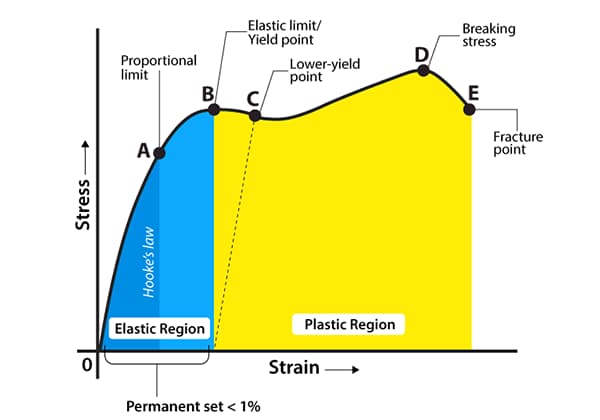
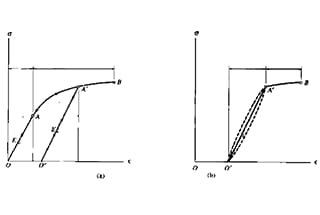
If the test piece is a plastic material, which is loaded to the plastic stage and then unloaded, when the material returns to the equilibrium state, the elastic strain will disappear, while the plastic strain will not disappear, resulting in permanent deformation of the material, as shown in Fig. a.
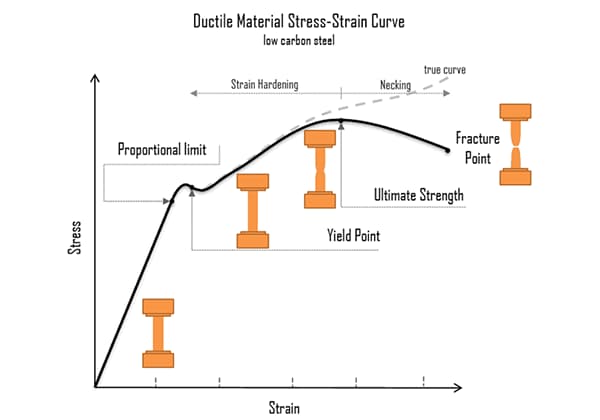
This process is called strain hardening or cold work hardening.
Thus, although the proportional limit is increased, the plasticity is reduced to a certain extent and the brittleness is increased.
It can be seen from figure a that before and after strengthening, the straight line of the linear section of the curve tends to be parallel, the slope is the same, and the elastic modulus is the same.
In fact, the specimen will lose some heat or energy when unloaded from point a ‘and then loaded to the same point.
Therefore, the curves of loading and unloading process do not coincide.
As shown by the dotted line in Fig. b, there will be a mechanical hysteresis zone.
When selecting damper materials for vibrating structures or mechanical equipment, the mechanical hysteretic characteristics should be taken into account.
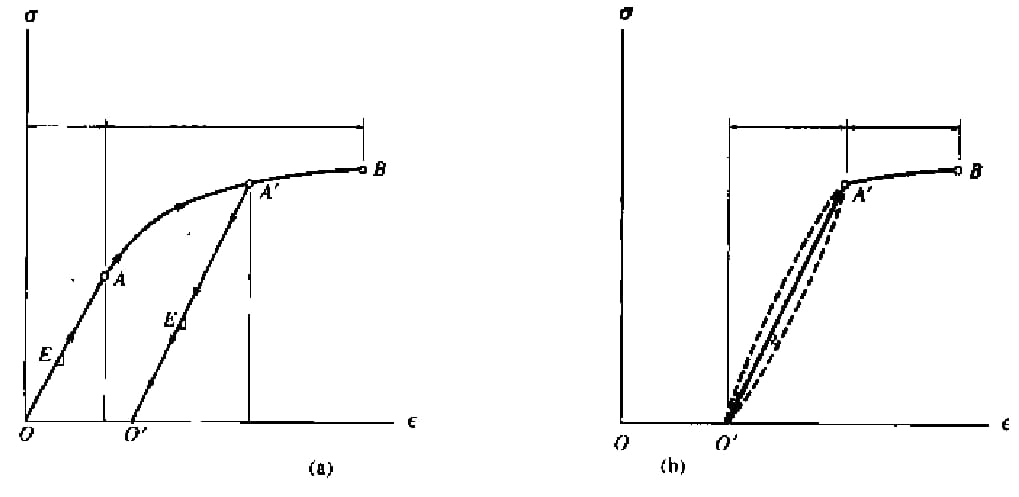
Schematic diagram of material strengthening process
Cold plastic deformation induces a slight reduction in the elastic modulus of metals, typically ranging from 4% to 6%. This phenomenon is primarily attributed to the development of residual stresses within the material’s microstructure during the deformation process.
The magnitude of plastic deformation significantly influences the anisotropy of the elastic modulus. As the degree of deformation increases, the material exhibits directional dependence in its elastic properties. Notably, the elastic modulus reaches its maximum value along the primary direction of deformation, a consequence of crystallographic texture evolution and dislocation substructure formation.
This alteration in the elastic modulus due to cold plastic deformation has important implications for the cold forming of precision components. The induced anisotropy and overall reduction in elastic modulus can lead to:
To mitigate these effects and achieve high-precision cold forming, manufacturers must consider:
As temperature increases, the interatomic distances within the material’s crystal structure expand, leading to a reduction in the elastic modulus. This temperature-dependent behavior is crucial in engineering applications, particularly in high-temperature environments.
For carbon steel, a significant material in industrial applications, the elastic modulus exhibits a notable temperature sensitivity. Specifically, for every 100°C increase in temperature, the elastic modulus of carbon steel decreases by approximately 3% to 5%. This reduction is attributed to the weakening of interatomic bonds and increased atomic vibrations at higher temperatures.
However, it’s important to note that within the temperature range of -50°C to 50°C, which encompasses most ambient operating conditions, the elastic modulus of steel remains relatively stable. This stability in the elastic properties within this range contributes to the predictable and reliable performance of steel structures and components under normal environmental conditions.
The temperature-dependent behavior of the elastic modulus has significant implications for design and material selection in various applications, such as high-temperature processing equipment, aerospace components, and structures subject to extreme temperature variations. Engineers must account for these changes when designing components that will operate across wide temperature ranges to ensure structural integrity and performance throughout the intended service life.
Because elastic deformation propagates in the medium at the speed of sound, the speed of sound in the metal medium is quite large, such as 4982m / s in steel;
In the ordinary pendulum impact test, the absolute deformation rate is only 4 ~ 5.5m/s, and even in the high-speed impact test, the deformation rate is within 103m / s.
Under such impact load, the elastic deformation can always follow the change of external impact force, so the strain rate has no effect on the elastic behavior and elastic modulus of metal materials.
In modern machines, the strain rate of various parts ranges from 10-6 to 106s-1.
For example, the strain rate of static tensile test is 10-5 ~ 10-2s-1 (referred to as quasi-static strain rate), and the strain rate of impact load is 102 ~ 104s-1, referred to as high strain rate.
In addition, there are medium strain rate tests with strain rate of 10-2 ~ 102s-1, such as drop hammer and rotating flywheel.
The practice shows that when the strain rate is in the range of 10-4 ~ 10-2s-1, the mechanical properties of the material have no obvious change and can be treated as static load.
When the strain load rate is greater than 10-2s-1, the mechanical properties of the material will change significantly, which must take into account a series of changes in mechanical properties caused by the increase of strain rate.
In the plastic deformation stage, the deformation increases slowly with the increase of the loading rate.
Therefore, when the loading rate is very fast, the plastic deformation cannot be fully carried out, which is manifested as the improvement of the elastic limit, yield strength and other micro plastic deformation resistance.
It is also found that the plastic deformation under impact load is concentrated in some local areas, which reflects that the plastic deformation is extremely uneven.
This non-uniformity also limits the development of plastic deformation, making the plastic deformation unable to be fully carried out, resulting in the improvement of yield strength and tensile strength, and the improvement of yield strength is more and the improvement of tensile strength is less.
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN
AR
DE
ES
FR
IT
JA
NL
PT
PT_BR
RU
KO